基于偏联系数的得分函数构造方法

王万军，王素华，杜 佳，张成文，2，马少斌，2

(1.兰州文理学院 数字媒体学院，甘肃 兰州 730000；2.兰州文理学院 VR技术研发与推广中心，甘肃 兰州 730000；3.西北民族大学 数学与计算机科学学院，甘肃 兰州 730030；4.西北师范大学 外国语学院，甘肃 兰州 730070)

0 引言

自赵克勤提出集对分析[1](Set Pair Analysis, SPA)以来，SPA理论已经广泛应用于社会、政治、经济、文化、决策及信息处理等领域.集对分析是定义在[0,1]区间上的具有同(肯定/确定)、异(犹豫/不确定)、反(对立/否定)特性，采用联系数函数刻画事物规律的集合对.集对分析联系数(度)函数克服了Fuzzy集[2]中隶属度函数描述模糊信息的单一缺陷，弥补了Vague集[3]中隶属度和非隶属度对信息犹豫不确定性无法描述的不足，改进了Intuitionistic集[4]中真(肯定)隶属函数和假(否定)隶属函数对不确定信息的描述缺陷.集对分析联系数函数能更有效地描述事物之间同(确定/真)、异(不确定及模糊/犹豫)、反(对立/假)之间的内在规律.偏联系数[5-11]是有效解决同、异、反联系分量的理想工具，它是联系数函数中的一种伴随函数.偏联系数立足系统矛盾运动之中，刻画微观层次中联系数的同、异、反趋向正向迁移或负向迁移的运动变化，是客观状态评价与系统微观趋势判定趋向综合分析的数学描述，偏联系数体现了事物微观与宏观普遍联系与处于运动的变化，包含了事物状态趋向的确定-不确定关系、临界的模糊及联系数结构动态信息的可变规律.目前较多学者从不同视角开展偏联系数的相关研究，已经取得了一定研究成果，但对偏联系数得分函数的研究仍处于空白，许多问题有待解决.

本文基于集对分析偏联系数理论，借鉴Vague集、直觉模糊集及犹豫模糊集、SPA集中得分函数[12-15]的相关思想，研究偏联系数的得分函数，给出了偏联系数得分函数的涵义、构造准则及相关特性.通过偏联系数的得分函数能较好解决联系数中确定-不确定正向趋向及不确定-对立的负向趋向动态变化及迁移偏向规律，克服传统联系数中得分函数刻画信息中证据变化的不足，同时避免了联系数中采用集对势对信息描述带来的信息丢失及不可区分的缺陷.

1 偏联系数及得分函数

偏联系数是集对分析联系数的一种伴随函数，它描述了联系数分量在微观迁移中趋向正向和负向的迁移变化.偏联系数主要是以联系数中当前较低(负、 偏负)层次和较高(正、 偏正)层次的联系分量的相互迁移构成的联系数系统结构的矛盾运动，这种矛盾运动在趋势演化上体现出类似集对势[1]中宏观上的同势、异势和反势，它不同于集对势的区别是：集对势是宏观演化态势，偏联系数是联系数分量趋于正向和负向态势微观的运动和变化，与宏观层次上的演化态势是相同、相异或相反的.基于偏联系数的哲学思路，从表面上观察联系数是静态的，而从微观上联系数的内容的分量依然处于运动变化状态.

虽然偏联系数是决策不确定信息时信息正向与负向迁移变化运动的伴随函数，但不能根据决策信息对某规则进行信息集结和决策，所以对一定决策信息(组)备选方案进行择优排序，用评价函数或构造得分函数进行描述或体现是合理有效的手段之一.目前学者提出了许多得分函数理论，应用于各领域解决决策优化问题，而对于偏联系数的得分函数的研究尚处空白，通过得分函数构造，希望决策者支持同(肯定)证据越多，反(否定)证据越少，体现决策价值方案越优，但对于偏联系数中异(犹豫/不确定)证据依据信息趋向出现的悲观、中立和乐观表现构造偏向同或反证据.因此偏联系数得分函数衡量了评价确定-不确定信息系统中决策方案对于决策偏向满足的一种标准，体现了集对分析中同、异、反信息的综合集结，得分函数是偏联系数决策的核心和关键，如何有效构造联系数得分函数直接影响不确定信息中多属性评价的正确与否.

1.1 偏联系数及得分函数

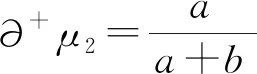
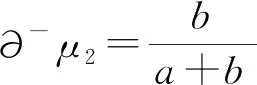
定义3设在二元联系数μ2=a+bi中，a,b∈[0,1],a+b=1,i∈[-1,1]，则称S∂μ2(μ2)=∂+μ2-∂-μ2为二元联系数μ2=a+bi的正负偏联系数得分函数.

S∂μ2(μ2)的值越大，得分函数的精度越高；S∂μ2(μ2)的值越小，得分函数的精度越低.S∂μ2(μ2)反映了二元联系数μ2=a+bi中对证据支持(同/肯定)与异(不确定/犹豫)的两种力量的对比，其值是确定的.在二元联系数中描述证据支持(同)与异(不确定/犹豫)采用的是同势[1]或同一度概念.同势反映了证据支持(同)的走向变化趋势，同势的概念具有很大的局限性，没有体现证据异(不确定/犹豫)对证据支持(同)的影响，因此利用同一度或同势会导致信息不完整和信息丢失.所以，通过定义得分函数衡量决策属性满足的程度从理论上要比采用同势或同一度的描述更加科学、合理、准确和有效.

二元偏联系数得分函数很容易扩展到三元偏联系数得分函数.

定义5设在三元联系数μ3=a+bi+cj中，a,b,c∈[0,1],a+b+c=1,i∈[-1,1],j=-1，则称S∂μ3(μ3)=∂+μ3-∂-μ3为三元联系数μ3=a+bi+cj的正负偏联系数得分函数.

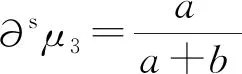
定义7[1]在三元联系数μ3=a+bi+cj中，当c≠0时，同一度a与对立度c的比值a/c称为势或集对势，用shi(u)=a/c表示；同一度a与对立度c的差值a-c称为减势或集对减势，用shi-(u)=a-c表示.

对于定义7，不论采用势或减势，在本质上是相同的，为了便于运算处理的需要，可以根据实际情况选择.

1.2 偏联系数得分函数构造准则

偏联系数得分函数在构造中包含了集对分析中确定-不确定系统的两部分信息，反映了对支持证据(同)与犹豫不确定证据(异)的正向与负向状态迁移变化，通过偏联系数得分函数能更直观地体现出迁移的量化.利用得分函数刻画集对分析信息要比集对势(同势、 异势和反势)更合理，集对势在理论上有很大局限性：其一，集对势定义了集对同一度与对立度的两种对比变化，但在势定义中无法体现集对的不确定度或犹豫度信息；其二，在联系数中，当对立度c=0时，势的定义是失效的；其三，势定义具有不可区分性.为了能更合理、有效地进行决策，有时还需考虑决策偏好、决策权重及决策情绪(悲观、 中立和乐观)等因素的影响，所以偏联系数得分函数S(x)应满足如下准则：

在三元联系数μA=aA+bAi+cAj，μB=aB+bBi+cBj中，其对应的偏联系数为α和β，则

准则1对乐观决策，shi-(u)>0；若S∂u(α)>S∂u(β)，则α≻β.

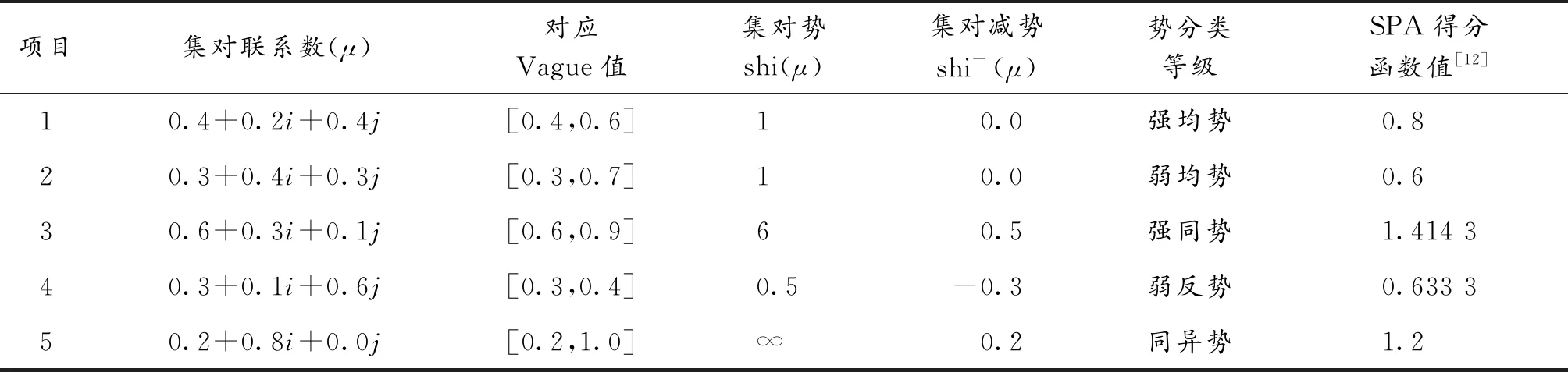
准则2对悲观决策，shi-(u)<0；若S∂u(α)

准则3对中立决策，shi-(u)=0；若S∂u(α)=S∂u(β)，则

( i )若μA=μB，则α=β；

(ii)若μA≻μB，则α≻β；

(iii)若μAμB，则αβ.

1.3 偏联系数得分函数的构造

在分析偏联系数及得分函数的基础上，本文构造一个新的偏联系数得分函数.

定义8对于三元联系数μ=a+bi+cj，其对应偏联系数为α，则定义偏联系数得分函数

其中，sign(x)为符号函数.符号函数能有效刻画决策中的悲观、中立和乐观心态.显然定义8的得分函数包含了集对分析中联系数同、异、反的信息，能有效地将确定-不确定信息系统中不同决策心态下的偏好趋向集结为得分函数，并利用得分函数对决策优劣进行排序.同时，该得分函数体现了决策时少数服从多数的原则及心理学决策中的“马太效应”[5].

得分函数S∂μ(α)满足准则1～3，同时具有如下性质.

性质1有界性：-1≤S∂μ(α)≤1.

对于二元偏联系数得分函数，由于a,b∈[0,1],a+b=1，从而

对于三元偏联系数得分函数，根据定义8分三种情况进行讨论：

( i )当a>c时S∂μ(α)=(a-c)+ab/(a+b).由于a,b,c∈[0,1],a+b+c=1，从而

(ii)当a

(iii)当a=c时S∂μ(α)=0.显然S∂μ(α)∈[-1,1].

综合上述三种情况即得性质1.

性质2单调性：偏联系数得分函数S∂μ(α)关于α是单调增函数.

从定义3、定义8易知：S∂μ(α)关于∂+μα是单调增函数，关于∂-μα是单调减函数，所以S∂μ(α)关于α是单调增函数.

2 示例分析

为验证构造的偏联系数得分函数的合理性、可行性和有效性，进行如下示例分析[12](表1).

表1 偏联系数得分函数分析

从表1可知：对集对联系数0.4+0.2i+0.4j和0.3+0.4i+0.43，其势值为1，减势为0，得分函数S∂μ(α)为0，反映出对支持证据(同)与对立证据(反)的正向与负向状态迁移是势均力敌状态，其正向与负向迁移变化应该是均匀变化，但联系数0.4+0.2i+0.4j的异同偏联系数(0.333)小于联系数0.3+0.4i+0.3j的异同偏联系数(0.571)，这说明联系数0.3+0.4i+0.3j中不确定信息偏向支持证据(同)要比0.4+0.2i+0.4j偏向支持证据(同)表现得更强；同理，联系数0.3+0.4i+0.3j中不确定信息偏向对立证据(反/否定)要比0.4+0.2i+0.4j偏向对立证据(反/否定)表现得更弱；当然从直觉模糊和认知思维分析，偏联系得分函数S∂μ(α)是合乎逻辑规律和符合实际要求的.偏联系得分函数能直观体现集对分析中同、异、反信息分量的迁移变化规律，而SPA得分函数无法体现迁移变化规律；偏联系数得分函数在势(shi(μ)=1)或减势(shi-(μ)=0)的情况下没有分辨率，但SPA得分函数有较好分辨率.

3 结束语

本文在集对分析偏联系数的基础上结合得分函数理论，给出了基于偏联系数的一种得分函数构造方法，并结合该方法讨论了偏联系数的得分函数准则和性质.该得分函数较好地解决了偏联系数中趋于联系数不同趋势变化的评价判断问题，从理论上刻画了决策信息中包含的同(乐观-肯定)、异(犹豫-不确定)、反(悲观-否定)决策偏好，是决策者对决策方案信息的真实表现和评定的有效体现.本文初步建立的偏联系数得分函数是对集对分析理论的拓展延伸，是对得分函数理论的补充，其相关理论还有待进一步深入研究讨论.