非线性随机偏害共生模型的动力学行为

孙 阳，郝 丹，艾晓辉

(1.哈尔滨理工大学 理学院，黑龙江 哈尔滨 150080；2.东北林业大学 理学院，黑龙江 哈尔滨 150040)

种群问题指种群的数量和密度随着时间推移变化的问题，是生物数学中不可或缺的一项研究内容.种群的密度调节有多种形式，一般可分为互惠性和对抗性，这两种形式之间还有一种过渡关系，如偏害共生关系，它是指物种之间相互作用仅使一方受到抑制(偏害)，而不影响另一方发展.2016年，熊焕焕等[1]建立了两种鱼群的偏害共生模型

但是，由于自然界实际情况复杂多变，线性模型能解决的问题非常有限.2018年，Wu[2]建立了如下非线性偏害共生模型：

(1)

其中Ni(t)>0(i=1,2)代表t时刻两个种群的物种数目；ri(t)(i=1,2)是非负数，表示t时刻种群內禀增长率；u>0表示第二类种群对第一类种群的抑制系数；Pi(t)>0(i=1,2)表示种群的最大环境容纳量；αk(t)>0,k=1,2,3.

近年来，偏害共生系统引起了国内外学者的广泛关注，2019年起，Guan等[3]、Zhou等[4]研究了一种具有Beddington-DeAngelis功能响应的偏害共生模型，通过将Allee效应引入第二个物种，对具有Allee效应的系统进行完整的定性和分支分析，并对覆盖了第一个物种的离散时间的偏害共生模型进行动力学分析；Luo等[5]、Li等[6]研究了对第二种物种具有强Allee效应的B-D功能反应的偏害共生模型的全局动力学及具有分布时滞但不具有离散时滞的系统的稳定性等.

然而，考虑自然环境干扰下偏害共生模型的研究并不多见，在现实自然界中，种群有时会受到诸如寒流、干旱等灾害的剧烈干扰.文献[7-10]指出，生态系统受到环境噪声的影响，种群的增长率和环境容纳量可能会急剧变化，使种群的生存环境从一种状态转换为另一种状态.考虑电报噪声对种群系统的干扰，用一个具有有限状态空间S={1,2,…,m}的连续时间Markov链γ(t),t>0描述这些生态系统中的随机因素.

令γ(t)的生成元是Q=(qij)，即

其中j≠i,qij≥0,i,j=1,2,…,m；并且

此外，种群还会受到一些突然出现的随机剧烈环境扰动，例如地震、传染病等，使得生物种群在短时间内发生很大的数量变化，从而破坏种群数量的连续性变化，因而用带有Lévy跳噪声的随机模型来描述这类现象.把电报噪声和跳噪声考虑在内，那么模型(1)就变成

(2)

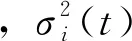
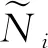
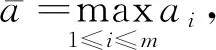
1 全局正解的存在唯一性

假设1对任意i∈S，存在正数C，使得

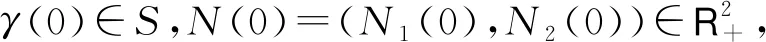
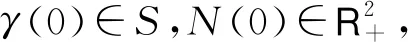
其中

由假设1可得

于是存在M>0，使得LV(N)≤M，因此公式(3)满足以下不等式:

对不等式(4)从0到τk∧T积分，并且两边取期望，得

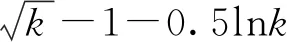
由上述不等式得到

这里IΩk代表Ωk的示性函数.令k→+∞，则∞=V(N(0))+MT<+∞，矛盾.于是τ∞=∞依概率1成立.】

2 物种的生存和灭绝阈值

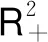
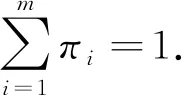
假设2存在一个正数G，使得

假设3对∀γ∈S有σi(γ)>0,i=1,2.

定理2如果对系统(2)的每个i(i=1,2)都有

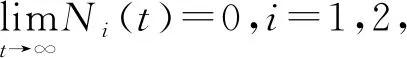
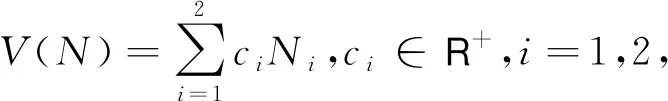
对函数lnV(N(t))继续利用It公式，得到

注意到

将上述不等式代入(5)式，有

也就是说，

其中

它们的二次变分为

由指数鞅不等式

及Borel-Cantelli引理可知，对几乎所有的ω∈Ω，都存在一个随机整数n0=n0(ω)，使得当n≥n0时，有

而当0≤t≤n,n≥n0时有

将(7)式代入(6)式得

同时，由假设2可知

同理

由局部鞅的强大数定律，有

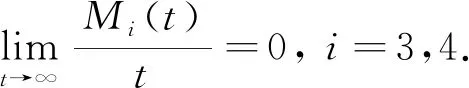
(9)

(8)式两边同时除以t，则当n-1≤t≤n,n≥n0时有

由(9)式以及Markov的遍历性，有

即种群灭绝.】

下面为了分析系统的随机持久性，首先给出系统解的矩有界性.

定理3在假设2、假设3下，对∀p∈(0,1)，都存在正数K，使得系统的解N(t)满足

证明定义Lyapunov函数

其中

因为G(N)是有界函数，所以存在常数K1，使得

G(N)≤K1.

(11)

对etV(N(t))利用It公式，再由(10),(11)式可得

对(12)式从0到τk进行积分，再取期望有

令k→+∞，则

E[V(N(t))]≤e-tV(0)+K1.

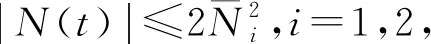
从而有

解的矩有界性证毕.】

为了得到随机持久性，先给出一些假设条件以及准备知识.

引理1[14]如果A=(aij)∈Zn×n，则以下结论是相互等价的：

( i )矩阵A是一个非奇异的M矩阵；

(ii)矩阵A的所有顺序主子式都是正的，即

(iii)矩阵A是半正定的，也就是说存在Rn中的向量p≫0，使得Ap≫0.

假设4存在某个状态u∈S，使得对所有的iu，都有qiu>0.

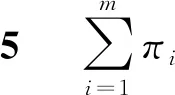
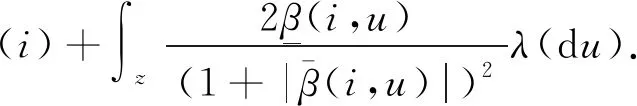
引理2在假设4和假设5下，存在一个常数θ>0，使得矩阵

A(θ):=diag(ξ1(θ),ξ2(θ),…,ξN(θ))-Q

是一个非奇异的M矩阵，其中ξi(θ)=θb(i).

证明由行列式的性质，不失一般性，在假设4中，设状态u=N，即qiN>0,1≤i≤N-1.容易看出

其中Mk(θ)是第一列元素ξk(θ)对应的代数余子式，即

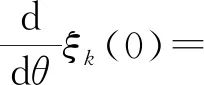
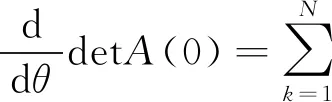
这就意味着

所以在假设4和假设5下，有

所以由(13)式有

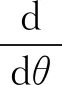
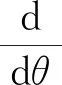
对每一个1≤k≤N-1，考虑矩阵A(θ)的顺序主子式

易知A(θ)∈Zk×k:={A=(aij)k×k,aij≤0,i≠j}.由(14)式知Ak(θ)每行元素的和都大于零，即

由引理1知，detA(0)>0，也就是说，矩阵A(θ)的所有顺序主子式都为正，故矩阵A(θ)是一个非奇异的M矩阵.】

定理4在假设2～5下，系统(2)的解N(t)随机持久.

证明首先由矩有界性，结合Chebyshev不等式，取M=K1/p/ε1/p，则

P{N(t)>M}=P{|N(t)|p>Mp},

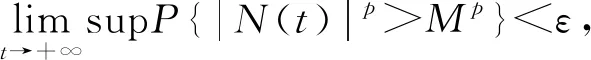
下面证明存在H>0，使得

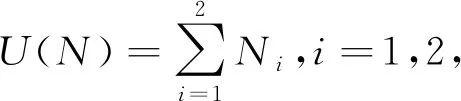
则

注意到引理2中的θ，结合引理1可知，存在一个向量p=(p1,p2,…,pN)T≫0，使得A(θ)p≫0成立，这等价于不等式

再令V2(N,k)=Pk(1+V1)θ，则

其中

由不等式(1+x)θ-1≤θx,x≥0,0≤θ≤1可得

从而

由(15)式，可选取充分小的η，使得

由(16),(17)式可知，存在M>0，使得

故

从而

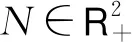
由此可推出

由Chebyshev不等式可证得

随机持久性得证.】

3 数值模拟

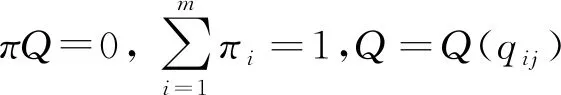
考虑模型

其中γ(t)是一个Markov链，其状态空间S={1,2}.模型(18)可以看做如下两个子系统:

π=(π1,π2)=(4/7,3/7).

下面利用文献[15-16]提到的Milstein数值模拟方法来支持理论分析结果.

例1在系统(18)中，令λ(dz)=1，初值N1(0)=N2(0)=50,α1=0.1,α2=0.2,α3=0.3,P1=2000,P2=500，系统的参数选取如下：

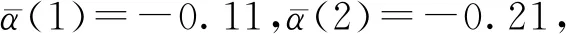
故此时系统(18)的系数满足定理1的条件，系统中的两个物种都会灭绝(图1).

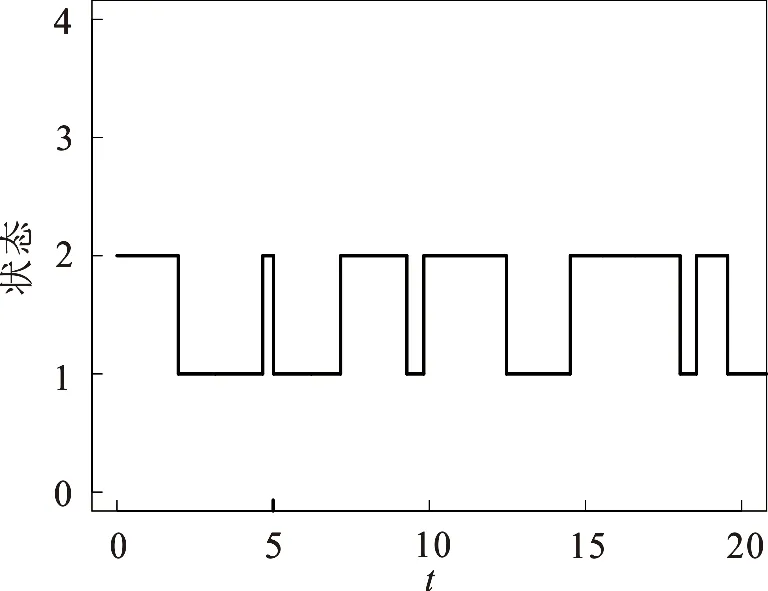
(a)Markov状态转换

例2在系统(18)中，令λ(dz)=1，初值N1(0)=N2(0)=50,α1=0.1,α2=0.2,α3=0.3,P1=2000,P2=100，系统的参数选取如下：

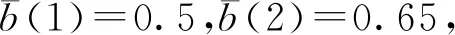
故此时系统(18)的系数满足定理4的条件，系统中的两个物种随机持久(图2).

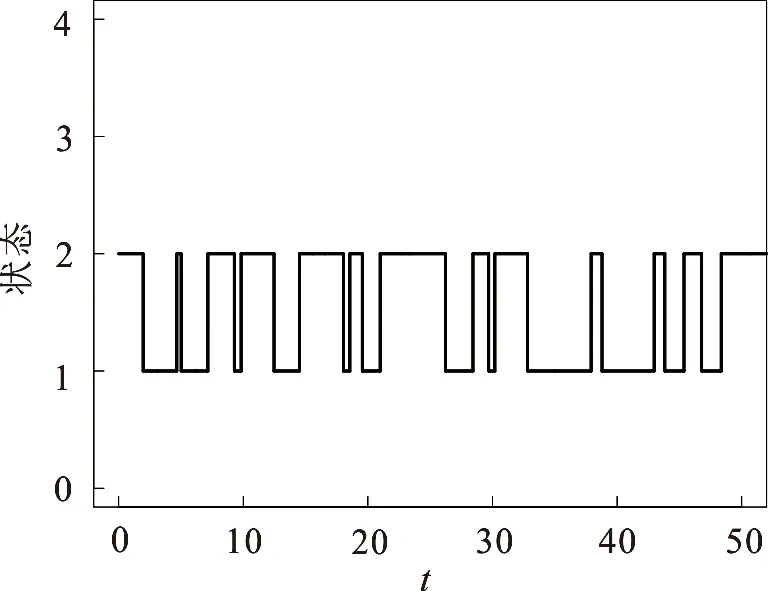
(a)Markov状态转换

4 结束语

讨论了偏害共生系统在加入了电报噪声和Lévy跳噪声的干扰后全局正解的存在唯一性以及灭绝性和随机持久的条件.利用马尔科夫链来模拟电报噪声，由于其具有状态转移的特性，在它的调节下，子系统可能一个是灭绝的，一个是持久的，然而最后可能依然会随机持久.值得一提的是，对于系统本身起决定作用的是种群的內禀增长率，这对于未来种群的研究要有一定的参考意义.