轴向运动梁在横向裂纹作用下的Green函数解

赵 翔，王 琦

（西南石油大学土木工程与测绘学院，成都 610500）

引 言

轴向运动梁是一种重要的工程简化模型，广泛应用于电梯、传送带、磁带、带锯、编织纤维等领域[1]。Mote[2]率先提出了轴向运动梁的动力学模型，并对影响结构稳定性的因素进行了分析。此后，围绕轴向运动梁的动力学特性，众多专家学者对轴向运动梁展开了一系列研究[3-5]。Stylianou 等[6]利用有限元模型，研究了轴向运动梁的动力学稳定性问题。Öz 等[7]研究了梁的轴向加速度、弹性和张力的动态响应，发现当梁的速度变化频率接近结构固有频率的2倍或为其中两阶频率之和时，系统会失稳。Huang 等[8]使用增量谐波平衡(IHB)方法来评估轴向运动梁的非线性动态行为。Chang 等[9]利用有限元法研究了轴向运动Rayleigh 梁的振动特性和稳定性，发现在动态特性方面Rayleigh 梁模型比Euler 梁模型更准确。Mao 等[10]研究了谐波激振力和内共振条件下超临界轴向运动梁的局部和全局共振。Yang 等[11]将TVRBSE 模型应用于悬臂Rayleigh 梁轴向运动和旋转的动态分析。Yang 等[12]提出了寻找轴向运动梁近似固有频率的参数分析方法。Karličić 等[13]通过分析轴向运动梁的动力学模型，发现非线性项对频率响应和结构振幅的降低有显著影响。

在轴向复合梁领域，Tang 等[14]提出了研究粘弹性梁动态参数共振的方法，并将其应用于动态稳定性分析。Ebrahimi-MaMaghani 等[15]分析了粘弹性轴向功能梯度（AFG）梁的结构动力学特性和振动稳定性。Ghorbanpour 等[16]采用Galerkin 法研究了气动压力和轴向运动特性对夹层结构振动的影响。Li等[17]研究了轴向运动粘弹性夹层梁的非线性强迫振动和稳定性。

在实际工程环境中，构件的损伤问题普遍存在，通常带裂纹工作[18]。轴向运动的构件也会受到裂纹影响，通常表现为结构刚度和动力性能的下降[19]。因此，有必要对轴向运动的裂纹梁进行研究。Sarigül 等[20]研究了弹簧梁系统的固有频率，发现固有频率随着裂纹深度的增加而降低。Murphy 等[21]研究了固定支撑之间水平运动裂纹梁的振动和稳定特性。Bachaya 等[22]利用哈密顿原理和Galerkin法研究了轴向速度、裂纹深度以及材料性能指标与固有频率之间的关系。杨鄂川等[23]利用传递矩阵法分析了裂纹和轴向运动的参数对梁振动频率的影响。

综上所述，以往的研究大多没有考虑裂纹，即使考虑了裂纹也忽略了速度和裂纹共同作用以及裂纹之间相互作用对挠度的影响。事实上，带裂纹的梁产生较大挠度往往意味着构件的失稳和破坏。本文在前期研究[24-25]的基础上探讨了轴向运动梁在横向裂纹作用下的Green 函数，通过数值计算验证了解决方案的有效性，并讨论了各种几何物理参数的影响。

1 轴向运动梁的Green函数

图1所示为轴向运动裂纹梁的力学模型，其中L为梁长，b为梁宽，h为梁高，Lc和hc分别为裂纹梁的裂纹位置和深度，v是轴向运动速度，x0是施加载荷的位置，P0eiΩt是施加的简谐激励。

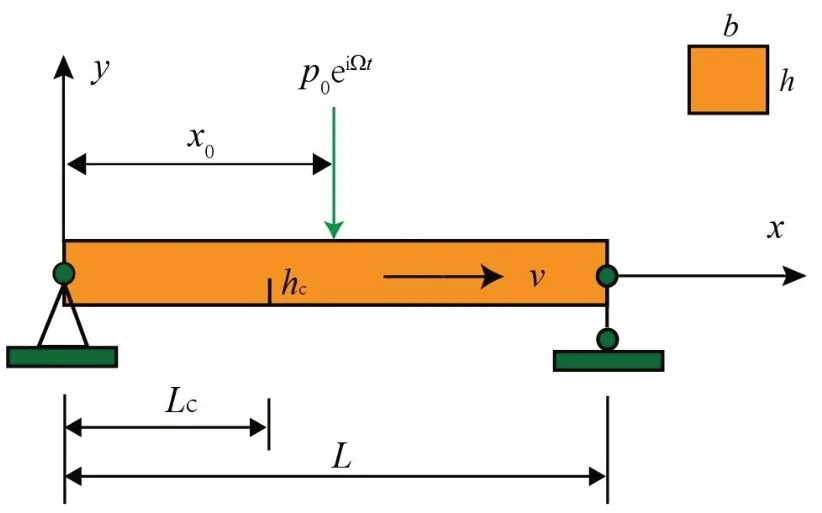
图1 轴向运动裂纹梁力学模型

为获得轴向运动裂纹梁的动力响应，得求解出轴向运动梁的Green函数，其控制方程为[26]：

其中，EI和ρA分别是梁的抗弯刚度和单位长度质量，v是轴向运动速度，ρI为转动惯量，w(x,t)是梁的挠度，p(x,t)表示施加在梁上的载荷。假设轴向运动梁受到一个简谐载荷p(x,t) =p(x)eiΩt，则式(1)的稳态解可以写成简谐位移w(x,t) =W(x)eiΩt的形式，其中W(x) 为稳态位移。消除式(1)中时间变量t，稳态位移可表示为：

其中，

从Green 函数的物理意义来看，G(x,x0)是以下微分方程的解：

其中，δ(·)是狄拉克函数。因为Green函数表示任意一点激励的响应，所以均布载荷的响应可利用叠加原理表示为：

其中，P(η) 为力的大小，G(x;η) 为Green 函数。为获得Green 函数，利用拉普拉斯变换方法求解式(4)，并将基本解表示为：

其中，H(x-x0)是单位阶跃函数，ϕi定义为：

式(7)中，si为特征方程的根，Ki定义为：

2 裂纹梁的Green函数

多裂纹梁的思想是通过裂纹将梁划分为若干梁段，有n个裂纹就会有(n+1)个梁段以及(n+1)个局部坐标系[24]，如图2所示。

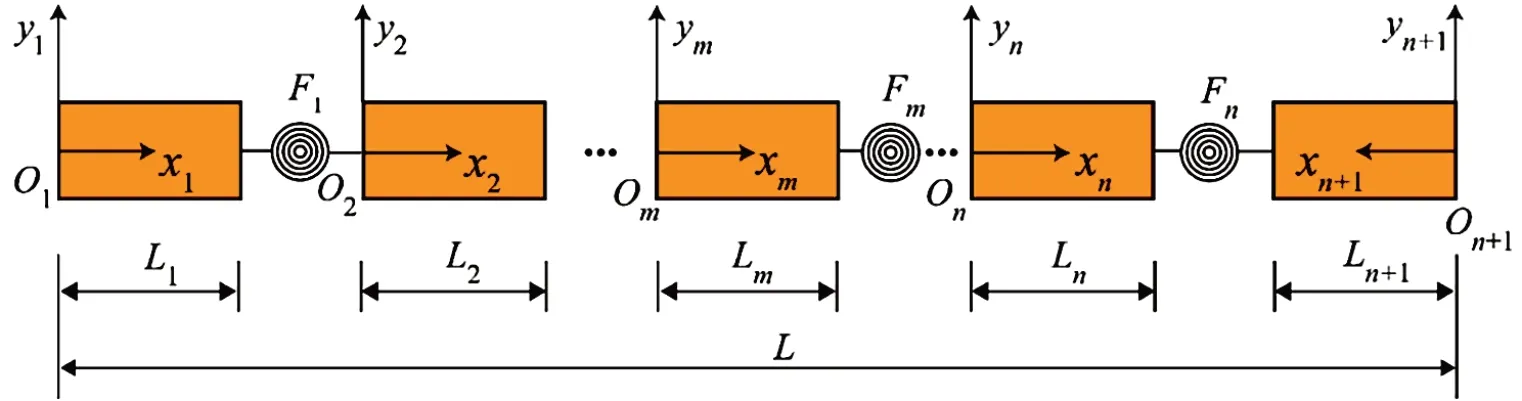
图2 多裂纹梁力学模型

在这些坐标系中，每个梁段都有如下Green函数：

其中，

是待确定的常数。为了便于标注，引入了以下向量：

其中，i的范围从1 到n+ 1。对于每个梁段，Green函数中包含4个未知常数（见式(9)）。因此，对于有n个裂纹的梁，总共有4(n+1)个常数或n+1 个矢量Ui需要确定。通过确定这些常数或矢量，就可以得到裂纹梁的Green函数。

2.1 裂纹截面处的传递关系

根据文献[24]，在裂纹位置(xi=Li-,xi+1= 0+)处，梁的挠度和弯矩应分别相等；剪切力大小相等，方向相反；转角是不连续的。并且在i( 1 ≤i≤n)个裂纹截面处有如下传递关系：

其中，Fi是等效无质量扭簧的弹性常数。将式(9)代入式(12)中可得

其中，

将式(13)写成如下矩阵形式：

其中，

由式(15)可知，第i(1 ≤i＜n)个截面处建立如下传递关系：

同理，则在第n个裂纹截面处的传递关系表示如下：

将式(9)代入式(18)，可以得到以下矩阵形式的方程：

其中，

其中，

因此，第n个裂纹截面处传递关系为：

2.2 确定未知常数

接下来将通过式(17)和式(22)建立U1和Un+1之间的关系，然后用梁的边界条件来确定未知常数。以简支多裂纹梁为例，有：

即在局部坐标系O1x1y1和On+1xn+1yn+1中，梁左右两端的位移和弯矩为零，因此U1和Un+1可以表示为：

由式(17)可得U1和Un之间的关系为：

因此，常数B1、D1、Bn+1和Dn+1可以从向量方程式(26)中获得，它实际上代表4 个代数方程。因此，可以完全确定矢量的大小。式(17)和式(22)中的向量Ui(i= 1,2,3,…,n)都可以通过这种方法确定。

2.3 坐标变换

为了获得全局坐标系中的Green 函数，将局部坐标转换为全局坐标，可以得到n个裂纹轴向运动梁的Green函数为：

3 数值分析与讨论

一根两端简支的轴向运动裂纹梁，梁高为h，梁长为L，在x0=L/2 处受到集中力p(x,t)=δ(x-L/2 )eiΩt作用。为了便于说明，本文引入以下无量纲化参数：

其中，wsmax=L3/(48EI)是简支梁受到单位集中力产生的最大静挠度，Ω0= π2/L2是EB 的一阶固有频率，L'=Lc/L∈[ -0.5,0.5 ]表示从曲梁中部测量的无量纲裂纹位置，即在梁中间界面左（右）侧为负（正）的位置，h'为相对裂纹深度。以下所有的计算都是基于E= 7.0 × 1010Pa进行的。

3.1 解的有效性验证

为了验证单裂纹梁强迫振动解析解的有效性，建立了图3所示的ABAQUS 模型。该模型采用实体单元C3D8R 对三维梁进行离散化，元素的数量为20 112，节点的数量是24 395。此外，在裂缝附近对网格进行了细化，以提高计算精度。

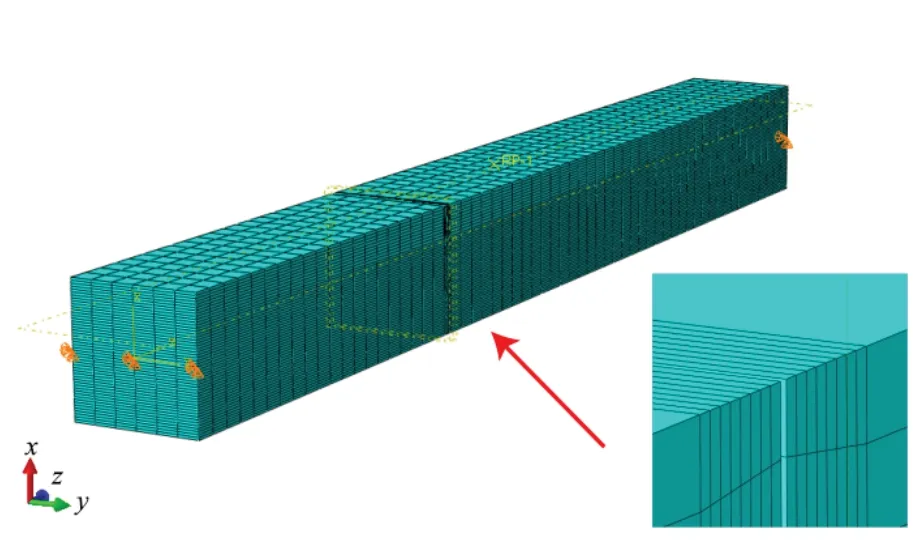
图3 裂纹梁有限元模型

图4 所示为当前方案与文献[24]结果和有限元仿真结果的对比情况，其中虚线代表裂纹位置。从图4 中可见，现有文献[24]的结果和3D-FEM 有限元的散点分布于本文结果的附近，从而验证了本方案的有效性。

图4 跨中作用单位简谐集中力的挠度（图中虚线为裂纹位置）

3.2 轴向运动速度的影响

图5 所示为不同轴向速度v下的无量纲化的挠度g(ξ; 0.5) 曲线。从图5 中可以看出，随着轴向运动速度v的增加，g(ξ; 0.5) 逐渐减小。此外，在速度v较小时，裂纹效应明显，随着v逐渐增大后，曲线g(ξ; 0.5) 尖点趋于消失，这表明轴向速度v对裂纹梁的振幅有一定的抑制作用。

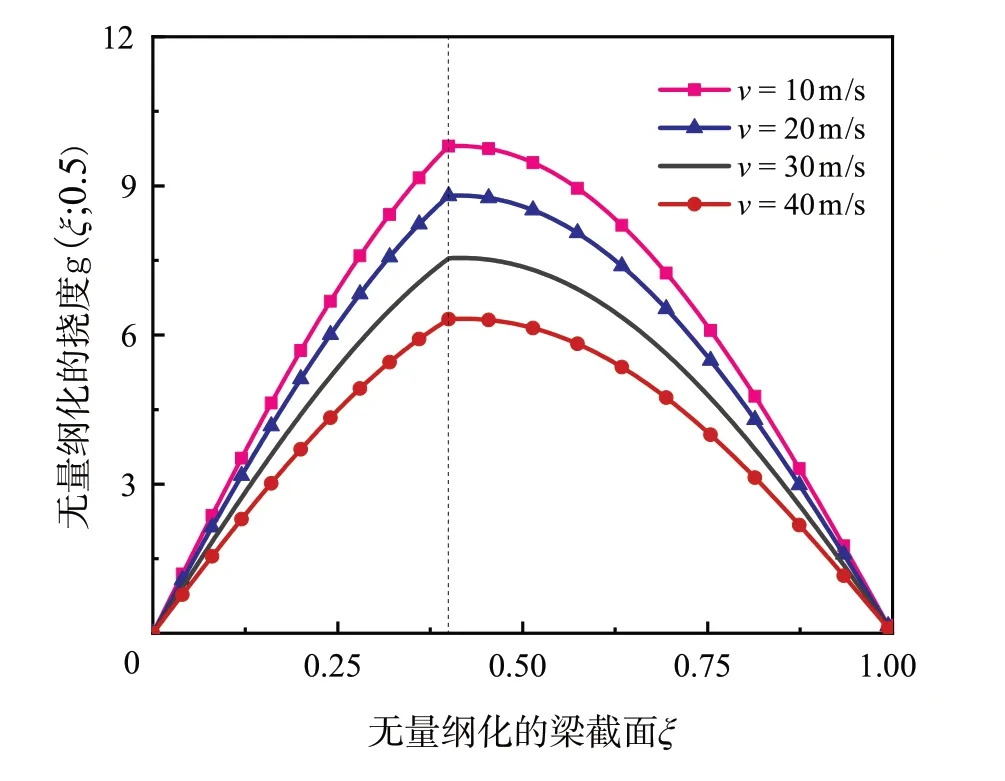
图5 不同轴向速度v下的挠度g(ξ; 0.5)（图中虚线为裂纹位置）

3.3 裂纹位置的影响

图6所示为不同相对裂纹位置L'的无量纲化的挠 度g(ξ; 0.5) 。从 图6 中 可 以 看 出，L'= 0 时，g(ξ; 0.5) 对称于ξ= 0.5，g(ξ; 0.5) 最大值发生在跨中。随着相对裂纹位置向支座靠近，g(ξ; 0.5) 最大值也逐渐增加。在L'= -1/5 时，尖点尤其明显，表明在轴向速度和裂纹共同作用下，远离跨中的部分区域振幅大于跨中，即裂纹处是受力的薄弱点。

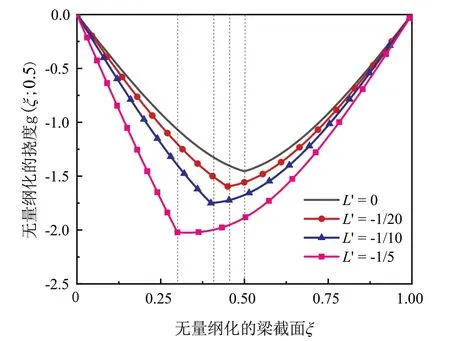
图6 不同裂纹位置L'的挠度g( ξ; 0.5)（图中虚线为裂纹位置）

3.4 裂纹深度的影响

图7所示为不同相对裂纹深度h'下的无量纲化的挠度g(ξ; 0.5) 。从图7 中可以看出，当相对裂纹深度h'较小时，曲线平滑且关于ξ= 0.5 对称，挠度g(ξ; 0.5) 最大的位置发生在跨中。然而随着相对裂纹深度h'的增长，挠度g(ξ; 0.5) 由1.20 增大到1.75，最大值发生在裂纹处，且图像出现尖点，这说明即使在轴向速度作用下，裂纹深度依然极大地削弱了梁的承载力，使g(ξ; 0.5) 最大值由跨中转移到裂纹位置。

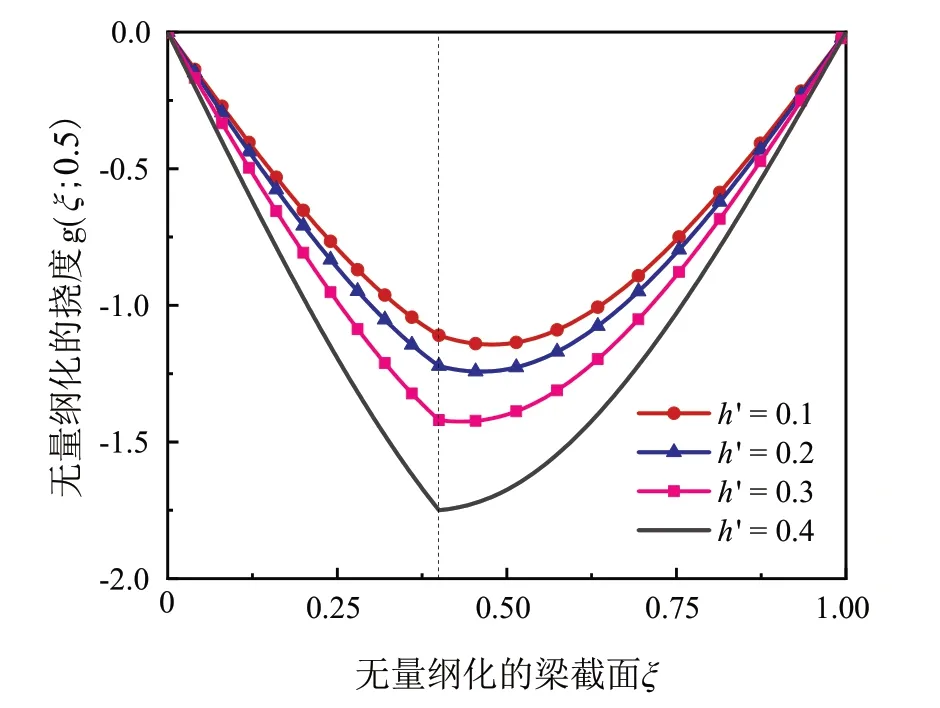
图7 不同裂纹深度h'的挠度g(ξ; 0.5)（图中虚线为裂纹位置）

3.5 裂纹相互作用的影响

g(ξ; 0.5, ± 1/5 )表示两个裂纹深度相同并且位置关于ξ= 0.5 对称的Green 函数，g(ξ; 0.5, + 1/5)和g(ξ; 0.5, - 1/5 )各自为有一个裂纹的Green 函数，g(ξ; 0.5 )为 二 者 的 累 加。 从 图8 中g(ξ; 0.5, ±1/5 )、g(ξ; 0.5, +1/5 )和g(ξ; 0.5, -1/5)

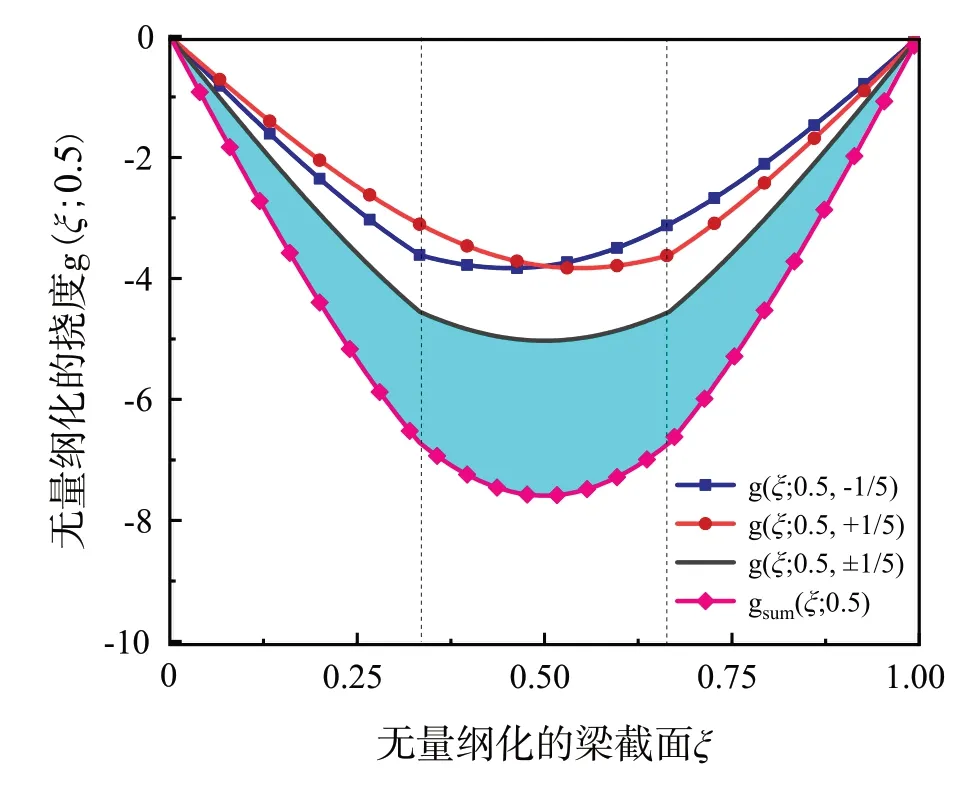
图8 两裂纹相互作用的挠度（图中虚线为裂纹位置）

图8 所示为两裂纹相互作用的无量纲化的挠度g(ξ; 0.5) 。曲线可以看出，双裂纹的挠度明显大于单裂纹，表明对称双裂纹的削弱能力强于单裂纹，这是符合物理实际的。此外，g(ξ; 0.5, ± 1/5 )和g(ξ; 0.5 )之间的蓝色填充区域表示两个裂纹之间相互作用的强度，面积越小，两个裂纹之间的相互作用越明显，反之亦然。

4 结 论

本文研究了轴向运动梁在横向裂纹梁作用下的Green 函数解，讨论了轴向运动速度、不同裂纹位置、裂纹深度和裂纹相互作用对挠度的影响，并得出以下结论：

1)轴向运动速度与梁的挠度呈负相关，轴向速度增大，g(ξ,0.5 )逐渐减小，同时裂纹效应减弱，这表明轴向速度的增加对减小挠度有一定的积极作用。

2)裂纹深度较大时，受力的薄弱点（尖点）随裂纹位置变化，尖点位置随裂纹位置从L'= 0变到L'=-1/5，充分展示了裂纹位置对动态特性的影响。

3)裂纹深度对梁承载力的削弱明显，在相对裂纹深度从h'= 0.1加深到h'= 0.4的过程中，Green函数g(ξ,0.5 )逐渐增大，梁的刚度显著下降。

4)在同等裂纹深度下，对称双裂纹的曲线g(ξ,0.5, ± 1/5 )大 于 各 自 带 一 个 裂 纹 的g(ξ,0.5, - 1/5 )和g(ξ,0.5, + 1/5 )，这说明对称的双裂纹的削弱能力强于单裂纹。此外，两条裂纹的相互作用可用曲线g(ξ,0.5, ± 1/5 )和gsum(ξ,0.5 )所围成的面积表示，面积的大小反映了相互作用的强度。

文中所研究的理论公式可为相关领域的分析和计算提供理论参考，也可应用于一些先进结构的损伤诊断以及控制和修复技术。