基于VMD-DE-ELM的同杆双回输电线路故障识别

邹 西，吴 浩，邓思敬，漆知渊，宋 弘

（1.四川轻化工大学自动化与信息工程学院，四川 宜宾 644000； 2.人工智能四川省重点实验室，四川 宜宾 644000； 3.阿坝师范学院电子信息与自动化学院，四川 阿坝州 623002）

引 言

随着人口数量增长，可占用的土地日益减少，同杆双回输电线路由于占地少、建设速度快、经济效益高等特点，大量应用在建设当中。同杆双回理论上存在120种故障，其中ΙA-ΙΙA、ΙB-ΙΙB和ΙC-ΙΙC这3 种故障类型的故障特征和正常情况一样，从电气上无法识别[1]；现在主要研究117 种故障类型，其故障类型分别为22 种单回路故障类型和95 种跨线故障类型[2]。在输电线路中发生跨线故障几率很小，但线路如果发生了跨线故障会造成严重后果[3]。

众多学者在同杆双回输电线路进行了大量研究[4-7]。文献[8]先通过对站域信息实行接地距离保护优化，再经过断路器和接地刀闸的位置信息自适应调整参数；最后通过选线结果对故障相进行邻线零序电流自适应补偿，对非故障相不进行补偿。该方法只针对了两个单回线的故障进行分析，未涉及跨线故障分析。文献[9]对故障线路特征信息等效成彼得逊模型进行分析，再根据区内/外故障电流行波相位差有所不同，引入S 变换计算电流行波差来实现故障识别，但该算法的容错性较差。文献[10]根据区内外故障与波阻抗及差波阻抗有所不同，引入比率制动系数进行故障识别。但需要根据不同的模量进行计算，操作比较繁琐，可靠性较差。文献[11]通过对初始行波电流变换规律，引入多分辨奇异值分解和随机森林对区内/外故障进行识别，但是算法抗噪声能力一般。文献[12]通过对不同的电压等级进行分析，根据各复合序网列出方程组计算序电流和序电压，再计算出其断口电压和相电流进行故障识别。但是该方法计算比较复杂，适应性较差。文献[13]根据近故障端的前行波电流波形和远故障端的反行波电流波形之间具有相似度关系，采用滑动窗的方法提取余弦相似度系数作为特征向量输入到概率神经网路进行故障识别，但是算法抗干扰能力较差。

现研究思路主要是通过对工频量、暂态量以及机器学习进行故障识别，工频量方法的可靠性强，但识别速度慢；暂态量方法的识别速度快，但可靠性差；而机器学习能够综合两者优点，因此本文使用机器学习算法对故障进行识别。为了提升同杆双回线路故障识别的稳定性和准确性，本文参考文献[14-15]中的分析方法，对区内外故障电压反行波变化规律进行分析，提出了一种基于变分模态分解和差分进化算法优化极限学习机（Variational Mode Decomposition & Differential Evolution & Extreme Learning Machine，VMD-DE-ELM）的同杆双回输电线路区内/外故障识别方法。该方法首先利用VMD将故障后一段时窗内的电压反行波分解到5个尺度上，特征提取对应尺度下的能量熵组成特征向量；其次，针对区内/外故障样本具有不平衡性，通过使用SMOTE 算法对区外样本进行扩充；最后，将特征向量集输入到DE-ELM 网络，验证本文算法对区内外故障识别的准确性。该方法为同杆双回线路的故障识别提供一种新思路。

1 反行波传输特征分析

同杆双回线路模型如图1 所示，M、N 两端为其母线，L1和L2为区内保护线路；L3和L4为区外保护线路；R1—R6为区内外保护检测单元。

图1 同杆双回线路仿真模型

1.1 区内单回路故障

以单回线路故障为例，当K1处发生故障时，区内故障产生暂态行波传输过程如图2 所示。图2 中τM和τN为故障点到两端的时间；MN 两端传输的总时间为τ。uMf和uNf为前行波，uMb和uNb为反行波。由图2 分析可知，当发生区内故障时，uMb和uNb先在两端保护单元检测到。若线路一端检测到反行波时间为t，另一端能够在[t,t+τ]时间内检测到反行波。

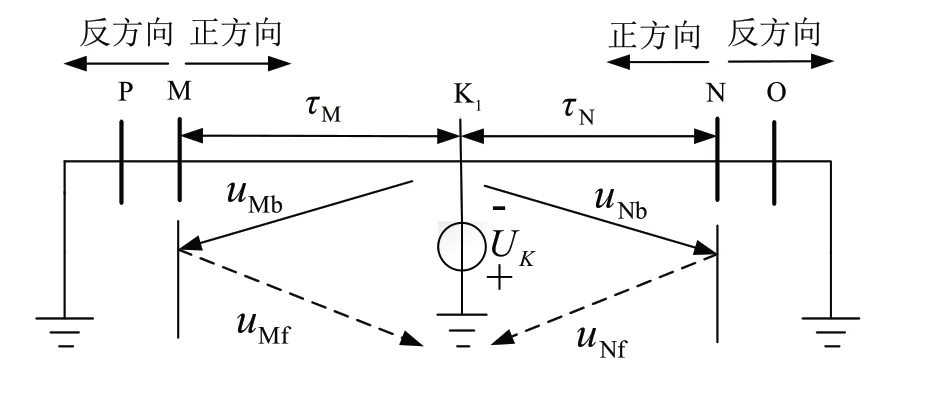
图2 区内单回路故障行波传输过程

1.2 区外故障

当K2处发生故障时，区外故障产生暂态行波传输过程如图3 所示。当发生故障后，uNf前行波在N端行波单元检测到，行波传输过程不会发生中断，uNf能够一直传输至M端，uNf在M端变为uMb反行波，uMb在M 端物理边界发生反射进行传输，反射之后uMb变为uMf前行波，uMf前行波会在线路上不中断传输至N 端，最后uMf前行波就变成了N 端uNb反行波[14]。

图3 区外故障暂态行波传输过程

由图3可知，发生区外故障时，若前行波uNf在N端检测到的时间为t，则在[t,t+ 2τ)内，反行波uNb理论上在N 端检测不到，而反行波uMb却能在M 端检测到。

1.3 反行波计算公式

两端的电压反行波如式(1)所示：

其中，Zc为线路上行波阻抗，uM、iM、uN、iN分别为M、N端电压和电流。

2 算法实现

提取同杆双回线路两端的电压、电流数据进行相模变换，选择同向1模量计算其电压反行波，再选取故障后[τ,2τ)时间内电压反行波进行VMD 分解，特征提取对应尺度下的能量熵组成特征向量，使用SMOTE 算法对区外故障样本进行扩充后，再将特征向量集输入到DE-ELM 分类器进行训练和测试，最后实现区内外故障识别。

2.1 相模变换

在同杆双回输电线路中存在大量耦合现象，为了减少其对线路的影响，使用相模变换矩阵进行解耦，将耦合的线路分解成独立的单相系统[15]，其解耦矩阵如式(2)所示[16]。

其解耦变换关系如式(3)所示：

其中，uT0、uT1、uT2、uF0、uF1、uF2分别为同向和反向的0模、1模和2模量电压。

2.2 变分模态分解算法

变分模态分解（VMD）算法对模态的中心频率和带宽能够自适应匹配，能实现固有模态分量（IMF）有效分离，其中心思想是构建和求解变分问题[17]。VMD将信号分解为K个IMF的步骤如下：

其中，f(t)为分解的信号，uk为第k模态分量，脉冲函数为δ(t)，ωk为对应第k个中心频率。

变分模态分解的过程如下：

2）更新{βk}和{ωk}，如式(5)～(6)所示：

3）更新λ，如式(7)所示：

重复式(4)～(7)的过程，直至满足式(8)，迭代停止，结束循环，得到本征模态函数。

其中ε为其精度（ε＞0），若不满足，则返回到步骤2）；若满足，则输出K值。

VMD 分解需要确定IMF 的个数K，如果分解个数K值不合适，则会导致结果偏差过大，本文使用中心频率法来预估K值。若VMD 分解中有IMF 的中心频率很接近，则认为VMD 出现过分解的情况[18]。表1列出了保护区外A、C相发生短路接地故障不同K值的中心频率，由表1 可知当K=6 时出现了过分解，因此本文选取VMD 分解的IMF 个数K=5。另外，区内故障分解模态个数也相同。

表1 区外故障不同K值的中心频率

2.3 电压反行波故障分析

2.3.1 区外故障分析

保护区外发生A、C相短路接地故障后[τ,2τ)内电压反行波信号波形如图4(a)所示，图4(b)和图4(c)为VMD 分解波形。图4(a)可以看出，在[τ,2τ)时间内电压反行波信号只能在M 端处检测到，而另一端不能检测到电压反行波信号；图4(b)和图4(c)比较可知，其两端对应尺度下电压幅值相差较大，电压能量分布较分散。

图4 保护区外波形分析

2.3.2 区内故障分析

保护区内L1线路发生A、C 相短路接地故障后[τ,2τ)时间内电压反行波信号波形如图5(a)所示，图5(b)和图5(c)为VMD 分解波形。图5(a)可以看出，在[τ,2τ)时间内两端都能检测到电压反行波信号；图5(b)和图5(c)比较可知，反行波经过VMD 分解后，两端对应尺度下电压幅值相差不大，电压能量分布比较集中。

图5 保护区内波形分析

2.4 能量熵特征提取

能量熵主要反映能量分布均匀性，若IMF 中所含频率复杂，则表明能量分布混乱，能量熵较大。

能量值计算如式（9）所示：

其中，两端第n个IMF能量值为EM,n、EN,n；两端第n个信号变换系数为WM,n(t)、WN,n(t)。故障起始时刻为t0；M、N 端之间传输的时间为τ；根据线路的长度和信号传输的速度，τ取值为1 ms。

通过对两端电压反行波信号进行分解获得n个模态分量，通过计算每个IMF 的能量分别为E1，E2，…，En。

其中，pi=EM,i/E和qi=EN,i/E分别为两端分解后第i个IMF的能量占总能量E的百分比。HM,i、HN,i分别表示M、N 端分解后第i个IMF的能量熵（i= 1,2,…,5）。当发生区内故障时，两端反行波电压分解后能量分布不均匀，且两端对应尺度下模态分量的能量熵相差不大；当发生区外故障时，其M端反行波电压分解后能量分布不均匀，而N端则相反，且两端对应尺度下模态分量的能量熵相差较大。基于此差异性，将特征向量[HM,1,HM,2,HM,3,HM,4,HM,5,HN,1,HN,2,HN,3, ]HN,4,HN,5输入到DE-ELM模型进行故障识别。

3 基于差分进化算法优化极限学习机故障识别

3.1 SMOTE算法

SMOTE 算法可用于处理样本不平衡的数据，而其思路是在相邻的少数样本使用随机线性插值来增加样本数量。

设pi=[xi1,xi2,…,xin]T为所需扩充的样本集，n为样本的个数，使用K 近邻法确定pi的k个邻近样本[19]，新的pj样本可由式(11)所得。

其中，rand(0,1)表示在0～1 之间的随机数；pj（j=1,2,…,l）为经过SMOTE算法后扩充的样本。

3.2 差分进化算法优化极限学习机

3.2.1 极限学习机

极限学习机[20]网络结构模型如图6 所示，图中设置ELM 网络输入层节点数为2，中间层节点数为21，输出层节点数为2。输入参数为区内故障样本和区外故障样本；输出参数为训练集和测试集准确率。

图6 ELM网络结构

图6 中，x=[x1,x2,…,xn]T(xi∈Rn)为数据的输入；y=[y1,y2,…,yn]T(yi∈Rn)为数据的输出，则：

其中，βi和ωi为两个层的权重，βi=[βi1,βi2,…,βim]，ωi=[ωi1,ωi2,…,ωin]，bi(i= 1,2,…,l) 为 隐 含 层 中 阈值。将式(12)变形为：

其中H=[g(ω1x+b1),g(ω2x+b1),…,g(ωlx+b1)]为矩阵的输出。最后通过使用最小二乘算法可以得到权重β[21]。

3.2.2 差分进化算法

差分进化算法是一种全局寻优算法，相比于其他算法，其参数很少、鲁棒性很强[22]，应用广泛, 差分进化算法流程如图7所示。

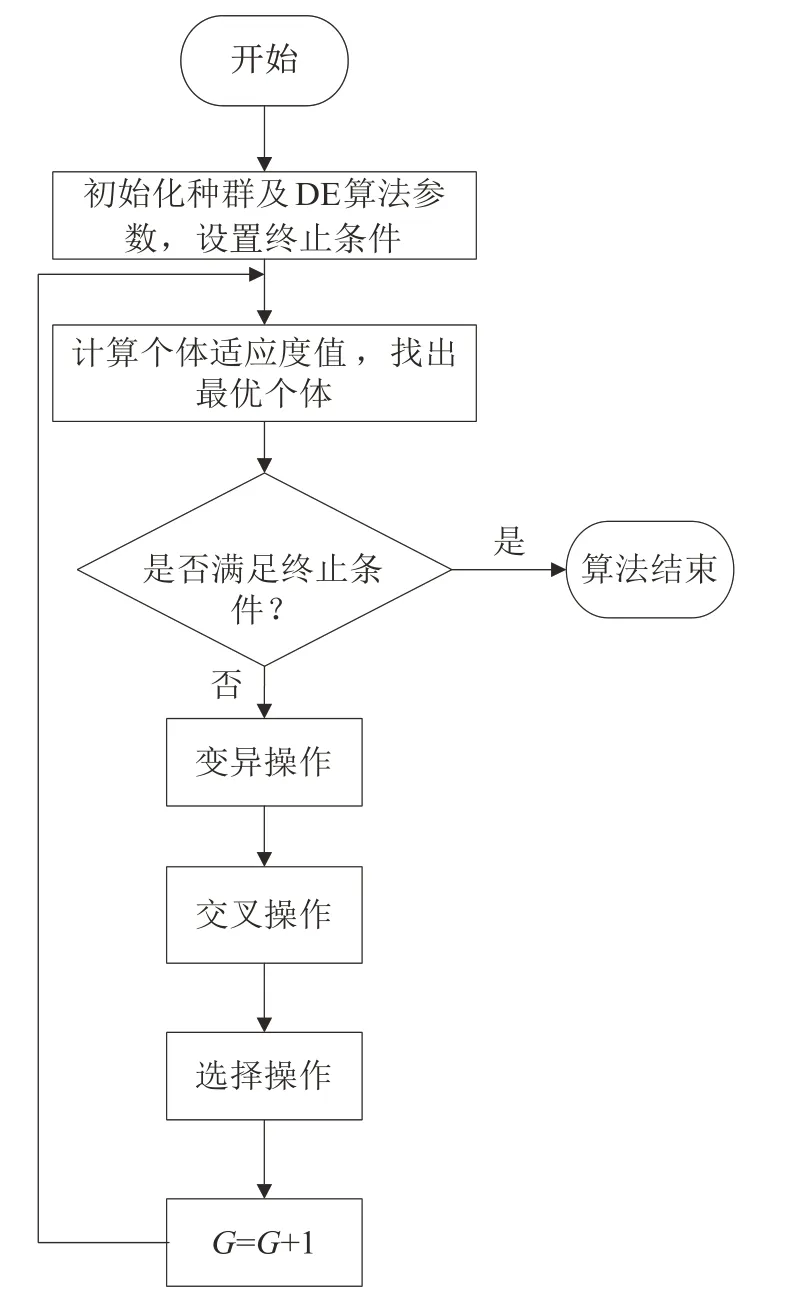
图7 差分进化算法

3.3 故障识别流程

故障识别流程如图8所示，其具体步骤如下：

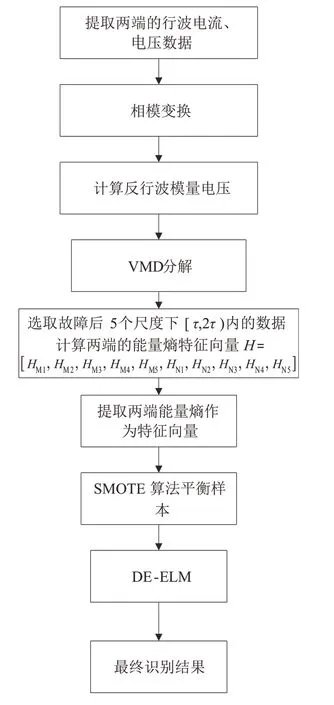
图8 故障识别流程

1）将行波电流、电压数据导入到Matlab；

2）进行相模变换；

3）计算反行波模量电压；

4）对反行波模量电压进行VMD分解；

5）选取 故 障 后5 个 尺 度 下[τ,2τ) 内 的 数据进行计算两端的能量熵特征向量H=[HM1,HM2,HM3,HM4,HM5,HN1,HN2,HN3,HN4,HN5]；

6）提取两端各尺度下能量熵作为特征向量；

7）SMOTE算法平衡样本；

8）将特征向量输入到DE-ELM 网络进行故障识别；

9）最终识别结果。

4 仿真验证

在PSCAD 软件上搭建仿真模型（图1）。区内MN 线路长为300 km，区外PN 线路长为150 km。采样频率为200 kHz，电压等级为500 kV，线路频率为50 Hz。

4.1 训练样本构成

区内故障样本：故障位置为距离N 端150 km；117种故障类型；设置10种不同的故障初始角，得到1170组区内故障样本。

区外故障样本：故障位置为距离N 端100 km；11 种故障类型；设置10 种不同的故障初始角，经过SMOTE算法平衡样本，得到1100组区外故障样本。

4.2 训练集识别结果

将区外扩充后的训练样本输入到DE-ELM 网络进行训练，得到一个DE-ELM 模型，其识别结果如图9所示。

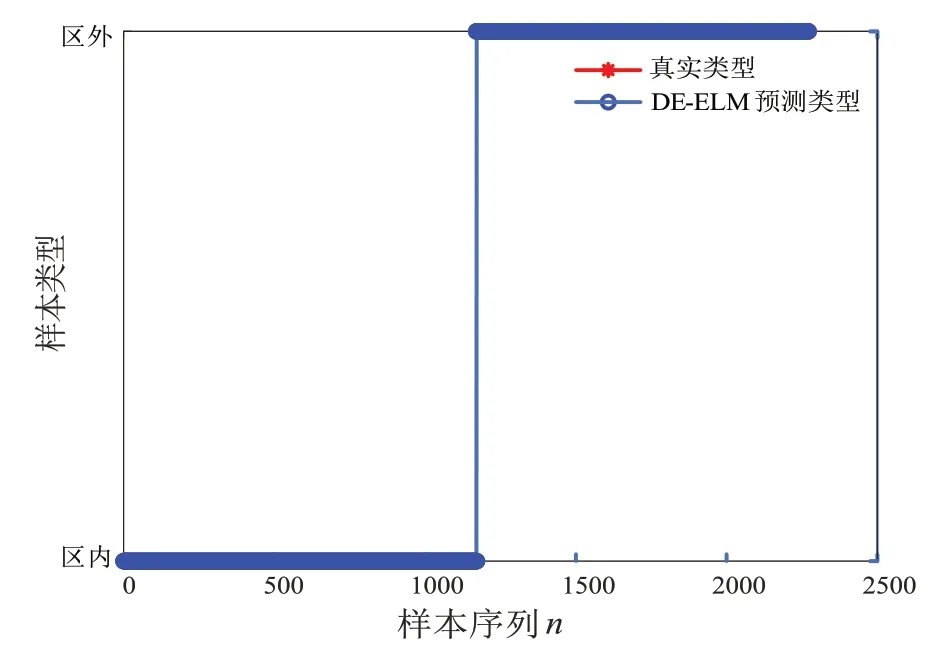
图9 训练集识别结果

4.3 算法测试

为了测试算法识别情况，选取区内故障26组和区外故障28 组进行测试，测试结果如图10 所示。不同故障类型下的区内外故障测试样本为第1～18个，故障情况设置见表2；不同过渡电阻下的区内外故障测试样本为第19～34 个，故障情况设置见表3；不同故障初始角下区内外故障测试样本为第35～54个，故障情况设置见表4。为了方便对不同区内外故障类型进行阐述，L1、L2线路分别用1、2 来表示，接地故障用G表示。

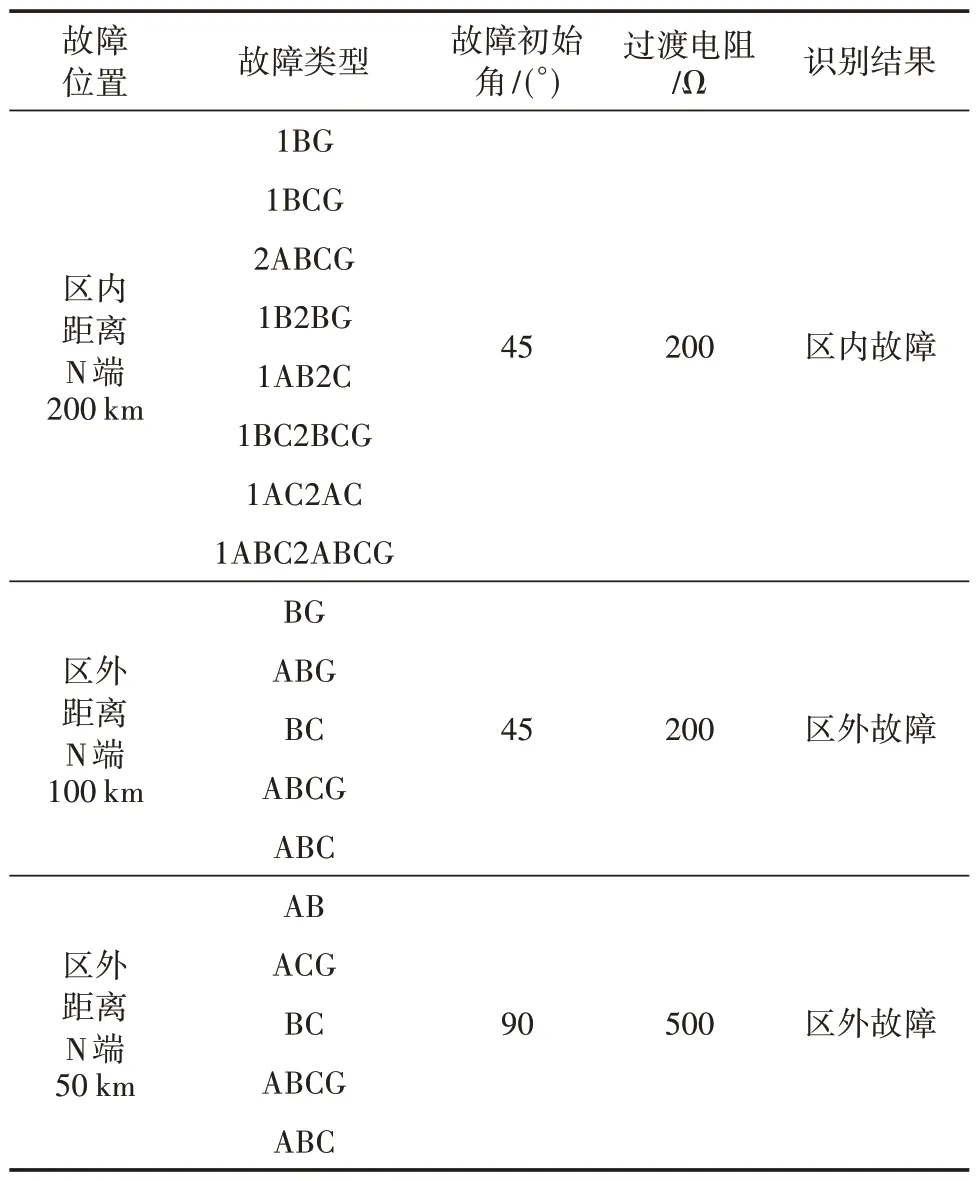
表2 不同故障类型下测试结果预测

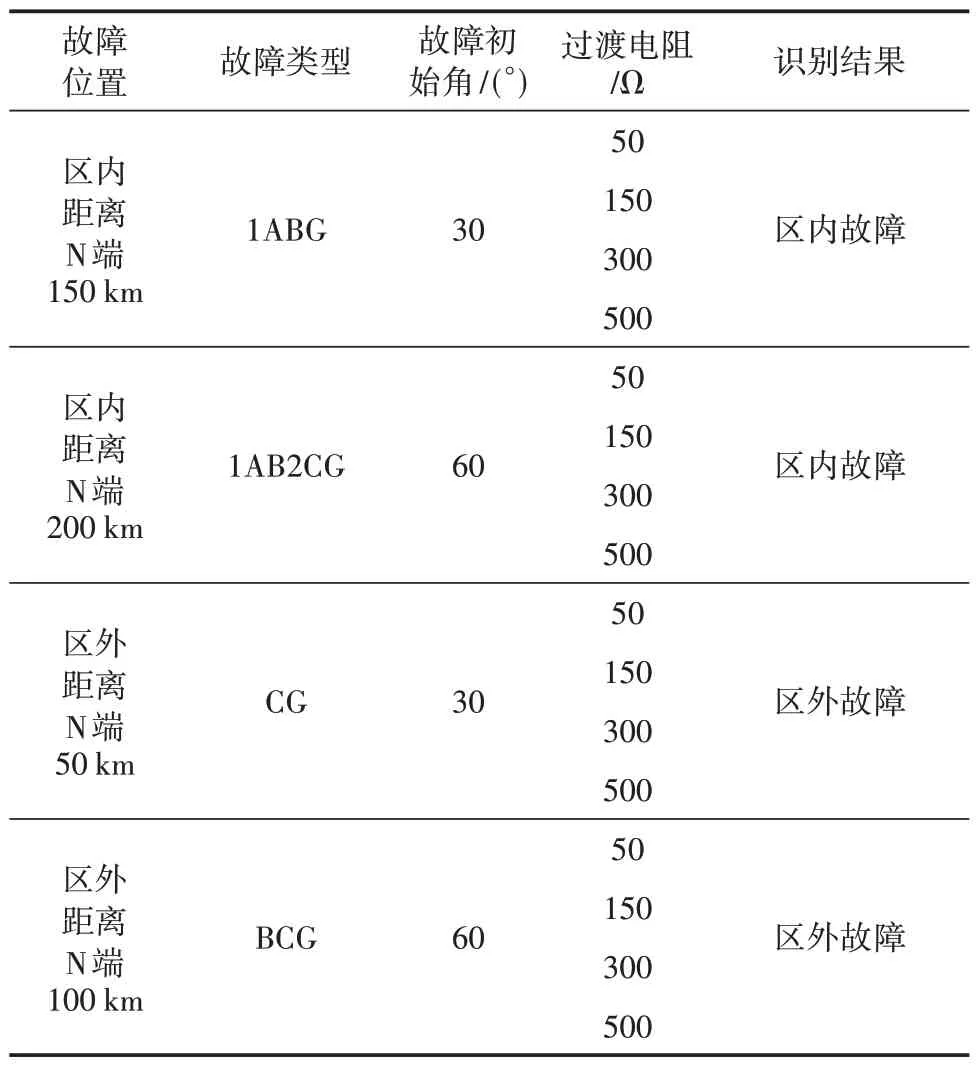
表3 不同过渡电阻下测试结果预测

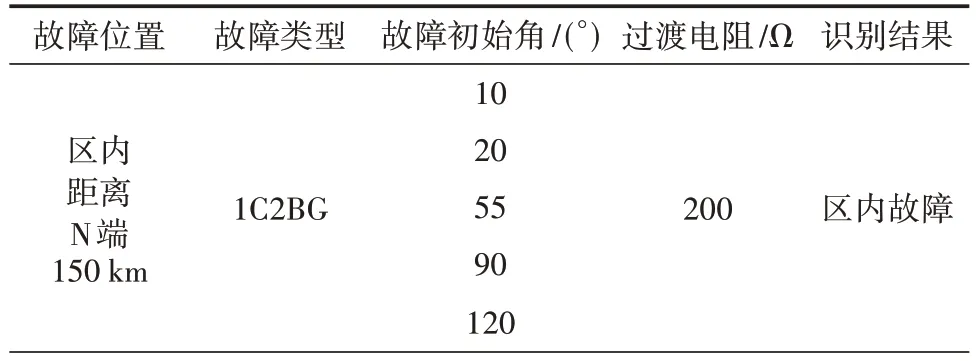
表4 不同故障初始角下测试结果预测

图10 测试集测试结果

由表2、表3 和表4 识别结果可知，算法不受故障类型、过渡电阻以及故障初始角的影响。

4.4 算法性能分析

4.4.1 抗CT饱和

为了测试模型在CT饱和下算法识别效果，以M端饱和进行实验，采集故障样本进行测试，测试结果见表5。从表5 中可以看出该算法具有一定的抗CT饱和能力。

表5 抗CT饱和测试结果

4.4.2 抗噪干扰能力分析

为了测试算法抗噪能力，分别选取不同的故障样本进行测试，预测结果见表6。

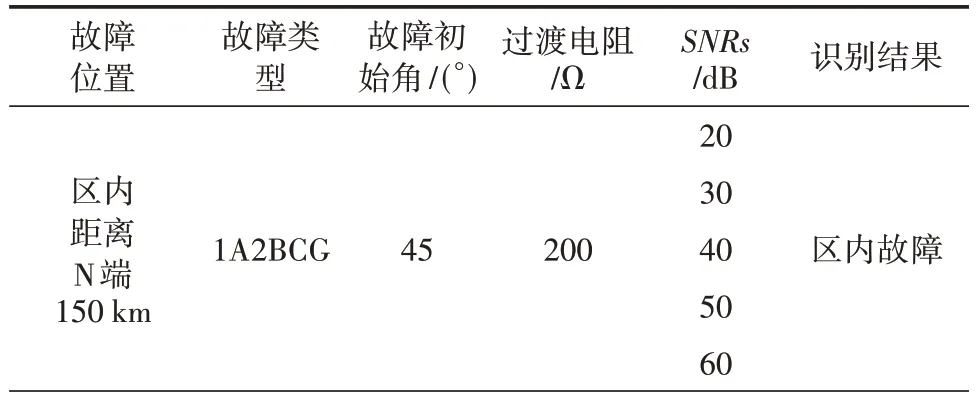
表6 噪声干扰下测试结果

表6 可以看出，在信噪比为20 dB 时，区外故障不能正常识别；在信噪比为30 dB 以上时，文中的方法能正常识别区内外故障，具有较强的抗噪能力。

4.4.3 不同故障位置测试

为了测试算法对不同故障位置的识别效果，选取不同的故障样本进行测试，测试结果见表7。表7结果表明该算法不受故障位置影响，能够有效保护线路。

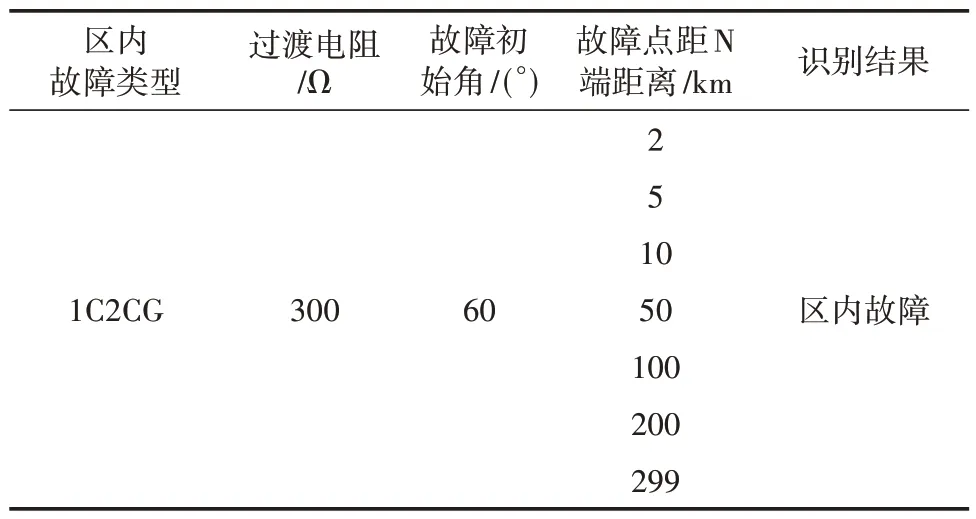
表7 不同故障位置下测试结果

4.5 算法对比

为了验证本文算法的识别效果，选取其他4 种网络（BP、RF、Softmax 和ELM）与本文的DE-ELM 网络进行对比，结果见表8。差分进化算法优化极限学习机的准确率相比其他4个网络算法在不同样本种类下准确率更高。

表8 不同网络模型对不同样本种类识别结果 %

5 结束语

通过对区内外故障后一段时间窗内电压反行波波形特征进行分析，提出了一种基于VMD+DEELM 同杆双回输电线路故障识别算法。通过理论与仿真分析得到以下结论：

1）当发生区外故障时，在[τ,2τ)时窗内其中一端保护单元检测不到反行波信号，两端反行波电压分解后能量分布不均匀，且两端对应尺度下模态分量的能量熵相差较大。

2）当发生区内故障时，在[τ,2τ)时窗内两端保护单元都能检测到反行波信号，两端反行波电压分解后能量分布较均匀，且两端对应尺度下模态分量的能量熵相差不大。

3）在CT 饱和、噪声干扰情况下，基于VMD+DE-ELM 同杆双回输电线路故障识别算法能够正常识别出区内外故障，算法可靠性和稳定性较好。