基于深度学习的电容式电压互感器故障诊断

黄桂平，吴 杰，夏 岩，熊兴中，张 蕊

(1.四川轻化工大学自动化与信息工程学院，四川 宜宾 644000； 2.智能电网四川省重点实验室，四川大学、国网四川省电力公司，成都 610000； 3.国网四川省电力公司电力科学研究院，成都 610000；4.人工智能四川省重点实验室，四川 宜宾 644000）

引 言

近年来，国家大力支持传统变电站向智能化和数字化方向发展。因此，智能变电站应具有先进的检测技术作为支撑，确保变电站能可靠、高效、经济、安全地运行。电容式电压互感器（CVT）因占地空间小、成本低廉、可靠性高、易维护等特点，优于传统的电磁式互感器，主要被用在35 kV 及其以上电压等级的变电站中，在高压变电站中起到不可替代的作用。CVT 主体结构由电感和电容构成，由于CVT 结构的特殊性，内部电容击穿故障也时有发生，为变电站的可靠运行带来巨大的挑战，如何实现CVT 的实时故障分类与故障预警是当前需要迫切解决的问题。

目前国内外对CVT 的研究主要集中在稳定性分析、测量精度提升、谐波抑制等方面。文献[1]采用虚拟阻抗补偿，消除了暂降电压误差的多样性，实现CVT 的暂态误差矫正。文献[2]采用迭代加权的Back Propagation（BP）网络对CVT 变比特性进行拟合，实现简单的故障识别功能。文献[3]采用滑动时窗K-Means 聚类法实现了互感器的故障诊断，但未能实现故障的实时预测。文献[4]采用小波变换理论实现故障的检测，利用Kullback 信息系统的数值变化与设定的阈值进行对比，实现了故障的检出，但未作出故障的预测设计。文献[5]将BP 神经网络与设备中的谐波结合，搭建新型网络模型提取互感器故障信号特征，实现了CVT 故障分类功能，但未作出故障实时检测。文献[6]研究互感器的故障类型，并使用传统的集成前馈神经网络（Feedforward Neural Network，FNN）进行样本训练，实现了互感器的故障诊断分类，但未设计故障的预测功能。文献[7]研究CVT 击穿时的小波基函数，利用小波三尺度重构的方法辨识故障信息，实现了CVT 故障分类。目前关于CVT 实时故障预警分类的研究还较少，以上研究均有不同程度地涉及到CVT 实时故障检测和分类，但都未考虑到CVT 的故障检出速率与精度性能指标。

综合上述研究与分析，本文对传统的卷积模型进行改进，提出一种M1DCNN 模型，将所提模型与其他模型进行对比实验，比较其故障分类精度，同时对M1DCNN 模型应用于CVT 故障在线检定的可靠性与实时故障预警功能进行研究。

1 理论背景

1.1 CVT工作原理

电容式电压互感器（CVT）通常运用于35 kV 及其更高电压等级的变电站中，可以实现将载波频率耦合到输电线用于长途通信、远方测量、选择性线路高频保护等功能。电气原理图如图1 所示，主体结构可以划分为分压单元与电磁单元两部分，其中分压单元由高压电容C1与低压电容C2串接组成，电磁单元由降压变压器、补偿电抗器、避雷器等器件组成。设定母线电压为U1，串接分压后得到分压电压U2，U2接入降压变压器降压后输出二次电压。

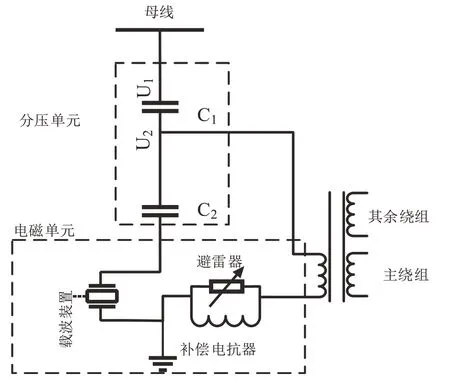
图1 CVT电气原理图

分压电容由多个电容串接构成，CVT 正常工作时，单个电容一般分压1 kV 左右，且能承受3～6 kV的冲击电压。从CVT 的结构分析，分压电容分成高压电容和低压电容两部分，当高压电容出现击穿时，平均分配到串接电容的电压也增加，更容易使余下的电容再次被击穿，直接影响CVT 二次侧输出电压。当二次侧并联继电保护装置时，由于CVT 因故障导致的测量误差，会使继电保护装置误动作迅速切断刀闸，给变电站的稳定运行带来威胁。

1.2 卷积神经网络

本文运用卷积网络实现采样数据信息的特征提取，经典卷积神经网络（CNN）如图2 所示，图中所示的网络结构仅能处理二维数据，对于本文的一维电压数据，若将一维数据转换为二维数据，将导致数据失去与时间的相关性，故不采用该网络结构。由于训练数据集数量过多，需要对传统的CNN 进行相关改进。首先对网络最后一层卷积增加平均池化层，对训练参数集进行降采样，保留数据集背景信息，节约计算空间。每层卷积运算的激活函数均使用ReLU，防止模型过度拟合，全连接层采用SVM代替传统的softmax实现故障的分类。

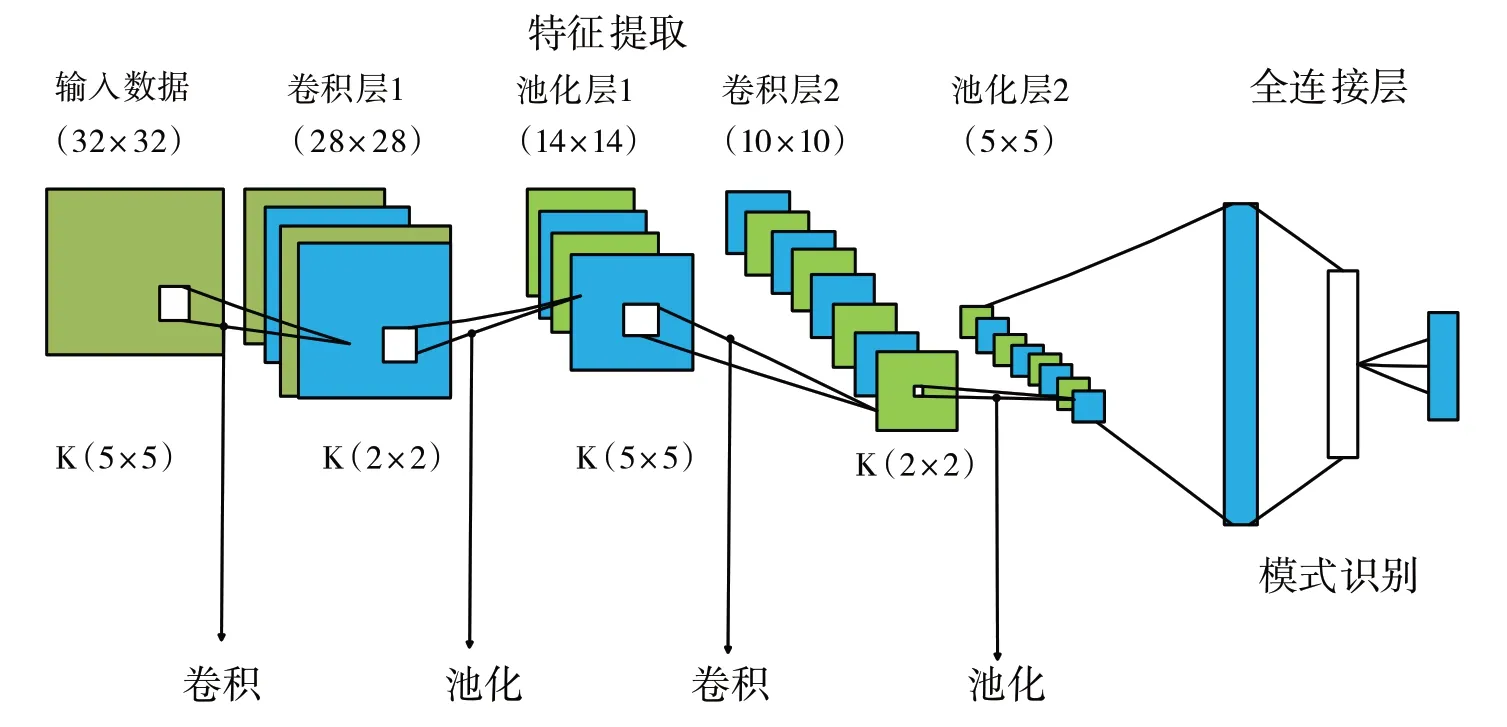
图2 CNN分类模型图

本文中的CVT 二次输出电压是一维时间序列信号，具有强烈的时间相关性。如用常规的方式直接将一维信号转换为高维度的信号，会破坏原始信号的时间相关性，不利于对故障信号进行卷积运算与故障特征提取，故选取一维卷积神经网络（1DCNN）用于本文故障分类器设计[8]。

一维卷积模型分类阶段由多层感知器组成，其前馈计算过程如式（1）所示：

其中X=[X1,X2,…,Xn]∈R1×m作为特征值，输入的数据为CVT 在线检定系统中的电压信号，m为样本长度；f1,f2,…,fN为每一阶段的线性或非线性运算；θ(1),θ(2),…,θ(N)为网络模型的训练参数集，f(X)作为输出。

卷积层作为卷积网络运算的重要组成部分，运算原理图与计算方法如图3所示。

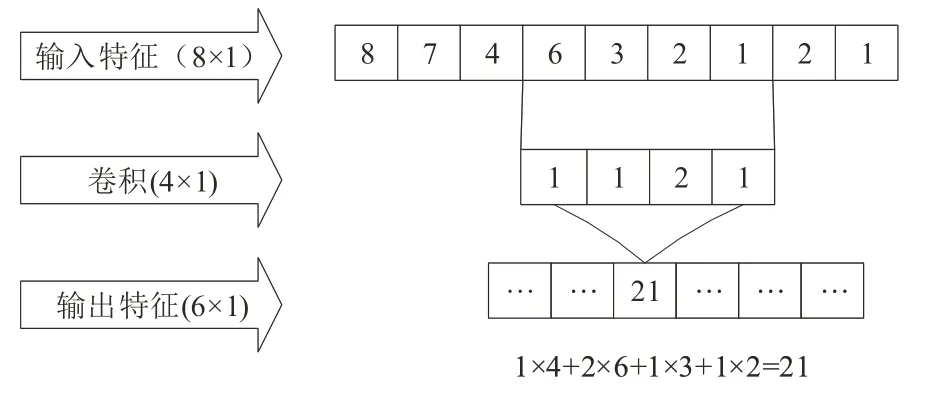
图3 SVM分类模型图

在图3 所示的卷积运算图中，卷积核与输出重合的部分以斜对角相乘并求和的方式，给出一定的偏置。该卷积运算可用式（2）描述：

其中，i为网络层索引；k为第k个输出特征图；Bki为第i个卷积层的第k个卷积核偏置，k=1，2，…，K；c为输入特征图通道图，c=1，2，…C；W ic,k为第i个卷积层c通道第k个卷积核的权值。

使用激活函数增强网络模型的拟合度，提高网络模型的收敛速度以解决非线性模型的问题，将卷积运算公式加入激活函数后，卷积运算可以用式（3）描述：

常用的激活函数主要有3 种：Sigmoid、tanh 和ReLU。其中Sigmoid 输入值定义域为(-∞, + ∞)，值域介于(0,1)之间，其优点是逻辑更为接近生物的神经元，即使输入的数据变化非常大其输出也非常平缓，即梯度消失；tanh在实际的使用过程中在一定程度上缓解了Sigmoid出现梯度消失的情况，但是针对梯度较明显的数据集仍会出现梯度消失，不适用于梯度性较强的数据集训练；ReLU 相比较于tanh、Sigmoid 能有效防止梯度消失，因此传统的CNN 大多都使用ReLU 作为激活函数，用以弥补其余两种激活函数的缺点。本文实验对数据集的背景信息较为敏感，最后一层卷积输出层设计采用如图4 所示的平均池化，最大限度保留数据集的背景信息，更有利于网络模型完整表达故障信息。在传统的CNN中，其最大池化运算的如式（4）所示：

图4 平均池化与最大池化

其中A(ik)(tx)表示第i个卷积层的第k个输出特征图中的第tx个像素值。S为池化窗长度，{A(ik)(tx)} 是形状为S× 1的矩阵，p(ik)为输出特征图。

全连接层可用式（5）描述：

在传统的CNN 中，全连接层的参数数量占整个网络总数的80%以上。全连接层分布着众多的训练参数，在训练过程中会占用过高的计算空间。随着全连接层层数的增加，相关的参数也会成倍增加，直接影响到计算速率与计算精度。此外全连接层层数过多会导致模型过度拟合，与本文改进的卷积网络有一定的冲突。使用传统全连接层的一维卷积模型用作CVT 故障在线诊断时，运算时间剧增，偏离了实验设计的初衷（快速性、高精度），因此传统的全连接层并不适用于本文的故障诊断与故障在线检定设计。本文的实验设计中，处理的是一维时间序列信号，对数据集维度与深度特征提取的要求不高，当使用传统的softmax 作为全连接层时，故障分类时间长，分类精度低，不能满足快速检出故障的要求；当使用SVM 作为分类器时，模型分类精度得到提高，分类所耗时间也比使用softmax 少，因此SVM更适用于本文的模型。

2 基于M1DCNN-SVM故障诊断算法

2.1 改进的1维CNN（MIDCNN）

本文对传统卷积神经网络结构进行改进，改进的1DCNN-SVM 模型（MIDCNN）结构如图5所示，从图5 中可以看出，模型有3 个主要的部分构成，包括卷积层1、卷积层2、平均池化层，两层卷积分别对输入数据进行特征提取。为了降低网络模型的训练参量，最后一层卷积输出层使用平均池化层来代替全连接层，减少训练参数总量的同时，极大程度地保留异常电压信号的特征信息，平均池化表达式如式（6）所示：

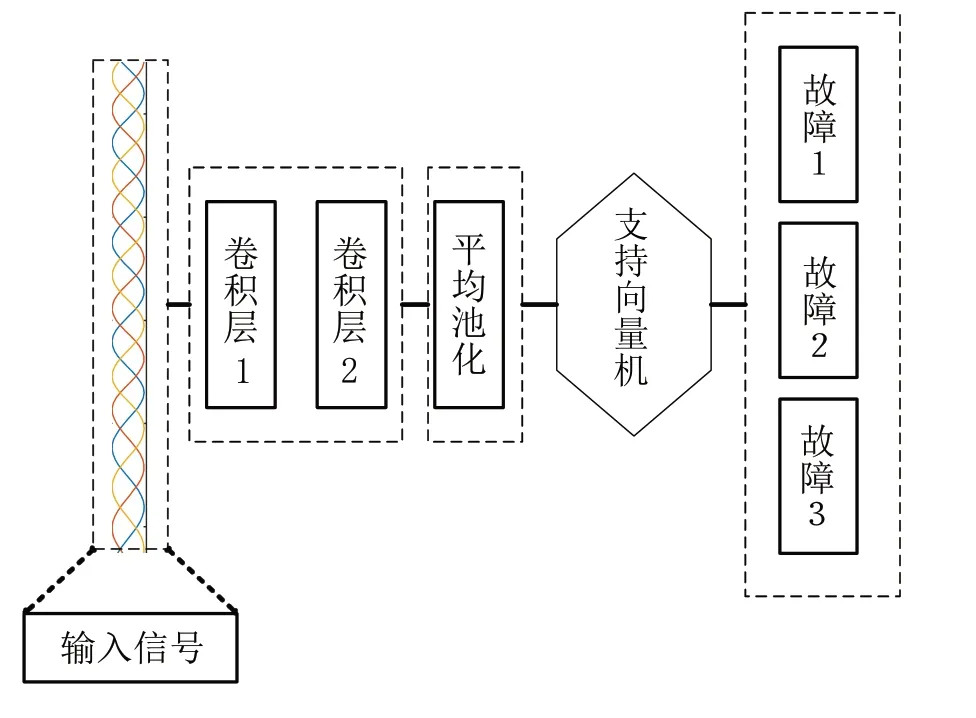
图5 M1DCNN-SVM模型

本文仿真模型由4 种运行工况构成，其中故障工况由高压电容故障、低压电容故障、电磁部分故障3 种类型构成，实际上是一个3 分类问题，输出维度为3，输出特征图为1×1×3，由于输入端通道与输出端的通道不兼容，应设计一个卷积层将n维数据集转换成1×1×3的输出。卷积层各项参数按首字母排序，改进卷积模型的详细参数见表1。

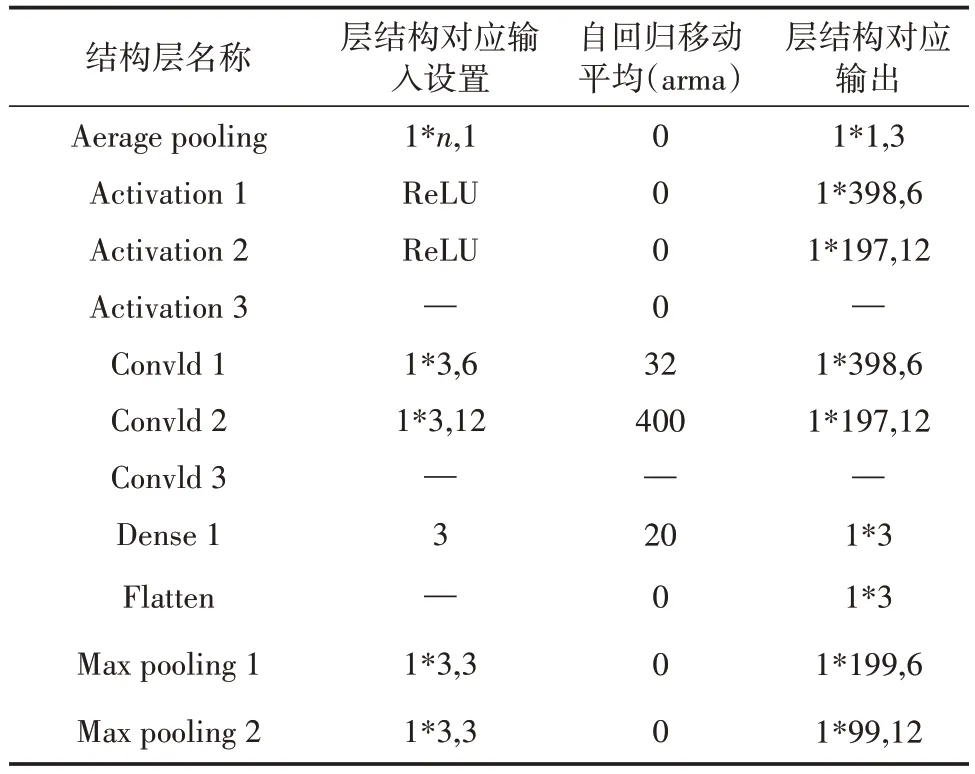
表1 CNN参数分布

2.2 故障模型与诊断算法

CVT 的工作原理是通过调节串联高压电容与低压电容的容值比例，分配母线电压，再经过中间变压器降压后接入测量表计，实现母线电压的测量。由于CVT 的分压是由大量的电容串接分压实现的，因此分压电容被击穿导致的CVT 二次电压异常的故障也频频发生。例如当高压电容被击穿，CVT 二次侧电压升高导致继电保护误动作跳闸，影响电网稳定运行， CVT 电路简化结构[8]如图6所示：

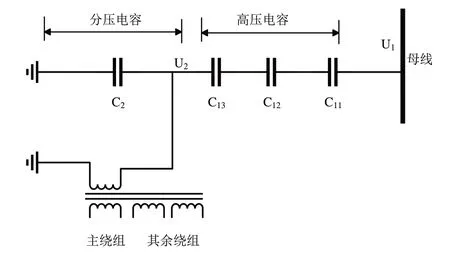
图6 CVT电路简化结构图

在图6 所示的CVT 电路简化图中，母线电压U2经过电容分压后得到电压U1，如式（7）所示：

因此，CVT 电容分压比可以用式（8）表示：

其中，n1为串联电容C1的个数，n2为串联电容C2的个数。当C1中击穿n1x个电容后，CVT 的分压比如式（9）所示：

因此由式(8)与式(9)得出互感器二次输出电压的变化率如式（10）所示：

同理可得C2被击穿后，互感器二次输出电压的变化率如式（11）所示：

结合上述公式，对应母线额定电压为500 kV 的二次侧电压变化率见表2。

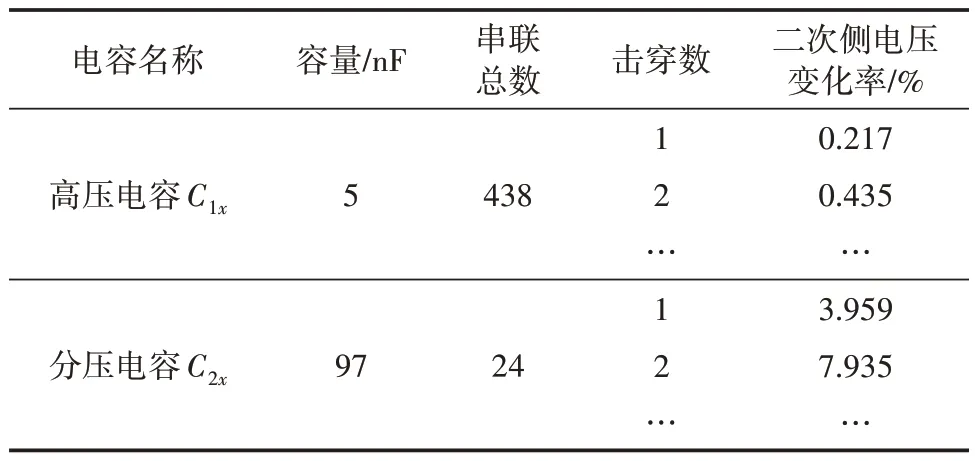
表2 电容击穿与二次电压关系

研究电容击穿数量和击穿种类对二次电压的影响，列出以下几种故障数学模型，以区分 CVT 不同工况的故障[9]。常见 CVT 故障类型与二次电压变化关系见表3。

表3 故障模式和数学模型

由表3 的CVT 数学模型可知，本文主要为3 分类故障。考虑电网电压处于稳态，特定的电容故障会导致母线电压发生表2列出的规律变化。不同功能的电容故障都代表不同的故障类型，通过二次侧输出电压的变化逆向推理CVT 的故障状态，并且根据电压的变化幅度推理故障类型与故障程度，从而实现故障预测与故障分类。

3 算例分析

3.1 仿真系统与数据集

3.1.1 仿真系统

在Matlab 搭建如图7 所示的仿真模型，CVT 的高压电容容量为5 nF；低压电容容值为97.06 nF，仿真时长为500 ms，步长为50 μs。仿真模型中CVT二次侧电压波形如图8 所示，其中正常电压表示CVT工作在稳态过程，采集到的二次端口电压为正常值，如图8 曲线a。模拟系统低压电容被击穿，当模拟低压电容被击穿数为1 个时，低压电容串接部分的容值增加，采集到二次侧输出电压波形如图8 曲线b。模拟系统高压电容被击穿，当模拟高压电容被击穿数为1个时，高压电容串接部分的容值增加，采集到二次侧输出电压波形如图8 曲线c。从图8中可以看出，不同类型的电容故障对应的故障类型不同，并且故障类型非常容易区分。

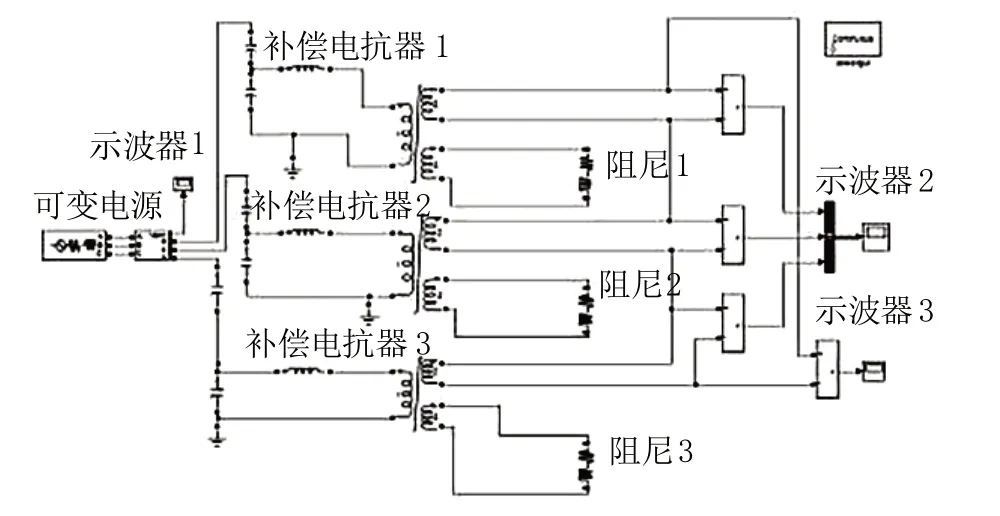
图7 MATLAB仿真模型

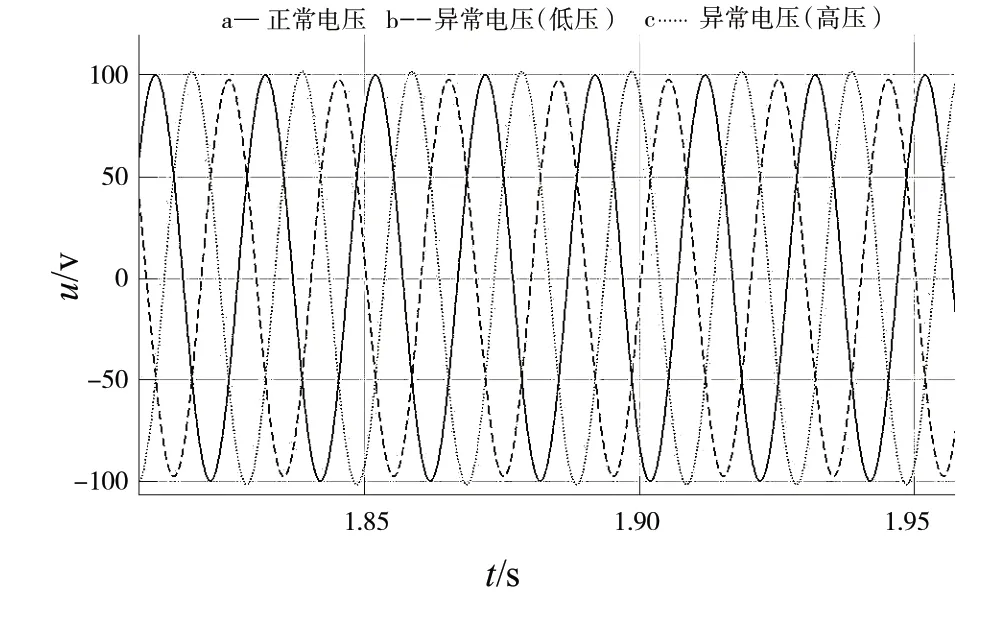
图8 CVT二次侧电压波形

3.1.2 数据集

针对电力时空运行冗余数据多，类型复杂的问题，采用模态分解法对变电站报送的CVT 电压数据去噪，采用滑窗分割法对采集的电压信息进行规范化处理[10]，为CVT 故障诊断和运行趋势预测提供可靠的训练集和测试集。仿真试验数据来自某变电站CVT 实测电压数据，通过采集4 种不同工况下电压数据，参考仿真模型的电压数据建立CVT 数学模型。CVT 工作参数为：额定一次电压等级为300 kV，额定二次电压等级为100 V，高压电容容值为5 nF，低压电容容值为97.06 nF，设置电压信号采集器的工作频率为50 Hz，数据表部分数据见表4。

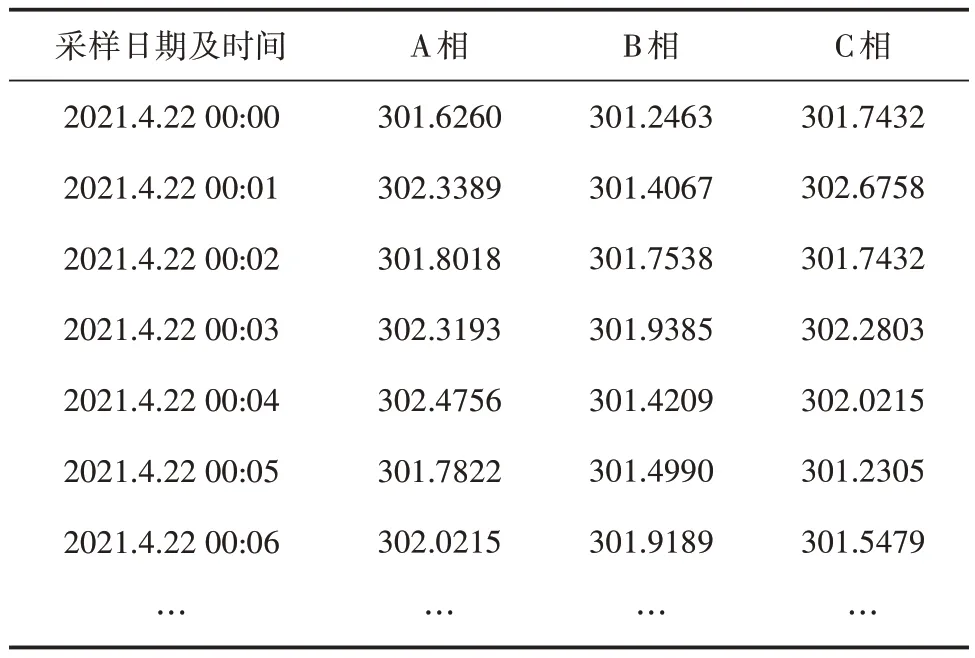
表4 电压数据集 kV

由几种常见电压波形（见图8）可知，不同故障下的电压波形有明显的区分度，电压波形与表3 的数学模型相符，表明本文建立的数学模型与实际相吻合。本文的数据集由3 种故障类型与1 种正常数据构成，总共采集到483 840 个数据，将采集到的电压数据划分为96个样本空间，每种故障类型对应24个样本空间，每个样本空间包含5040个采样点。数据标签1、2、3、4 分别代表正常、低压电容部分击穿/匝间短路、高压电容击穿、电磁断线/低压电容全部击穿4 类工况，训练集和测试的划分按2∶1 分配，相关信息见表5。

表5 故障数据集描述

3.2 实验结果与分析

本文通过以上理论，完成数据集划分与数学模型的搭建，在传统的CNN 分类模型中做出改进[11]，建立一维卷积平均池化模型（M1DCNN）。为了验证本文所提的方法与其他方法差异，对不同网络层的参数进行数量总和分析，对比分析相关参数见表6。由表6 可知，使用传统的1DCNN 实验，所有参数总和为452 220 个，对传统的1DCNN 网络进行相关改进，加入平均池化层和SVM 后，所有网络训练参数仅为452 个。本文改进的网络相比于传统的1DCNN 网络，极大程度上降低训练参数，节约了存储空间[12]。

表6 训练参数总量对比

在对比实验中，将参与实验的网络模型卷积层都使用ReLU、Sigmoid、tanh 作为激活函数，分别做5组实验，每组实验的模型训练迭代次数均为40，分别实验5 次，计算3 种激活函数下测试精度、测试时间、训练时间的平均值，对比实验诊断结果见表7～9。

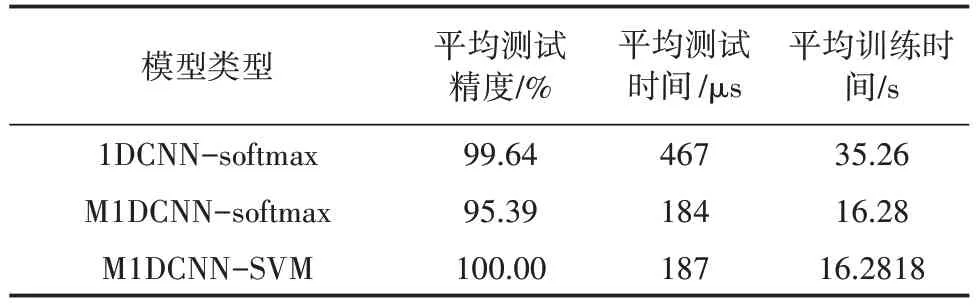
表7 ReLU实验精度对照表

使用ReLU 作为激活函数，计算平均训练时间过程包含两个阶段，一部分是模型训练阶段，另一部分是模型测试阶段，最终的平均训练时间为这两部分的总和。由表7 可知，本文所提的方法测试精度为100.00%。测试时间方面，本文方法只用了187 μs，比 上 述 的 1DCNN-Softmax 更 快，与M1DCNN-Softmax 接近；由表7 可知1DCNN-Softmax训练时间为35.26 s，M1DCNN-Softmax 训练时间为16.28 s，SVM 训练时间为0.0018 s，因此可以计算出M1DCNN-SVM 总训练时长为16.2818 s。比较分析结果可知，M1DCNN-SVM 在综合性能上比1DCNNSoftmax、M1DCNN-Softmax 更具优势，网络训练参数得到优化，提高了网络的诊断精度。

由表8 可知，使用tanh 作为激活函数，1DCNNSoftmax 的测试精度为91.31%，M1DCNN-Softmax 为90.35%，M1DCNN-SVM 为97.36%。比较分析结果可知，使用相同的tanh 做激活函数条件下，M1DCNN-SVM 在综合性能上也比1DCNN-Softmax、M1DCNN-Softmax更具优势。

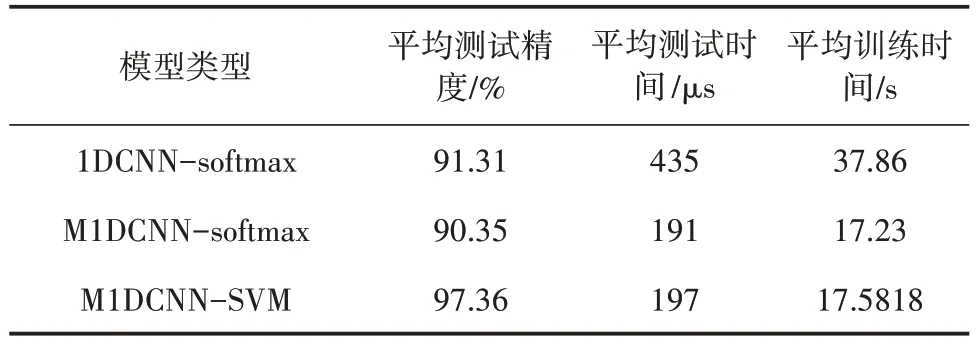
表8 tanh实验精度对照表

由表9 可知，使用Sigmoid 作为激活函数，1DCNN-Softmax 的测试精度为96.67%，M1DCNNSoftmax 为93.26%，M1DCNN-SVM 为98.39%，平均测试精度比表8 中使用tanh 激活函数更高，但测试时间都高于使用tanh用作激活函数的网络模型。

以上3 种对比实验表明，本文的实验设计中用ReLU 作激活函数时，1DCNN-SVM 模型具有良好的故障分类效果；相比较于使用tanh、Sigmoid，改进的网络模型在综合性能上表现更好，表明ReLU 更适用于本文的网络模型。

为了进一步验证ReLU 在本文改进模型的精确度与实用性，分别对深度信念网络（DBN）、SVM、M1DCNN-SVM 与KNN 4 分类网络进行对比实验[13-15]，均采用相同的数据集与实验平台，对每一种分类网络做5 次实验并求取各项指标的平均值，比较结果见表10。表10 展示了3 种传统的故障诊断方法与本文所提方法的对比实验，由表可知，KNN和DBN 的平均测试精度接近100%，DBN 的平均训练时间比M1DCNN-SVM 小，KNN 与之相近，说明这两种传统方法具有快学习的能力，测试精度与训练时间都有较好的性能。SVM 在训练时间上比KNN和DBN 更少，说明SVM 的网络结构更加简单，收敛速度最快，但精度只有90.35%，不满足本文设计要求。由表可知，M1DCNN-SVM 的测试精度为100.00%，训练时间相对于DBN 略有增加，考虑整体性能与精度要求，本文所提的方法更适用于CVT 的故障在线检定。

表10 实验精度对照表

4 结束语

本文将传统的一维卷积神经网络用于CVT 的故障诊断中，提出M1DCNN-SVM 故障诊断模型，用于CVT 故障在线检定与故障预测。本研究在最后一层卷积加入平均池化层，使用支持向量机代替传统的全连接层，使总参数降低为原有模型的0.100%。所提模型在结构上解决了传统CNN 运算困难、运算参量大、训练时间与测试时间长等问题。将改进的一维卷积模型与传统的一维卷积模型分类方法进行对比，结果表明本文所提的故障在线检定方法在分类精确度、训练时间、测试时间上都优于传统方法，且提高了故障模型的分类效率，加快了CVT 故障检出率，具有100%的故障检出精度，为高压变电站平稳运行提供了一种有效的方法。