基于遗传算法和集成剪枝的表情识别方法

唐玉梅，李丹杨，何 庆

（贵州大学大数据与信息工程学院，贵阳 550025）

引 言

面部表情识别是模式识别与人工智能领域的研究热点，在医疗[1]、教育[2]等领域有着广泛的应用。尽管已有学者对表情识别技术展开一系列的研究，但由于年龄、性别等综合因素的影响，要达到较高的表情识别率仍然富有挑战性[3-4]。

深度学习能有效提升表情识别效果，Li等[5]提出了一种注意力机制的卷积神经网络模型识别表情；Ge 等[6]提出一种基于深度学习的表情识别方法。但是，这些方法均采用单个分类器进行分类预测，对未知数据的预测能力有限。

集成学习通过组合若干分类器，提高模型的泛化能力[7-8]，可有效弥补单一模型在表情识别领域的不足。然而，随着集成分类器数目的增多，一方面计算量和需要的存储空间急剧增大；另一方面出现较多冗余分类器，降低预测系统的识别效果。

集成剪枝从基分类器池中选择部分多样性较好、预测准确率较高的分类器集成，在实现提高集成系统泛化能力和预测性能的同时，保证了模型预测的实时性[9-10]。基分类器的准确率与多样性是影响集成剪枝效果的两个重要因素，但二者又处于矛盾关系。搜索平衡了准确率和多样性的最优子集有助于构建可靠性高的分类系统。使用元启发式算法选择分类器，能够在可接受的计算成本内尽可能搜寻最优解。Zhu 等[11]提出了一种改进的离散人工鱼群算法与边缘聚类最小化相结合的集成剪枝方法；Peng等[12]提出一种针对复杂工程优化问题的选择性集成多策略萤火虫方法，设置了3 种不同的搜索策略。

上述方法收敛速度较慢，勘探和开发之间没有得到很好的平衡，容易陷入局部最优。遗传算法具有隐含并行性和全局搜索两大显著特征[13]，在机器学习、组合优化和图像处理等领域得到广泛的应用[14-15]。综上，本文提出一种基于遗传算法和集成剪枝的人脸表情识别方法。首先，使用卷积神经网络构建基分类器；其次，通过遗传算法剔除冗余分类器和弱分类器；最后，将剩余分类器按准确率降序排序，并依次逐个加入集成系统，进行大多数投票法集成，直到达到最高的表情识别率。和多种剪枝方法相比，本文提出的基于遗传算法和集成剪枝的表情识别方法贡献如下：

1）提出一种用于集成剪枝的混合初始化种群方法，该方法通过二进制编码和自然数编码分别生成等量的初始种群，既增加种群的多样性，也加快收敛速度。

2）提出一种启发式信息引导的类似路径构造的初始化种群方法，该方法使用自然数编码，根据分类器之间的准确率和多样性关系引导初始化种群生成。

3）使用自适应变异和交叉算子改进了遗传算法的遗传进化过程；构建了一种简单有效的适应度评估函数，以提高算法的收敛速度和精度，减少集成系统的分类器规模，提高表情识别的效果。

1 基于遗传算法和集成剪枝的表情识别方法

本文提出一种基于遗传算法和集成剪枝的表情方法，以有效提升人脸表情的识别效果。所提方法主要包括3 个部分：首先，使用卷积神经网络生成若干分类器，形成基分类器池；其次，使用遗传算法对分类器池中的分类器进行选择，得到最优分类器子集，并按照准确率降序排序；最后，选择前n个准确率最高的分类器子集进行大多数投票法集成，得到最终的决策结果。具体流程如图1所示。

图1 基于遗传算法和集成剪枝的表情识别方法流程图

1.1 基分类器训练

卷积神经网络(CNN)可以更好地展现图像的深层次信息，对大型图像处理表现十分出色。因此，本文选择卷积神经网络（图2）作为基分类器，拟合表情数据，进行基分类器池的构建。

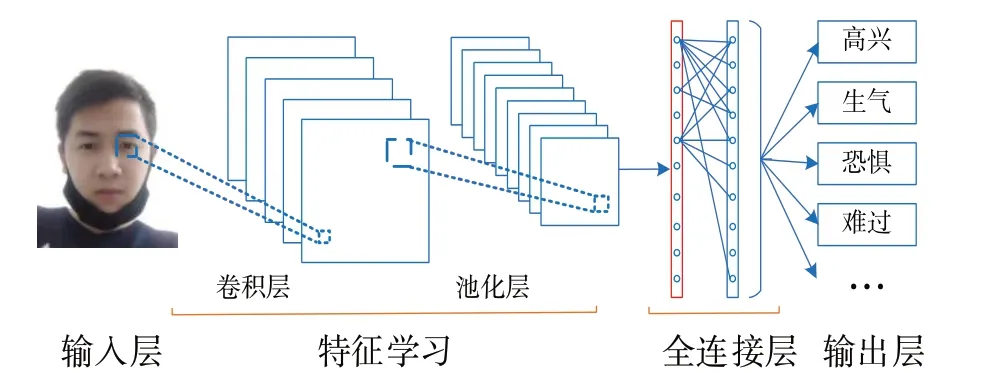
图2 卷积神经网络模型

1.2 基于遗传算法的分类器选择模型

1.2.1 “二进制+自然数”编码

为了适应本文提出的初始化方法，使用混合编码的方式。由于自然数编码适用于次序的组合优化问题，二进制编码操作简单易行，基本的选择、交叉和变异等遗传操作易于实现，因此，初始化阶段使用自然数与二进制编码。自然数编码只用于种群初始化阶段，给每个分类器分配一个编号，按编号确定分类器的组合顺序。后续的遗传操作均选择0、1 二进制数值作为编码方案（见图3），染色体是一个位符串，长度等于基分类器池中分类器的总量，染色体上的基因值1 代表对应编号的分类器被选择，其余分类器不参与最终的决策层集成，则图3 中染色体表示共有8个分类器，其中第1、5、7个分类器被选择参与集成。

图3 染色体示例

1.2.2 “随机+启发式信息引导”的初始化种群方法

进化算法中，初始种群通常是随机生成的，会导致种群陷入局部最优。本文通过两种方法生成初始种群：一种是随机初始化；另一种是启发式信息引导的类似路径构造的初始化方法。两种方法结合，能够在保持种群多样性的同时，加快遗传算法的收敛速度。

设G={C,E}为一个有向全连通图，其中C=(c1,c2,…,cD)为D个基分类器组成的集合，表示图的节点，E={ (ci,cj):ci,cj∈C}表示图的边，边的权重计算方法为：

其中，Acc(ci)为分类器ci的预测准确率;d(ci,cj)为两个分类器之间的相似性，使用汉明距离作为度量准则，如式（2）所示；MI(ci;L)为分类器与实际预测标签之间的相关性，如式（3）所示。

其中，⊕为布尔运算中的逻辑“或”运算，|·| 为基底。设有n个验证样本，则分类器c可以表示为c=(pre1,pre2,…,pren)，prei表示分类器c对第i个样本的预测结果；L=(l1,l2,…,ln)表示样本的实际标签向量，lj表示第j个样本的实际标签，则分类器c与实际标签L之间的相关性为：

其中，p(prei,lj)为联合概率分布，p(prei)和p(lj)分别为c和L的边缘概率分布。相关性值越大，表示分类器预测结果越可靠。

启发式信息引导的类似路径构造的初始化种群方法步骤如下：

1）使用自然数编码方式给每个分类器分配一个编号，将分类器之间的关系视为无向全连通图，根据式(1)初始化各条边的信息强度及各分类器的禁忌表；

2）随机生成所有分类器的初始排序，并取前m个分类器作为m条路径的起点，按步骤3）构造m条不同路径；

3）分别在禁忌表的制约下，遍历剩余未选择的分类器，根据式（1）计算各条边的权重，选择与当前分类器权重最小的顶点作为下一个分类器，直到所有分类器都被选择，即按照分类器选择顺序形成m条完整路径；

4）分别选择各条路径的前n个集成准确率最高的分类器，并将对应编号位置的值设为1，得到选择分类器的二进制编码。

D= 8（即分类器池中包含8 个基分类器）时的集成剪枝初始化方法示例如图4所示。

图4 8个分类器的启发式信息引导的初始化种群示例

图4 中每条染色体代表一组分类器选择方案，染色体1 表示选择前5 个分类器集成能够使系统达到最高识别率，对应的分类器编号分别为3、5、1、6、7，转化为二进制编码时，将染色体第3、5、1、6、7 号基因值设为1，其余基因值为0。

1.2.3 基于互信息的适应度函数

互信息通常被用于衡量任意两个随机变量之间的相关性和统计依赖性，因此，本文使用一种简单有效的适应度函数实现分类器的选择，使得所选择的分类器与实际标签之间的平均相关性较大，且选择的分类器数量较少的染色体具有更高的适应度，如式（4）所示：

其中，α、β为平均相关性和选择分类器数量之间的权重因子，C=(c1,c2,…,cD)(ci∈{ 0,1 },1 ≤i≤D)为D个分类器集合的一组选择方案，{ 0,1 }为逻辑值，ci=1 表示分类器ci被选择，num(C)表示选择的分类器数量，corravg表示选择的分类器子集与实际标签的平均相关性：

分类器c可以用该分类器在n个验证样本上的预测结果向量表示，即c=(pre1,pre2,…,pren)，L=(l1,l2,…,ln)表示n个验证样本的实际标签向量，则分类器c与实际标签L之间的互信息为：

其中，H(L)为熵，表示L的不确定测度，可表示为：

H(L|c)为条件熵，表示在c已知时，L的不确定测度，可表示为：

综合式（6）～(8)可得最终分类器与实际标签之间的互信息计算公式为：

1.2.4 精英策略下的复合选择算子

轮盘赌轮选择策略具有简单、易操作、收敛速度快等优点。但是，当问题规模较大时，可能会出现最优解和次优解差异较大的现象，导致算法陷入早熟。本文使用混合轮盘赌轮和锦标赛选择算子，通过两种算子各选择一部分个体进入下一代，增加搜索的广度，一定程度保证适应度值较高的染色体被选择的机会更大，同时，有助于提高收敛速度。最后，选择精英保留策略，保留每一代种群中的最优个体，保证算法的全局收敛。

1.2.5 动态自适应交叉和变异概率

算法收敛速度使用动态自适应交叉概率pc和变异概率pm进行调整：当适应度值大于平均适应度时，减小pc增大pm，保持种群多样性，避免出现“早熟”；反之，则提高交叉概率，减小变异概率，提高算法的收敛速度。根据适应度值动态自适应调整交叉和变异概率，使得种群中优秀的个体不被破坏，又有利于新个体的生成，较大程度提高遗传算法的性能。设fmax为当前种群最大适应度值，f'为待交叉个体中较大的适应度值，f为待变异个体的适应度值，favr为种群的平均适应度值，则交叉概率为：

变异概率为：

1.3 分类器集成

使用大多数投票法将选出的分类器融合作为最终的预测类别mv(x)。输入测试样本x，大多数投票如式（12）所示：

其中，I(·)表示判别公式，L表示所有样本类别，ci(x)表示第i个分类器对测试样本x的预测标签。

1.4 基于遗传算法和集成剪枝的表情识别算法流程

1）输入表情图片，使用CNN 拟合训练集，构建基分类器池；

2）分别使用随机初始化和启发式信息引导的初始化方法生成等量的染色体，组合得到初始种群；

3）使用式（9）基于互信息的适应度函数评估个体的适应度，并找出适应度最高的个体；

4）判断是否达到遗传算法终止条件，是则执行步骤9）—步骤11），否则执行步骤5）—步骤8）；

5）通过轮盘赌盘和锦标赛复合选择算子选择参与交叉和变异的父代个体，直到达到原始种群的数量；

6）动态自适应交叉概率进行交叉操作；

7）动态自适应变异概率进行变异操作；

8）将步骤3）中找出的最优个体随机插入完成变异的种群，产生新种群；

9）输出最优个体；

10）将最优个体选择的分类器按准确率降序排序；

11）按照集成效果进行二次剪枝，依次增加分类器并使用式（12）进行大多数投票法集成，直至达到最优表情识别效果。

2 实验与分析

2.1 实验准备

2.1.1 数据集

实验选择FER2013[16]、JAFFE[17]、CK+[18]、RaFD[19]与KDEF[20]5 个经典的人脸表情数据集，并在所提出的基于遗传算法的集成剪枝框架上进行表情识别。各数据集部分表情示例如图5所示。

图5 各数据集表情示例

实验过程将所有表情统一成大小为48 × 48 的单通道图，并将数据集划分为训练集、测试集和验证集3 个部分。FER2013 训练集数据量较大，用作训练集训练分类器，获得模型参数；公共验证集用作验证集，验证分类器效果，进行模型参数微调；测试集包括FER2013 中的私有验证集（简记为FER）、CK+、JAFFE、RaFD 与KDEF，用于测试整个识别系统的性能。

2.1.2 评价指标

准确率（Accuracy，Acc）常作为衡量分类效果的标准。设TP和FP分别表示被正确分类和被错误分类的样本数量，Total表示总的样本数量，则Acc计算如式（13）所示：

2.1.3 训练细节

实验基于Tensorflow 框架，主要通过调整超参数、网络结构，共生成231个CNN 分类器形成分类器池。所更改的神经网络参数类型及范围见表1。

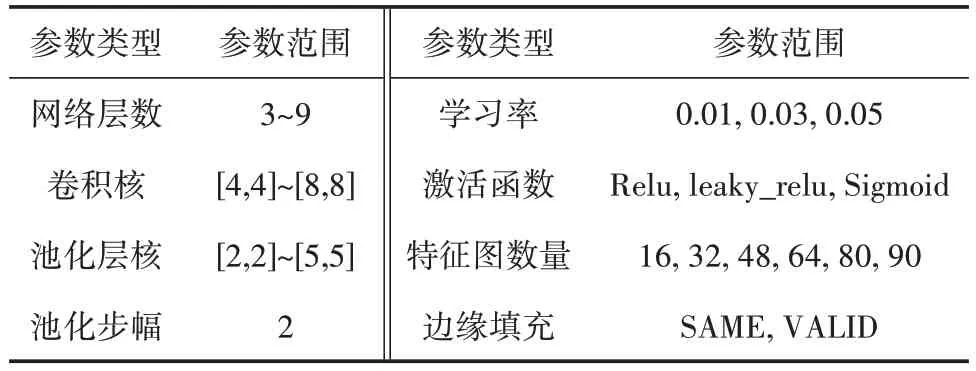
表1 卷积神经网络参数设置

生成的分类器对不同数据集的预测结果的箱线叠加散点图如图6 所示，清晰地展现了基分类器对不同数据集预测准确率的分布情况。箱线图由上至下各横线依次表示基分类器预测准确率的最大值、上四分位数、中位数、下四分位数和最小值。箱线图中处于最大值和最小值之外的数据视为异常值，说明该分类器预测效果不具有代表性。总体上，在各个数据集上的识别准确率较为分散，说明基分类器池具有较好的多样性。

图6 基分类器对不同数据集预测结果的箱线叠加散点图

2.2 实验结果与分析

实验设置最大迭代次数为300，锦标赛竞赛规模为5，平均相关性和选择分类器数量之间的权重因子α、β分别设置为0.9、0.1。在各个数据集上，对比不同种群规模pop对实验效果的影响，在各个数据集上的效果如图7所示。

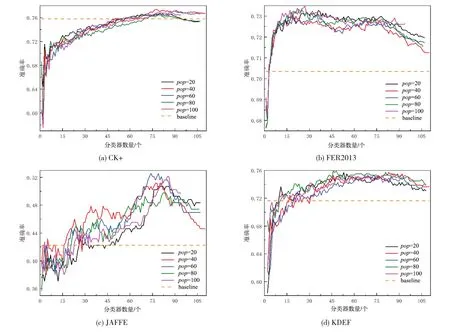
图7 不同种群规模下各个数据集上的集成剪枝效果

分类器池中共有231 个基分类器，通过遗传算法剪枝后，选出的分类器数量减少一半，再根据准确率进行二次剪枝，近一步缩小集成分类器的规模。图7 中，Baseline 为基线，表示所有分类器集成的效果，总体上，剪枝后的分类器集成效果优于将所有分类器集成。由于二次剪枝按照准确率降序排序，剪枝后系统的识别性能远远好于选出的效果最优的分类器。随着分类器数量的不断增加，各个数据集上识别准确率呈波动中上升又下降的趋势，这是因为不断增加分类器，后续分类器的识别效果较低，反而会降低整体的集成效果。相同条件下，各个数据集上不同种群规模的对比效果没有明显区别，说明不断增加种群规模不能从根本上找到最优解。

2.3 与其他方法比较

为了进一步验证所提方法的有效性，将本文方法与多个集成剪枝方法比较。表2 为经过多次实验，在各个数据集上不同算法的最佳效果，其中，baseline 为基线，表示将分类器池中所有分类器集成。从表2 可知，集成剪枝方法在各个数据集上的识别效果优于baseline，且具有比baseline 更小的分类器规模。与baseline 相比，本文方法在FER2013数据集上的准确率提高了3.01%，在JAFFE 上提高了9.96%，在CK+上提高了1.59%，在KDEF 上提高了4.70%，在RaFD 上提高了4.12%。和其他方法相比，总体上本文方法在各个数据集上都取得较高的识别准确率，并选择出较少的分类器，在RaFD 数据集上的集成剪枝效果优于大部分对比方法。

表2 不同方法在各个数据集上的剪枝效果对比

3 结束语

本文提出一种基于遗传算法和集成剪枝的表情识别方法。分类器选择过程中，使用改进的混合初始化策略能够生成多样化的初始种群；基于精英保存策略的轮盘赌和锦标赛复合选择算子，使用动态自适应交叉和变异概率进行遗传操作，保证迭代过程中种群多样性的同时，加快了算法的收敛速度。集成过程中，找出最优染色体对应的分类器子集，按照准确率降序排列进行二次剪枝，并使用大多数投票法集成得到最终预测结果。与其他集成剪枝方法在5 个经典表情数据集上进行对比，结果表明所提方法具有更优的有效性和显著性。集成剪枝效果一定程度上取决于基分类器的性能，因此，下一步工作将使用最先进的深度学习网络训练性能更高的基分类器，并使用最新进化算法进行剪枝，更好地提高表情识别的效果。