6005A铝合金的冲击动态本构模型及其有限元验证

盖凌锋，朱志武

（1.西南交通大学力学与航空航天学院，成都 611756；2.应用力学与结构安全四川省重点实验室，成都 611756）

引 言

铝合金作为工程中使用最广泛的轻金属材料之一，除了具有纯铝的一般属性之外，还因添加不同种类、不同含量的元素而具有其他独特的优良特性。因此，对于特定型号铝合金力学行为的研究具有重要意义。6005A 铝合金是一种典型的Al-Mg-Si系中等强度铝合金，它不仅具有密度低、比强度高的特性，还具有良好的尺寸稳定性和机械加工性，可以更好地实现主体结构的轻量化，因而在机械制造、交通运输和国防工业等领域得到广泛的应用[1-2]。在上述领域服役的过程中，材料难免会处于高应变率的工况，例如列车、汽车遇到高速撞击或军工设备加工时，材料会受到高应变率载荷作用。而在高应变率载荷下，材料可能会表现出与中、低应变率载荷下不同甚至截然相反的力学行为[3-6]。因此，揭示铝合金材料在不同应变率下的动态力学行为，对其在工程中的应用至关重要。

为了探究铝合金材料在不同应变率下的动态力学行为，学者们进行了大量的实验和本构模型研究。比如，Mylonas 等[7]研究了7449-T651 铝合金在103～104s-1应变率下的力学行为，发现其具有较强的应变率强化效应，并拟合得到了Johnson-Cook（JC）模型参数。Acharya 等[8]研究发现6061 铝合金在应变率高于3000 s-1时具有显著的应变率强化效应，且当应变率超过5500 s-1时，应变率敏感性显著增强，应力-应变曲线与Zerilla-Amstrong（ZA）模型较吻合。Tan 等[9]研究了7050-T7451 铝合金在较宽应变率条件下的拉伸力学行为，并根据材料的应变率效应，提出了改进的JC 模型。但针对6005A 铝合金高应变率下动态力学行为的研究相对不足，多集中在中、低应变率范围内。彭一波等[10]研究了6005A-T6铝合金在1～100 s-1中应变率的力学行为，提出了考虑动态回复的本构模型。孙巍等[11]研究了6005A-T6铝合金在1～200 s-1中应变率下的动态力学行为和微观形变机理，并标定了JC模型参数。

随着计算机科技的发展，有限元数值模拟技术在材料的动态力学研究中起到越来越重要的作用。但若要得到可靠的数值模拟结果，则既要保证建模的准确性，还要保证材料本构模型的准确性。Vilamosa 等[12]提出了适用于6082 铝合金在大应变、高应变率和高温下的物理型本构模型，并在有限元模拟中对其进行实现和验证。Zhang 等[13]对7075-T6 铝合金在10-3～103s-1宽应变率范围的力学行为进行了实验和数值模拟研究，提出了改进的JC本构模型，并验证其应用于宽应变率数值模拟的可靠性。Zhou 等[14]对Ti-6Al-4V 钛合金进行了霍普金森动态剪切和压缩实验，提出并验证了适用于钛合金超高速剪切的改进JC 模型。但这些模型并不能很好地适用于6005A铝合金的冲击数值模拟。

综上所述，针对6005A 铝合金在高应变率下的冲击动态本构模型和相关数值模拟研究尚未见报道。基于此，本研究针对在交通运输领域广泛使用的6005A铝合金进行准静态压缩实验和冲击动态压缩实验，研究该材料的应变率效应和热软化效应。基于实验研究，提出一种适用于6005A 铝合金的改进的JC本构模型。通过编写VUMAT子程序实现模型在ABAQUS 有限元软件中的应用，对6005A 铝合金动态压缩过程进行数值模拟，验证模型的合理性。

1 实验研究

实验采用高铁用6005A 铝合金作为研究对象。用RPL-100 材料试验机对6005A 铝合金试样进行准静态压缩实验。实验用圆柱形试样的尺寸为ϕ8 mm×6 mm。实验温度为室温，一共包括3种应变率，分别是0.0002、0.001、0.005 s-1。得到6005A 铝合金准静态压缩实验的真实应力-应变曲线如图1所示。

图1 准静态压缩真实应力-应变曲线

从图1 中准静态压缩真实应力-应变曲线可以看出，材料屈服强度不随加载应变率（ε'）变化而变化，应力-应变曲线的变化趋势基本一致，据此认为材料在准静态加载下不具有应变率效应。

采用分离式霍普金森压杆设备（Split Hopkinson Pressure Bar，SHPB），对6005A 铝合金材料进行冲击动态压缩实验。分离式霍普金森压杆已成为材料冲击动态力学性能测试中最常用的设备[15-16]，该装置示意图如图2所示。

图2 分离式霍普金森压杆装置示意图

动态压缩实验中子弹、入射杆、透射杆均采用18Ni 马氏体不锈钢材料，弹性模量为190 GPa。子弹尺寸为ϕ12.2 mm×200 mm，入射杆、透射杆尺寸为ϕ12.2 mm×1200 mm。试样尺寸与准静态实验一致，实验采用的应变率为500、1050、1600、2100 s-1。实验采集到的典型波形图如图3所示。

分离式霍普金森压杆实验技术的建立必须满足一维应力波假设，应力波在入射杆与透射杆中的传播不考虑弥散现象，该假设将试样两端的质点速度与实测应力波关联起来。测试局部原理图如图4所示，图中v1、v2分别为试样两端面速度，ls为试样的初始长度，εI、εR、εT分别为入射波应变、反射波应变、透射波应变。

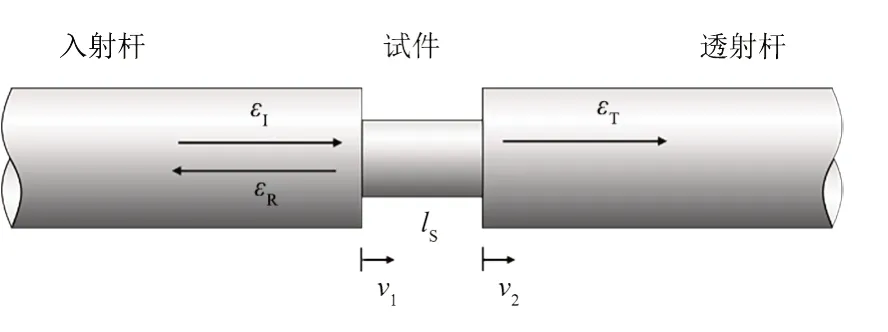
图4 霍普金森压杆测试局部原理图

利用“二波法”对采集到的动态信号进行处理，通过该方法即可计算出材料在冲击加载过程中的应变率ε'、应变ε和真实应力σ[17]，如式(1)～(3)所示：

式中，C0为杆中的波速，Ab、As分别为杆与试样的横截面积，Eb为杆的弹性模量。由于霍普金森杆冲击测试方法无法准确地表征韧性材料的弹性行为[18]，本研究仅针对冲击载荷下的塑性流动阶段进行分析讨论。室温下的冲击动态压缩真实应力-塑性应变曲线如图5所示。

由图5 可见，在动态加载下，6005A 铝合金具有较强的应变率强化效应，忽略实验曲线的震荡，不同应变率加载下的屈服强度在255～280 MPa 之间，且随着应变率的增加，呈现出软化趋势。

2 动态本构模型研究

为了描述和预测金属及其合金材料的冲击动态力学行为，在已有的研究中，研究者构建了多种本构模型，一般可分为经验型本构模型和物理型本构模型。典型的经验型本构模型有：JC 模型[19]、Khan-Huang（KH）模型[20]等。JC 模型包含了应变硬化项、应变率强化项和温度软化项，因其具有较高的适用性而被广泛应用。物理型本构模型主要有：ZA 模型[21]、Mechanical Threshold Stress（MTS）模型[22]等，其中，ZA模型包含两种不同的本构模型，用来描述不同晶体结构材料的冲击动态力学行为。

对比经验型和物理型两种本构模型，经验型本构模型主要基于实验研究结果而建立的，因其形式较为简洁直观且结果较为精确，能更好地服务于工程及数值仿真应用，缺点是物理意义较为薄弱；而物理型本构模型是从变形的物理机制角度出发，参数能够反映材料的内部状态，但往往形式复杂，不利于工程实际应用。

为了便于工程实际应用，根据材料的动态特性，此处首先采用JC 模型进行本构描述。由于本实验均在室温下进行，参考应变率取0.0002 s-1，模型可简化为：

式中，εp为塑性应变，ε'*=ε'/ε0'为无量纲应变率，ε'为实际应变率，ε0'为参考应变率，A、B、n、C均为拟合参数。

参阅文献[19]中的处理方法，取应变率为0.0002 s-1的准静态应力-应变曲线，通过曲线拟合可获得参数A、B和n的值。取准静态和不同应变率下2%塑性应变对应的流变应力，式(4)简化为σ=269.98(1 +Clnε'*)，通过拟合σ-lnε'*曲线，可获得参数C的值。拟合获得各参数见表1。

表1 JC模型参数

图6 所示为应变率效应的线性拟合曲线，可见其与实验结果并不吻合。在JC 模型中，材料的流动应力被视为与无量纲对数应变率呈线性关系。而由图6 中的实验结果可见，当应变率超过103s-1时，材料的应变率敏感性骤升，高应变率下流变应力与无量纲对数应变率不符合线性关系，因此，需要对JC模型进行适当的改进。

图6 应变率效应的线性拟合曲线

根据冲击动态压缩实验数据的分布特征，对JC模型的应变率项进行修正。Cowper-Symond 模型[23]认为流变应力与应变率呈幂指数关系，因此将JC 模型的应变率项改进为幂指数形式，如式(5)所示：

式中，σy为屈服应力，D和q为应变率相关的拟合参数。

幂指数形式的应变率项可以较好地描述6005A铝合金在高应变率下的应变率效应，如图7所示。

图7 改进后应变率效应的幂指数形式拟合曲线

进一步分析图5 可知，6005A 铝合金应变硬化率随应变率增加而逐渐降低。在冲击加载过程中材料变形产生的塑性功转化成热量，考虑到冲击加载是一个瞬态过程，这部分热量没有足够时间向外部耗散，由此产生了绝热温升现象，导致材料发生热软化。Kapoor等[24]的研究给出了金属材料塑性变形功转化为温升的计算公式：

式中，η为功热转化系数，ρ为材料密度，CV为材料定容比热容，ΔT为绝热温升。

将6005A 铝 合 金 的 材 料 参 数η=0.9，ρ=2700 kg/m3，CV=880 J/(kg·K)代入式(6)，得到了不同应变率下6005A铝合金的绝热温升与应变率之间的关系，如图8所示。

图8 绝热温升与应变率的关系

改进的JC模型（MJC）如式(7)～(9)所示。

式中，T*= ΔT/(Tm-T0)为无量纲温度，ΔT为绝热温升，T0为室温，Tm为融化温度，m为温度参数。

取准静态和不同应变率下2%塑性应变对应的流变应力，通过拟合应力-应变率曲线，可获得参数D和q的值。根据动态应力-应变曲线拟合可得m的值。改进的JC模型参数见表2。

表2 改进的JC模型参数

改进的JC 模型计算结果和实验结果的对比如图9 所示。从图9 可以看出，本构模型曲线和实验拟合曲线的吻合效果良好。显然，改进的JC 模型很好地描述了6005A 铝合金在高应变率下的力学行为。

图9 实验结果和改进的JC模型计算结果对比

3 有限元实现

3.1 算法推导及有限元实现

VUMAT 子程序的编写必须依据弹塑性力学理论，定义材料力学分析过程中的弹性阶段以及屈服过后的塑性阶段。应力的更新算法是编写VUMAT过程中的核心问题。基于改进的JC 模型和金属材料弹塑性演化法则，参照弹性预测-径向返回算法[25]进行算法编写。

依据弹性预测算法，假定材料单元初始处于完全弹性阶段，因此可以定义为试验弹性状态，得到当前增量步的弹性试验应力为：

随着应力的不断增大，材料最终会进入塑性阶段。这里采用Mises 屈服准则来判断材料是否进入塑性阶段，Mises屈服准则如下式所示：

式中，σeq为Mises 等效应力，Str为试验应力的偏量部分，εˉplt为等效塑性应变，T*t+Δt为无量纲温度，ft+Δt为屈服函数。

若f＜0，表示材料仍未到达材料的屈服极限，此时材料仍处于弹性变形阶段，当前增量步结束，应力更新为试验应力，即σt+Δt=σtrt+Δt；若f＞0，说明材料的应力已经超过Mises 屈服应力，进入塑性变形阶段，此时材料已不再符合完全弹性假设，需要对试验应力进行塑性修正。

根据塑性流动法则，可以得到等效塑性应变增量为：

式中，H是由式(7)求导得到的本构方程曲线的斜率，即塑性硬化模量，Δεpl为塑性应变增量。

最后由应力补偿原理可以得到当前增量步更新后的应力为：

式中为屈服面的法向。

给定材料的比热容、功热转化系数，通过式(9)来更新材料的温升。完成弹性和塑性过程后，更新耗散能等内变量。该算法适用于三维应力状态和平面应力状态，且可以很方便地将自定义的材料本构模型进行数值实现，因此得到广泛应用。

3.2 有限元建模验证及模拟结果分析

在ABAQUS 有限元软件中，使用上文基于弹性预测径向返回算法实现的VUMAT 子程序对4 个应变率下的动态压缩实验进行数值模拟，模型参数见表2。有限元模型由入射杆、试件和透射杆3部分组成，为了保证模拟的可靠性，建模尺寸与实际设备和试件尺寸一致，入射杆和透射杆均为ϕ12.2 mm×1200 mm，试件尺寸为ϕ8 mm×6 mm。由于模型整体形状规则，且变形量不大，因此单元类型采用八节点六面体线性减缩积分单元（C3D8R），能够在保证精度的同时节省算力。网格采用结构化划分方式，为保证计算精度，杆件网格尺寸为1，单元数量为168 000，节点数量为193 361，试件网格尺寸为0.4，数量为8256，节点数量为9295。接触模式采用入射杆、透射杆和试件之间的面-面接触，忽略试件与杆之间的摩擦。根据SHPB 设备的工作原理，模型整体不施加约束。有限元模型如图10所示。

图10 有限元模型示意图

模拟实验过程为入射杆端面施加压强载荷，直接输入实验提取到的入射应力波，入射应力波波形如图11所示。

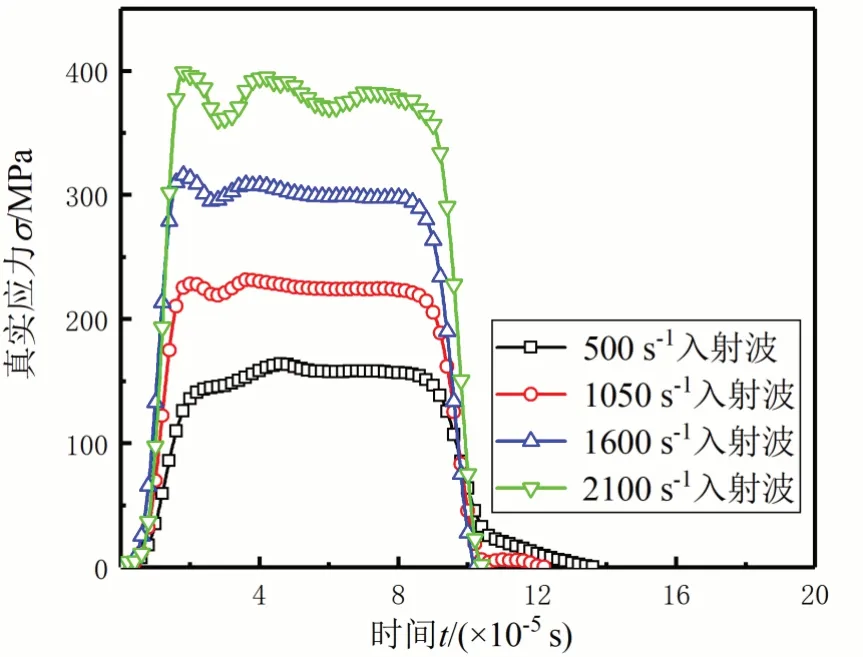
图11 入射应力波波形图

将入射波施加到入射杆端面进行有限元计算，并对计算结果进行分析。图12 所示为1050 s-1应变率下的实验与数值模拟变形结果对比图，由图可知材料并未出现损伤，假设材料为各向同性，模拟结果试件为轴向均匀压缩变形，其与实验结果相符。

图12 实验变形结果（上）和模拟变形结果（下）对比

将不同单轴加载条件下的实验应力-应变曲线与数值模拟应力-应变曲线进行比较，显示出良好的一致性，如图13所示。

图13 不同应变率下数值模拟结果和实验结果对比

通过图13中计算结果与实验结果的对比，验证了本文提出的本构模型及其数值算法的合理性和适用性。因此，该本构模型具有很好的预测能力。

4 结 论

本文对6005A铝合金进行了准静态和冲击动态压缩实验研究。根据实验结果，提出了改进的JC 模型用来描述6005A铝合金在高应变率下的冲击动态力学行为，并将改进的JC 模型应用到动态压缩数值模拟。结论如下：

1）6005 A 铝合金在准静态载荷下不具有应变率效应，且存在明显的应变硬化行为。冲击载荷下具有明显的应变率强化效应，并出现绝热温升现象。

2）改进的JC 模型可以很好地描述6005A 铝合金的冲击动态力学行为。

3）将改进的JC模型编写为VUMAT子程序用于冲击动态数值模拟，验证了改进的JC 模型对6005A铝合金动态压缩数值模拟的合理性。