精选数学好问题,驱动数学学习力——以最值问题习题课为例

玉云化

⦿ 武汉大学附属外语学校

八年级数学中的最值问题对于很多同学而言很难,不容易理解和掌握,考查的数学知识涉及轴对称、二次根式、勾股定理、平行四边形、一次函数等内容,知识点多,综合性强,这就需要教师精选具有趣味性、针对性、探究性的最值问题的解法,帮助学生对最值问题进行提炼、提升、探究,并进一步归纳总结,从而真正理解和掌握最值问题.通过教学过程激发学生学习兴趣,驱动学生追求知识本质,解决问题,进而培养学生思考探究、推理计算、归纳总结的学习能力.

本文中以人教版八年级下册“最值问题习题课”为教学案例进行分析,探讨课堂上如何精选数学好问题,驱动学生数学学习力,让每一个学生都融入到学习活动之中,使学生真正经历有意义的学习过程,取得好的教学效果.

1 教学设计

1.1 情境创设,提炼问题,激发兴趣

问题1如图1,教室的墙面ADEF与地面ABCD垂直,点P在墙面上.若PA=AB=5,点P到AD的距离是3,有一只蚂蚁要从点P爬到点B,它的最短行程是______.

图1

图2

设计意图：最值问题的引入不应局限于教材上的将军饮马问题,教师可以恰当地选编题目,巧妙运用生活中的趣味性问题引出最短路径这个重要知识,激发学生学习兴趣,有利于学生解题思维的汇聚与深入,为本节课开了个好头[1].

1.2 展开活动,提升问题,驱动学习

问题2如图3,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6.P为对角线BD上一点,则PM-PN的最大值为______.

图3

解析：本题主要考查了正方形的性质以及距离最值问题.凡是涉及距离的最值问题,一般要考虑关于线段的性质,结合轴对称变换来解决.以BD为对称轴作N的对称点N′,连接PN′,MN′,根据PM-PN=PM-PN′≤MN′,可得当P,M,N′三点共线(如图4)时,取“=”.此时,过点O作OE⊥BC于点E,即可得出MN′∥OE∥AB∥CD,∠CMN′=90°,则△N′CM为等腰直角三角形,即CM=MN′=2,于是PM-PN的最大值为2.

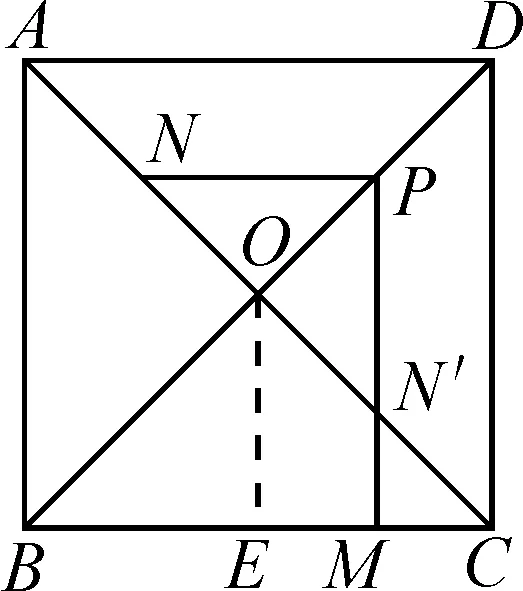
图4

设计意图：在引入问题1后,学生对最值问题产生了一定的学习兴趣与热情,此时顺势展开问题2的教学活动,提升问题难度,驱动学生攻克较难的最值问题,使得从提炼问题到提升问题的教学过程紧凑又条理清晰,有利于学生对最值问题的深刻理解和掌握.

1.3 自主探究,深化问题,巩固知识

问题3如图5,在平面直角坐标系中,点A的坐标为(3,1),直线l与x轴,y轴分别交于点B(-3,0),C(0,3),当x轴上的动点P到直线l的距离PE与到点A的距离PA之和最小时,则点E的坐标是______.

图5

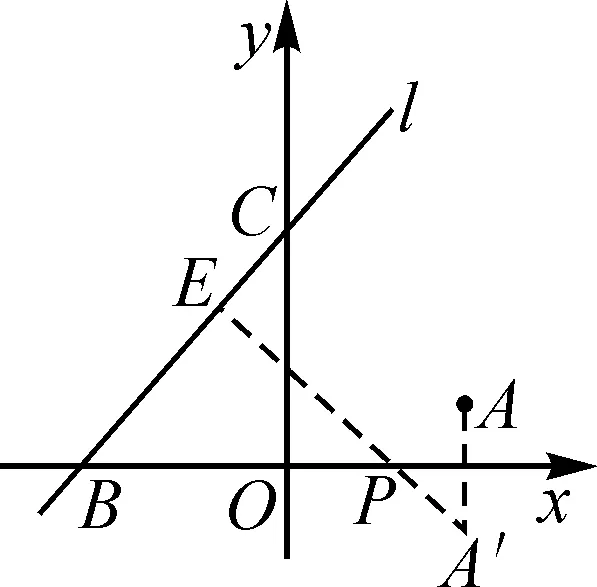
图6

设计意图：前两个问题由易到难,由浅入深,随着问题3的引入整个教学过程层层递进,深化学生对最值问题的认知,驱动学生利用求解经验,从一次函数背景下提炼出最值问题,有利于学生从解答过程中获得最值问题本质属性的自我解释,体现了数学知识的自然生长,教学过程流畅合理,又有显著的教学成效.

1.4 回顾反思,演练问题,归纳总结

练习1如图7,正方体的棱长为2,B为一条棱的中点.已知蚂蚁沿正方体的表面从点A出发,到达点B,则它运动的最短路程为( ).

图7

图8

练习3直线y=x+6与x轴、y轴分别交于点A和点B,x轴上有一点C(-4,0),P为该直线上一动点,当PC+PO值最小时点P的坐标为______.

设计意图：本环节的三个练习题既是前面问题的延伸,也是最值问题的深化,而且题目的设置关注了不同层次学生的发展,既满足全体学生对基础题型的掌握和巩固,也满足学有余力的学生的追求,驱动学生探究热情,让学生知道知识从“哪里来”往“哪里去”,有利于培养学生学习力.从真正意义上让学生解决问题,让课堂实现好的教学效果[2].

2 教学设计说明与思考

本节课通过“情境创设,提炼问题,激发兴趣;展开活动,提升问题,驱动学习;自主探究,深化问题,巩固知识;回顾反思,演练问题,归纳总结”四个环节,对最值问题进行整合,创造性、个性化地精选数学好问题,用这些好问题串联教学,生成灵活、丰富多彩的教学过程,让不同程度的学生都能得到不同的发展.

本节习题课从趣味性问题入手提炼最值问题,以学生身边的数学问题作为知识学习的切入点,突出数学与实际生活的联系,让学生知道知识从“哪里来”,即知识的源头,对学习知识产生亲切感,进而驱动学生愉快地投入到学习活动中;进一步展开学习活动,提升最值问题的难度,准确抓住知识的生长点,利用有层次的问题来驱动与激活课程的内在活力,让学生知道知识往“哪里去”,即在学科内不同章节知识间的综合应用;接着自主探究环节,准确抓住知识的延伸点,把握知识背后的数学本质与数学思想,深化最值问题,驱动学生的情感、思维、态度与价值观得到更加饱满的激活与释放,让学生真正经历有意思的学习过程,感悟学习数学的意义与价值.最值问题涉及的知识点多而复杂,想要在一节课中掌握最值问题并不是一件容易的事,学生难以消化.设计回顾反思这一环节的练习题,与例题一一对应,将最值问题串联于一体,实现知识的整合,通过归纳总结驱动学生巩固最值问题,确保本节习题课教学更加高效.

总之,这节习题课,精挑细选具有趣味性、针对性、拓展性、综合性很强的问题,这样驱动式的教学设计,驱动学生积极学习、深度学习与反思学习,进而理解、巩固、掌握知识,达到培养学生学习力的目的.