基于数学软件应用的高等数学教学改革研究

[摘 要]高等数学是高等院校理工科一门重要的基础理论教程,具有知识点多,难度大,理论抽象等特点,导致学生的学习和教师的教学压力都较大。在教学中引入如GeoGebra、Matlab等数学软件不仅能将高等数学中的概念形象直观地呈现给学生,而且可以锻炼学生运用抽象知识编程解决实际问题的能力。文章介绍基于GeoGebra和Matlab软件辅助教学的一些案例,涵盖了积分定义、Fourier级数、微分方程求解等问题。通过软件的信息化和动态可视化,激发学生的学习兴趣并提升其数学思维能力。
[关键词]高等数学;GeoGebra软件;Matlab软件;教学改革
[中图分类号] G642 [文献标志码] A [文章编号] 1008-2549(2023) 11-0090-04
高等数学是高等院校理工科一门重要的基础理论课程,其内容丰富,理论严谨,应用广泛,影响深远。李克强总理在2018年1月3日的国务院常务会议上指出:“数学是我国科学研究的重要基础。无论是人工智能还是量子通信等,都需要数学等基础学科作有力支撑。我们之所以缺乏重大原创性科研成果,卡脖子就是卡在基础学科上。”[1]然而,由于高等数学课程具有知识点多、难度大、理论抽象等特点,导致学生的学习和教师的教学压力都较大。例如,学生在初高中的数学学习中,所面对的往往是离散的、有限的、线性的问题。而高等数学课程中所处理的往往是连续的、无限的、非线性的问题。这就需要学生的思维认知有从有限到无限、从离散到连续的转换。此外,高等数学中的分类与整合、划归与转换、函数与方程等数学思维也是学生学习的一大障碍。以上原因导致很多学生在学习的过程中产生了畏难的情绪,对高等数学这门课程毫无兴趣。然而,作为其他专业课的基础,高等数学的重要性不言而喻。学生若无法理解高等数学的思维,即使在考试中侥幸过关,在后续其他专业课程的学习中依然会暴露出根基不牢固的缺陷。因此,如何提高学生的学习兴趣和加强数学思维能力一直是当今高等数学教学改革的重要课题。近年来,许多学者也对其进行了行之有效的探讨。[2-4]
近年来,随着计算机技术的发展,涌现出一大批优秀的数学软件,例如Matlab、GeoGebra、Mathematica、Maple等。这些软件在解决许多实际的数学问题中发挥着重要的作用。同时,利用这些软件的信息化和可视化功能对高等数学教学进行辅助,可以极大地引发学生的学习兴趣以及培养学生的数学思维。此外,这些软件强大的编程和计算功能也能帮助学生解决更多实际的数学问题。
本文将基于GeoGebra和Matlab这两款数学软件,对高等数学的信息化和可视化教学进行探究。对比这两款软件,其侧重点各有不同。GeoGebra作为一款优秀的动态几何软件,它最大的特点在于可以动态地演示高等数学中的许多定义,例如极限、定积分、级数等。从而在学生的脑海中刻画这些定义,加强对这些概念的理解和推广。Matlab作为一款专业的工程数学软件,其强大的计算功能可以帮助学生摆脱复杂的计算。同时,其强大的编程功能可以帮助学生利用抽象的知识去解决复杂的数学问题。
一、数学软件简介
本节将简单介绍GeoGebra和Matlab这两款数学软件。此外,由于两款软件的侧重点不同,我们还将其进行简单的对比,以得出在不同场景下两者如何取舍。
(一)GeoGebra软件简介
GeoGebra是一套包含处理几何、代数、微积分等功能的动态数学软件。它是由奥地利数学家Markus Hohenwarter以及其开发团队,为了让全世界的校园都可免费使用动态数学软件而共同开发的。GeoGebra的软件名是由“Geo”+“Gebra”组成,其意思为几何(Geometry)与代数(Algebra)。该软件具有开源、体积小、动态可视化等优点,并且相较于其他数学软件,GeoGebra的操作比较容易上手。因此,GeoGebra在中小学和大学的数学教学中得到了广泛的应用。[5-7]
GeoGebra的软件界面分为代数区和绘图区,其代数功能和动态几何作图功能可以帮助学生对高等数学中的各种对象(点、线、面、方程)有直观理解。此外,在绘图区任意空白处点击可以构建一个数值的滑动条,通过拖动滑动条可以使得研究对象产生直观的动态变化。借助此软件,我们可以设计极限、定积分等定义里面一系列动态过程,例如,数列动态逼近、定积分的细分求和、图形的相交旋转等。以上种种优点,有利于加强学生对于概念的理解以及激发学生的学习研究兴趣。此外,作图生成的“ggb”文件非常小巧(几十Kb至一百Kb),可以嵌入PPT中。该软件也有丰富的教学资源,教师可以方便地加以利用。
(二)Matlab软件简介
Matlab软件是美国MathWorks公司出品的商业数学软件,其名称是由“Matrix”“Laboratory”两个单词组合而成,意为矩阵实验室。作为一款专业的工程类数学软件,它将矩阵计算、数值分析、非线性动态系统的建模与仿真和科学数据可视化等一系列强大的功能集成在一个视窗环境中,为科研、工程设计等众多科学领域提供了强大的帮助。Matlab的强大功能在此我们不进行过多赘述,读者可以参考专业书籍。[8]
在高等数学的教学中,我们可以将Matlab有效合理地融入其中。[9-11]一方面,這可以帮助学生省去一些烦琐的计算,另一方面,其引导了学生学习一款实用软件、练习了编程技巧和提高了利用高数知识解决实际问题的能力。
(三)两款软件对比
两款软件各有优点,并无孰优孰劣之分,我们需要在不同的场景下合理地选择不同的软件。例如,在高等数学的许多概念教学中,可以借助GeoGebra对定义进行动态化、直观化的表述。而当涉及一些复杂的计算,例如微分方程的求解等,Matlab强大的计算以及仿真模拟功能可以帮助我们快速得出结果并对其进行分析。
二、GeoGebra在高等数学教学中的具体应用
(一)GeoGebra融入定积分的教学过程
定积分是学生正式进入积分学的学习,而要使得学生了解定积分的本质,几何直观图形的展示是必不可少的。在此,教师可以利用GeoGebra软件来生动讲述有关内容。这不仅能让同学们感悟到积分学的魅力,而且能了解到GeoGebra功能的强大。
案例1:定积分定义的几何动态展示
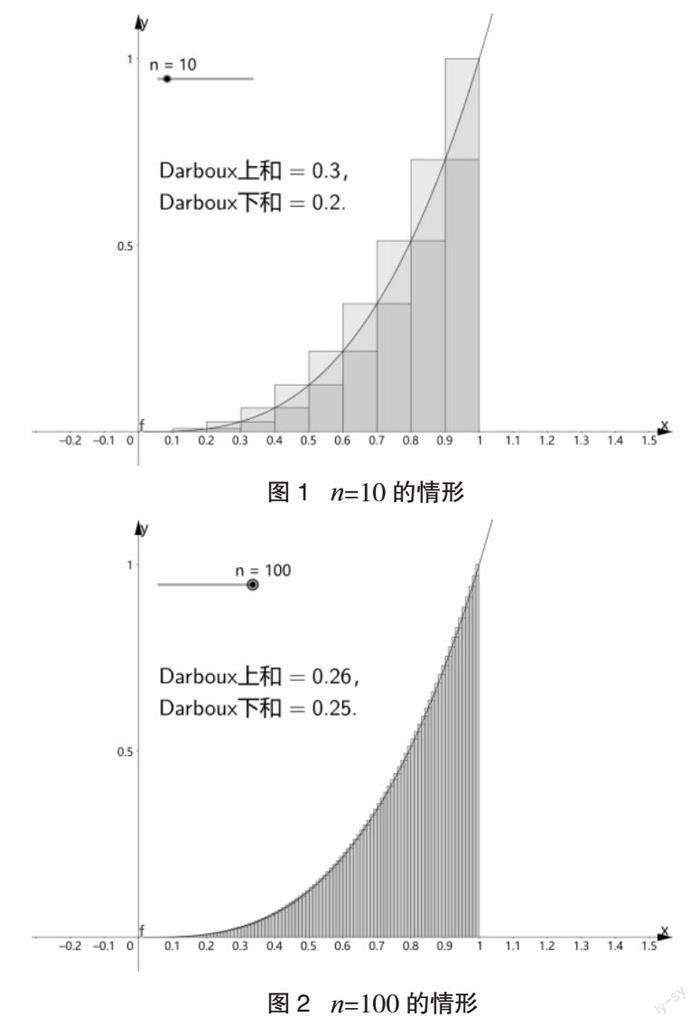
我们以∫01x3dx这一积分为例子。首先,在GeoGebra软件中输入函数f(x)x3,并把[0,1]區间等分成n份,其中n设置成滑动条。分别计算其即上积分与即下积分。观察到随着n的增大,两者都会越来越逼近曲边三角形的面积,图1和图2分别表示在分割n=10和n=100情形下,上积分、下积分与曲边三角形面积的关系。
借助这个例子,学生可以很直观地理解定积分思想,即分割、求和、取极限,从而理解定积分的定义。
(二)GeoGebra融入Fourier级数的教学过程
作为高等数学的重点和难点之一,Fourier级数在光学、电学、声学等都有极为广泛的应用。利用GeoGebra来刻画动态的逼近过程,一方面能让学生认识到Fourier级数的主要思想,另一方面也能让学生体会到数学之美。
案例2: 函数展开成Fourier级数。
我们以分段函数
为例:首先在GeoGebra软件中输入该函数,设置滑动条n,在代数区输入变量A=序列(f(x)((cos(nx)/(π)),-π,π),n,0,N)以及B=序列(f(x)((sin(nx)/(π)),-π,π),n,1,N)。最后,根据Fourier级数的展开表达式,我们可以输入系数AO=((元素(A,1)/(2)),AX=序列((元素(A,n+1)cos(nx),n,1,N)以及BX=序列((元素(B,n)sin(nx),n,1,N),则F(x)=AO+总和(AX)+总和(BX)。通过移动滑动条,学生可以观察到取Fourier级数的有限项逼近到函数的动态过程,见图3和4。学生容易发现,该级数的前n项和随着n的增大,越来越接近给定的函数f (x)。并且在f (x)的间断点处,级数的和为 ,此即为Dirichlet定理的结论。
三、Matlab在高等数学教学中的具体应用
常微分方程是高等数学中最体现微积分价值的一部分。诸多的实际问题都可以利用数学建模来转化成常微分方程求解,并解释实际问题所体现的客观现象。常微分方程在很多实际问题上是很难求出解析解的,因此如何利用好Matlab来求数值解显得更为重要。
案例3:(导弹追击问题)假设导弹A距离正在以最大速度行驶的船舰B 1km处,且船舰匀速向前行驶而导弹头始终指向船舰,一段时间过后,最终将其击落。不妨考虑船舰以2km/h的最大速度直线匀速行驶,而导弹速度始终为10km/h。求解船舰在相距导弹1km时需要多久才能击落船舰以及此时船舰能行驶多远。
解:建立直角坐标系,可以假定导弹A位于原点处,船舰B位于(1,0)处。设在T时刻导弹位于坐标中的点M(x(T),y(T))处,此时船舰B位于点N(1,2T)处。由条件容易得到微分方程: 。
结合初始条件并利用Matlab求解,其代码如下:
syms y(x);
g=1/5.*sqrt(1+diff(y,x,1).^2);
f=(1-x).*diff(y,x,2);
Dy = diff(y,x);
cond = [y(0)==0, Dy(0)==0];
ySol= dsolve(f==g, cond);
ySol = simplify(ySol)
ezplot(ySol(2),[-0.1,1.1])
title(' ');
hold on
plot([1,1],ylim,‘m—);
text(0.3,0.04,‘导弹轨迹;,‘FontSize,14);
text(0.78,0.02,‘船舰轨迹,‘FontSize,14);
由上述程序可求得方程的解为
其轨迹如图5所示。将x=1代入,利用Matlab计算出y的值,得出y(1)=0.2083。从而T=y(1)/2=0.1042h,这表明了在大约6分钟后击落,而此刻船舰行驶了208.3m。
四、结语
本文介绍了GeoGebra和Matlab这两款数学软件在高等数学教学改革中的应用。让学生对高等数学充满兴趣并且能扎实掌握并熟练运用高数知识一直是高等数学教学改革的重要目的之一。然而,在高等数学的传统课堂教学中,往往是教师利用黑板或者PPT灌输式地将理论、知识、证明技巧等传授给学生。借助GeoGebra和Matlab这两款数学软件,教师可以将高等数学中的很多概念通过数形结合的方法形象直观地呈现给学生,加强学生对概念的理解并激发学习兴趣。结合近年来的网络教学经验,这两款软件更适合线上线下混合使用模式。教师在线上对软件的使用做了具体的演示,学生在线下可以利用软件丰富的网络资源巩固和拓展所学到的知识。将数学软件引入高等数学教育的课堂后,也对教师提出了更高的要求。教师必须熟练地使用GeoGebra、Matlab、Mathematica等数学软件,并将其有机地融入教学中。只有这样,才能把传统的“教师主宰性”课堂转换为师生探究型课堂,从而提高教学质量以及推动高等数学课堂的现代化发展。
参考文献:
[1]李克强.为何反复强调数学等基础学科的重要性?[EB/OL].中国政府网,http://www.gov.cn/guowuyuan/2018-01/04/content_ 5253247.htm.
[2]杨宏林,丁占文,田立新.关于高等数学课程教学改革的几点思考[J].数学教育学报,2004(2):74-76.
[3]吴振英.新工科背景下高等数学课程教学改革探索[J].高教学刊,2022,8(21):144-147.
[4]余宏旺,胡锐,魏云峰.以生为本理念下高等数学研究导向型教学实践探索[J].教育教学论坛,2022(34):81-84.
[5]李建涛.高等数学课程中基于GeoGebra软件的信息化教学[J].辽宁大学学报:自然科学版,2021,48(4):381-386.
[6]牛海军.数学软件GeoGebra在高等数学教学中的应用[J].牡丹江教育学院学报,2016(1):63-64.
[7]张敬信.基于GeoGebra构建高等数学动态图形化教学资源库[J].科技风,2022(3):142-144.
[8]李晓东.MATLAB从入门到实战[M].北京:清华大学出版社, 2019.
[9]李娜,仁庆道尔吉.MATLAB在高等数学教学中的应用研究[J].大学教育,2012,1(11):66-67,74.
[10]黄慧青.MATLAB在高等数学教学中的应用[J].教育教学论坛,2019(19):96-98.
[11]张凤,郭洪杰,刘强. MATLAB在高等数学教学中的可视化应用[J].科技风,2022(15):109-112.
(责任编辑:刘洁)
Research on the Reform of Higher Mathematics Teaching Based on the Application of Mathematical Software
Cheng Kun
(School of Information Engineering, Jingdezhen Ceramic University)
Abstract: Higher mathematics is an essential foundational theoretical course in science and engineering disciplines at higher education institutions. It is characterized by a large number of concepts, high difficulty, and abstract theories, resulting in significant pressure on both students' learning and teachers' instruction. Introducing mathematical software such as GeoGebra and Matlab into teaching not only presents concepts in higher mathematics to students in a visually intuitive way but also helps them develop the ability to apply abstract knowledge to solve practical problems through programming. This article introduces some cases of teaching assistance using GeoGebra and Matlab, covering topics such as integral definition, Fourier series, and solving differential equations. Through the informatization and dynamic visualization provided by the software, students' interest in learning is stimulated, and their mathematical thinking abilities are enhanced.
Key words: Advanced Mathematics; GeoGebra Software; Matlab Software; Teaching Reform
基金項目:景德镇陶瓷大学博士科研启动基金项目:几类Kirchhoff方程解的存在性(000/20298612)。
作者简介:程琨(1990—),男,博士,讲师,研究方向:大学数学教学,偏微分方程等。

