基于波场分离的不规则地形下地震波输入方法

张佳文，李明超，韩 帅，闫文钰

(1.水利工程仿真与安全国家重点实验室，天津大学，天津 300350；2.香港理工大学建筑与房地产学系智能建造实验室，香港 999077)

不规则地形条件对地震波传播路径和地震烈度异常区的发生均有重大影响，主要体现在局部地形对地震波的散射和波型转换[1-3]，国内外震害资料也反映了其对地表位移和加速度幅值放大效应等的巨大影响[4-6]。因此，场地反应分析一直以来都是地震学及工程抗震领域关注的重点。此外，近年来大量台阵记录均证实了地震波入射角度的存在[7]，斜入射地震波对结构物振动响应的危害性成为共识[8-9]，地震波的入射角度与行波效应等问题的引入使得不规则地形场地地震波场的求解难度进一步升级。

目前，场地反应的求解主要有解析法和数值模拟法[10]，解析方法包括波函数展开法、分离变量法、几何射线理论等十几种类型[11-14]，已成功应用在了规则局部地形中，例如：均质长方形场地[15]、半圆和半椭圆形峡谷[16]、任意圆弧凹陷场地[17]等。然而解析方法限制条件较多，针对场地介质本构关系复杂或形状不规则地形条件，全域波场的解析求解难以实现。相比而言，数值模拟方法适用范围更加广泛，且能更好地应用到抗震分析中[18]，各类基于有限元法、有限差分法和边界元法等的研究也正在蓬勃发展[19-21]。斜入射地震波作用下不规则地形地震波场的求解作为一个较难的课题，可通过解析推导与数值模拟相结合来实现。

ASHFORD 和SITAR[22]基于广义一致透射边界等分析了陡坎地形在倾斜SH 波作用下位移等的放大效应，将不规则场地分区域进行求解，并首次引入了此类问题的时域化解法，但波场计算的精度不高且并未研究平面内的波场；李山有和廖振鹏[23]应用显式有限元法对波动方程进行离散化求解，研究了断层台阶场地的反应特点，并指出了地表运动的差异性，有效考虑了不规则地形对地震波型的转换问题，然而波场计算依赖于边界条件且计算繁琐；顾亮等[24]基于有限元数值模拟与透射边界理论，研究了SV 波斜入射下陡坎地形地表峰值加速度的响应问题，文中对自由波场的计算较为简便，但对局部地形的散射问题考虑不充分，因此精度不高；赵密等[25]基于黏性边界条件推导了边界上的等效节点力，研究了SV 波倾斜入射至阶梯型场地时的地震动输入方法，可将地表位移的峰值误差控制在5%以内，但并未详细介绍垂直入射与斜入射时地震波场计算的不同之处；BAO 等[26]提出了混合波场的思路，结合有限元法和波动输入方法研究了SV 波垂直和倾斜入射下阶梯型地形的地震动输入方法，其精确度和效率有了较大的提升，然而地形条件和波型较为单一。以上几类典型的方法不断提升了计算精度与适用范围，但是对局部地形的散射问题考虑还不够充分，所采用的地震波波型、地震入射角度、场地地形条件等也有限，且在地震动输入时普遍对人工边界的限制条件较高，计算过程十分复杂；因此，亟需提出更为通用和高效的地震波场计算与输入方法。

本文提出了一种不规则地形条件下的地震波输入方法。依据地震波传播规律进行波场分离，再将非外行波场转换为人工边界上的等效节点力形式以完成计算。该方法有效考虑了局部地形中散射波场的影响，计算过程明晰简便，易于推广至复杂场地条件。验证部分选用了不同的地形条件，将计算结果分别与精确解、参考解、成熟方法解进行对比；并应用到多组斜入射P 波和SV 波作用下场地的振动的分析中。

1 方法原理

1.1 地震波场分离

不规则地形条件下场地的全域自由波场无法统一求解，需要在各个边界上针对不同地形特征与输入条件分开计算。李山有和廖振鹏[23]提出地震波的输入应满足非外行波的条件(非外行波即通过边界向有限域内传播的波和平行边界的地震波)，并证明了地震波垂直入射情况下，底边界的非外行波即入射波，而侧边界的非外行波可看作与远场介质对应的自由波场。而本实验进一步考虑到倾斜入射的情况，认为斜入射情况下(以左下角入射为例)，右边界区域在初始阶段便存在反射波场，因此非外行波场也只有入射波场。此外，杜修力和赵密[27]曾也指出，目前所有的人工边界都只能模拟传递到无限域的外行波，而由结构物存在、不规则地形条件、局部地质等引发的散射问题，都需在边界处进行波场分离。

因此，根据地震波入射、反射和散射等原理，首先在不规则地形场地的各个边界面上进行波场分离。当地震波垂直入射时，在底面边界上将波场分为入射波场和边界外行场，左右边界面上分离为自由波场和散射场；当地震波倾斜入射时(以从左下角入射为例)，在底面边界和右面边界将波场分为入射波场和边界外行场，而左面界面上则分离为自由波场和散射场即可。进而输入非外行波场，如图1 所示：1) 垂直入射情况下在底部边界输入入射波场，两侧边界输入各自高度对应的自由波场；2) 倾斜入射情况下，在底部边界和右侧边界输入入射波场，在左边界输入自由波场。

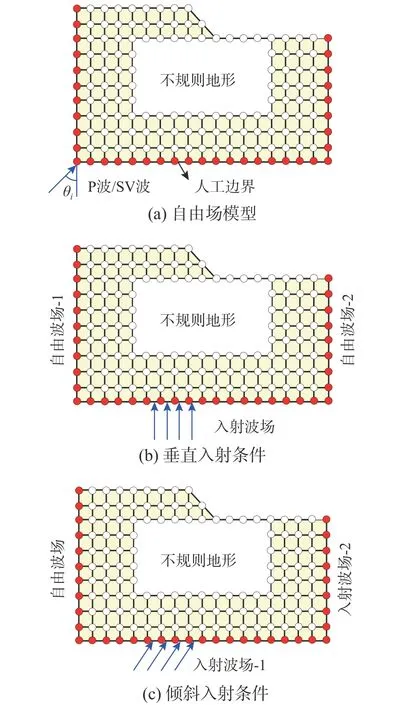
图1 不规则地形下各边界地震波场输入Fig.1 Input of seismic wave field at each boundary under irregular terrain

1.2 地震波场求解

入射波场和自由波场是决定场地响应的主要因素，需要分别确定；由局部地形引起的散射波场则通过有限元计算体现。

1) 入射波场：地震的入射波场求解可以直接通过几何推导实现。如图2 所示，利用人工边界截断形成一定的有限域空间，假设地震P 波从左下角(x0,y0)点进行入射且振动位移时程为uP(t)。由于P 波入射时质点振动方向与传播方向一致，其入射波场的水平和竖向位移计算公式如下：

图2 斜入射P 波作用下的地震波场Fig.2 Seismic wave field under obliquely incident P waves

式中：θ1为P 波入射的角度；Δt1即为P 波传播到边界上任一节点(x,y)的时间；cP为地震P 波的波速。

假设地震SV 波从左下角(x0,y0)点进行入射且振动位移时程为uSV(t)，由于SV 波入射时质点振动方向与传播方向相互垂直，其入射波场的水平和竖向位移计算如下：

式中：θ2为SV 波入射的角度；Δt2即为SV 波传播到边界上任一节点(x,y)的时间；cSV为地震SV 波的波速。

2) 自由波场：如图3 所示，自由波场包括入射场和反射场，例如P 波斜入射时又会在界面分层处同时产生反射P 波和反射SV 波，且幅值系数发生了变化，因此不能通过简单的几何推导求得。

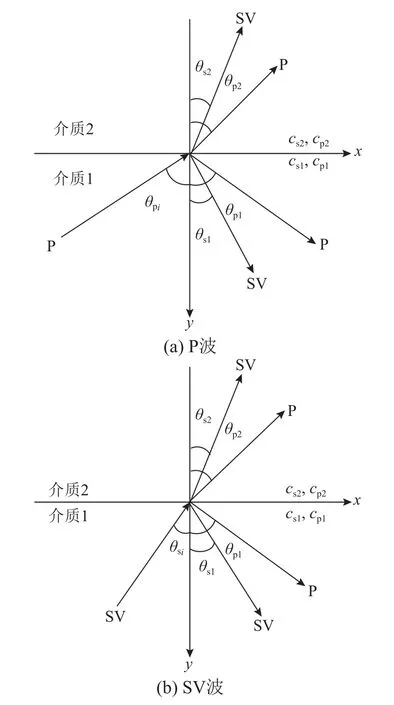
图3 斜入射地震波传播规律Fig.3 Propagation law of obliquely incident seismic waves

目前在研究斜入射地震波下场地的自由波场时，主要有频域和时域两种方法，后者更适用于复杂的场地条件且与现代大型计算软件匹配良好，因而广泛使用。目前比较流行的有一维时域化方法[28]，其结合了集中质量有限元法和中心差分法以建立二维波动方程，计算出单一垂线上节点的位移，再通过几何推导扩展到全域波场。

主要过程如下：图4 为离散化后的半空间模型，横向和竖向网格尺寸为Δx和Δy，地震P 波或SV 波从模型底部的人工边界进行输入。将y轴上的三类节点包括中间节点(0,n)、自由表面节点(0, 0)和人工边界上的节点(0,N)在PΔt时刻的运动方程表示如下：

式中：M、C、K分别为节点的质量、阻尼和刚度矩阵，下标为节点的坐标信息；CB和FB分别为边界的阻尼系数和需要输入的集中力。在P 波和SV 波入射时分别有不同的FB计算方法，求解上述方程组，即可确定半空间内y轴上所有节点在(p+1)Δt时刻的位移，再结合几何关系推广到全域即可计算出整个半无限空间的自由波场。

1.3 地震波动输入

地震属于振动中的外源问题，在进行波场推求后还需进行地震动输入才能准确计算场地的动力响应，人工边界和地震动输入方式的选择是计算中的两个关键环节[29]。数值模拟过程中通常在无限域地基中截取感兴趣的部分作为有限域，并在截断处赋予各类人工边界，其主要作用是吸收外行波以达到对无限地基辐射阻尼的模拟。地震动输入则主要分为振动法和波动法，波动法最早由刘晶波和吕彦东[30]于1998 年提出，可有效克服振动法中对于场地材料、激励方式和边界处理上的简化造成的误差，可以处理地震波斜入射问题和复杂场地的输入问题，也因其时空解耦性的特点而与各类大型通用软件适配性极高，是目前模拟精度最高且最为流行的地震动输入方法。波动法的核心原理是将地震动输入转换为人工边界上的等效荷载力，需要引入黏性边界和黏弹性边界等人工边界；因此需要同时计算由自由场产生的应力和引入边界后的附加应力，针对不同网格尺寸和方向不同的应力条件也需逐一判断，计算过程十分复杂；尤其是考虑复杂场地条件时，等效荷载力计算的难度显著增大，尤其是所要探讨的不规则地形条件，传统的波动方法已不具备高效处理的能力，亟需进行优化。

刘晶波等[31]和宝鑫等[19]对波动法进行了改进，从一维土柱模型入手证明了在边界节点附近的所有相邻节点同时施加入射波场位移或自由波场位移，再将输入位移后计算得到的荷载力反向输入回模型中可完成地震波输入，进而提出了基于人工边界子结构的地震波动输入方法，如图5所示。图5(a)为不规则地形的有限元模型；图5(b)中将含有边界节点的所有单元称为边界子结构，将地震波场位移时程输入到子结构中可得到边界节点的反力，经过证明此反力在数值上恰好等于需要的等效荷载力；图5(c)表示重新在边界节点上输回此反力即可实现波动输入。该方法保留了波动法的诸多优势并简化了等效荷载力的计算流程，避免了复杂等效节点力的过程，可成功地将不规则地形场地的地震波输入问题聚焦为地震波场求解问题。

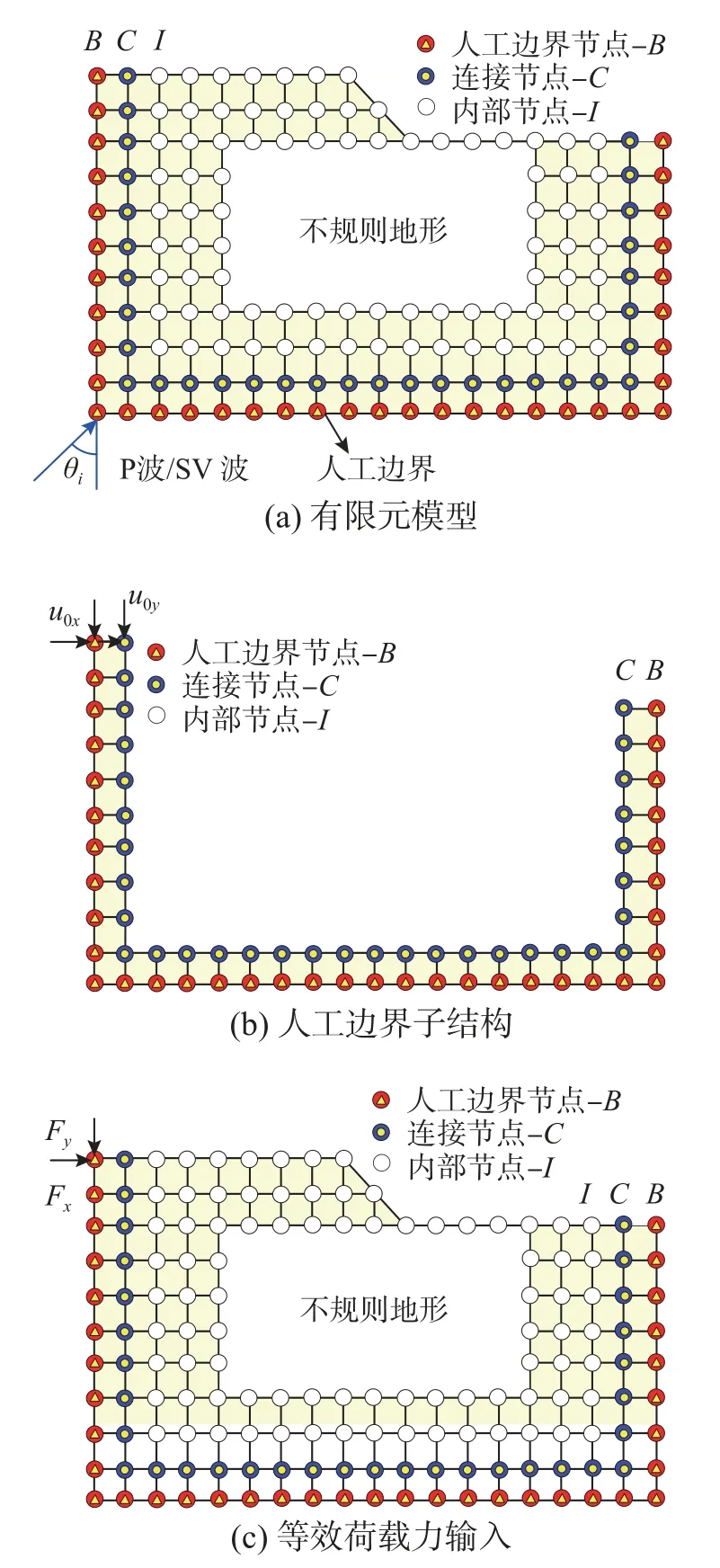
图5 基于人工边界子结构的波动输入方法Fig.5 Wave input method based on substructure of artificial boundaries

2 算例验证

2.1 有限元模型

为了验证所提出的方法在各类不规则地形条件下的适配性，分别以阶梯型、V 字河谷型和梯形河谷型这三类工程中常见的不规则地形条件为例进行验证。图6 展示了三类地形有限元模型尺寸信息，在模型的左侧、右侧和底面边界分别采用了黏弹性边界条件进行约束。由于斜入射地震波场在不规则地形条件下的频域解析解不能求得，可扩大截取的有限域场地范围，采用远置边界的方法保证地震波不会通过人工边界反射后再回到需要观测的部位，并将远置边界法得到的结果作为有限元近似精确解(简称参考解)。图7 展示了上述三类场地相对应的远置边界有限元模型信息，边界均无任何约束。图6 和图7 中的规则部分为正方体网格，尺寸为1 m×1 m，A点、B点、C点为自由表面观测点，利用观测点的位移信息来进行对比验证。三类场地的材料参数及地震波速信息见表1。

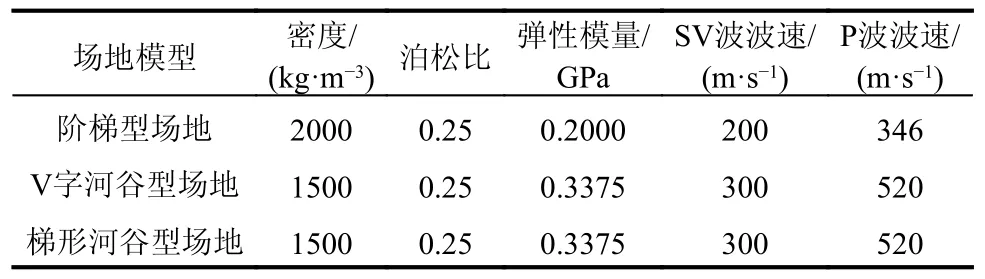
表1 场地模型参数Table 1 Model parameters of the site

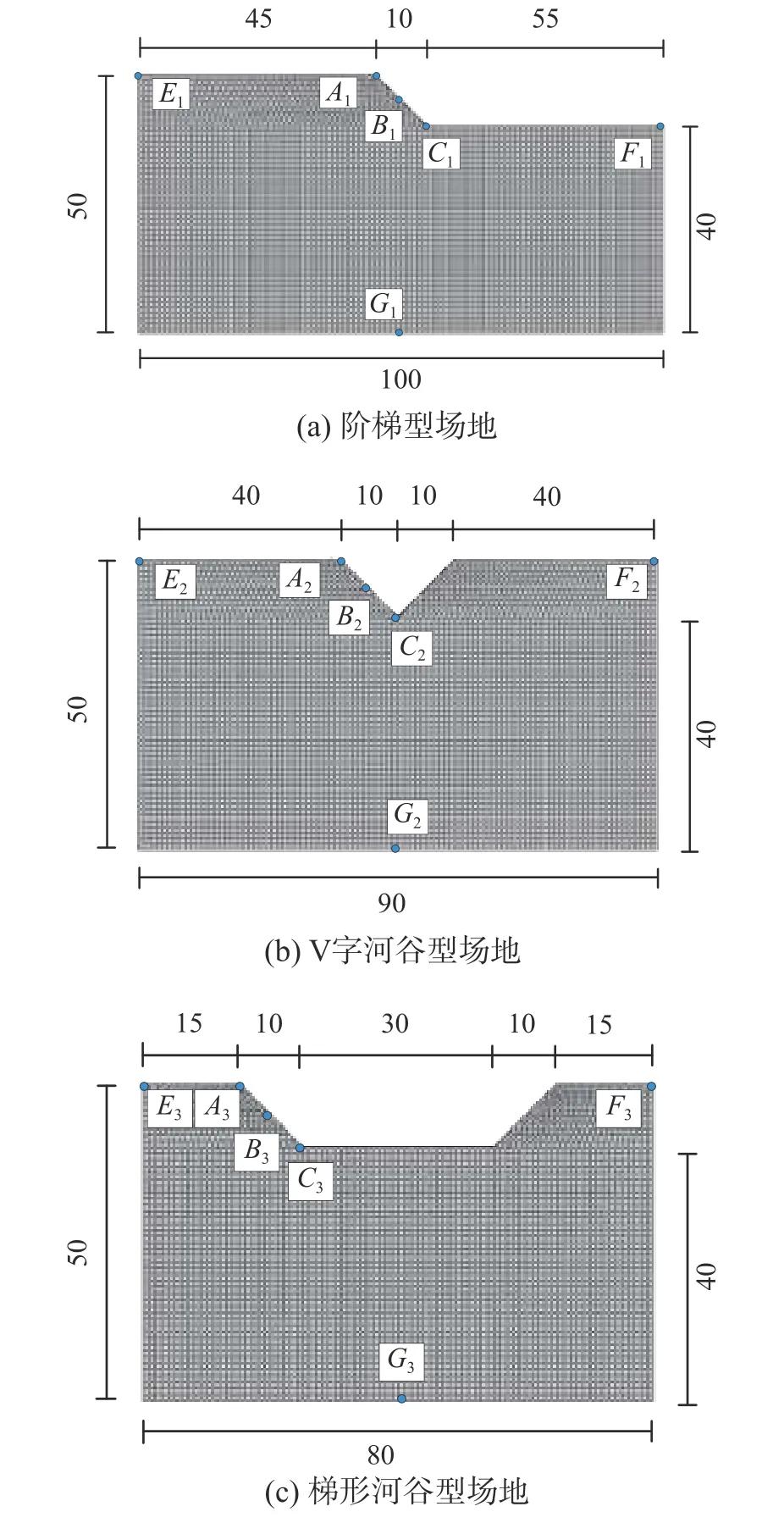
图6 不规则地形场地的有限元模型 /mFig.6 Finite element model of irregular terrain site

以平面P 波和SV 波为例，倾斜入射时假设地震波统一从场地的左下角进入，若考虑从右下角只需将左右边界的波场分离方式互换即可，此处不再详细展开。选用脉冲地震波的时程曲线及傅里叶谱曲线如图8 所示。两种场地模型参数条件下满足一维时域化方法自由场计算精度的时间间隔分别为0.0029 s 和0.0020 s，统一选取0.002 s 作为地震波的输入以及后续有限元计算的时间间隔。不规则地形条件下各个边界输入波场的计算方法参考第1 节；而在远置边界法中，各边界均采用对应高度的自由波场即可。

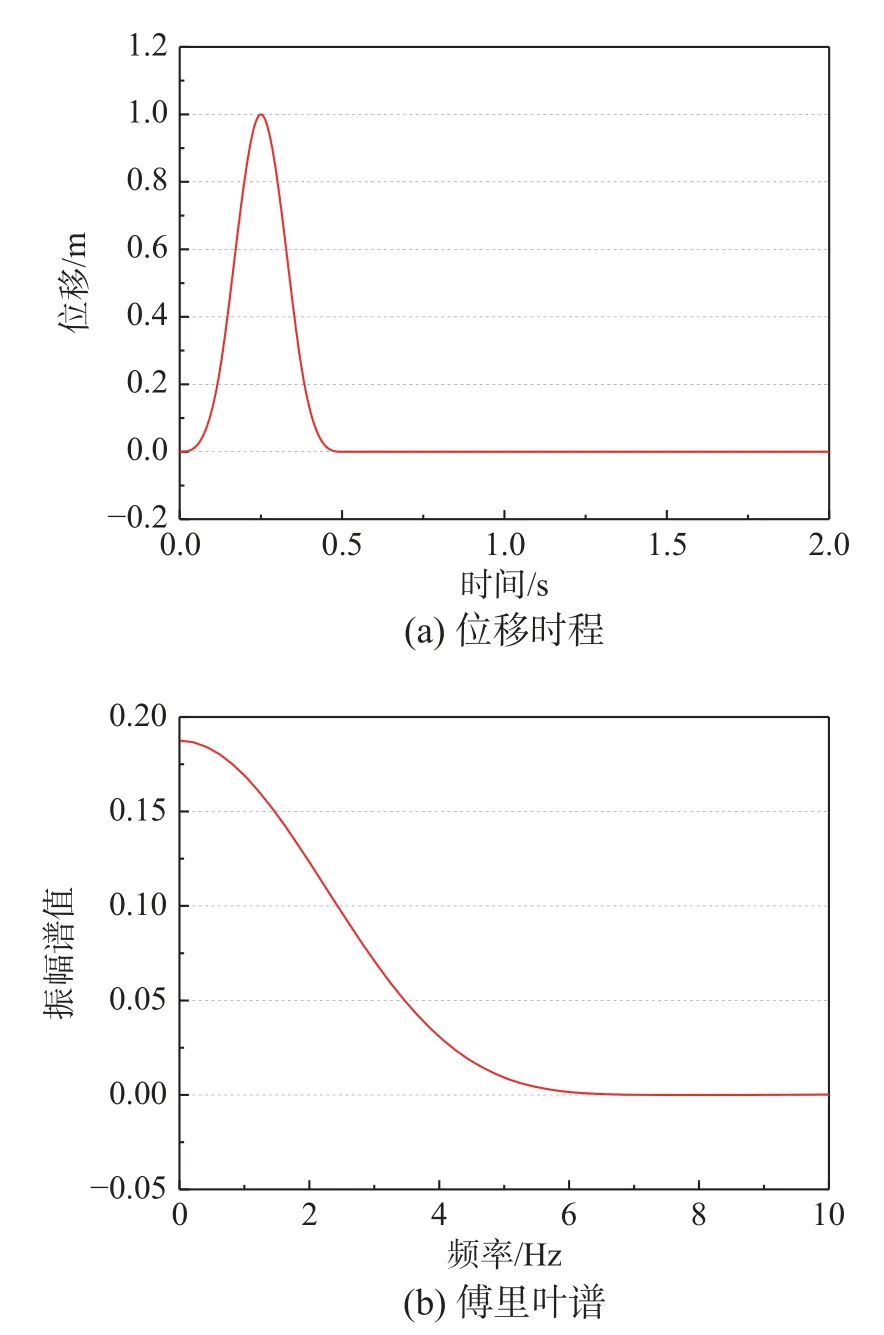
图8 入射脉冲波的位移时程和傅里叶谱Fig.8 Displacement and Fourier spectrum of the incident seismic wave

共进行了4 组验证实验，选取了入射角度为0°和30°的平面脉冲P 波和入射角度为0°和15°的平面脉冲SV 波。其中，P 波和SV 波垂直入射计算时选用阶梯型场地，P 波30°入射选用梯形河谷型场地，SV 波15°入射时选用V 字河谷型场地，可充分验证方法对不同条件下的适配性。波场计算过程均利用python 编程，有限元计算过程在大型通用软件ABAQUS 中进行。

2.2 P 波入射情况验证

如图9 所示，将节点等效荷载力输入到有限元模型的人工边界后，得到了P 波垂直和倾斜入射下不规则场地的自由表面点A、点B、点C的横向与纵向位移情况，图例中的Ux和Uy分别代表观测点横向和纵向位移，为将结果显示清楚模拟解部分的位移时间间隔扩大了15 倍。可以看出本文方法的结果(模拟解)与参考解吻合很好。其中，需要注意的是由于远置边界模型尺寸和原有的不规则地形尺寸不同，在比较位移结果时需要去除前面一段时间(地震波从远置边界到原有边界处的时间)。此外，观察结果发现：1) 观测点的竖向高度越高，其位移幅值越大；2) 虽然两个案例的场地参数不同，但由于输入的脉冲波位移一样，可以在位移幅值上做出比较，P 波倾斜入射相较于垂直入射时，横向位移幅值增大，竖向位移幅值略有减小。这两点与实际情况相符。

图9 P 波入射下自由表面点位移Fig.9 Displacement of free surface under incident P waves

2.3 SV 波入射情况验证

图10 为SV 波垂直和倾斜入射下自由表面点A、点B、点C的水平与竖向位移情况，结果同样与参考解几乎吻合，说明方法对P 波和SV 波都是通用的。结果发现：1) 观测点的竖向高度越高，其位移幅值越大，规律同P 波相同；2) SV 波倾斜入射相较于垂直入射时，横向位移幅值减小，竖向位移幅值增大。这两点也符合实际规律。

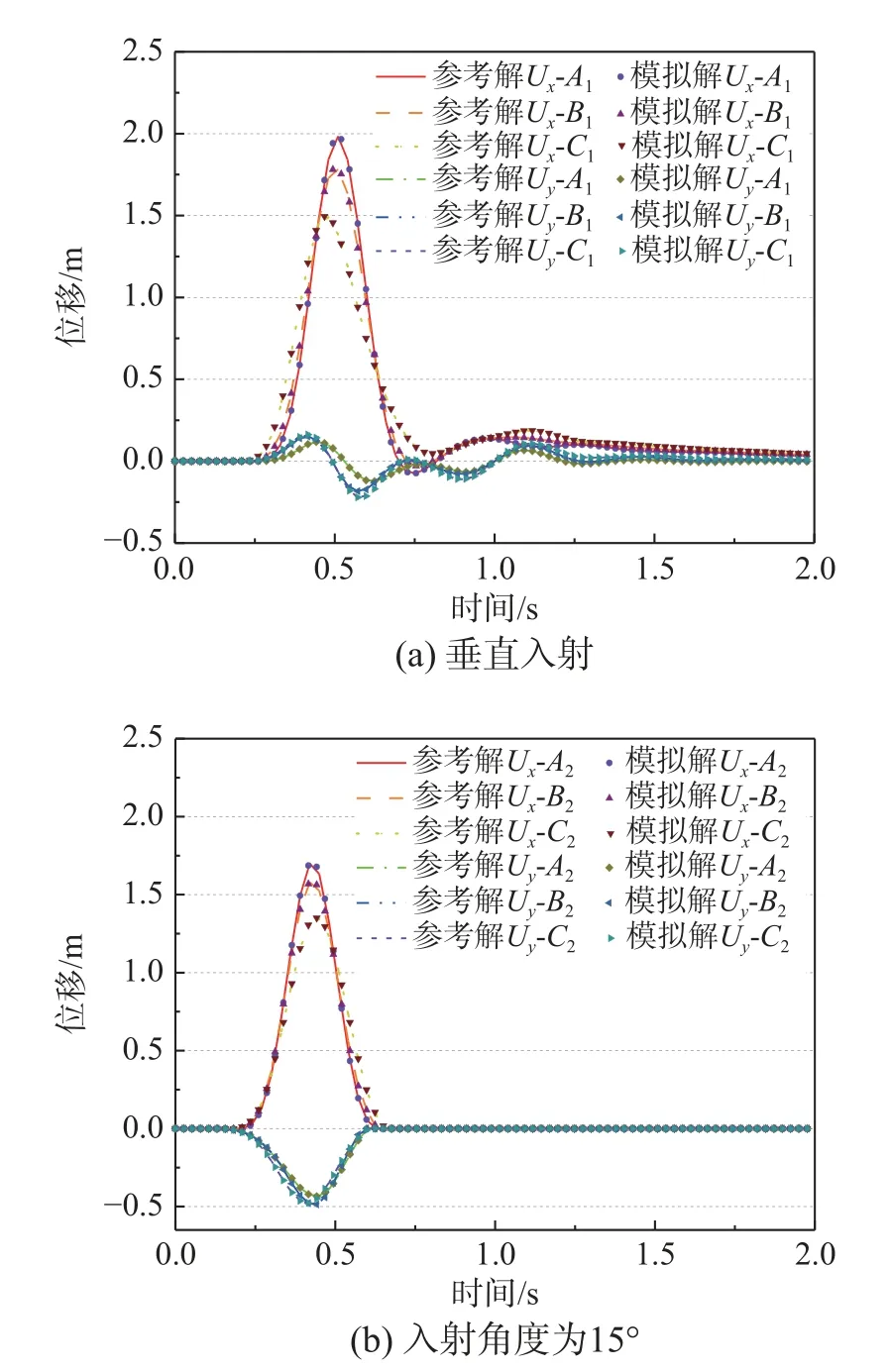
图10 SV 波入射下自由表面点位移Fig.10 Displacement of free surface under incident SV waves

2.4 结果与应用讨论

2.4.1 验证结果对比

表2 展示了本文方法与远置边界法的对比，表2 中的计算时长和文件均指第2 次节点力输入计算；实验使用的电脑型号为Intel(R) Core(TM) i7-8700 CPU @ 3.20 GHz，机带RAM 为8 G，ABAQUS为2017 版本。可以看出使用本文方法可在保证高精度的情况下有效缩短计算时长并减小结果文件存储空间，当研究范围扩展到三维空间后优势将更加明显。

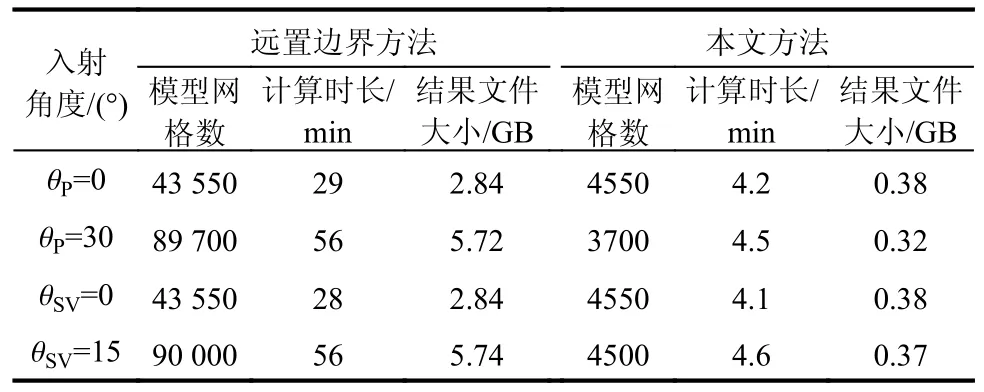
表2 两种方法的结果对比Table 2 Comparison of the two methods

2.4.2 应用分析

由于本文方法涉及的理论推导和步骤较多，可以通过每次计算后的关键点位移和波场快照等进行分步检验，确保其合理性后再继续进行。主要流程分两次输入与计算，统一以P 波入射为例进行说明。

1) 非外行波场计算及第1 次位移输入：图11(a)为P 波垂直入射时采用波场分离技术计算后，三个边界上典型位置点的输入位移时程(具体位置如图5，G1为底部边界中点)。两侧自由表面的E1、F1点的横向位移幅值分别为底部G1点的两倍，这是因为自由波场包括了入射波场和反射波场，纵向位移均为0，结果是符合规律的。图11(b)显示P 波入射角度为30°时，左边界E3点的横、竖向位移均为F3点和G3点的两倍，也是由于自由波场同时包括了入射场和反射场造成的位移幅值加倍；F3点的位移曲线同底部G3点变化趋势一样，但稍有延迟，这是由行波效应引起的，整体符合波场传播的规律。

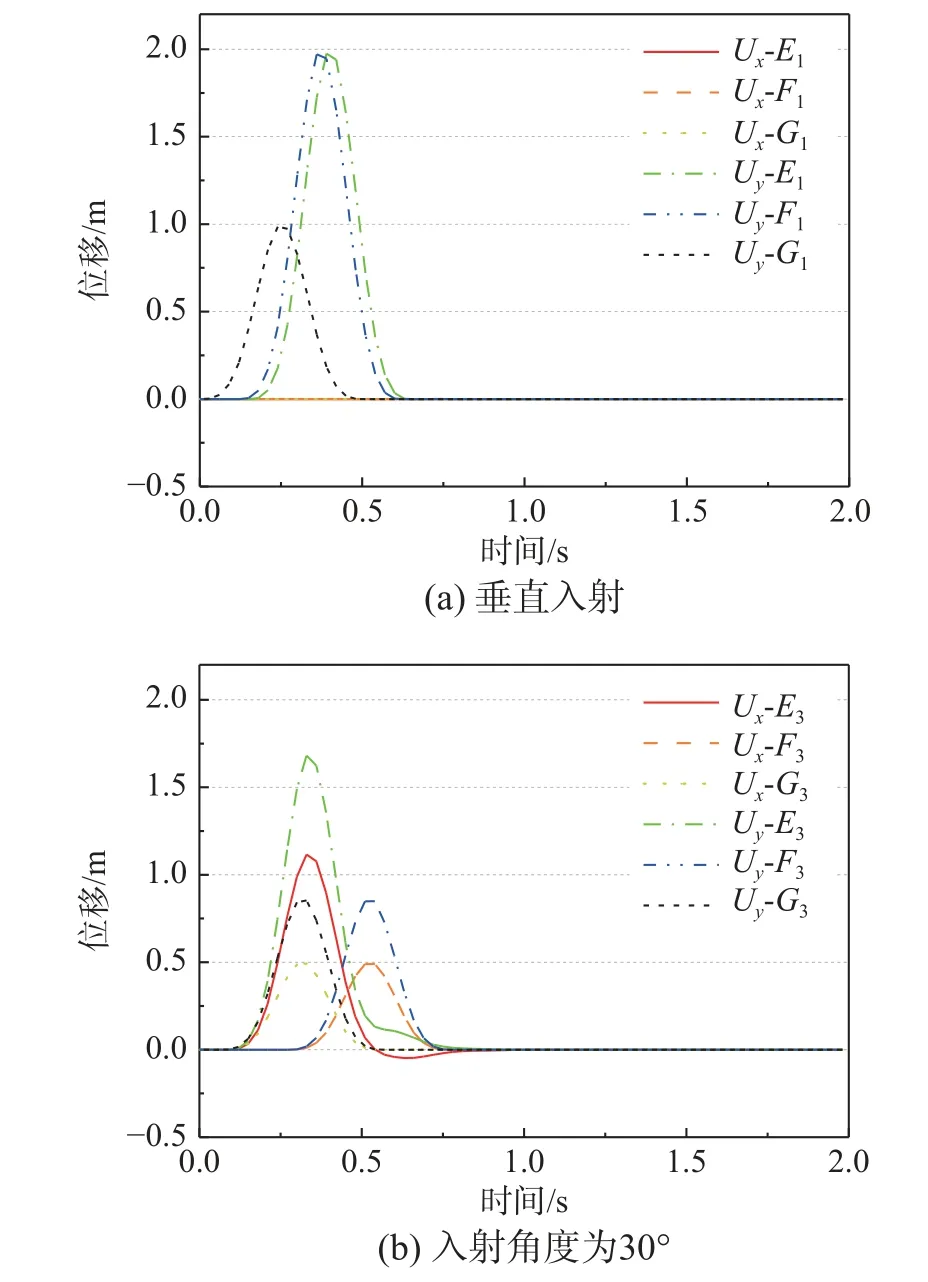
图11 场地关键点的位移输入情况Fig.11 Input displacement of key points in the site

2) 第2 次等效荷载力输入：即第1 次输入波场位移后进行有限元计算，提出各边界上的等效节点力再反向输回的过程。图12 和图13 为第2 次地震波输入后的波场快照，可以看出：开始阶段波场基本沿平面形状进行入射，证明各个边界等效节点力计算及输入的相对时间关系准确；在传播到不规则地表后波阵面形状会发生变化，可看出局部地形的影响；最后随着时间增加波场位移逐渐消失，说明黏弹性边界有效吸收了散射波。因此，不需要将边界进行远置即可获得较准确的结果。

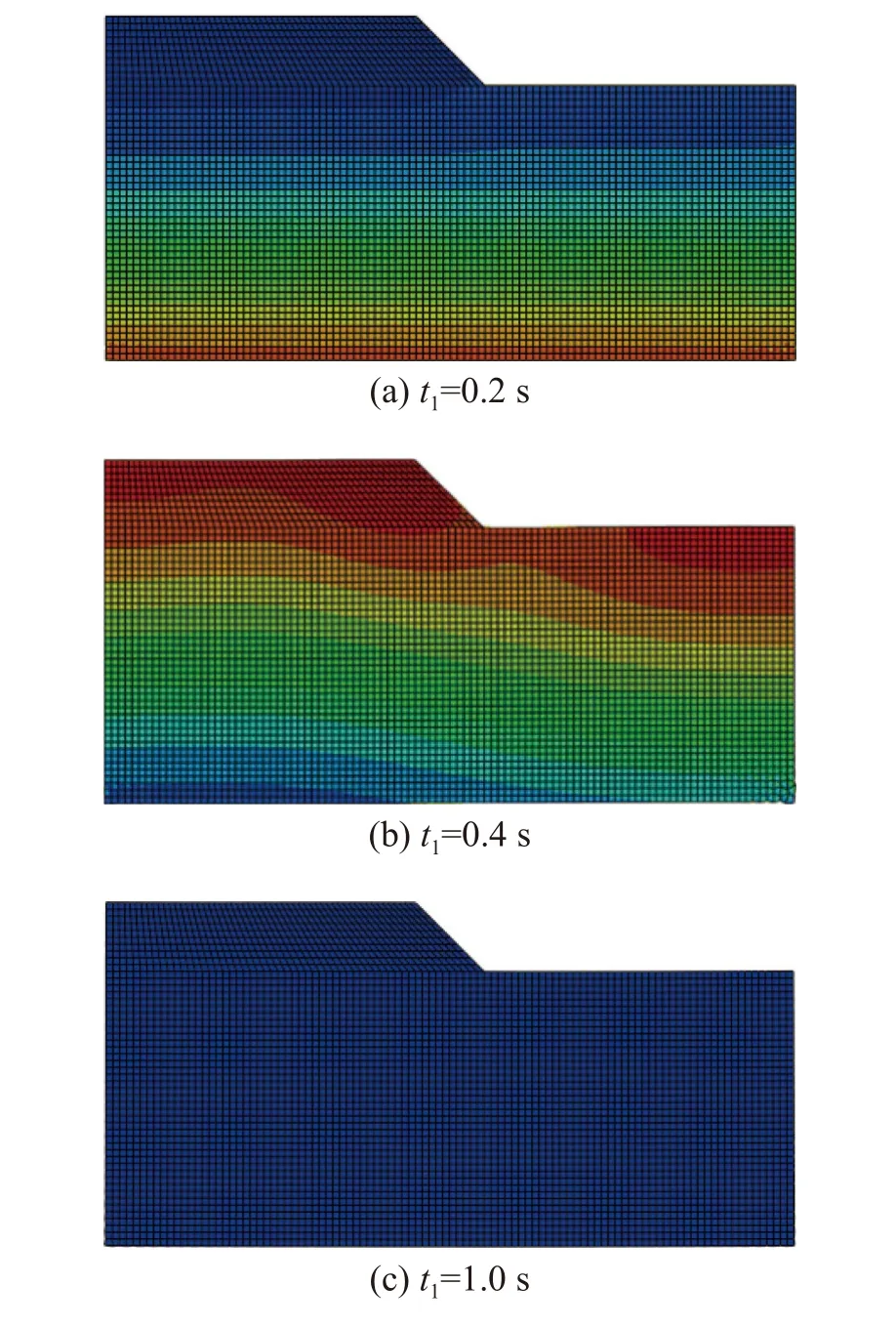
图12 P 波垂直入射时的波场快照Fig.12 Wave field snapshot of site under vertical incident P waves

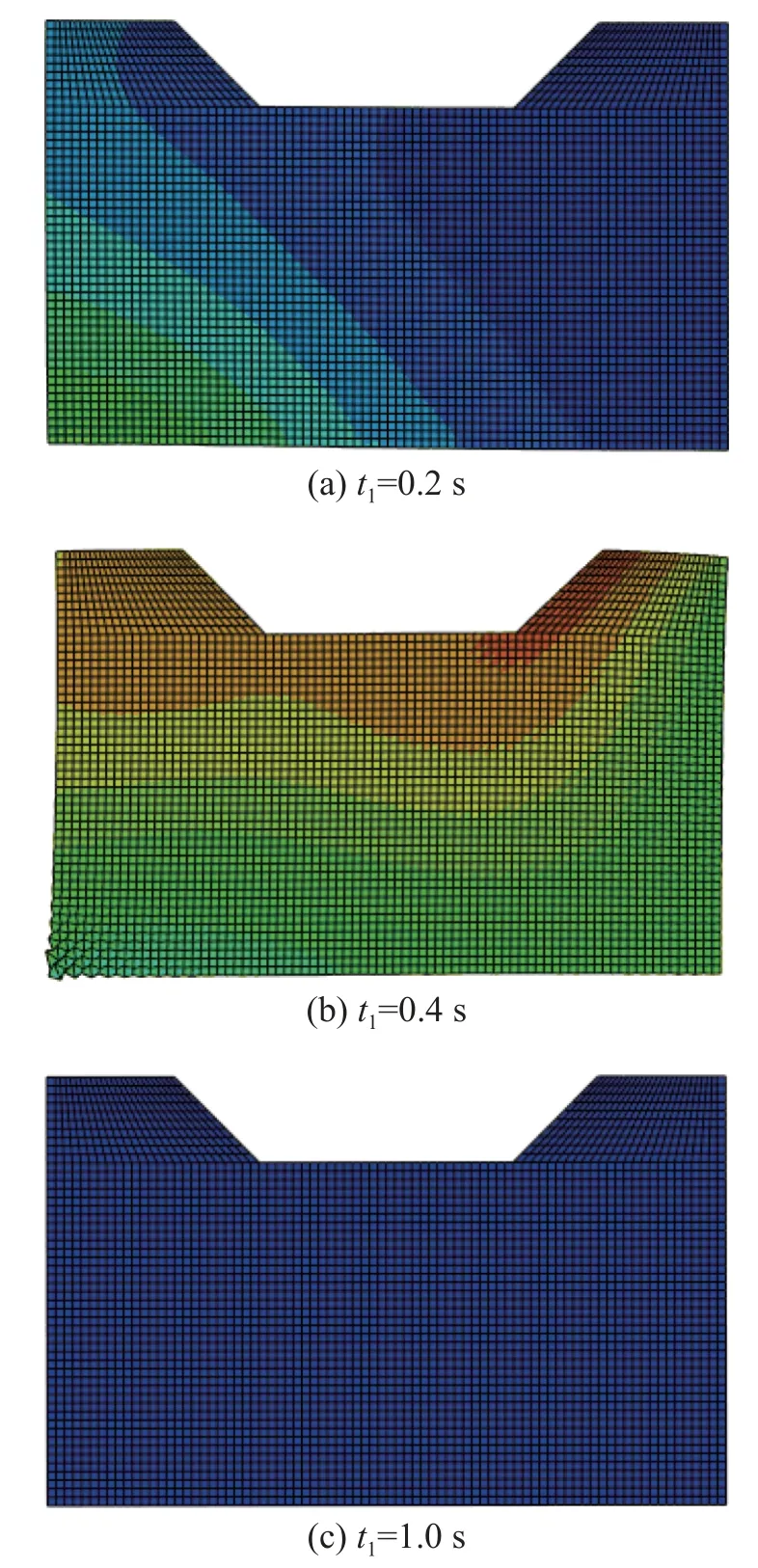
图13 P 波入射角度30°时的波场快照Fig.13 Wave field snapshot of site under P waves with the incident angle of 30°

2.5 方法对比验证与拓展

2.5.1 与频域精确解的对比

由于不规则地形的地震波场无频域精确解，故前文结果均与参考解进行对比。实际上，本方法针对大部分半空间场地是通用的，为进一步证明其正确性与精度，建立规则地形模型进行验证，规则地形地震波场的建立基于较多的假设与简化，因而有精确的解析解。

参考了文献[12]选取相应的解析方法，图14为规则地形场地的有限元模型，网格划分方式、场地模型参数、边界约束、荷载施加方式和地震波形式均与2.1 节的模型一致。选取自由表面中点C点为观测点，图15 为P 波30°入射和SV 波垂直入射下C点的位移。可以看出本文方法所得出的结果与精确解几乎吻合，验证了所提出方法的可靠性。

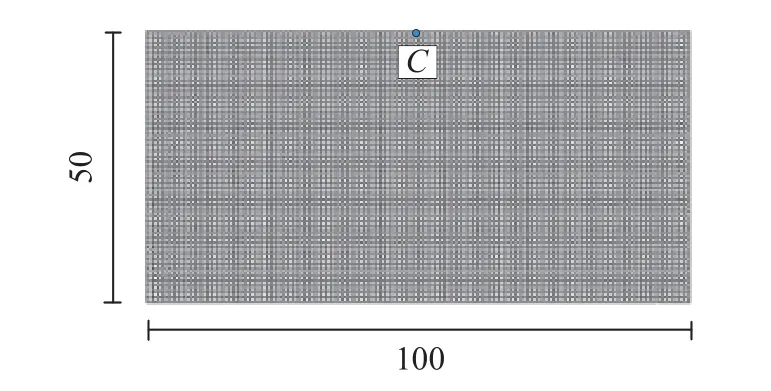
图14 规则地形场地的有限元模型 /mFig.14 Finite element model of regular terrain site

图15 地震波入射下规则场地自由表面点位移Fig.15 Displacement of free surface of regular site under seismic waves

2.5.2 与已有方法的对比

不规则地形场地的波场求解已有一些成熟的方法，选取文献[25]中的方法进行进一步对比。文献中将波场在人工边界处进行分解，用黏性边界模拟输入波场外的其余波场，并根据地基参数确定边界阻尼参数等。将此方法应用到图6 中的阶梯型场地与梯形河谷型场地模型中，分别选取了自由表面C1和C3点为观测点，图16 展示了其在P 波30°入射和SV 波垂直入射下的位移。

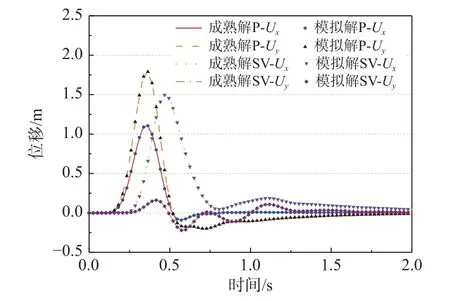
图16 地震波入射下阶梯型场地自由表面点位移Fig.16 Displacement of free surface of stepped site under seismic waves

从图16 中可以看出，本方法和文献[25]中方法得出的位移结果基本一致，证实了其在垂直入射和斜入射时波场计算均较为高效，同时本文方法相比于成熟方法而言计算节点力过程更加简单，对人工边界的限制也较低。

2.5.3 拓展应用

波场分离方法同样适用复杂的场地条件，只是当介质参数较为复杂时，入射波场和自由波场的求解难度会显著增大。为使方法推广性更强，这里以最为常见的成层场地为例，补充一下其计算思路。

成层介质自由波场的推求已有较多频域和时域的成熟方法[32-33]。而大部分文献中没有详细介绍成层地基内入射波场求解，这里推荐2 种方案：1) 频域法求解可结合传递函数法和刚度矩阵而推求；2)时域方法求解可根据几何关系[34-36]，截取地震波还未入射到自由表面前的位移时程，即可从自由波场中去除反射波场的影响，得到入射波场。

此外，更为复杂的三维真实地形条件下地震波场的构建也是后续研究的重点。

3 响应结果分析

3.1 入射角度对结果的影响

以图5(a)中的阶梯型模型为例，分别计算P 波和SV 波不同入射角度下自由表面A1点的位移响应情况。因为平面SV 波入射时存在临界入射角，一般在35°左右，因此选取SV 波入射角度范围为0°～30°，P 波入射角度为0°～90°。如图17 和图18所示，随着P 波入射角度的增大，横向位移幅值先增大后减小，大约在60°左右时达到最大；竖向位移呈现逐渐减小的趋势。但当P 波入射角度为90°时，位移呈现波动变化趋势并未完全收敛，说明本文方法对于超大角度的波动输入问题仍有一定问题需要处理。随着SV 波入射角度的增大，横向位移呈现逐渐减小的趋势但变化幅度较小，纵向位移幅值呈现逐渐增大的趋势。对于不规则地形来说，入射角度对振动响应的影响也是符合基本变化规律，且不同角度情况下位移变化幅度较大，说明对于地震波入射角度的考虑是必要的。

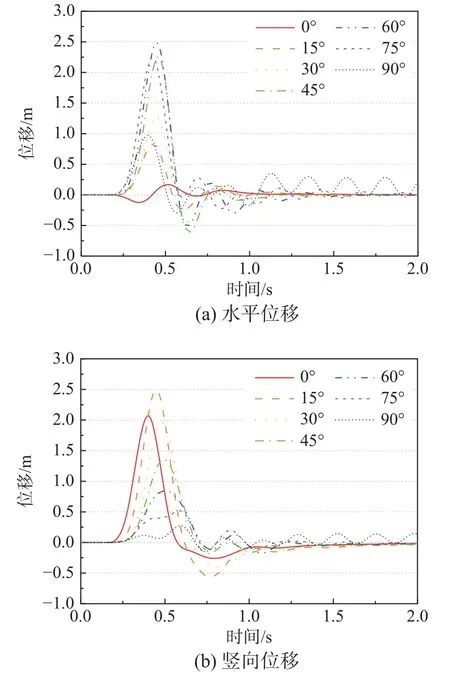
图17 P 波不同入射角度下阶梯型场地A1 点位移Fig.17 Displacement of A1 on the stepped site under P waves with different incident angles

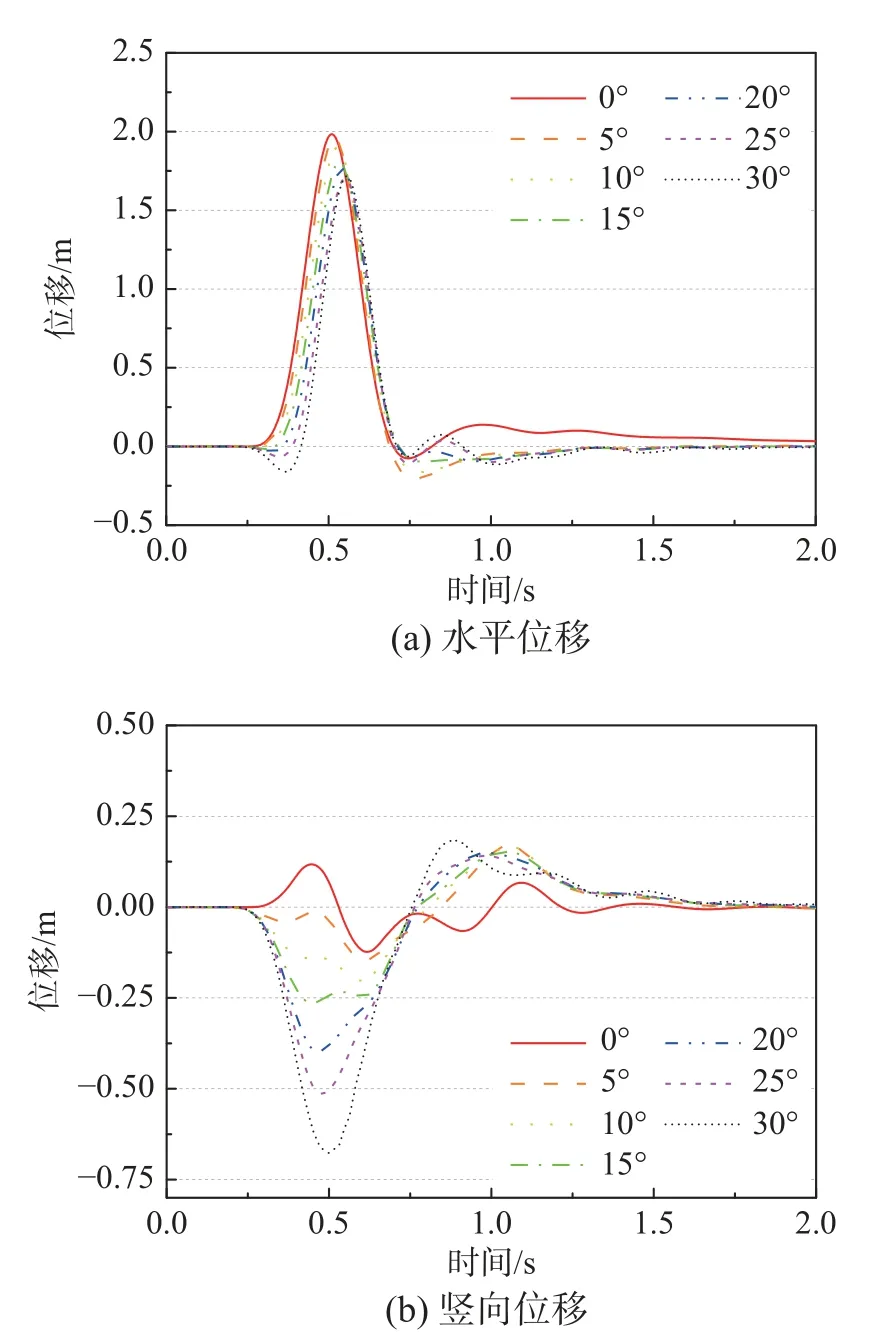
图18 SV 波不同入射角度下阶梯型场地A1 点位移Fig.18 Displacement of A1 on the stepped site under SV waves with different incident angles

3.2 局部地形对结果的影响

选用图14 中的规则地形场地作为参考，即100 m×50 m 的长方形场地，其动力参数均取为相同。表3 和表4 分别展示了P 波和SV 波入射条件下两种地形条件下自由表面A1点的位移幅值对比；其中，相差百分比的计算方法统一为(规则地形下位移-阶梯型地形下位移)/阶梯型地形下位移。由表3 和表4 可见，在两种场地条件下，位移随着地震波入射角度的变化均呈现相同的变化规律，与3.1 节的规律一致。同时可以看出局部地形条件对场地位移的影响较大，在P 波入射条件下大部分情况阶梯型场地下位移较大，SV 波入射下则相反。说明地形对地震波散射等传播规律的影响复杂多变，会随着波型和入射角度的变化而变化，在地震计算中对于地形因素的考虑也是必要的。

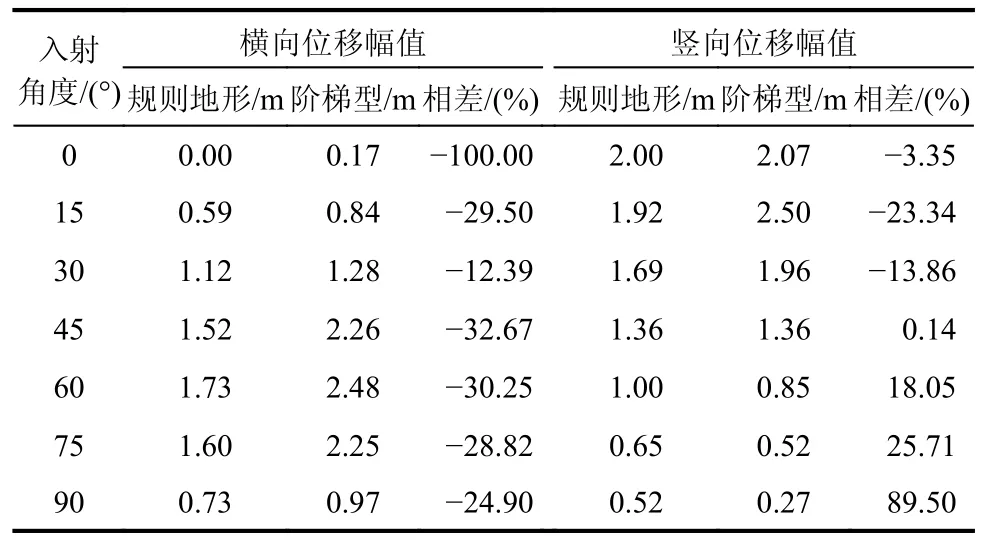
表3 P 波入射时不同地形条件下自由表面A1 点位移Table 3 Displacement of A1 under different terrain conditions when P waves incident

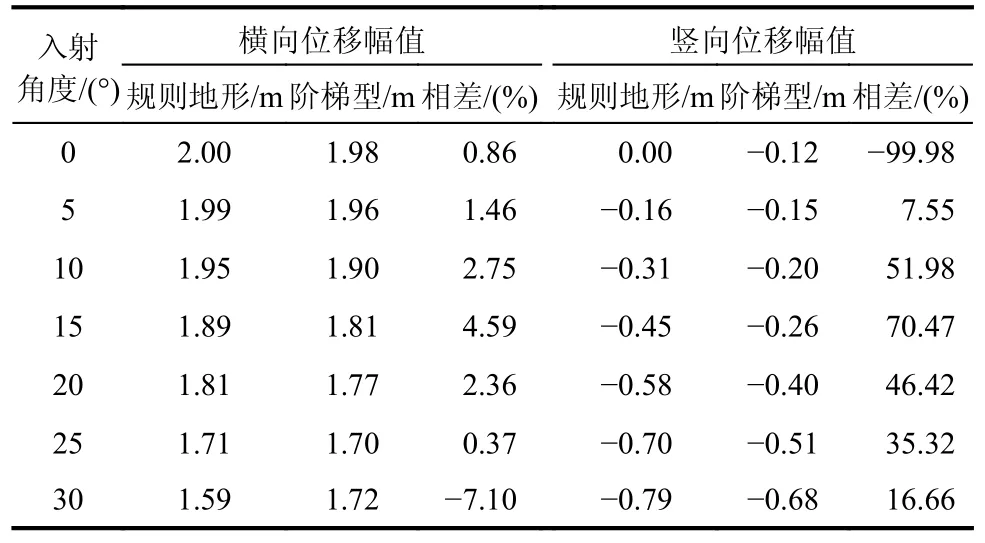
表4 SV 波入射时不同地形条件下自由表面A1 点位移Table 4 Displacement of A1 under different terrain conditions when SV waves incident

4 结论

合理的地震动输入是动力分析的必要基础，采取了解析推导结合数值模拟的手段，提出了一种基于波场分离技术和应力型人工边界的地震波场计算与输入方法，分别详细推导了地震P 波和SV 波在垂直入射和倾斜入射下的地震波场，在充分考虑到局部地形产生的散射波场的同时，采用了改进的波动输入方法实现地震波的高效输入。此外，对比分析了多组不同入射角度下的规则和不规则地形的场地反应情况，主要得到了以下结论：

(1) 通过与远置边界法得到的自由表面位移的参考解进行对比，证明了方法的精确度与高效性，且适用于多类不规则地形条件的场地以及不同的地震波型和入射角度。

(2) 所采用的改进的波动输入法，极大简化了等效节点力计算，将地震波输入的重难点聚焦于场地自由波场和入射波场的计算，使得所提出的方法易于推广至三维场地以及成层地基情况。

(3) 地震波的入射角度变化对不规则场地地表位移响应影响较大，自由表面点随着P 波入射角度的增大，横向位移幅值先增大后减小，竖向位移呈现逐渐减小的趋势；随着SV 波入射角度增大，横向位移呈现逐渐减小的趋势，纵向位移规律相反。整体变换规律与规则场地条件下的相一致且符合实际。

(4) 不规则地形条件对场地的地表位移响应也有较大影响，地震波通过局部地形时传播路径会发生变化并产生额外的散射波场，因此，其振动反应相较于规则场地有明显不同，并同时受到地震波型和入射角度等的影响。

所提出的方法和得出的规律性结论可为不规则地形上的振动响应分析提供手段，后续研究将进一步聚焦于三维真实地形条件下地震波场的构建与输入方法改进提升。