圆盘形压电双晶片结构发电特性建模及仿真研究∗

张旭东 张玮东 柴晓冬 彭乐乐 郑树彬 叶智杨

（1.上海工程技术大学城市轨道交通学院 上海 201620）（2.上海地铁维护保障有限公司车辆分公司 上海 200031）

1 引言

在我们周围环境中振动能量广泛分布，收集环境中的振动能量转化为电能是实现诸多无线智能传感器能源自供给的最要途径［1～4］，由于压电材料所具有较大的机电耦合系数及较高的能量转化效率，压电振动能量收集器被广泛应用。轨道车辆运行过程中所产生的振动，具有瞬时冲击较大的特点［5～6］，所以发电效率高、与车辆振动频谱高度适配的压电结构是实现安装在轨道车辆轴箱处智能传感器自供给的技术要点。

目前国内外学者在压电振动能量收集器的压电材料、压电结构、动力学模型和机电耦合模型等维度进行研究。由于压电材料作为能量转化器件，其直接影响到了振动能量到电能的转换效率［7～10］。Wen Cheng 等针对冲击载荷下温度对压电陶瓷机电响应及输出能量的影响［11］。丁维高等基于哈密顿原理，建立了压电曲梁机电耦合偏微分方程［12］。相对于常用的单端式悬臂梁［13］，圆盘形压电双晶片结构具有抗冲击性强、不易碎及发电效率高等优点［14～16］，其适用于振动强烈且瞬时冲击大的环境。

本文针对可适用于较大冲击载荷环境下的圆盘形压电双晶片结构，基于欧拉-伯努利理论建立了其固有频率模型，利用辛几何方法得出压电梁挠度振型表达式，通过基尔霍夫定律推导出输出功率模型，研究了结构参数与固有频率及发电特性之间的关系。最后通过理论值计算以及COMSOL 仿真分析，验证了模型的准确性。

2 圆盘形压电双晶片结构建模

2.1 圆盘形压电双晶片结构频率响应模型

圆盘形压电双晶片结构安装在轨道列车走行件上的能量俘获器中。在轨道列车运行过程中，载体受到振动激励，上下质量块受外界惯性力的作用而产生垂向机械振动，从而使压电陶瓷发生形变产生电荷。图1（a）为圆盘形压电双晶片结构图，该结构由金属基底、压电陶瓷及质量块组成。

圆盘形压电双晶片结构截面图如图1（b）所示，设压电陶瓷直径为Rs，厚度为Ts，金属基底直径为Rp，厚度为Tp，质量块质量为mz。以固支梁几何边界点为原点建立坐标系。

固支端A 与固支端B 对梁作用的弯矩分别为MA、MB，垂直支撑力分别为FA、FB。梁的变形微分方程为

其中，ω1和ω2分别表示梁在中间载荷作用点左右两侧的变形挠度，E为梁的弹性模量，I为梁截面的惯性矩。

力与弯矩之间的平衡关系为

联合式（1）、（2）、（3）、（4）解得变形表达式为

根据材料力学：

圆盘形压电双晶片结构的等效弹性模量为

圆盘形压电双晶片结构的惯性矩为

结合式（8）、（9），因此可以得到圆盘形压电双晶片结构的频率响应模型为

2.2 圆盘形压电双晶片结构输出功率模型

在集中载荷q(x,y,t)作用下，根据瞬态平衡条件，得圆盘形压电双晶片结构受迫振动的微分方程［17］：

根据挠度函数正交性以及杜哈梅积分计算整理可得圆盘形压电双晶片结构的挠度为

发电梁受到外力作用下相对于平衡位置的相对位移为ω(t)，当外界载体振动时，设固定载体运动位移为y，(t)为固定载体的激励加速度，从而建立系统运动微分方程：

设C为压电等效夹持电容，α为压电等效力压转换因子，V为压电输出电压，R为外接负载，基于基尔霍夫定律可列出压电悬臂梁KCL方程：

可以得到外界激励加速度幅值yM表示的输出功率表达式：

3 仿真验证

3.1 模型验证

为验证圆盘形压电双晶片结构频率响应模型的正确性，利用COMSOL有限元软件构建了圆盘形压电双晶片结构仿真模型如图2所示。

图2 圆盘形压电双晶片结构仿真图

该模型由金属基底、上下压电陶瓷以及上下质量块组成。选用铜为金属基底材质，PZT-5H 为压电陶瓷材料。其中模型各参数如表1 所示。设置激励加速度为1g，采用步长为0.2Hz，范围为0～1000Hz 之间进行扫频以获取圆盘形压电双晶片结构各阶谐振频率的大小。

3.2 验证结果

在COMSOL 软件中进行仿真得到圆盘形压电双晶片结构前六阶振型如图3所示。

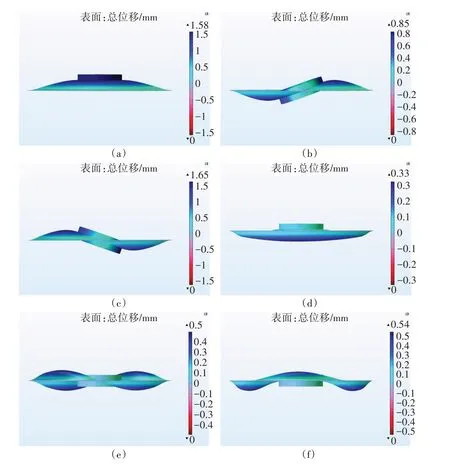
图3 圆盘形压电双晶片结构前六阶振型

图3（a）～（f）依次为发电梁前六阶振型图，其中一阶谐振频率为69.5Hz，二阶谐振频率为219.34Hz，三阶谐振频率为225.51Hz，后三阶谐振频率分别为742.03Hz、794.33Hz、798.22Hz。结合前六阶振型图可以看出，该梁第二、三及五、六阶振型基本一致，谐振频率数值接近。经COMSOL仿真软件对模型进行特征频率研究得到圆盘形压电双晶片结构在前六阶输出电压的峰值如图4所示。

图4 前六阶输出电压峰值

由图4 可以得出，圆盘形压电双晶片结构输出主要频段在二、三阶处。通过式（15）计算出圆盘形压电双晶片结构在二、三阶处输出功率理论值，并得到峰值电压值。通过理论值与仿真值，计算其相对偏差。圆盘形压电双晶片结构在二、三阶处仿真数据、实验数据与理论数据如图5（a）、（b）所示。

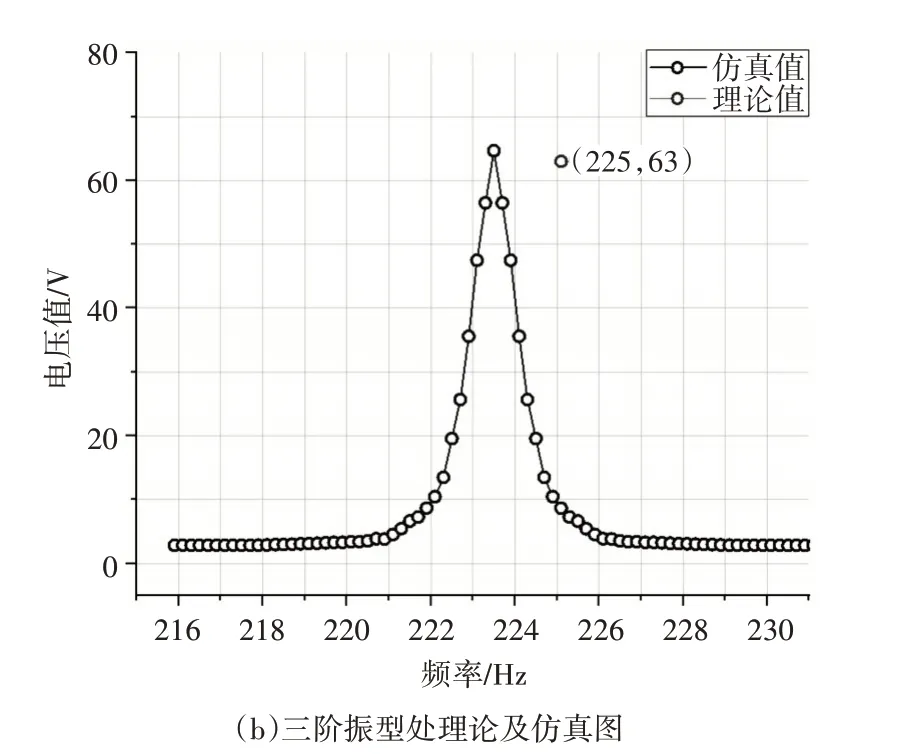
图5 二、三阶振型处理论及仿真图

从图5（a）、（b）可以得出，圆盘形压电双晶片结构理论值与COMSOL 有限元仿真模型得出的仿真值在谐振频率以及输出电压峰值方面数值非常相近。其中在二阶振型处频率相对误差为1.94%，输出电压峰值相对误差为2.09%，在三阶振型处频率相对误差为1.14%，输出电压峰值相对误差为2.67%。综上所述仿真及实验，可以得出，圆盘形压电双晶片结构谐振频率模型及输出功率模型误差值均在3%以内，证明了模型的正确性。

4 结语

为获取圆盘形压电双晶片结构的发电特性，本文构建了频率响应及输出功率模型，通过仿真验证了模型的正确性，可以得到以下结论：通过对圆形压电双晶片发电梁受力变形分析，推导出复合结构等效刚度及等效惯性矩，得到了固有频率模型及输出功率模型，确定了其主要结构参数。通过COMSOL 仿真结果，得到圆形压电双晶片发电梁在二三阶处输出峰值电压为别为87.6657V 和64.6657V，即其主要输出频段在二、三阶振型处。根据圆形压电双晶片发电梁理论值及仿真值，其相对误差均小于3%。