基于双环设计的PD 垂直起降飞行器轨迹跟踪控制∗

刘栩粼 胡德清

（四川信息职业技术学院电子与物联网学院 广元 628000）

1 引言

垂直起降飞行器［1］（vertical taking-off and landing aircraft，VTOL aircraft）不仅具备较高的巡航速度，还具备不受跑道限制就能自由起飞降落的特点，除军事用途外，在媒体及娱乐、检查监控、公共安全、农业优化等商业或非商业领域，也有着十分广阔的应用前景。但由于VTOL 飞行器是集欠驱动、非最小相位于一身的非线性系统［2］，不难发现具有良好的轨迹跟踪控制性能是保障VTOL 飞行器能够稳定运行的重要因素之一。因此，研究其轨迹控制方法一直是VTOL 飞行器产业发展的重要热点之一［3］。

伴随着飞行控制技术的发展，新技术与PD 控制技术相结合的控制方法在VTOL 飞行器控制中得到了大量的应用［4］，比如，为了保障飞行器稳定飞行，文献［5］开发并优化一种基于高阶观测器的鲁棒动态滑膜控制方法，以缓解VTOL 颤振现象所引起的不稳定问题；又比如，针对VTOL 无人机存在下降速度和下沉率较大的问题，文献［6］再次引入鲁棒伺服设计了VTOL 无人机着陆控制方法，减缓了无人机着陆的瞬时速度，进而实现其安全稳定地着陆［6］；宋志强等［7］基于线性PD 控制方法，通过调整内外环增益系数，设计并解决了无人机着陆控制。张妍等为了解决VTOL 的轨迹跟踪控制问题，简化控制系统的设计过程，提出了一种基于双闭环PD 控制的轨迹跟踪控制方法，满足了飞行器能够快速准确跟踪到给定轨迹的需求［8］。

本文主要以垂直起降飞行器为研究对象，建立其线性数学模型［9～11］，再基于前馈补偿对垂直起降飞行器控制器进行PD控制方法设计，其次，将轨迹跟踪系统分为内外两个控制环路，最后进行Matlab/Simulink 的仿真实验验证。研究结果表明，基于双环设计的PD控制方法使得垂直起降飞行器性能指标较好，能补偿控制系统所受到的内外干扰，提高控制系统的稳定性。

2 垂直起降飞行器模型

通常，垂直起降飞行器的数学模型是由6 个物理参数来描述［12～14］，即横滚角ϕ、横向位移X、垂直位移Y以及这3 个物理量取导所得的横滚角速度、横向速度和垂直速度。在不考虑外界干扰的情况下，根据牛顿第二定律，可得到垂直起降飞行器的动力学模型如下所示。

上式中，T表示的是飞行器底部推力力矩，TL表示的是横滚力矩，这两个物理量是为了用来直观地描述VTOL 飞行器的控制输入。ζ0则是T和TL之间的耦合系数；J为绕纵轴的转动惯量。令：

其中，u1为飞行器底部推力力矩、u2为飞行器横滚滚动力矩；结合式（1）、式（2），可得到垂直起降飞行器的动力学模型为

又令：

其中，τi(t)为外界干扰项；x1、x2、y1、y2和ω分别代表飞行器的横向位移、横向速度、垂直位移、垂直速度、横滚角速度。忽略耦合和扰动带给VTOL飞行器的影响，结合式（4），可将动力学模型式（3）化简如下：

3 垂直起降飞行器控制器设计

从模型式（5）中不难发现，VTOL飞行器是一个欠驱动控制系统［15］，难以对3 个物理输出量同时进行跟踪。因此，本文提出一个合理的控制方案：跟踪横向位移xd和垂直位移yd，同时保证横滚角ϕd的角度及其角速度［13］。其VTOL 控制系统结构图，如图1所示。

图1 基于双环设计的PD控制

在接下来的整个设计过程中，选取工程方法对双闭环系统进行稳定性分析，即保证外环控制增益远小于内环增益的控制方法。

3.1 位置控制律的设计

通过设计位置通道控制力u1，实现VTOL 飞行器横向和垂直轨迹跟踪［15～18］。根据工程稳定性分析方法、式（2）、式（5）可得到飞行器二维位置状态的模型为

取v1=-u1sinϕ，v2=u1cosϕ，可得

采用PD控制方法设计第一个横向位移x子系统的控制律为

同理，采用基于前馈和重力补偿的PD 控制方法对第二个垂直位移y子系统设计控制律：

因此，基于补偿的PD 位置控制各参数如表1所示。

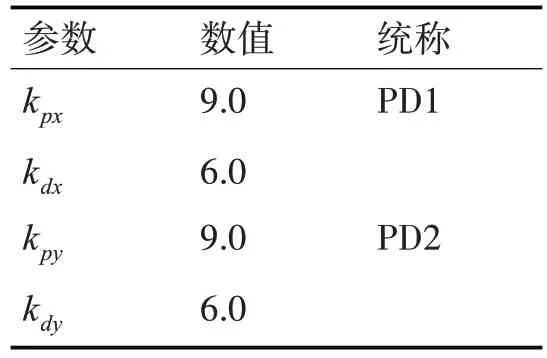
表1 PD位置控制参数表

3.2 虚姿态角度控制律的设计

接下来，设计横滚角通道控制力u2，以实现VTOL 飞行器姿态角度轨迹跟踪［19］。由式（5）可得描述横滚角及其角速度状态的模型为

取跟踪误差为e=ϕ-ϕd，ϕd为横滚角目标值。设计基于前馈补偿的PD控制律为

对式（11）中的ϕd求导，本文采用以下三阶积分链式微分器来实现一次导、二次导：

其中，x1、x2分别为横滚角速度目标值、横滚角加速度目标值。需要注意的是，为了抑制微分器出现的峰值现象，在初始时间段0 ≤t≤1，取：

因此，基于补偿的PD 姿态控制参数如表2 所示，控制方案如表2所示。

4 闭环系统设计

上节所设计的横向位移PD 控制律、垂直位移PD 控制律和横滚角PD 控制律，能使VTOL 飞行器具有良好的轨迹跟踪状态，其全局控制系统结构图，如图2所示。

取u1方向为正方向，由式（3）、式（8）和式（9）可得控制律：

上述闭环系统是由内环姿态子系统、外环位置子系统构成的控制系统，采用了双环控制方法来设计PD 控制律。外环产生一个中间指令信号ϕd传递给内环系统，内环控制不仅能对ϕd信号进行跟踪，并且能将外环产生的误差e进行消除［20］。

5 仿真结果

为了验证基于双环设计的PD 控制器对VTOL飞行器的轨迹跟踪性能，在Matlab/Simulink 环境下进行了数值仿真实验。

结合VTOL 的数学模型式（5）、PD 控制律式（11）和式（14）。取g=9.8m/s2、微分控制器参数ζ=0.01、k1=9.0、k2=k3=27.0、初始状态均为0、目标轨迹取直径为2m 的圆，即xd=sint、yd=cost。并且，在PD 控制律的作用下，取外环控制器增益远小于内环控制器增益的方法，来保证闭环系统的稳定性。最后，仿真结果如图3～6所示。

图3 两种位置及速度的跟踪过程

从上图分析可知，VTOL 飞行器在控制律式（8）、式（9）的控制下，其横向位移及横向速度均在1.5s 内就可迅速跟踪到位；而VTOL 的垂直位移和垂直速度也均在0.2s 内就能快速准确地跟踪给定位置轨迹。

从图4 可知，在控制律式（11）的控制下，VTOL飞行器的横滚角及其角速度均在0.5s 内就能快速准确地跟踪给定姿态轨迹。不难发现，所设计的控制算法确实能实时调整内环增益系数，以确保闭环控制系统的稳定性。

图4 横滚角及其角速度的跟踪过程

图5 两个通道控制力的跟踪过程

从上述两个通道跟踪结果可以得出：在0～1.5s内，横滚通道的控制量输入变化陡度大，但两种通道的控制力均能在1.5s内收敛到位。

从图6 可知，本文提出的控制方法能够使得垂直起降飞行器的实际飞行轨迹快速且准确地跟踪上目标轨迹，满足欠驱动系统的轨迹跟踪要求。

图6 轨迹跟踪

6 结语

在存在外部未知扰动的情况下，基于双环设计的PD 控制器通过控制VTOL 飞行器增益系数，即设计横滚角的PD 控制律时，选择较大PD 增益，以确保外环收敛速度远小于内环收敛速度，且横滚角及其角速度均有界。从仿真结果中可知，VTOL 飞行器不仅在横滚角和位置的调节时间上用时较短，并且能使得VTOL 按照期望的轨迹飞行，较好地补偿了控制系统所受到的干扰，提高了系统的稳定性。