基于距离异常点的机械比能评价储层物性研究∗

李 龙 管 洁

（东北石油大学计算机与信息技术学院 大庆 163318）

1 引言

钻井过程中，扭矩和钻压会在钻进过程中出现异常点，机械比能模型［11］容易受到钻压、扭矩等敏感因素的影响，因此有必要对影响机械比能评价的因素中的异常数据进行检测，提高数据以及评价的准确性。传统的基于统计的异常数据的挖掘算法大致有3σ准则、四分位（箱线图）等。而基于距离的异常数据挖掘算法原理较为简单，使用方便，在数据集分布均匀的情况下，检测效果较好。所以本文应用基于距离的异常点检测算法，对机械比能评价模型进行补充，使得评价结果更加准确，这对于储层物性评价具有重要意义。

2 传统基于统计学的异常值检测方法介绍

在统计学中，离群值是不属于特定总体的数据点，是远离其他值的离群值。离群值不同于其他结构良好的数据。

2.1 3σ准则

随机误差的分布密度为

式中：δ为随机误差；若不考虑系统误差，则δ=x-μ，是的数学期望；μ为X 的数学期望；σ为随机误差δ的标准差，也是测量总体X的标准差。

由分布密度f(δ)的定义可知，δ在δ1和δ2之间内取值的概率应为相应区间上密度函数的积分，即

对于给定的误差界限±δ，即可根据由概率积分求得值出现在［-δ，+δ］范围内的概率。随机误差在范围内出现在［μ-3δ，μ+3δ］的概 率0.9973，出现在［μ-2δ，μ+2δ］的概率0.9545。

3σ标准是假设一组测试数据只包含随机误差，计算并处理得到标准差，并按一定概率确定区间。认为超出该区间的误差不属于随机误差误差，而属于粗差，应剔除含有该误差的数据。判别处理的原理和方法仅限于正常或近似正态分布样本数据的处理［18～19］。其前提是测量数量足够大（样本>10）。当测量次数较少时，用该准则消除粗差是不可靠的。

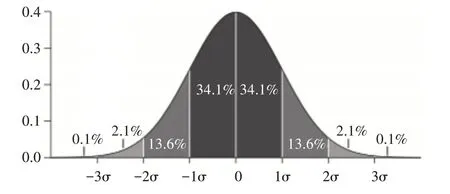
图1 3σ标准图

可以认为几乎所有的Y值都集中在（-3，+3）范围内，超过这个范围的概率小于0.3%，因此，如果你有任何数据点超过标准差的3 倍，那么这些点很有可能是异常值或离群点。

2.2 四分位（箱线图）

箱形图是数字数据通过其四分位数形成的图形化描述。这是一个很简单但是很有效的方法来显示异常值。想一想上面和下面的触须就是数据的分界线。在上面或下面的任意一任何高于上触须或低于下触须的所有数据点，都可以看作是离群点，也可以看作是孤立点。

四分位间距（IQR）的概念被用于构建箱形图。IQR 是统计学中的一个概念，通过将数据集分成四分位来衡量统计分散度和数据可变性。简单来说，任何数据集或任意一组观测值都可以根据数据的值以及它们与整个数据集的比较情况被划分为四个确定的间隔。四分位数会将数据分为三个点和四个区间。

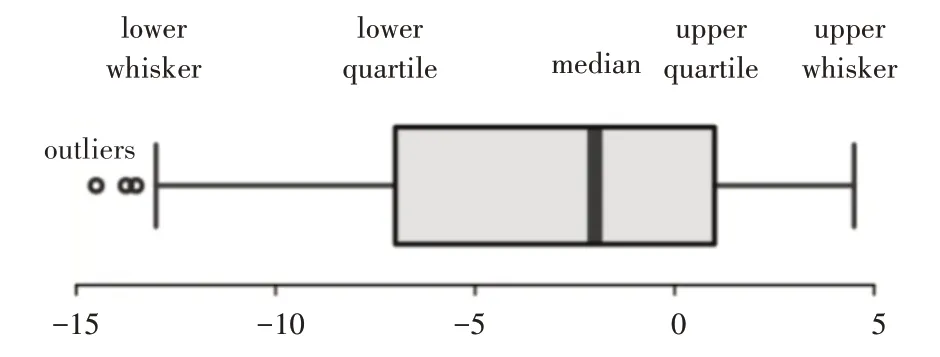
图2 箱线图

四分位间距对定义离群点非常重要。它是第三个四分位数和第一个四分位数的差（IQR=Q3-Q1）。在这种情况下，离群点被定义为低于箱形图下触须（或Q1-1.5·IQR）或高于箱形图上触须（或Q3+1.5·IQR）的观测值。

3 基于距离的异常点检测

Knorr和Ng［1］本文首先采用一种新的算法来发现异常值。他们觉得异化了这些点如下所示：在一个数据集中，有一个或多个数据点与另一个或多个一定的门限D，本质上就是视异常为在D区域中近乎不存在的邻近的那一点。

表1 参数及意义

3.1 检测属性的选取

在数据集中，离群点并非在每一个属性中都存在，只有在某些属性中才会出现离群点。总地来说，选择这些研究价值属性是该领域专家的责任。然而，针对终端操作员缺乏相关专业知识，难以从海量数据中筛选出对数据稳定性有较大影响且有研究价值的问题，提出了属性隶属度概念。它可以反映出每一种属性的检测结果。即使在没有域专家的情况下，终端操作员也能根据每一种属性的“属性从属程度”来选择最适合的探测属性。

属性隶属度：数据集中任何数据的任何属性，都有一个相应的数字μ（ω），也就是这个属性的属性隶属度，μ（ω）即该属性的编号，表示为

当属性的μ（omega）值较大时，属性值波动较大，检测值较高时，则更容易被检测到。μ（omega）值较小时，属性值波动较小，探测值较低，容易被忽视。

3.2 改进距离度量

针对由于数据分布不均匀而造成的检测准确率不高的问题，对距离测量进行了改进，以Minkowski距离作为例子，表示为

其中λk定义为

对于非均匀性数据，基于公共距离的离群点检测方法往往效果不佳［2～4］。当数据点分布于稠密和稀疏两种情况下，由k 个最近邻点组成的局部区域具有区分性。

根据传统的基于距离的离群点检测算法，能改变原始的正态［18～19］范围，将频繁的数据点标记为离群点［5］。

图3 显示了抛物线形状的非均匀分布数据集。假定A 点是s 数据集中的一个异常点，B 点是s数据集中的一个正常点，如果B 点到K 个最近邻的距离之和大于A 点到K 个最近邻的距离之和，传统的基于距离的算法可能会将B 点视为一个异常点并将其视为点A为正常量数据点［6～7］。

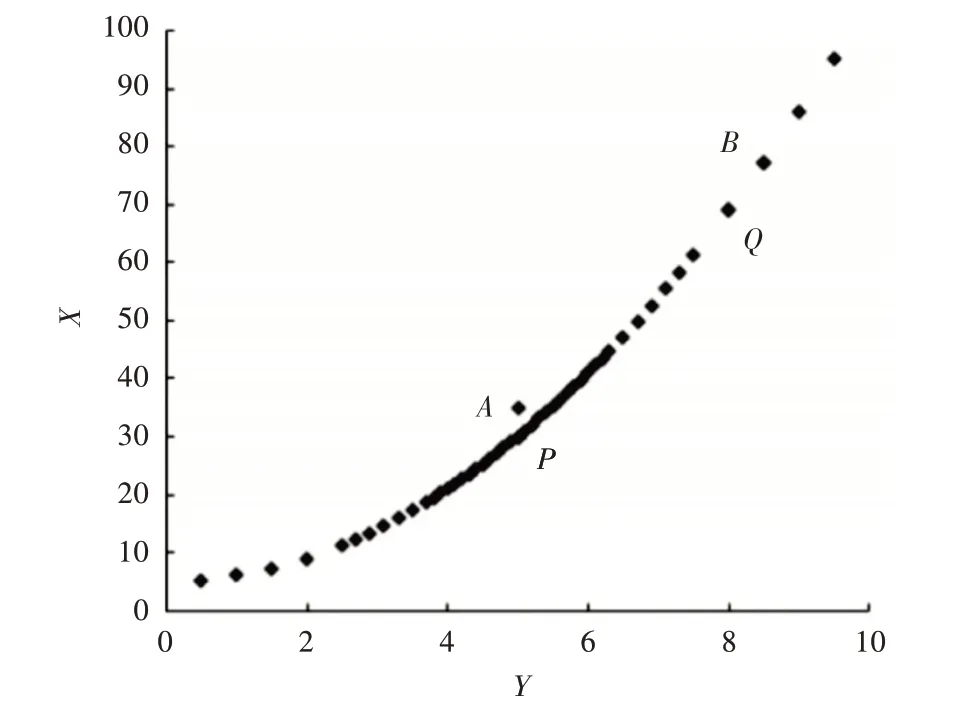
图3 不均匀分布的散点图

设dA(k)

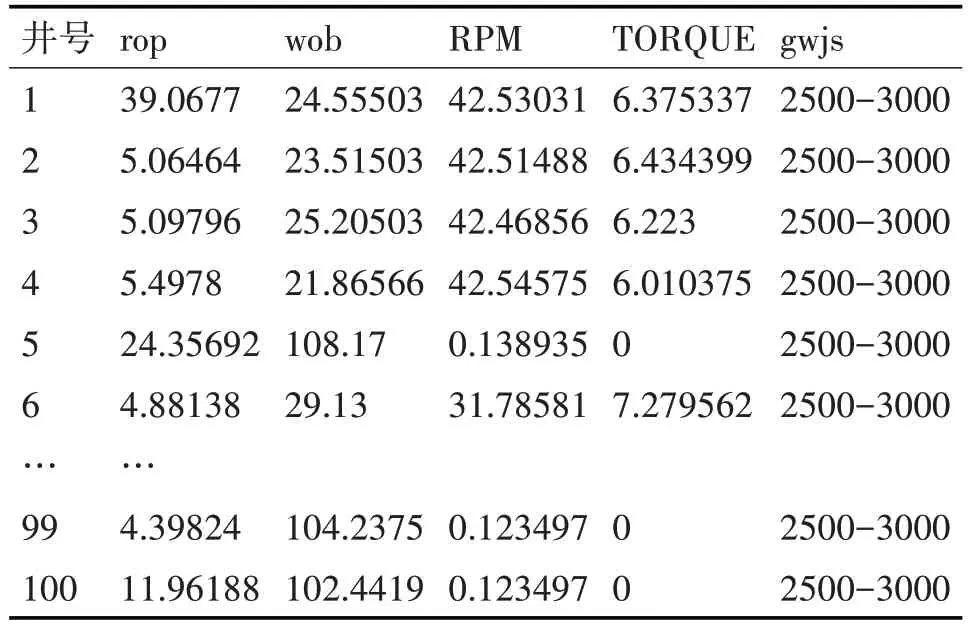
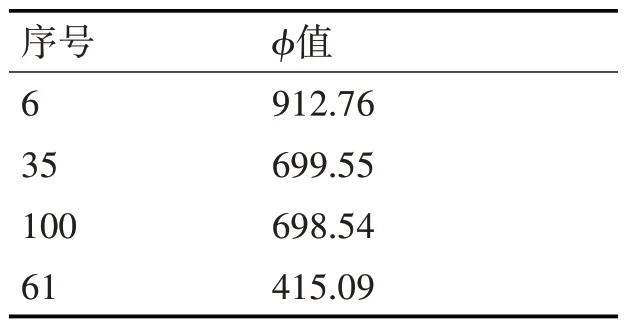
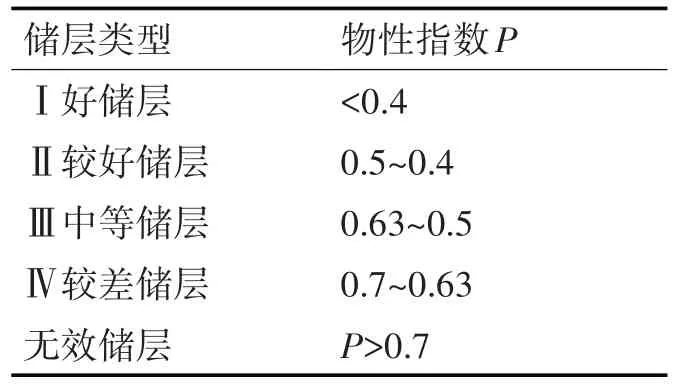
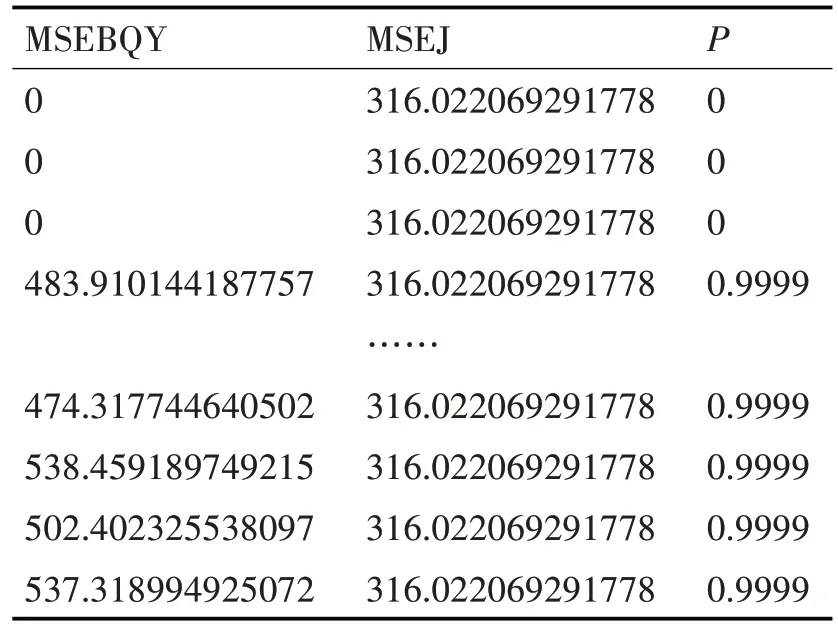
3.3 基于距离的异常点检测算法

步骤如下所示。

步骤1：假设该数据经过了标准化，则会对该数据集的第一个数据和dij其它数据之间的距离进行比较。

步骤2：该数据点与K 个最接近的邻域（K）的距离的总和由步骤1获得。

步骤3：计算K，找出数据点与其他数据点之间的改进距离dMij，kdij。步骤4：循环步骤1 到步骤3，直到计算出数据集中所有数据点的dMij，形成一个主对角线元素为0的对称矩阵P：

这个方法是这样来描述的：1）在一个矩阵P中，每一个元素都代表两个点的间距。举例来说，d12M代表了一个点与一个点的间距。2）作为对矩阵P 中第ϕi行元数之和进行评估的一个重要指标，该指标的数值愈大，则该指标的数值愈大，则该指标的数值愈小，则该指标与其它指标的距离愈大。那就意味着，这里的情况要比别的地方更加反常。

4 实验设计

实验选取100 组解释评论数据进行离群点监测，每条记录包含5个属性（rop，wob，RPM，TORQUE，gwjs）。通过怎么算每一个属性的值，选值最大的两个属性。经筛选后的数据集如表2 所示。

表2 部分数据集

在实验中所用的距离度量为q=2 时的Minkowski 距离进行计算，即当k=30 时，距离和矩阵P为

由矩阵P 可计算出100个ϕ值，对ϕ值进行降序排列，设用户期望的异常值为4，则可得到四个异常点，如表3所示。

表3 异常点检测结果

表4 机械比能分级

表5 实验结果

根据输出结果，若数据点的距离之和为递减顺序，那么可以将前四条记录，也就是序号为6、35、100、61 的数据与其他点的距离之和最大，从而判断为异常数据。

5 储层物性评价过程

5.1 数据归一化

数据归一化处理：使用最大最小值归一化方法［17］，公式如下：

按段寻找相应的最大值max 和最小值min，则机械比能［14］的归一化如下：

5.2 物性评价

1）钻压和扭矩做功的机械比能模型［11］：

式中：WOB 为钻压［16］，N；Ab 为钻头面积［16］，m2；T 为扭矩［16］，N.m；RPM 为转盘转速，r/min；ROP 为机械钻速，m/min；MSE为机械比能，MPa。

2）地层物性指数模型：

地层物性指数［15］位于1 附近，1 为正常压实地层，该值小于1，机械比能基值呈现负异常，指示物性好的地层，该值越低，地层的物性越好。

3）机械比能分级（物性指数）

5.3 应用实验结果

在古城10 井、城探1 井等进行了应用，在基于距离的异常点检测算法基础上，通过机械比能基值线，计算分析得出物性指数P，根据P 值的大小来评价储层物性的好坏，物性指数越大，说明物性越差，越小说明物性越好：Ⅰ好储层：<0.4；Ⅱ较好储层0.5～0.4；Ⅲ中等储层0.63～0.5；较差储层0.7～0.63；无效储层φ＜P>0.7。储层物性［12～13］自动评价准确率在88.35%以上。

6 结语

本文所建立的异常点检测模型对储层物性的评价正确率较高，将本模型用于基于机械比能的储层的物性自动评价，在误差允许的范围内可以代替人工。且在古城10 井、城探1 井等进行了应用，储层物性自动评价准确率在88.35%以上。因此，本模型在储层物性评价方面具有良好的适用性与可行性，具有一定的工程意义和使用价值。