数学成绩和专业课成绩的相关性分析

付政庆，郭兰兰，马康楠

（1．山东科技大学数学与系统科学学院 山东 青岛 266590；（2．山东科技大学机械电子工程学院 山东 青岛 266590）

在现代社会中，数学和专业技能都被认为是非常重要的素质。大学数学课程是高校大学生极其重要的公共基础课，对大学生可持续发展能力的培养有着其他学科无法比拟的重要作用。数学成绩与专业课成绩的相关性需要深入研究。

多元统计分析是一种研究多个变量之间关系的方法，广泛应用于各个领域的数据分析。现代教学管理中也会产生大量的教学数据，大数据的分析与学习可以用来对学生行为进行早期干预，辅助教师开展教学[1]。如李静、宁勤等应用因子分析对学生成绩进行综合评价并与平均成绩法对比分析[2-3]；江志冬等采用多元统计分析方法，对学生学习成绩进行分析与研究，分析了成绩在性别、班级维度上的差异[4]。Abdelhadi Abdelhakim 用多元统计的方法研究了医师的学习风格和趋势[5]。

1 研究对象和方法

本文选择某高校测控技术与仪器专业的大学生作为研究对象，收集其综合测评的专业课成绩和数学成绩作为此次数据样本进行分析和研究。同时，还需收集其他可能影响结果的因素，如是否辍学、挂科补考等。

针对收集到的数据，采用统计方法进行数据清洗、筛选和分类，对数学成绩进行学分加权处理。主要采用主成分分析、因子分析、回归分析等方法，利用SPSS 软件进行数据处理[6]。

检验数学成绩在不同专业中是否对专业课成绩有显著影响，对相关性进行深入探究，并尝试找到影响这种关系的因素，旨在为学校教育教学提供一定的依据和理论支持。

2 数据分析过程

2.1 KMO 度量标准和巴特利特检验

KMO检验系数是一种衡量数据样本的结构效度的度量标准。KMO 值越接近1，变量间的相关性越强，越适合做因子分析。巴特利特球体检验的P值<0.05 时，数据样本的结构效度非常好，进行因子分析能得到较好的结果。

将测控技术与仪器专业的数据样本通过SPSS软件分析后，由表1 测控技术与仪器的KMO 检验和巴特利特检验可知测控技术与仪器的KMO 统计量为0.875，并且P值为0.000，故该数据非常适合进行因子分析和主成分分析。

表1 测控技术与仪器的KMO 和巴特利特检验

2.2 公因子的选取

提取值表示每个变量被公因子表达的多少，一般认为，大于0.7 就说明变量被公因子很好地表达。

由表2 测控技术与仪器的公因子方差可以看出计算机数字控制技术、信号与系统、电路基础、精密机械设计基础、自动控制原理、制图基础（A）、中国近现代史纲要、思想道德修养与法律基础、模拟电子技术、工程光学基础、误差与数据处理、毛泽东思想和中国特色社会主义理论体系概论、传感器与检测技术、大学英语（A）（2—2）、大学英语（A）（2—1）变量能被公因子很好地表达。由表3 测控技术与仪器的总方差解释可知基于特征值大于1，提取4 个因子后，4 个因子共同解释了原有变量的71.503%。

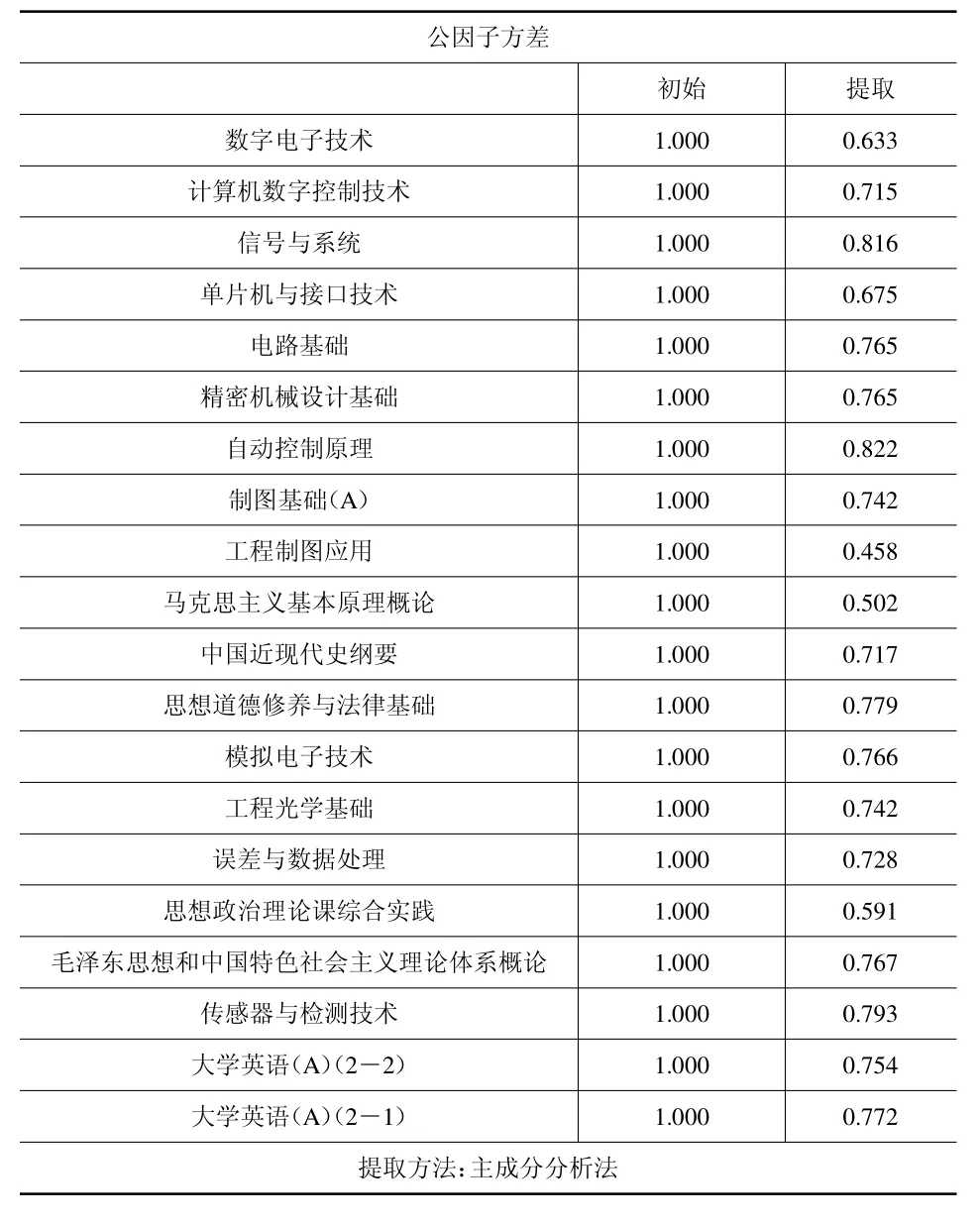
表2 测控技术与仪器的公因子方差

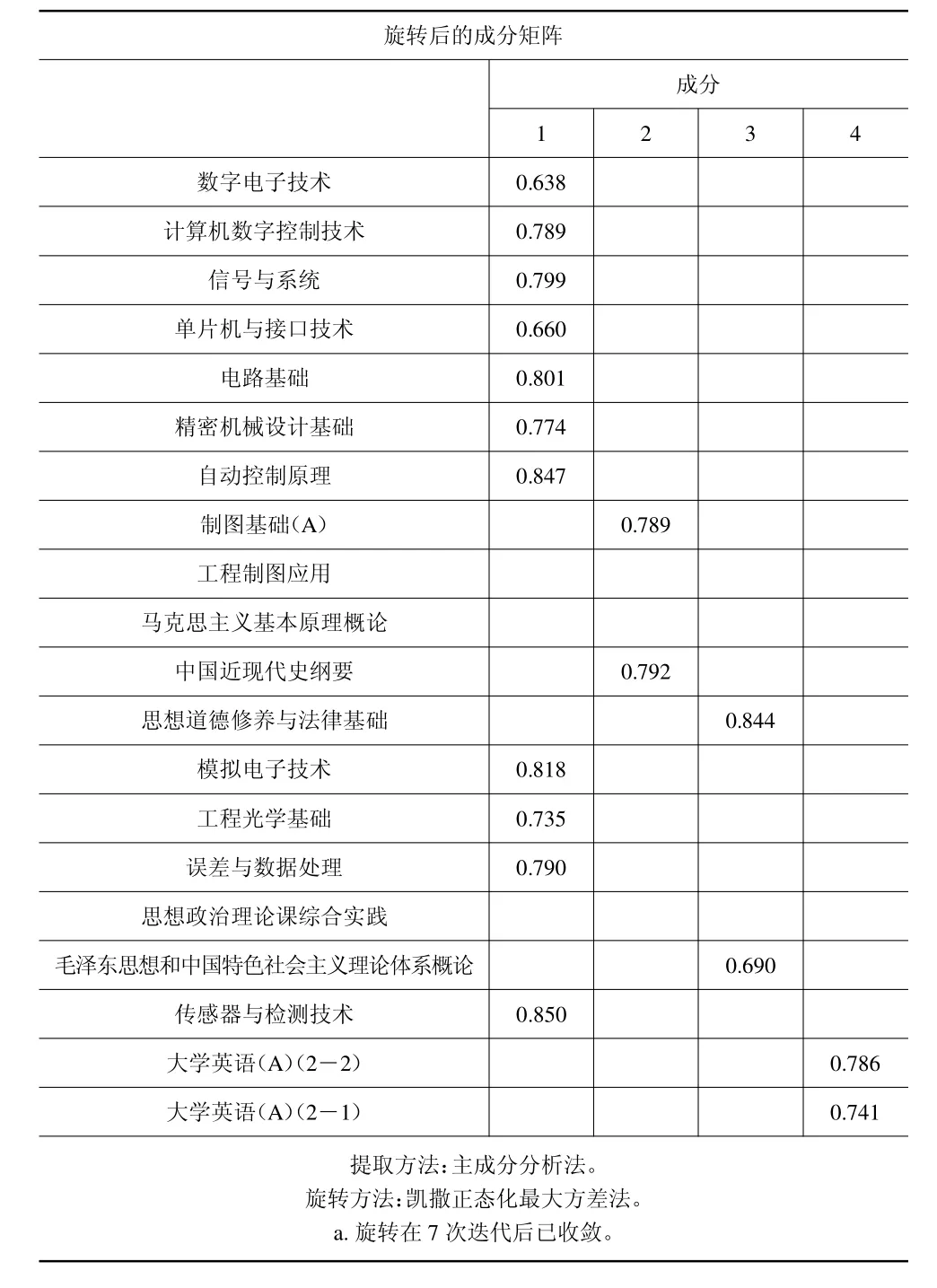
表3 测控技术与仪器的旋转后的成分矩阵

2.3 公因子解释

由表3 旋转后的成分矩阵可知，数字电子技术、计算机数字控制技术、信号与系统、单片机与接口技术、电路基础、精密机械设计基础、自动控制原理，位于第一个因子上有较高的载荷，第一个因子主要解释这几个数据，我们称之为核心课；制图基础（A）、中国近代史纲要位于第二个因子上有较高的载荷，第二个因子主要解释这几个数据，我们称之为基础课；思想道德修养与法律基础、毛泽东思想和中国特色社会主义理论体系概论，位于第三个因子上有较高的载荷，第三个因子主要解释这几个数据，我们称之为思想课；大学英语(A）（2—1）、大学英语（A）（2—2），位于第四个因子上有较高的载荷，第四个因子主要解释这几个数据，我们称之为外语课。

由表4 可以得到的得分表达式为

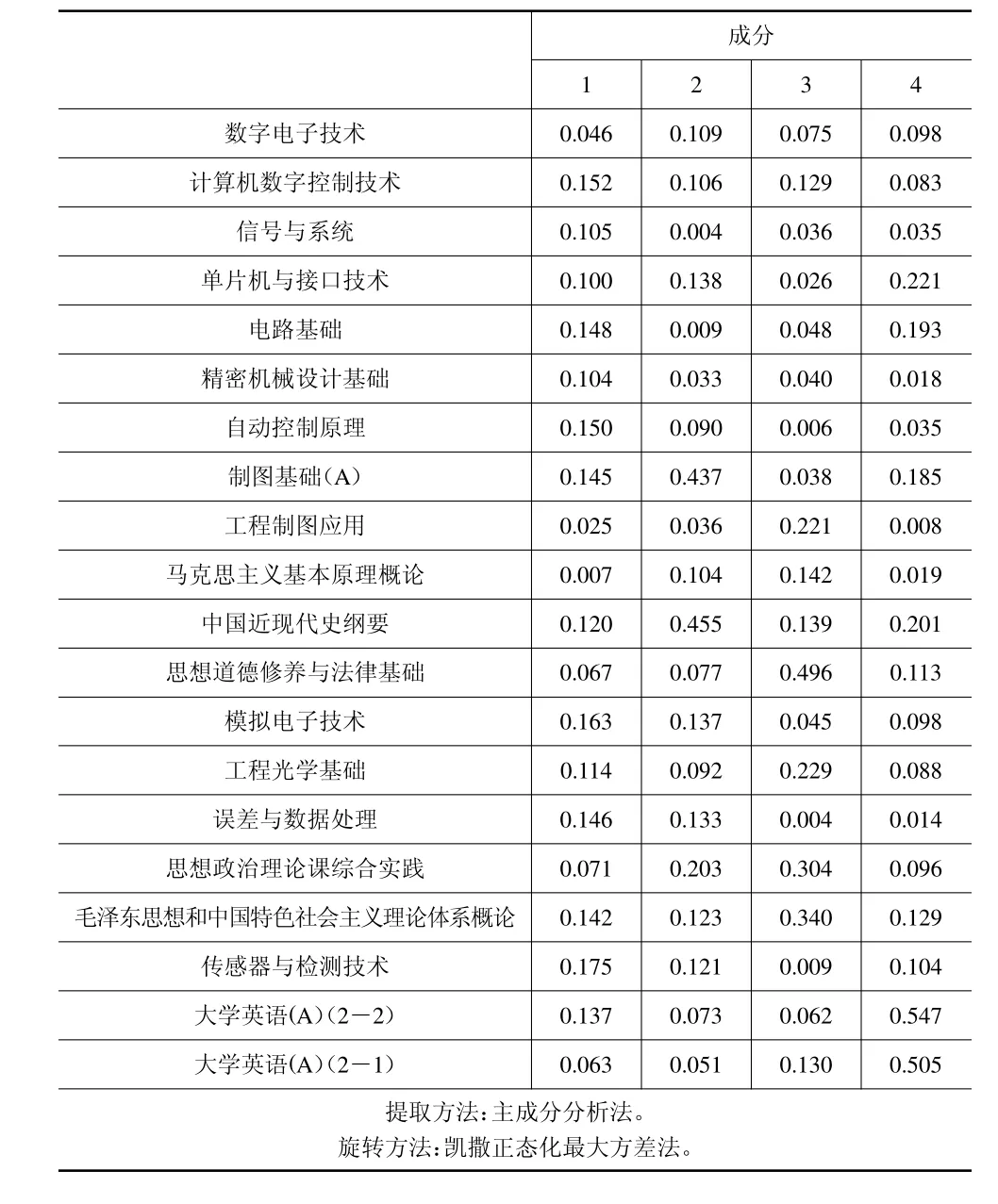
表4 测控技术与仪器的成分得分系数矩阵

式中：F1、F2、F3、F4分别是核心课、基础课、思想课、外语课。可以看出，核心课在专业课中成绩占比最大，外语课在该专业只开设了两个学期只需浅学，所以在专业课中成绩占比最小。我们通过F来得到专业课成绩。然后我们用经过主成分分析和因子分析之后得到的测控技术与仪器专业的专业课成绩做出线性回归分析图。

由图1 可以看出，测控技术与仪器专业的数学成绩与专业课成绩具有较强的线性相关性，线性关系是正向的，测控技术与仪器的数学成绩随着专业课成绩的增加而增加，专业课成绩和数学成绩的关系为1∶9.33。

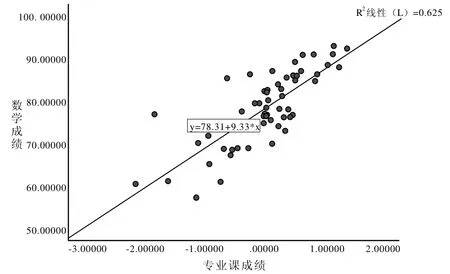
图1 测控技术与仪器的线性回归图

3 结语

本文通过对专业成绩和数学成绩之间的相关性展开了探讨和研究，利用主成分分析、因子分析和回归分析对所得结果进行分析，测控技术与仪器专业的数学成绩与专业课成绩具有较强的线性相关性，线性关系是正向的，测控技术与仪器的数学成绩随着专业课成绩的增加而增加，专业课成绩和数学成绩的关系为1∶9.33。专业课成绩与数学成绩的高低有着紧密的联系，数学成绩可以作为一个较好的参考因素，帮助评估不同专业背景下学生的表现。