油管抗内压强度及爆破失效机理研究

单 涵 ， 王 成 ， 许雷明 ， 高连新 ,*

（1. 华东理工大学 机械与动力工程学院，上海 200237；2. 江苏常宝普莱森钢管有限公司，江苏 常州 213200）

0 引言

油管是石油和天然气开采过程中的油气通道。整个油管柱就像一个圆筒形的高压容器，需要承受几十甚至上百兆帕的内压，一旦发生爆破，就会造成重大的经济损失[1-2]。因此，预测油管的抗内压强度一直是油管研究的热点。

目前的研究文献多是基于内压圆筒理论，利用弹塑性公式研究油管爆破压力的计算方法[3-4]。孙永兴等[5]在API 5C3[6]的基础上提出了油套、套管抗内压爆裂计算模型，并通过实物试验验证了该模型的精度。梁瑞等[7]研究了材料的屈强比对油套管爆裂强度的影响规律，提出了具有更高精度的油套管抗内压爆裂计算模型。周科等[8]依据弹塑性力学厚壁圆筒理论，研究了内外压共同作用下的压裂油管应力状态，提出了内外压共同作用下的压裂油管抗内压强度校核新模型。以上解析法均是对油套管的服役工况以及几何形状进行简化后得出的力学模型，因此存在一定误差。全尺寸试验法以及有限元分析法相较于解析法可以得出更具有指导意义的结果。由于爆破试验对设备要求高、试验费用贵、试验周期长，相关的研究较少。

本研究将全尺寸试验与有限元分析相结合，以油管为对象，通过水压爆破试验得到最终爆破压力值，通过应变测试的方法研究油管在爆破过程中的变形，从而深入了解油管爆破失效的过程及失效机理。同时，建立油管爆破失效分析的有限元模型，并利用试验结果对模型进行检验和修正，最后用修正的模型研究壁厚不均度、椭圆度对油管抗内压强度的影响。

1 应变测试及结果分析

取长度为1 m、规格为φ88.9 mm×6.45 mm的油管，利用水压爆破机对其进行爆破试验。爆破试验设备见图1。

图1 试验设备Fig.1 Test equipment

分别在距管端250（位置1）、500（位置2）、350（位置3）mm处粘贴应变片（图2a）。在上述位置中，沿着外壁每间隔120°粘贴一片应变片（含轴向和环向2个方向），共计粘贴9片应变片，用来测量对应位置的环向和轴向应变（图2b）。试验前对油管的外径和壁厚进行测量，结果见表1。

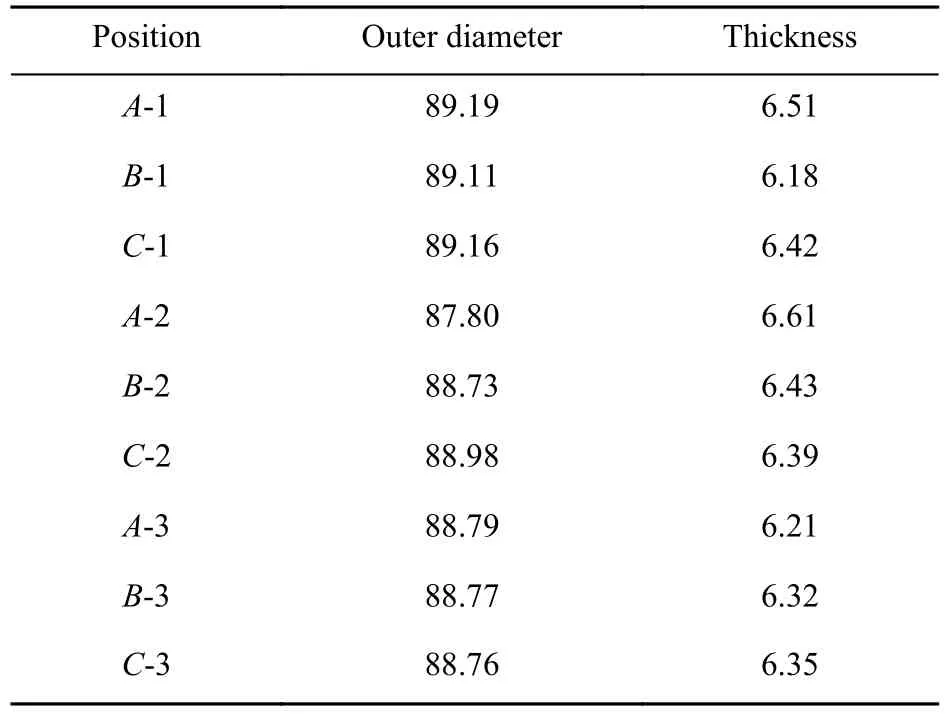
表1 外径和壁厚测量结果Table 1 Measurement results of the outer diameter and wall thickness mm

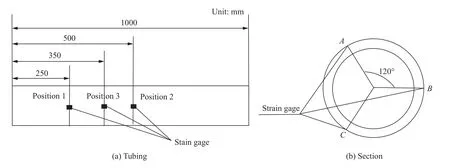
图2 应变测试位置示意图Fig.2 Schematic diagram of the position of strain test

试验前测量油管材料的力学性能，其屈服强度σs=792 MPa，抗拉强度σb=924 MPa，断口伸长率δ=15%，其拉伸曲线如图3所示。

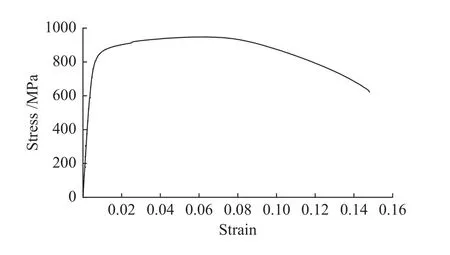
图3 拉伸曲线Fig.3 Stretch curve

用堵头封堵管子两端，以清水作为加压介质，对油管逐渐施加内压，加压到额定压力99.4 MPa后保压10 min，然后继续加压至油管爆破。最终测得油管的爆破压力为133 MPa。其加压曲线见图4。

图4 加压曲线Fig.4 Load curve

在油管位置1处测得A、B、C处的环向应变和轴向应变随内压的变化曲线如图5a所示。油管位置2、3的C处因应变片失效不做分析。位置3测得A、B处的环向应变和轴向应变随内压的变化曲线如图5b所示。由结果可见，在位置1的截面中，B处会率先发生失效，而在位置3的截面中，A处会率先发生失效，且该2处分别对应油管截面壁厚最薄点。因此，油管爆破失效首先从壁厚最薄弱的位置开始。由内压-应变曲线可见，在油管爆破过程中，各个位置的环向应变均远远大于其轴向应变，环向应变最大可达0.05，而最大轴向应变不超过0.0013。应变过大是造成油管失效的主要因素之一，而其中应重点研究环向应变的影响。

图5 油管内压-应变曲线Fig.5 Internal pressure-strain curve

2 油管抗内压强度的理论计算

2.1 API5C3抗内压屈服设计

API 5C3[6]推荐的油、套管的抗内压强度公式为：

式中：D为油、套管名义外直径，σs为油、套管屈服强度，kwall为管壁公差因子（如当公差为-12.5%时，kwall=0.875）；P1为油、套管发生屈服时的内压；t为管壁厚。

将实测平均壁厚t=6.423 mm，平均外径D=88.828 mm，最小屈服强度σs=792 MPa，kwall=0.875代入式（1）中，可得P1=96.2 MPa。

式（1）中没有考虑断裂韧性和断裂失效问题，且该计算公式是基于薄壁筒理论，未考虑大多数实际材料的硬化阶段，因此不能全面反映油管的制造技术和真实抗内压强度[9]。当D/t＞20时才视为薄壁圆筒，本规格油管不符合此条件，分析时仍视为薄壁圆筒会产生较大误差。

使用厚壁圆筒理论计算油管所受的抗内压强度已得到广泛应用[10-11]。考虑到实际工况，油管会受到内外压的共同作用，其受力符合弹塑性力学中厚壁圆筒受均布作用力。按照厚壁圆筒考虑，可以参照式（2）来计算。

式中：σs为材料的屈服强度；K为径比，即D0/Di（D0为油管外径，Di为油管内径）。将上述实测数据代入式（2），可得P2=122.7 MPa。

2.2 全管壁屈服爆裂

API 5CT[12]中提出管体初始屈服内压公式，该标准将管体视为薄壁圆筒，取整个管体发生塑性屈服为临界条件。然而油管是从内部开始屈服，随着内压增大，塑性区不断从管内壁扩展到管外壁，直至整个管壁进入塑性状态[13]。油、套管韧性爆裂失效需要一个基于全塑性极限状态模型，随着内压的增加，屈服会先在油管管体内壁发生[14]。孙永兴等[5]根据Von Mises准则，给出两端堵口的油、套管爆裂公式：

式中：D为油、套管名义外直径，σs为油、套管屈服强度，t为管壁厚，P3为全管壁屈服爆裂强度。将实测数据代入式（3）中，可得P3=142.8 MPa。

2.3 福贝尔（Faupel）公式

著名的Faupel公式也可以简便地估算压力容器的爆破压力，该公式是Faupel从若干试验总结出来的经验公式[15]：

式中：σs为材料的屈服强度，σb为材料的抗拉强度，K为径比。将上述实测数据σs=792 MPa，σb=924 MPa，K=88.828/75.982=1.169代入式（4），可得P4=163.2 MPa。

2.4 理论计算结果对比

4种爆破压力P的理论计算结果与实测内压爆破强度P0的对比见表2。

表2 理论计算结果对比表Table 2 Comparison of theoretical calculation results

由于API 5C3抗内压屈服设计是基于薄壁筒的理论设计，且未考虑断裂韧性和断裂失效问题，因此该强度P1与实测内压爆破强度P0相差较大。由于试验样管不满足薄壁圆筒，因此参照厚壁圆筒计算出来的内压爆破强度P2与实测内压爆破强度P0更加接近。塑性流动最初发生在厚壁油管内壁，且被周围的弹性材料所约束[16]。由于内壁屈服在实际试验和油田应用中都无法体现，刚开始不会丧失压力完整性，而爆裂能够真实体现油管丧失密封完整性[17-18]。因此，全管壁屈服公式能够表示油管韧性爆裂的极限状态，计算结果P3与实测内压爆破强度P0也相对比较接近。Faupel公式是用来简便估算压力容器的爆破压力，因此P4与实测内压爆破强度P0相差较大。

油管的抗内压强度是爆破过程中的重要指标，也是评价油管性能的重要参数。以上4种理论方法适用于不同规格油管的抗内压强度计算，对预测油管抗内压强度具有重要的参考价值，也对油管爆破失效机理研究具有一定的指导意义。

3 油管内压失效过程的有限元模拟

3.1 材料属性

影响内压失效的是材料的力学性能。进行有限元分析时，选取实测材料性能数据，建立有限元分析的弹塑性本构模型。弹性模量E=210 GPa，泊松比μ=0.30，材料屈服强度σ0.2=792 MPa，材料抗拉强度σb=924 MPa。参照图3的拉伸曲线，将工程应力及工程应变转化为真实应力及真实应变作为有限元模型的材料力学性能数据。

3.2 模型及载荷状况

油管是具有很长纵向轴的圆柱形物体，假设横截面大小和形状沿轴线不变，作用外力与纵向轴垂直且沿长度方向不变，管体两端受到固定约束，因此可以将内压爆破过程视为平面应变问题。

选择位置1（图2）的截面尺寸为模型尺寸。该模型与X轴正方向相交的位置为截面A，截面B、C与截面A均间隔120°，外径与壁厚尺寸见表1。模型的单元类型为CFE4R，模拟时在油管内壁施加均匀内压，还需在X轴上的2个节点分别限定X、Y方向的位移约束。有限元模型见图6。

图6 有限元模型图Fig.6 Finite element model

3.3 有限元数值模拟

在有限元模型中施加随时间线性增加的内压，直至油管爆破失效。有限元模拟分析测得的爆破内压为135 MPa，与实测爆破内压十分接近。测得截面A、B、C对应外壁的环向应变、轴向应变、位移与施加载荷的关系曲线如图7所示。

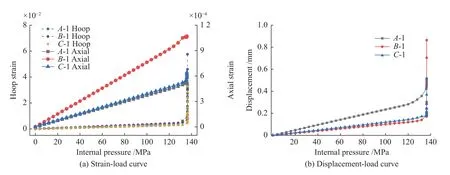
图7 应变、位移与载荷的关系曲线Fig.7 Relationship curve between strain, displacement and load

由有限元模拟结果可知：油管位置1截面A、B、C的环向、轴向应变与内压的关系曲线和实测试验结果的趋势基本一致，有限元模拟的各截面的最大应变与实测最大应变的误差在30%内。两者的对比见表3（表中的应变均为微应变）。

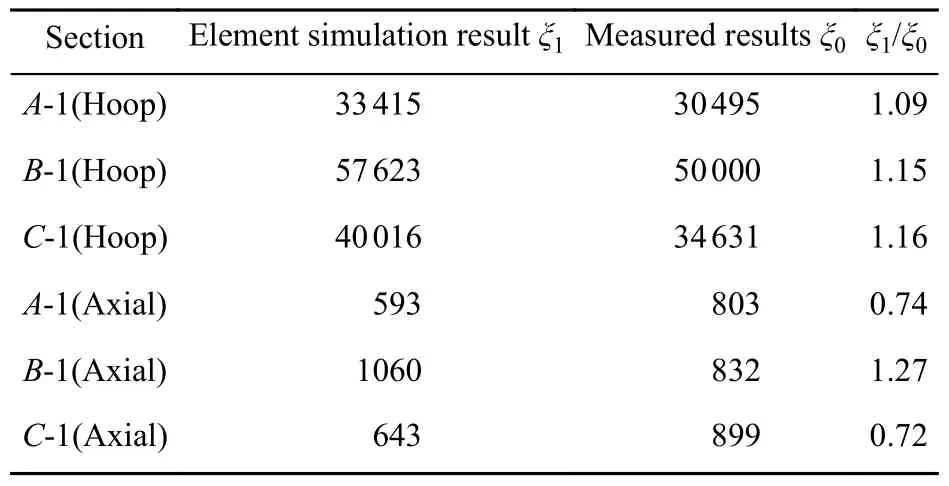
表3 有限元模拟与实测结果对比表Table 3 Comparison between finite element simulation and measured results

4 壁厚不均度和椭圆度对油管抗内压强度的影响

由于在油管的实际加工过程中存在加工误差，任意位置的外径和壁厚无法保证完全一致，因此油管的壁厚不均度和椭圆度可能是影响油管抗内压强度的2个因素。以规格为φ88.9 mm×6.45 mm的油管为例，借助有限元分析软件来分别研究这2个因素对其抗内压强度的影响。

4.1 壁厚不均度的影响

对不同壁厚的8个油管截面模型进行有限元分析，模型的外径、最小壁厚及最大壁厚等尺寸见表4。

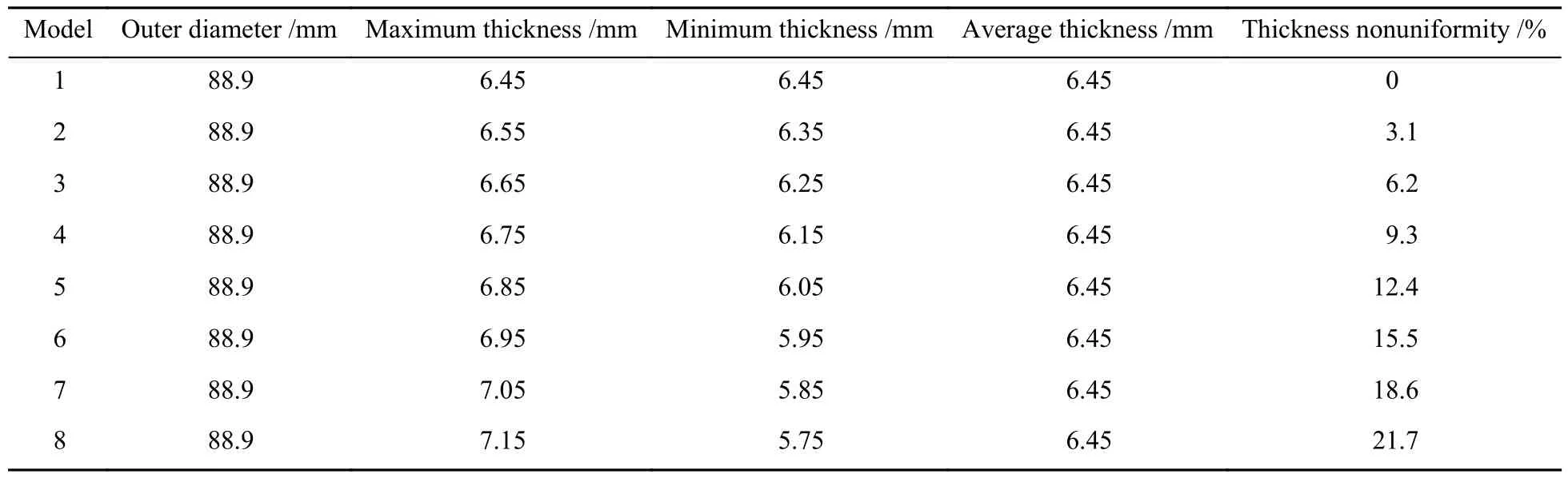
表4 壁厚不均的油管模型尺寸Table 4 Size of oil pipe models with different thickness

其中，模型1是理想圆形；模型2～8的外壁和内孔是理想圆形，但存在偏心现象，模型示意图见图8。

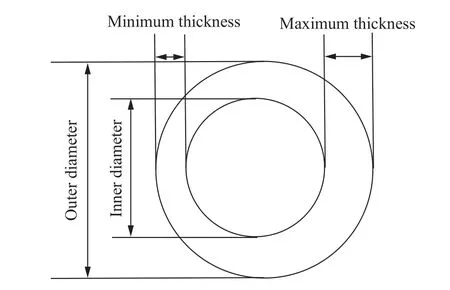
图8 偏心模型示意图Fig.8 Schematic diagram of eccentric model

取油管的某一截面为研究对象，将油管爆破问题简化为平面应变问题，模拟时在油管内壁施加均匀内压，载荷施加与位移约束参照图6。对表4中的8个模型进行有限元分析，测得抗内压强度如图9所示。由结果可知，模型1的抗内压强度为141.6 MPa；随着壁厚不均度的增加，油管抗内压强度呈明显下降趋势。模型8的壁厚不均度为21.7%，其抗内压强度为127.5 MPa，比模型1的强度降低10%。因此，壁厚不均度是影响油管抗内压强度的因素之一，且影响效果显著。

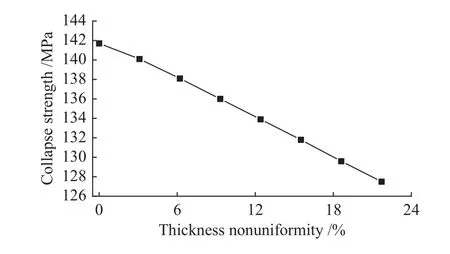
图9 壁厚不均度-抗内压强度关系曲线Fig.9 Thickness nonuniformity-collapse strength curve

4.2 椭圆度的影响

对椭圆度不同的8个油管截面模型进行有限元分析，椭圆长轴、短轴以及壁厚等尺寸见表5。

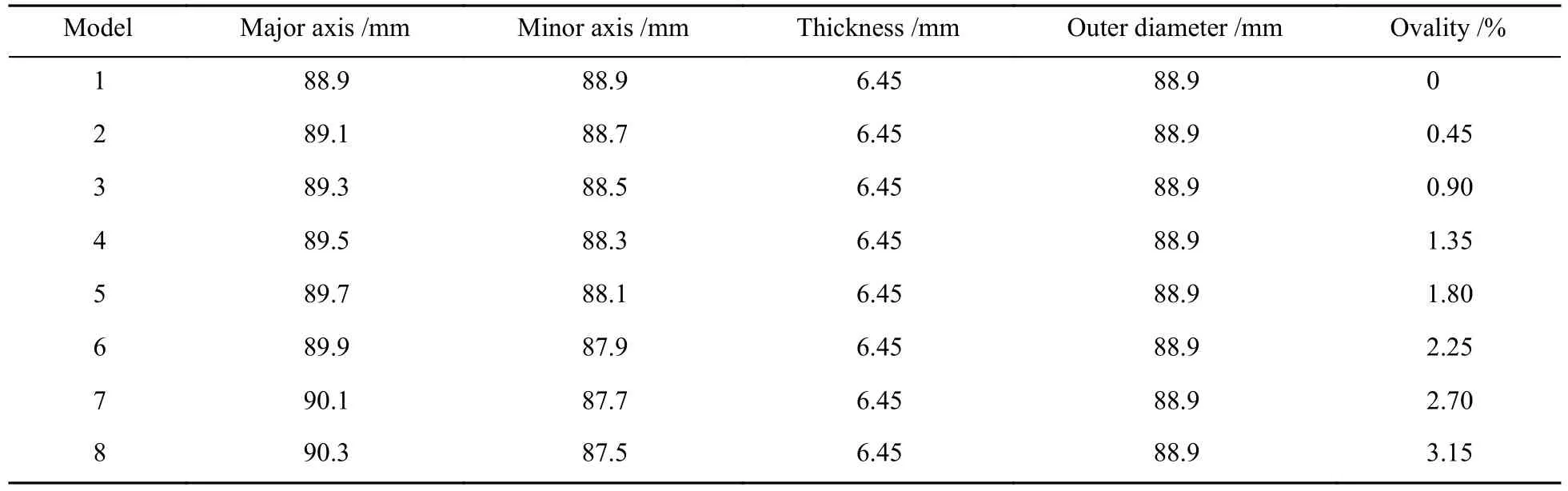
表5 不同椭圆度油管模型尺寸Table 5 Size of oil pipe models with different ovality

其中，模型1的外壁和内孔均为理想圆形；模型2～8的外壁和内孔均为椭圆形，等壁厚且不存在偏心现象，模型示意图见图10。

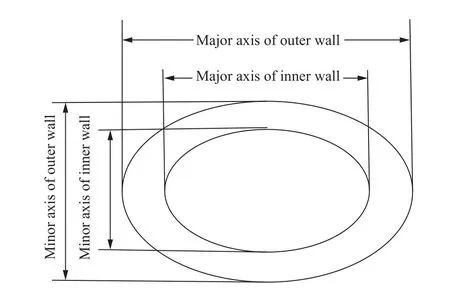
图10 椭圆模型示意图Fig.10 Schematic diagram of elliptical model

以模型2为例。在建立模型时，椭圆长轴为89.1 mm，并设置在X轴上；短轴为88.7 mm，并设置在Y轴上。各处的壁厚均为6.45 mm，同时以实测屈服强度、抗拉强度为模型材料参数。模拟时在油管内壁施加均匀内压，载荷施加与位移约束参照图6。对表5中的8个模型进行有限元分析，测得的抗内压强度如图11所示。由结果可知，随着椭圆度的增加，模型的抗内压强度呈缓慢下降趋势。模型8的椭圆度为3.15%，其抗内压强度为141.54 MPa，比模型1的抗内压强度降低0.09%。由此可知，椭圆度会影响油管抗内压强度，但效果并不显著。相对于壁厚不均度对油管抗内压强度的影响，椭圆度的影响可以忽略不计。因此，壁厚不均度是影响油管抗内压强度的主要因素之一。

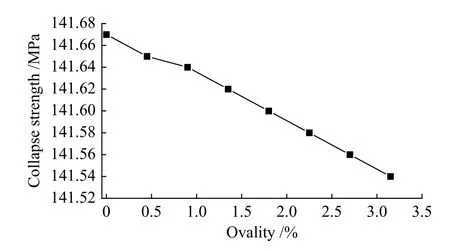
图11 椭圆度-抗内压强度关系曲线Fig.11 Ovality-collapse strength curve

5 结论

1）运用弹塑性力学理论建立的有限元模型可以较准确地预测油管的爆破失效压力，应变分布与实测值也非常吻合。

2）油管爆破过程中，加压初期外壁的应变值随内压增大而线性增加，其中壁厚较薄处的环向应变变化最显著；当达到屈服时，应变值在壁厚较薄处急剧增加，从而造成油管破裂失效。

3）壁厚不均度和椭圆度是影响油管抗内压强度的2个重要因素，其中壁厚不均度的影响更为显著。