ZM6镁合金铸件夹杂物表征及其对拉伸力学性能的影响

沈佳萌 ， 魏振伟 ， 李志农 ， 赵 伟 ， 任尚坤 ， 刘昌奎 ， 杨光山

（1. 无损检测技术教育部重点实验室（南昌航空大学），南昌 330063；2. 中国航发北京航空材料研究院，北京 100095；3. 中国航发哈尔滨东安发动机有限公司，哈尔滨 150066）

0 引言

镁是地球上储量最丰富的轻金属之一。ZM6镁合金具有密度低、强度高、易于铸造和加工等优异性能，被广泛应用于轻质构件，近年来在航空、航天、汽车和电子工业等领域中得到应用，并得到快速发展[1-4]。但ZM6镁合金在铸造过程中不可避免地会产生缺陷，如夹杂、孔洞、疏松和偏析等[5]。尤其是Mg易与氧反应生成氧化物夹杂，夹杂物的存在破坏了基体的连续性，造成局部应力集中，严重影响ZM6铸件服役性能，大大降低了ZM6镁合金使用的可靠性和安全性。

国内外学者对材料夹杂物缺陷一直在进行深入的研究。SOUAMI N等[6]研究了含 12%Cr的不锈钢中夹杂物对于韧性断裂的影响，发现夹杂物是裂纹萌生和扩展的起点，夹杂物是诱发不锈钢发生断裂的重要因素。周建川等[7]通过研究夹杂物对高强钢性能的影响，发现夹杂物的存在破坏了基体组织的连续性，促进裂纹的萌生。陶延夏等[8]采用有限元方法建立了含有球状夹杂物的有限元模型，研究在挤压力的作用下夹杂物对WE43镁合金的变形行为的影响。结果表明，夹杂物在挤压力的作用下受压变形，在与基体接触的界面处产生较大的应力集中，使得界面脱离，成为微裂纹萌生的源头。以上研究表明，材料内部夹杂物的存在是材料发生断裂的重要因素之一。由于夹杂物与周围基体的性能差异较大，破坏了基体的均匀性和连续性，在变形过程中易产生应力集中，导致微裂纹的萌生[9]，从而降低合金性能，使其容易断裂。而夹杂物对ZM6镁合金性能的影响程度未见报道。

夹杂物的存在会对铸件材料的拉伸性能产生深远的影响，但对铸件中夹杂物的研究多为定性分析，很少对夹杂物进行定量研究和对含有不同含量夹杂物铸件的力学性能进行预测。为了进一步建立夹杂物与ZM6镁合金拉伸性能之间的关系，本研究将对ZM6镁合金中的夹杂物进行定量研究和有限元仿真分析。通过X射线筛选含有夹杂物的ZM6镁合金进行拉伸性能测试，对试样拉伸断口进行观察、统计分析，对夹杂物进行定量表征，建立夹杂物与镁合金力学性能之间的定量关系。利用ANSYS软件对含有夹杂物的镁合金进行有限元仿真分析，建立含夹杂物的ZM6镁合金单轴拉伸试验有限元仿真模拟，计算在单轴拉伸状态下夹杂物及周边基体的应力分布，进而从宏观力学的角度分析夹杂物的微观力学行为，并对不同含量夹杂的ZM6镁合金力学性能进行预测。这对于ZM6镁合金产品的设计、服役安全评估具有重要意义。

1 实验过程

1.1 实验方法

以T6态ZM6镁合金铸锭为基材进行试样制备。ZM6镁合金的化学成分见表1。按ASTM E8/E8M[10]机械加工成圆形拉伸试棒，其尺寸和形状如图1所示。将拉伸试棒进行X射线检测，挑选出工作段含有夹杂的试样。

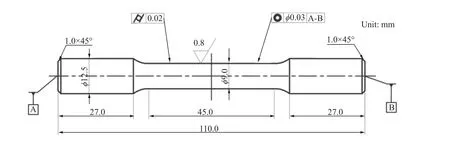
图1 圆形拉伸试样形状及加工要求Fig.1 Shape and machining requirements for circular tensile specimens

表1 ZM6合金化学成分（质量分数 /%）Table 1 Chemical composition of ZM6 alloy (mass fraction /%)

根据HB 5143—1996[11]进行拉伸试验。依次使用体视显微镜和扫描电镜（SEM）对试样断口进行宏观、微观形貌进行观察，以及使用能谱仪（EDS）对夹杂物进行成分分析。

1.2 夹杂物的表征

随着科学技术的发展和材料研究手段的进步，对铸造缺陷的表征手段和方式也多种多样。谭伟[12]采用X射线计算机断层扫描技术（Computed Tomography，CT），在不损伤试样的前提下对铸造缺陷进行三维重构，进而测量缺陷的三维尺寸；何承群等[13]使用夹杂物最大的投影面积S（S=长轴×短轴）将夹杂物三维尺寸转换为二维尺寸对夹杂物进行表征。

由于夹杂物形状的复杂性、分布的不确定性，很难在三维空间上对夹杂物尺寸进行测量，且本研究需要进行大量拉伸实验，因此，为对夹杂物进行快捷和准确地定量表征，本研究将对拉伸断口处的夹杂物实际面积进行测量。使用体视显微镜对试样断口进行拍照，如图2所示，测量出断口上夹杂物的真实面积S，按式（1）计算夹杂物的等效直径d，以此对夹杂物进行表征。

图2 夹杂物面积测量Fig.2 Inclusion area measurement

2 结果与分析

2.1 拉伸断口分析

图3为拉伸试样断口的宏观形貌，可见断口上有黑色夹杂物分布在试样的表面或近表面位置。图3a中夹杂物面积为0.29 mm2；图3b中有多个夹杂，其中大夹杂物面积为6.95 mm2。夹杂物周围可见以夹杂物为中心向四周发散的扩展棱线，表明断裂从夹杂物起源并向四周扩散。夹杂物是ZM6发生断裂的重要因素，因此准确评估ZM6材料中夹杂物对其力学性能的影响十分必要。

图3 试样断口宏观形貌Fig.3 Macroscopic morphology of specimen fracture

图4 为ZM6合金试样断口的微观形貌。图4a和图4b分别为试样断口上有一个和多个夹杂物的微观形貌，可以发现，夹杂物分布在基体之中，它的存在破坏了ZM6基体的连续性，其周围存在撕裂棱向外扩展的现象。对夹杂物进行能谱分析，图4a中夹杂物的O、Mg元素含量分别为70%、30%（质量分数，下同），图4b中夹杂物的O、Mg元素含量分别为51.7%、48.3%。由此可知，ZM6铸件中的夹杂物为MgO。

图4 试样断口微观形貌Fig.4 Fracture morphology of sample

2.2 夹杂物对拉伸力学性能的影响

ZM6镁合金的抗拉强度和伸长率随着夹杂物等效直径的增大而降低（图5）。本研究采用一元线性回归法对夹杂物尺寸和ZM6合金抗拉强度进行定量研究，得到抗拉强度σb与等效直径d的拟合公式为：

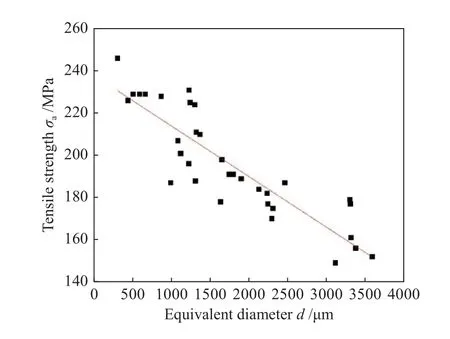
图5 抗拉强度与等效直径的关系Fig.5 Relationship between tensile strength and equivalent diameter

ZM6镁合金伸长率δ和等效直径d的关系如图6a所示，δ与d呈幂函数关系分布。转换为Lnd、Lnδ形式后的关系如图6b所示，此时呈线性分布。采用一元线性回归法对其进行线性拟合，得到拟合公式为：

表2为抗拉强度和伸长率的回归相关系数R和标准差R2。一般来说，R为0.5～0.8，为显著相关；R大于0.8为高度相关[14]。式（2）、式（3）的R分别为0.88、0.83，表明抗拉强度和伸长率与等效直径的相关性较好。因此，式（2）、式（3）能较好地反映抗拉强度及伸长率与夹杂物尺寸（等效直径d）之间的相关性。

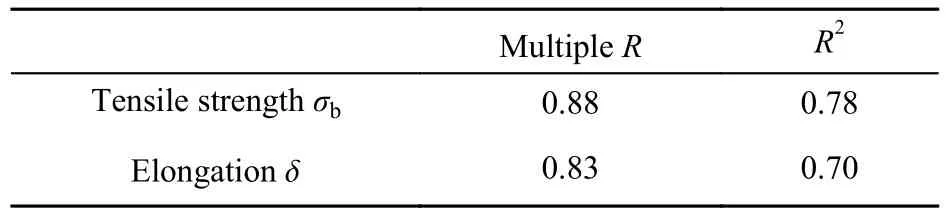
表2 回归相关系数Table 2 Coefficient of regression correlation

2.3 有限元仿真

试样断口中的夹杂物形状各异，本研究以圆球代表夹杂物，以等效直径d表示夹杂物大小。采用ANSYS软件进行有限元分析，建立不同等效直径的夹杂物，研究夹杂物尺寸对ZM6拉伸性能的影响。

对无缺陷的ZM6镁合金试棒进行拉伸试验，测量出其弹性模量E=43.84 GPa，抗拉强度σb=207 MPa。对于ZM6镁合金夹杂物MgO，根据文献[15]可知，MgO的弹性模量为299 GPa，泊松比μ=0.18。

建立圆棒拉伸试样的三维有限元实体，将圆形夹杂物放置于试棒的中间部位且靠近试棒表面。采用四面体网格，单元类型为Solid186进行网格划分；将试样一端固定，另一端施加载荷进行边界条件设定（图7a）。圆形试棒拉伸有限元分析Miss应力云图如图7b所示，对图7b中夹杂物中心的应力云图进行分析，可以发现夹杂物小球的存在使其周围的基体产生应力集中，应力最大值位于夹杂附近基体最薄位置。

图7 含夹杂缺陷ZM6圆形拉伸试样有限元分析Fig.7 Finite element analysis model of ZM6 circular tensile specimen with inclusion defects

为更好地研究夹杂物大小对ZM6合金拉伸性能的影响，通过大量的有限元仿真模拟，得到的模拟曲线与试验曲线基本一致，偏离误差在5%以内（图8）。建立d=1.0、1.5、2.0、2.5、3.0、3.5 mm等6种不同等效直径的圆球状夹杂物，采用该有限元模型进行模拟，结果见图9。由此可以发现，不同尺寸夹杂物有限元模拟得到的抗拉强度分布在拉伸试验实测最小、最大试验值之内，误差在10%以内。且随着等效直径的增大，圆形拉伸试棒有限元模拟得到的最大应力不断降低。因此，采用本研究建立的有限元模型可以准确预测不同尺寸夹杂的拉伸性能。

图8 试样的拉伸试验曲线与有限元模拟曲线Fig.8 Tensile test curve of the sample and finite element simulation curve

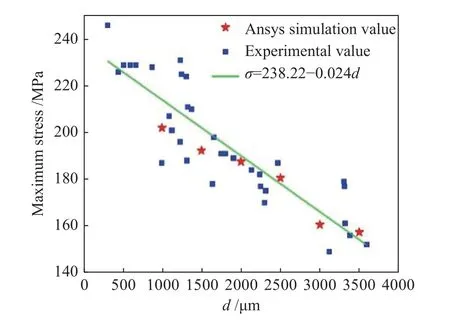
图9 不同当量直径下实验抗拉强度与Ansys模拟的最大应力Fig.9 Experimental tensile strength and the maximum stress simulated by Ansys under different equivalent diameters

3 结论

1）拉伸试样断口夹杂物成分为MgO，分布在试样的表面或近表面。夹杂物的存在破坏ZM6基体的连续性，在拉应力的作用下，断口可见从夹杂物向外扩展的撕裂棱特征。

2）采用一元线性回归法得到抗拉强度和伸长率与夹杂物等效直径之间的定量关系式分别为σb=238.22-0.024d和lnδ=-0.97lnd+7.6。随着等效直径的增大，抗拉强度和伸长率均逐渐降低，等效直径能够很好地表征夹杂物尺寸。

3）建立含夹杂缺陷的ZM6镁合金有限元模型。夹杂物的存在使合金基体和夹杂物界面位置形成应力集中，应力最大值位于夹杂物附近基体最薄位置。仿真得到的应力-应变曲线与试验曲线偏离误差在5%以内，最大应力与试验抗拉强度的误差在10%以内，建立的有限元模型能够较准确地预测含不同尺寸夹杂物ZM6合金的拉伸性能。