某空气舵系统非线性建模及参数识别

周国峰，刘 博

（中国运载火箭技术研究院，北京 100076）

引言

空气舵是广泛使用的飞行器操纵机构，通过舵面偏转产生气动控制力，实现飞行器姿态和轨迹控制的目的，是飞行控制系统中的关键部件。

空气舵系统中含有运动副，因此不可避免地存在间隙与摩擦等非线性因素。大量研究表明，间隙等非线性因素会对舵翼结构气动弹性特性产生显著的影响［1-7］。赵永辉等［1］研究了三自由度二维翼段系统中操纵面铰链间隙导致的系统极限环振动，并发现振幅、频率随着来流速度增加而跳跃的现象。杨宁等［2］分析了折叠翼结构的间隙非线性颤振，发现具有初载间隙的典型折叠翼结构也会产生稳定的极限环振荡，且结构响应与初始扰动相关。薛红军等［3］针对飞机操纵系统，建立了间隙的非线性接触模型，并采用修正的库伦摩擦模型描述间隙的摩擦作用，详细研究了含间隙机构的动态特性。王成华等［4］建立了舵系统含间隙与摩擦的单自由度数学模型，研究了舵结构系统飞行自激振动现象的产生机理。Na 等［5］研究了折叠旋转尾翼的超音速气动弹性问题，发现铰链间隙导致旋转速度增加，引起颤振速度的降低；而相同转速下，间隙非线性增强了系统气动弹性稳定性。Kholodar［6］研究了飞机控制面及挂架间隙对颤振极限环振动量级的影响，发现随着间隙的增加，座舱振动环境变恶劣，到一定程度会影响飞行员驾驶。胡海岩等［7］对国内外控制面间隙非线性研究进展进行了综述，并指出控制面铰链间隙非线性联合作用下的气动弹性控制问题是今后一个时期值得关注的问题之一。

在本文作者多年的飞行器工程研制实践中，也同样一直在分析解决间隙和摩擦非线性对舵系统传递特性的影响。如果这一问题解决不彻底就会在飞行中产生伺服弹性问题甚至气动伺服弹性问题。为了开展针对性设计，需要建立合理的舵系统的非线性动力学模型，并通过试验数据辨识确定模型中的所有参数。非线性系统辨识方法的研究从20 世纪70 年代开始，由最开始的单自由度系统到复杂的工程结构，得到大量学者的关注。提出了能量法［8］、频域法［9］、基于遗传算法［10］和等效线性化理论的各种方法［11］等。文献［12-13］将近几十年的相关方法分为7 类，进行了系统地综述，指出连接环节的间隙、摩擦等非线性因素建模与参数识别是当前结构动力学领域的焦点之一。

本文以某航天飞行器空气舵系统为研究对象，考虑运动副间隙和摩擦，采用理论与试验相结合的方法，研究建立其非线性动力学模型。

1 系统建模

1.1 系统组成

空气舵执行机构包括伺服系统和空气舵机构两个单元，一般由不同的单位按照控制系统提出的指标设计生产［14］。本文讨论的对象是舵机构机械部分，如图1 所示，包括舵面、舵轴、曲柄连杆等，后续简称空气舵系统。与其连接的边界是支撑舵轴的轴承和推动舵面转动的伺服作动器。

图1 空气舵系统Fig.1 The air rudder system

舵面通过舵轴与曲柄连接，舵轴通过轴承安装于支撑舱段上，作动器推动曲柄使舵轴带动舵面偏转，从而产生气动控制力，通过舵轴和轴承传递到飞行器上，控制飞行器姿态和轨迹。

1.2 系统动力学方程

一般航天运载飞行器空气舵展长等舵面尺寸较小，厚度较大，舵面刚度大，相当于一个刚体，因此舵轴的扭转刚度和曲柄连杆组件的刚度往往对舵面偏转过程中系统的刚度起决定性作用。

在舵系统动力学测试时，一般将舵轴的支撑轴承和作动器输出端固定，在舵面施加激励，并测量舵面转角响应，可得到如图2 所示的空气舵系统数学模型示意图。图2 中，Jr为空气舵绕舵轴的转动惯量，K为舵轴与曲柄连杆组件及作动器模拟件串联后的等效扭转刚度，C为等效黏性阻尼系数，2e为运动间隙，Tf为舵轴转动过程的摩擦力矩，Tc为气动控制力对舵轴的力矩，θr为舵面转角。虽然从严格的机构等效角度看，Jr，K和C会随着舵面转角的变化而变化，但是变化量非常小，工程上可近似认定其为常数。

图2 空气舵系统数学模型示意图Fig.2 Mathematical schematic of the air rudder system

根据图2，空气舵的动力学方程为：

式中Tk为考虑间隙的弹性恢复力矩，其表达式为：

从已有研究结果看，摩擦力矩Tf一般采用Coulomb 摩擦模型和Stribeck 摩擦模型获得。如果采用Coulomb 摩擦模型，则：

式中Mf为Coulomb 摩擦力矩。

如果采用Stribeck 摩擦模型，则：

式中Mf为静摩擦力矩；k1，k3为动摩擦力矩曲线方程系数，具体形式如下：

式中vm为动摩擦力矩最小时的舵面角速度；k0为最小动摩擦力矩与静摩擦力矩Mf之比，当k0=1时，Stribeck 摩擦模型退化为Coulomb 摩擦模型。

显然，无论采用哪种摩擦模型，这都是一个非线性系统，其传递函数不能简单地表示成线性有理分式的形式，通过识别分子分母多项式系数的形式完成传递函数参数的确定。因此，需要识别式（1）中所有的物理参数。工程实际中，一般空气舵转动惯量Jr是可以测量的，式（1）中独立的未知参数有4 个（即采用Coulomb 摩擦模型时的K，C，Mf，e）或6 个（即采用Stribeck 摩擦模型时的K，C，Mf，e，k0，vm），因此是一个四参数或六参数模型。

1.3 幅频响应求解

文献［10-11］中提出过各种参数识别方法，由于在工程中测量系统的频响是非常成熟和方便的，因此本文将讨论基于频响测试的舵系统非线性参数识别方法。与文献［11］的常位移测试和常速度测试不同，本文采用的是传统的常力测试。

参考图2，频响测量时，由激振力取代气动控制力测量舵面的响应。为了识别系统参数，需要首先得到频响函数表达式。

采用谐波平衡法对式（1）进行求解。由于飞控系统设计关注频段只包含主共振，因此，可以忽略高次谐波，仅保留一次谐波项。设在如下正弦激励下：

舵面响应为：

式中T0和θ0分别为激励力矩和舵面转角的幅值；ω为激励频率；h为响应与激励的相位差。

1.3.1 四参数模型

四参数模型采用Coulomb 摩擦模型。将式（2），（3），（6）和（7）代入式（1）后取出一次谐波项的系数，得到两个谐波平衡方程：

式中φ=arcsin(e/θ0)。

通过式（8）和（9）消去相位差，得到舵系统四参数模型幅频函数方程：

由于φ=arcsin(e/θ0)，所以式（10）是一个超越方程，无法求得幅频函数的精确显式解析表达式。

观察式（10），如果令：

为含间隙影响的等效刚度，则可由式（10）求得如下幅频响应函数：

由式（12）可知，与线性单自由度系统类似，幅频函数在ω=附近达到极值。

1.3.2 六参数模型

六参数模型采用Stribeck 摩擦模型。将式（2），（4），（6）和（7）代入式（1）后取出一次谐波项的系数，得到两个谐波平衡方程：

通过式（13）和（14）消去相位差，得到舵系统六参数模型幅频函数方程：

2 试验及舵系统参数识别

2.1 试验情况

对该飞行器实际使用的空气舵系统开展频响测量试验，如图3 所示。激振点设置在空气舵根弦的最前端，以获取较大的扭矩。通过根弦上的两个加速度传感器获取舵面转角响应。

图3 空气舵系统频响试验Fig.3 FRF test setup of the rudder system

测试时，激振器向舵面施加幅值为常数的正弦扫描激励，激振力矩与激振力关系按下式计算：

式中l为激振点到舵轴中心的距离。

同时采集加速度传感器输出，并由下式计算得到舵面转角加速度，通过频域分析获得频响曲线：

式中A1和A2为加速度传感器测量值；L为两个加速度传感器间的距离。

试验测量了等效扭转力矩幅值分别为70 N·m（A 组）和60 N·m（B 组）的两组数据，结果如图4 所示。图4 中λ为采用控制系统关注频带上限频率归一化后的无量纲频率比。频率归一化对应的转动惯量Jr=63062.8 N ⋅m。

图4 某飞行器空气舵系统频响试验数据Fig.4 FRF test data of the rudder system of a launch vehicle

由图4 可见，随着激振力矩幅值的增加，主共振频率和共振峰峰值都有明显提高，这是典型的非线性系统动力学特征。

2.2 参数识别

工程实际中，频响测试的激振力矩幅值T0(ω)和响应幅值θ0(ω)是可测得的。根据式（10）和（15）隐函数形式幅频函数，采用MATLAB 非线性最小二乘工具nlinfit 函数拟合试验数据即可完成物理参数的识别。该工具函数使用高斯-牛顿算法，计算时间短、效率高，但比较依赖初值的选取。因此，可以用两组频响测试峰值点处的频率ω0，力矩幅值T0(ω0)，响应幅值θ0(ω0)等信息，根据式（12）对K，C，Mf，e的值进行初步估计，作为使用nlinfit 函数的初值。

分别对A 组、B 组和（A+B）组测试数据进行拟合，结果如表1 和2，图5 和6 所示。其中，（A+B）组识别工况是指将A 组和B 组测试数据联合起来作为nlinfit 函数的输入数据进行参数辨识，用以考察是否存在一个拟合结果可以同时兼顾A 组和B 组测试数据。

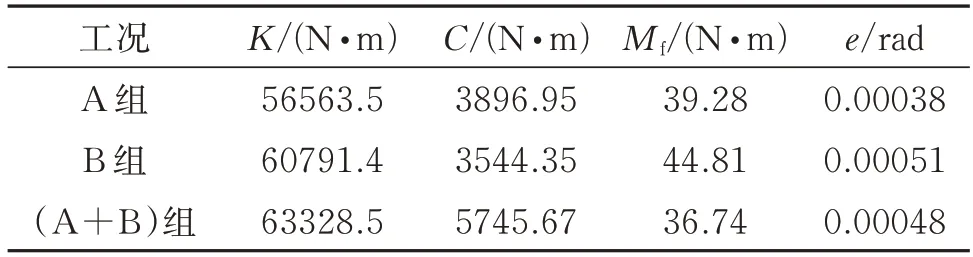
表1 四参数模型识别结果（频率归一化后）Tab.1 Identified values with the four-parameter model（with frequency normalization）

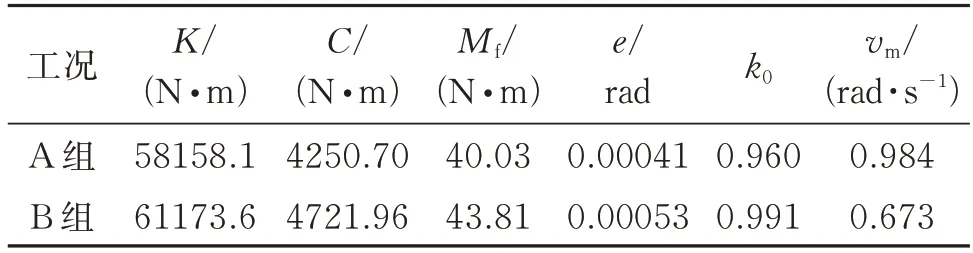
表2 六参数模型识别结果（频率归一化后）Tab.2 Identified values with the six-parameter model（with frequency normalization）

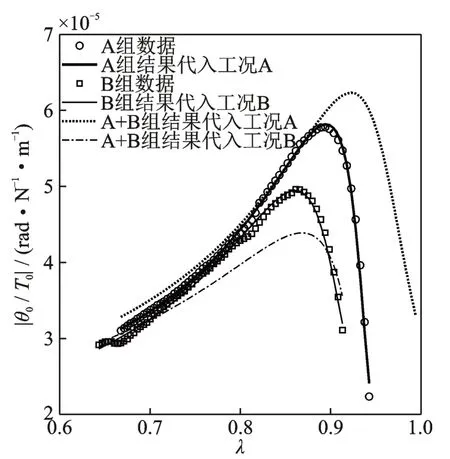
图5 四参数模型拟合结果Fig.5 Curve fittings of the test data with the four-parameter model

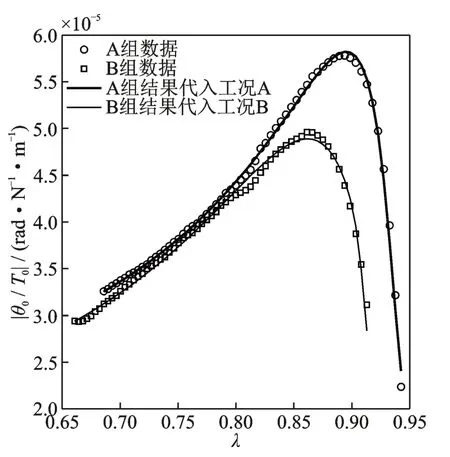
图6 六参数模型拟合结果Fig.6 Curve fittings of the test data with the six-parameter model

从识别结果可见：

（1）无论采用四参数模型（Coulomb 摩擦模型）还是六参数模型（Stribeck 摩擦模型），采用单一工况数据时，都可以较好地拟合试验数据，但是识别的Stribeck 摩擦模型参数k0接近1，基本退化至Coulomb 摩擦模型。

（2）单独采用A 组或B 组测试数据进行拟合时，拟合结果和试验结果均吻合较好，但是两组数据识别的结果有一定差异。出现此现象有两种可能：一是模型不可靠，将每种工况识别的参数代入模型只是对真实舵系统在该工况的一种近似“等效”；二是这个非线性拟合问题的解不唯一，两组数据识别得到的两组模型参数结果至少有一组是“虚假”的。如果是后者，那么同时采用两组测试数据，即（A+B）组工况，识别的模型参数结果应也适用于A 组和B组试验数据。然而，从图5 看，情况恰恰相反，（A+B）组识别结果并不能分别很好地拟合A 组和B 组数据。

综上可知，四参数模型和六参数模型都只能在单一激励工况近似“等效”地描述实际系统幅频传递特性，由一个工况测试结果识别出的系统参数并不能用来预示其余工况的动力学特性。因此，这两个模型都不够可靠。

3 五参数模型及识别结果

第1 节和第2 节所讨论的两个模型由于可靠性不足，无法用于飞控系统的设计与分析。本节将对其进行改进，提高模型可靠性。考虑到对于该空气舵，Stribeck 摩擦模型相对于Coulomb 摩擦模型并无明显优势，因此在原四参数Coulomb 摩擦模型基础上进行改进。

参考图3，当激振器激励舵面时，对舵轴除了产生扭矩Tc(t)，还对舵轴支撑轴承运动副有一个正压力F(t)。那么根据接触面Coulomb 摩擦的产生机理，由这个随时间变化的激振力产生的摩擦力矩大小也与其成正比，即与Tc(t)成正比。因此，可在式（3）基础上，将摩擦力矩Tf进行细化，描述如下：

式中Mf为摩擦力矩的常值项；|μ⋅Tc(t)|为比例项，引入的新参数μ为摩擦系数。此时，式（1）描述的系统模型中独立的未知参数有5 个（即K，C，Mf，μ，e），变成一个五参数模型。

采用谐波平衡法，忽略高次谐波，将式（2），（18），（6）和（7）代入式（1）后取出一次谐波项的系数，得到两个谐波平衡方程：

考察式（19）和（20），由于相位差h不仅在三角函数中存在，在三角函数外也存在，无法类似四参数模型通过两个谐波平衡方程消去相位差得到幅频函数方程。因此，五参数模型参数识别仅采用幅频测试数据是不够的，需要同时采用幅频和相频测试数据。

在四参数模型参数识别基础上，应用五参数模型，通过非线性拟合法分别对A 组、B 组和（A+B）组测试数据进行拟合，结果如表3 和图7 所示。

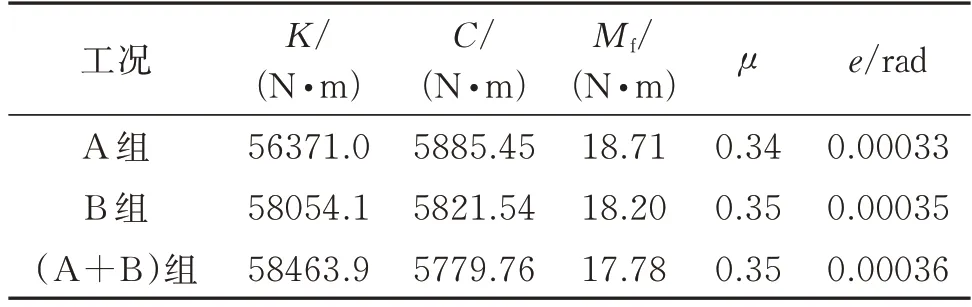
表3 五参数模型识别结果（频率归一化后）Tab.3 Identified values with the five-parameter model（with frequency normalization）

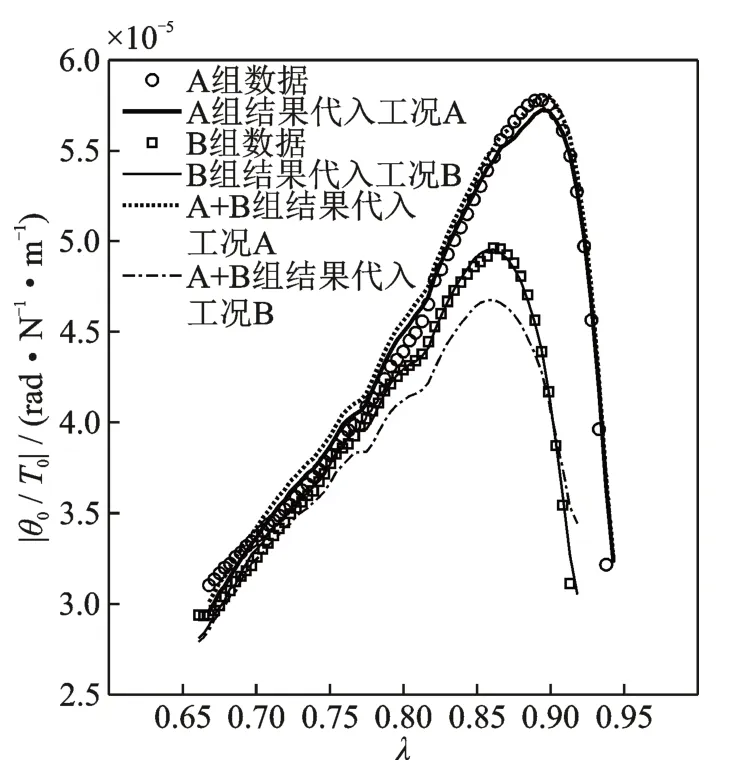
图7 五参数模型拟合结果Fig.7 Curve fittings of the test data with the five-parameter model

可见，采用不同测试数据识别获得的5 个参数一致性较好，说明五参数模型可以更可靠地描述该空气舵系统动力学特性。

五参数模型与四参数模型的差别在于摩擦模型。无论何种摩擦模型，其作用都是耗能，在幅频响应分析中可采用能量等效的原则，将其简化为线性黏性阻尼［15］。Coulomb 摩擦模型或改进摩擦模型式（18）中的常值项等效阻尼系数为：

它不是常值，反比于振动频率及振幅。

式（18）中的比例项等效阻尼系数为：

它也不是常值，反比于振动频率及振幅，正比于激振力幅值，并与相位差h相关。

根据式（21）和（22），五参数模型总的等效阻尼系数为：

四参数模型总的等效阻尼系数为：

代入表1 和3 中的参数，以及图4 中的试验数据，得到A 组和B 组工况两种模型总等效阻尼系数对比情况，如图8 所示。

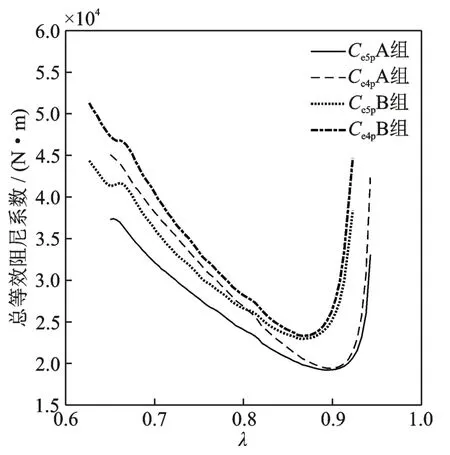
图8 两种模型总等效阻尼系数的对比Fig.8 Comparison of the total equivalent damping coefficients between the two models

单独看A 组工况或B 组工况，四参数模型识别结果得到的总等效阻尼系数大小和随频率变化特点均与五参数模型接近，特别是在共振峰附近，二者几乎一致，但四参数模型A 组和B 组工况识别的系统参数差异较大，五参数模型两个工况基本保持一致，说明四参数模型及其参数辨识结果只能在单一激励工况近似“等效”为五参数模型。

值得指出的是，火箭等飞行器在大空区域、宽速域飞行过程中，飞行动压、攻角和舵偏角均实时变化，舵面负载随之变化。摩擦系数μ的引入，可以反映舵系统摩擦力矩在飞行中的变化情况，适用性更强。

此外，对比表1，2 和3，五参数模型刚度和间隙参数的识别结果相对四参数模型较小。参考式（11），间隙正误差增加可以一定程度抵消刚度正误差，所以仅从幅频响应角度，表1，2 和3 的刚度和间隙参数都是满足拟合要求的。但是五参数模型参数识别中使用了相频信息，因此表3 的识别结果更可靠。

4 结论

本文以某航天飞行器空气舵系统为对象，考虑运动副间隙和摩擦，采用理论与试验相结合的方法，研究了系统非线性动力学建模问题，提出一种基于改进Coulomb 摩擦模型的五参数模型。相比于基于Coulomb 摩擦模型的四参数模型和基于Stribeck 摩擦模型的六参数模型，五参数动力学模型拟合不同工况测试数据获得的系统参数一致性更好，四参数模型及其参数辨识结果只能在单一激励工况近似“等效”五参数模型。因此，五参数模型更可靠，可用于预测其余工况舵系统非线性动力学特性。

实际飞行中，存在舵面激励力矩幅值上百牛米的工况。五参数模型能计入激励力矩变化对摩擦力矩的影响，适用性更强。