Clough-Penzien 功率谱模型参数的识别与统计建模及应用

丁佳伟，吕大刚，曹正罡

（1.哈尔滨工业大学结构工程灾变与控制教育部重点实验室，黑龙江 哈尔滨 150090；2.哈尔滨工业大学土木工程智能防灾减灾工业和信息化部重点实验室，黑龙江 哈尔滨 150090）

引言

地震动是非常复杂且具有很强随机性的随机过程，其主要特性可以由幅值、持时和频谱三个基本要素来描述［1-2］。其中，地震动的频谱特性是指地震动对不同自振周期的结构反应特性的影响，在工程抗震中通常用傅里叶谱和功率谱来表示。地震动功率谱用来表征地震动的能量在各频段内分布的相对关系，可以进一步清晰地描述地面运动能量的频域分布规律，是地震动模型的重要组成部分［3-5］。对于功率谱模型的研究，最早是Housner［2］在1947 年提出的平稳白噪声功率谱模型，后来Kanai［6］将平稳白噪声过程经过一个阻尼比和圆频率分别为ξg和ωg的单自由度体系过滤后得到绝对加速度的功率谱，但是Kanai-Tajimi 谱严重高估了地震动的低频含量。作为地震学和地震工程学的重要内容之一，对功率谱模型的研究在过去的几十年内取得了令人瞩目的进展，多种改进模型被提出，如：C-P 谱［7］、胡聿贤-周锡元谱［8］、欧进萍谱［9］、杜修力谱［10］和洪峰谱［11］等，这些功率谱模型基本上都是对Kanai-Tajimi 谱的修正。

在随机地震反应分析中，一般采用功率谱密度函数表征地震地面运动，目前最大的难点就是地震动功率谱模型及其参数的确定。所采用的功率谱模型是否合理，参数是否准确，这将直接决定分析结果的可信度。在各类功率谱模型中，Clough 等［7］提出的C-P 谱利用了两个线性滤波器，可以过滤掉超低频率处的激励，从而改善了Kanai-Tajimi 谱不能反映基岩地震动的频谱特征以及过分夸大低频能量的缺点，具有明确的物理意义。但是，由于C-P 谱的参数较多且物理关系较为复杂，这在一定程度上限制了该模型的工程应用。因此，研究C-P 谱模型的参数识别方法及参数统计规律，对该模型在工程抗震中的广泛应用具有重要意义。

对于C-P 谱模型参数识别的研究，田利等［12-13］根据《电力设施抗震设计规范》（GB 50260—2013），采用普通最小二乘（Ordinary Least Square，OLS）算法对模型参数的取值进行了分析。柳国环等［14］、彭凌云等［15］均采用OLS 算法对功率谱模型参数进行识别。但是，OLS 算法对模型参数初始值的选取以及原始功率谱曲线的非线性要求高，这显然给大数据批处理统计分析制造了巨大的困难。为更加准确地保留原始功率谱的特性，寻求一种广泛适应性和快速收敛性的智能优化识别算法尤为重要。随着计算机技术的快速发展，越来越多的智能优化算法被应用于复杂的计算中，如遗传算法（GA）、蚁群算法（ACA）、粒子群优化算法（PSO）等，其中PSO 算法具有群体智能、内在并行性、迭代格式简单、可以快速收敛到最优解所在区域等优点，被广泛应用于函数优化、神经网络训练和模糊控制系统等领域。

在地震工程中进行结构动力时程分析时，需要选择合适的地震记录。《建筑抗震设计规范》（GB 50011—2010）［16］规定：采用时程分析法时，应按建筑场地类别和设计地震分组选用实际强震记录和人工模拟的加速度时程曲线，其中实际强震记录的数量不应小于总数的2/3。与真实地震记录相比，人工合成地震动能更有代表性地反映地震动的统计特征，并满足结构抗震设计需求，因此研究科学合理且高精度的人工地震动合成方法具有重要意义。

为解决上述问题，本文采用自适应加权粒子群优化（AWPSO）算法，对Clough-Penzien 谱模型的参数进行识别，然后从地震动数据库中挑选4159条地震记录并按照《建筑抗震设计规范》（GB 50011—2010）中的场地分类标准将其分组，采用AWPSO 算法对C-P谱模型进行参数识别，并依据K-S 检验、A-D 检验及AIC 准则和BIC 准则确定参数的最优概率分布模型。依据各参数间的相关性，建立Clough-Penzien 谱模型参数的联合概率密度函数。以Ⅱ类场地为例，对比分析规范场地转化功率谱与统计抽样功率谱的谱型差异，利用功率谱迭代修正的人工地震动合成方法，生成具有场地特性的地震记录，为地震危险性、易损性和风险评估以及工程结构抗震设计和评估等提供可靠的地震动输入。

1 Clough-Penzien 功率谱模型参数及识别方法

1.1 Clough-Penzien 功率谱模型及参数

Kanai-Tajimi 谱假定基岩地震加速度为白噪声，不能反映基岩地震动的频谱特征，且存在夸大地震动低频含量、不能求出地震地面位移、速度以及加速度的有限方差等缺点。Clough 等［7］提出的C-P 谱模型，其优点是利用两个线性滤波器，过滤掉超低频率处的激励，改善了Kanai-Tajimi 模型［6］过分夸大低频能量的情况，从而得到修正的模型如下：

式中ωg和ξg分别为场地的卓越圆频率和阻尼比；ωf和ξf分别为第二过滤层的卓越圆频率和阻尼比；ω为圆频率；S0为谱密度。

C-P 谱模型的随机参数向量θ为：

对于上述5 个参数的取值，目前学者们仅仅指出了ωf的取值应该小于ωg，建议ωf的取值范围为0.1～0.15 倍的ωg，ξf可以取与ξg相同的值，并没有依据真实地震记录给出场地可供参考的取值范围。

刘章军等［17］依据建筑抗震设计规范反应谱，给出了不同场地各参数的建议取值，但对于ωf的取值采 用0.1 倍 的ωg，ξf取与ξg相同的值，一方面由于第二个过滤层的参数设置的固定化，忽视了由于场地的随机性与复杂性所导致的功率谱模型参数的不确定性；另一方面由于规范反应谱对各类场地的5 倍特征周期以上的谱值已经进行了人为的放大，使谱值在不同周期段的概率特性、精度和协调性不一致，进而导致了规范反应谱并不能准确反映真实地震记录的时频特性。因此基于真实地震记录对随机参数向量θ进行精确识别和统计，给出不同场地各参数的取值范围，对工程抗震设计和评定具有重要意义。

1.2 基于自适应加权PSO 算法的参数识别

洪峰等［11］将Kanai-Tajimi谱模型非线函数化，然后利用OLS 算法确定参数，并给出了软土、中等土两类场地的参数识别结果。孔辰等［18］基于日本KiK-net强震数据库，采用上述方法对杜修力-陈厚群功率谱［10］进行了四类场地的参数识别。在对大量原始地震记录功率谱进行参数识别时，由于OLS 算法对数据的非线性以及拟合参数初始值的设置要求较高，一般预先对原始数据进行平滑化处理，以达到准确的识别结果。鄂国康等［19］利用移动平均算法对原始地震记录功率谱进行平滑化处理，然后采用OLS 算法确定功率谱模型参数。彭凌云等［15］也采用了类似的方法对不同功率谱模型进行参数识别，但移动平均算法有两大缺陷：一方面，平滑处理后的功率谱谱值与真实谱值之间存在一定的误差；另一方面，由于没有考虑结构的自振频率，无法实现不同频率区间采用不同窗口大小的功能。

目前研究人员可以利用不同的谱窗以及数字滤波器技术实现对功率谱的平滑化，无论何种方法，都是削峰填谷，使整体变得平滑，产生偏差是在所难免的。原始地震记录由于受到震源特性、传播路径和场地条件的影响，功率谱在频率上呈现出显著的多峰性、非平稳性和随机性的锯齿状，平滑处理后仅大致反映地震能量的平缓分布，消除了大量的随机性特征，保留了频谱的主体特性。因此，基于预平滑处理后和采用OLS 算法进行参数识别的误差平方和分别可以表示如下：

式中Sreal（ω）为原始地震记录的功率谱函数；Ssmooth（θ，ω）为经过平滑处理后的功率谱函数；SOLS（θ，ω）为OLS 算法参数识别后的功率谱函数模型。

OLS 算法的目标是寻找一组随机参数向量θ（ωgξgωfξfS0），使得观测值与理论值的残差平方和εtotal-OLS达到最小值。可以看到，采用传统OLS 算法进行参数识别存在两部分误差：一个是由平滑化处理引起的误差平方和εsmooth，另一个是OLS 算法参数识别产生的误差平方和εOLS。由此可见，两项误差源必定会导致总误差偏大，从而影响函数模型参数识别的准确性。

当前，越来越多的智能优化算法被应用于复杂工程问题的求解中，其中PSO 算法的应用最为广泛，它通过设计一种无质量的粒子来模拟鸟群中的鸟，粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向，粒子分别通过以下两个公式来更新自己的速度和位置：

式中νi，d（t）为粒子i在第t次迭代的速度；xi，d（t）为粒子i在第t次迭代中的当前位置；pbesti，d（t）为粒子i的个体极值点的位置；gbesti，d（t）为整个种群的全局极值点的位置；r1，r2为［0，1］之间的随机数；c1，c2为正的学习因子（加速系数）；d为维数；λ为惯性权重系数。

每个粒子在搜索空间中单独搜寻最优解，并将其记为当前个体极值，并将个体极值与整个粒子群里的其他粒子共享，找到最优的那个个体极值作为整个粒子群的当前全局最优解，粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置，其中粒子更新的方法如图1 所示。

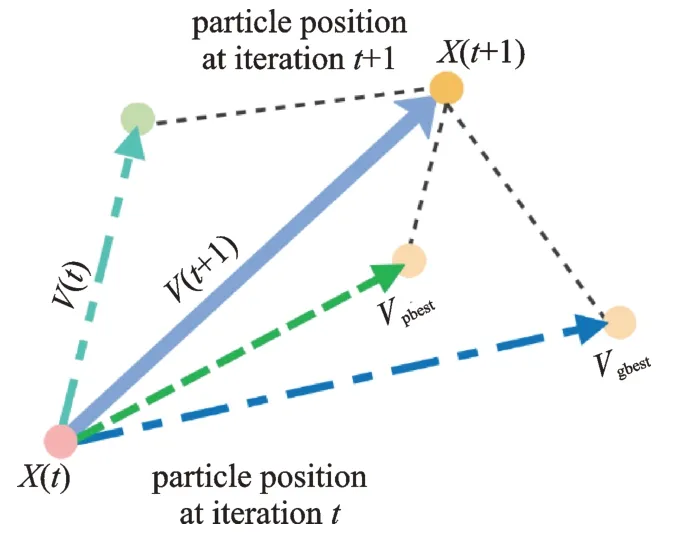
图1 粒子更新方法Fig.1 Particle updating method

为进一步提高粒子群算法的效率，研究发现：惯性权重系数λ可以影响微粒的局部最优能力和全局最优能力，较大的λ有利于提高算法的全局搜索能力，较小的λ会增强算法的局部搜索能力。为了平衡PSO 算法的全局搜索能力与局部改良能力，本文采用非线性动态惯性权重系数的粒子群优化算法，因惯性权重系数随微粒的目标函数值自动改变，故称此算法为自适应加权PSO（Adaptive Weighted Particle Swarm Optimization，AWPSO）算 法［20］，其中惯性权重系数λ的表达式为：

式中λmax和λmin分别为λ的最大值和最小值；f为微粒当前的目标函数值；favg和fmin分别为当前所有微粒的平均目标值和最小目标值。

由式（6）可知，当各微粒的目标值趋于一致或趋于局部最优时，惯性权重系数增大；而各微粒的目标值比较分散时，惯性权重系数减小。同时，对于目标函数值优于平均目标值的微粒，其对应的惯性权重系数较小，从而保留该微粒；反之，对于目标函数值差于平均目标值的微粒，其对应的惯性权重系数较大，使得该微粒向较好的搜索区域靠拢。因惯性权重系数随微粒的目标函数值而自动改变，所以此方法优于传统PSO 算法，可以更加快速地得到全局最优值。AWPSO 算法的流程如图2 所示。

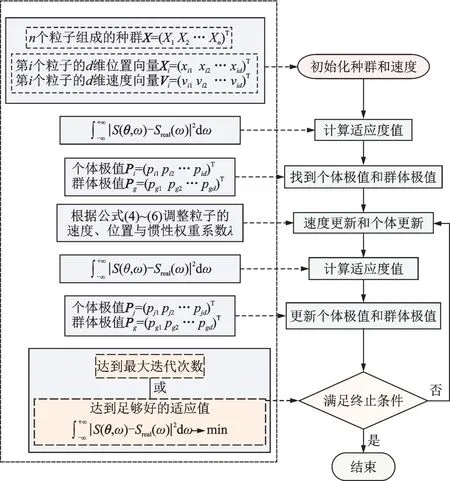
图2 AWPSO 算法流程Fig.2 Procedure of the AWPSO algorithm

本文利用上述方法对原始地震记录功率谱直接进行随机参数向量θ的识别，适应度函数如式（7）所示，满足残差的平方和最小。由于AWPSO 算法不需要进行平滑化预处理，因此，采用上述方法进行参数识别的残差平方和如下式所示：

式中Sreal(ω)为真实的功率谱谱值；SAWPSO（θ，ω）为使用AWPSO 算法进行随机参数向量θ识别后的功率谱函数模型。可以看出，采用此方法仅仅有一项残差平方和εAWPSO，对比OSL 算法参数识别，误差项仅有一项，且对原始数据非线性要求更低。

为了验证AWPSO 算法相较于普通最小二乘法识别的准确性与高效性，本文分别采用上述两种算法，利用两个典型地震记录El Centro 波和Taft 波的原始地震功率谱，进行C-P 谱模型随机参数向量θ的识别，其中，c1，c2均取2.0；λmax，λmin分别取0.9，0.4；最大迭代次数取500；种群粒子个数取100。图3（a）为基于上述两种方法对El Centro 波的识别结果，图3（b）为对Taft 波的识别结果。表1 分别给出了两种方法的绝对残差和与残差平方和。

表1 两种方法的拟合误差及精度对比Tab.1 Comparison of fitting error and precision of the two methods

图3 地震记录功率谱的参数识别Fig.3 Parameter identification of power spectra of seismic records

从图3 的对比中可以看出，两种方法均能够较好地拟合原始地震动功率谱，从Taft 地震波功率谱的参数识别中对比发现，相对于OLS 算法，采用AWPSO 算法参数识别可以保留更多的频谱主体特性，即在10 rad/s 附近可以更加清晰有效地表达出卓越频率处的能量分布，实现对功率谱更精准的拟合，对于结构随机振动分析和人工地震合成具有重要的意义。表1 分别计算了两种方法下不同地震波功率谱的参数识别精度，AWPSO 算法参数识别的绝对误差和及残差平方和均小于OLS 算法。采用下式计算AWPSO 算法相对于OLS 算法拟合精度的提升率：

结果表明，精度提高率μ均大于2.3%，采用AWPSO 算法的识别精度更高，优于传统的OSL 算法，同时计算效率也具有一定的提升，因此AWPSO算法在庞大的数据统计及随机参数向量θ识别方面更具准确性。

为避免过度拟合以及衡量统计模型拟合的优良性，假设模型的误差均服从独立正态分布，并采用赤池信息量准则（Akaike Information Criterion，AIC）精确评价拟合优度，如下式所示：

式中k为随机参数向量θ的维度；n为拟合数据的数量；SSR为残差平方和。

AIC的值越小，表明数据拟合结果越优。计算结果列于表1 中。可以看出，AWPSO 算法的AIC值均小于OLS 算法，从而进一步证明了AWPSO 算法对于随机参数向量θ的识别更具鲁棒性以及拟合结果的准确性，尤其对于具有明显卓越频率的功率谱随机参数向量θ的识别更具敏感性。因此，本文采用精确度高的AWPSO 算法对C-P 谱模型的随机参数向量θ进行大批量的参数识别及统计分析。

2 Clough-Penzien 功率谱模型参数的统计建模

鉴于C-P 谱模型具有明确的物理意义以及参数识别问题的复杂性，目前其取值并没有依据各类场地的真实地震记录给出可供参考的范围，从而限制了C-P 谱在随机振动分析中的广泛应用。本文采用图4 所示的流程，结合AWPSO 算法，给出了各类场地C-P 谱模型参数的取值范围和统计模型。

图4 随机参数向量θ 的识别统计流程图Fig.4 Identificatio statisticaln flow chart of random parameter vector θ

2.1 地震记录的挑选

本文利用太平洋地震工程研究中心（PEER）的NGA-West2 地震动数据库提供的强震加速度时程，选择其中信息较全且具有一定强度的地震记录。鉴于功率谱代表地震动的频谱特性，需要考虑震源特性、传播介质和场地条件三方面的影响来进行地震记录的挑选。

震级是体现震源特性的主要参数，ML和MS震级在一定的范围时却不再随地震释放额能量的增加而增加，出现震级饱和现象，这是由于震级标定本身存在严重缺陷，是不符合自然规律的。近年来得到广大应用的矩震级MW可以反映形变规模的大小，是目前量度地震大小最好的物理量，而且是一个绝对力学标度，对大震不产生饱和问题［21］。因此本文选取NGA-West2 地震数据库中具有明确矩震级MW标定的地震记录（4.0≤MW≤8.0）。

传播介质对地震动的频谱特性的影响主要指地震波在传播过程中的几何扩散和能量耗散吸收，常用距离项来表示，如震源距、震中距、断层距、Joyner-Boore 距等，其中Joyner-Boore 距是由Joyner等［22］于1981 年提出的，表示地面观测点到断层在地面投影的最短距离。因破裂带上距离场地最近的距离部分能够更清晰、可靠地表达传播途径对场地地震动频谱特性的影响，故本文选取地震记录时距离参数选用Joyner-Boore 距。

场地条件主要考虑场地类型对地震动的影响，本文依据文献［23］提出的抗震规范规定场地类型等效剪切波速与VS30的转化关系，将地震记录划分为5 类。

依据上述基本要求，确定下述原则从NGA-West2地震数据库挑选地震记录：①矩震级MW范围在4～8 之 间；②仅考虑Joyner-Boore 距 在30～600 km之间的地震记录，以排除近场地震动的影响，如方向性效应和脉冲效应都有可能主导地震动的频谱特性；③平均剪切波速符合《建筑抗震设计规范》（GB 50011—2010）［16］场地划分要求；④地震记录的PGA 在0.05～0.8g范围内；⑤均采用水平向的地震记录，不考虑竖向地震记录。其中，Ⅰ0类场地113 条；Ⅰ1类 场地982 条；Ⅱ类场地2300 条；Ⅲ类场地693 条；Ⅳ类场地71 条，共4159 条地震记录。图5 给出了Ⅱ类、Ⅲ类场地地震记录的矩震级MW与Joyner-Boore 距的关系。可以看出，每类场地地震记录的矩震级MW与Joyner-Boore 距分布相对比较均匀，可以排除由于数据集中分布导致统计结果缺乏说服力的问题，对地震记录的模型参数识别及其统计规律研究提供了良好的基础。

图5 不同场地矩震级（MW）与Joyner-Boore 距分布图Fig.5 Distribution of MW and Joyner-Boore distance at different sites

2.2 随机参数向量θ 的统计建模与检验

C-P 谱模型的随机参数向量θ是5 维向量，基于上述挑选的地震记录，采用AWPSO 算法对各类场地地震记录进行C-P 谱参数识别，其中AWPSO 算法的初始参数c1，c2均取2.0；λmax，λmin分别取0.9，0.4；采用最大迭代次数取500；种群粒子个数取100；设置随机参数向量θ的上下限：ωg∈（0，50），ξg∈（0，1），ωf∈（0，6），ξf∈（0，1），S0∈（0，20），充分保障计算结果的准确性。依据不同的场地类型，对随机参数向量θ的5 个分量分别进行识别统计。由于篇幅有限，图6 仅给出Ⅰ1类场地不同参数的概率密度直方图，其中纵坐标pdf表示概率密度函数。

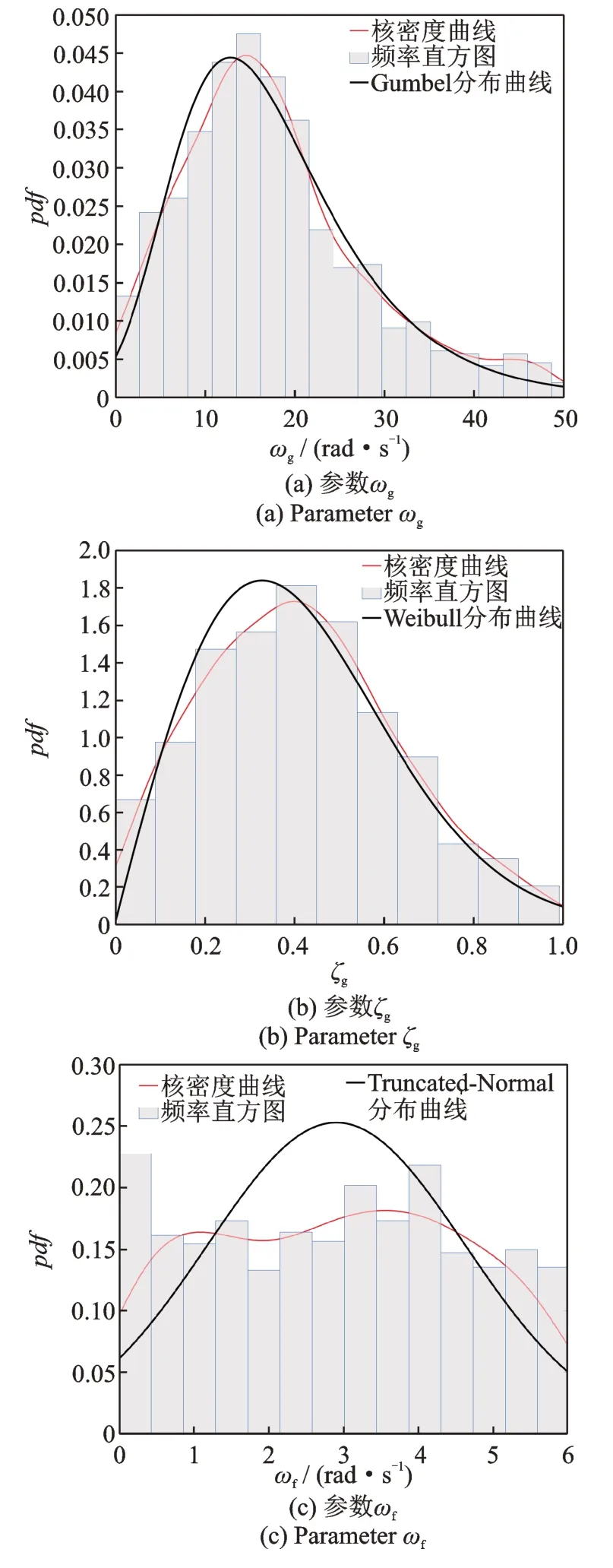
图6 Ⅰ1类场地C-P 谱模型参数分布直方图及概率分布模型Fig.6 Parameter distribution histogram and probability distribution model of C-P spectrum model for class Ⅰ1 site

利用上述识别的C-P 谱模型参数，分别对各参数进行统计分析，作出统计直方图。依据统计直方图，估计C-P 谱模型各参数的分布类型。本文分别选取截断正态分布（Truncated-Normal）、对数正态分布（Log-Normal）、极值Ⅰ型Gumbel 分布、偏移Gamma 分布和Weibull 分布五种概率分布形式作为备选概率分布模型。采用极大似然估计法获得谱参数的概率密度函数，然后分别对5 种概率分布模型在5%显著水平下进行K-S 检验和A-D 检验，以验证分布的合理性，当通过假设检验的模型多于一种时，则进一步采用AIC 准则和BIC 准则挑选出最优的概率分布模型。图6 为Ⅰ1场地C-P 谱参数的最优概率分布模型。

表2给出了不同场地类型C-P 谱参数的最优概率分布模型及其基本参数。其中，当谱参数的最优分布模型为Truncated-Normal 分布和Log-Normal 分布时，P1和P2分别代表（截断）均值和（截断）标准差；当谱参数的最优分布模型为偏移Gumbel 分布时，P1和P2分别代表位置参数和尺度参数；当谱参数的最优分布模型为Gamma 分布时，P1和P2分别代表形状参数和尺度参数；当谱参数的最优分布模型为Weibull 分布时，P1和P2分别代表尺度参数和形状参数。

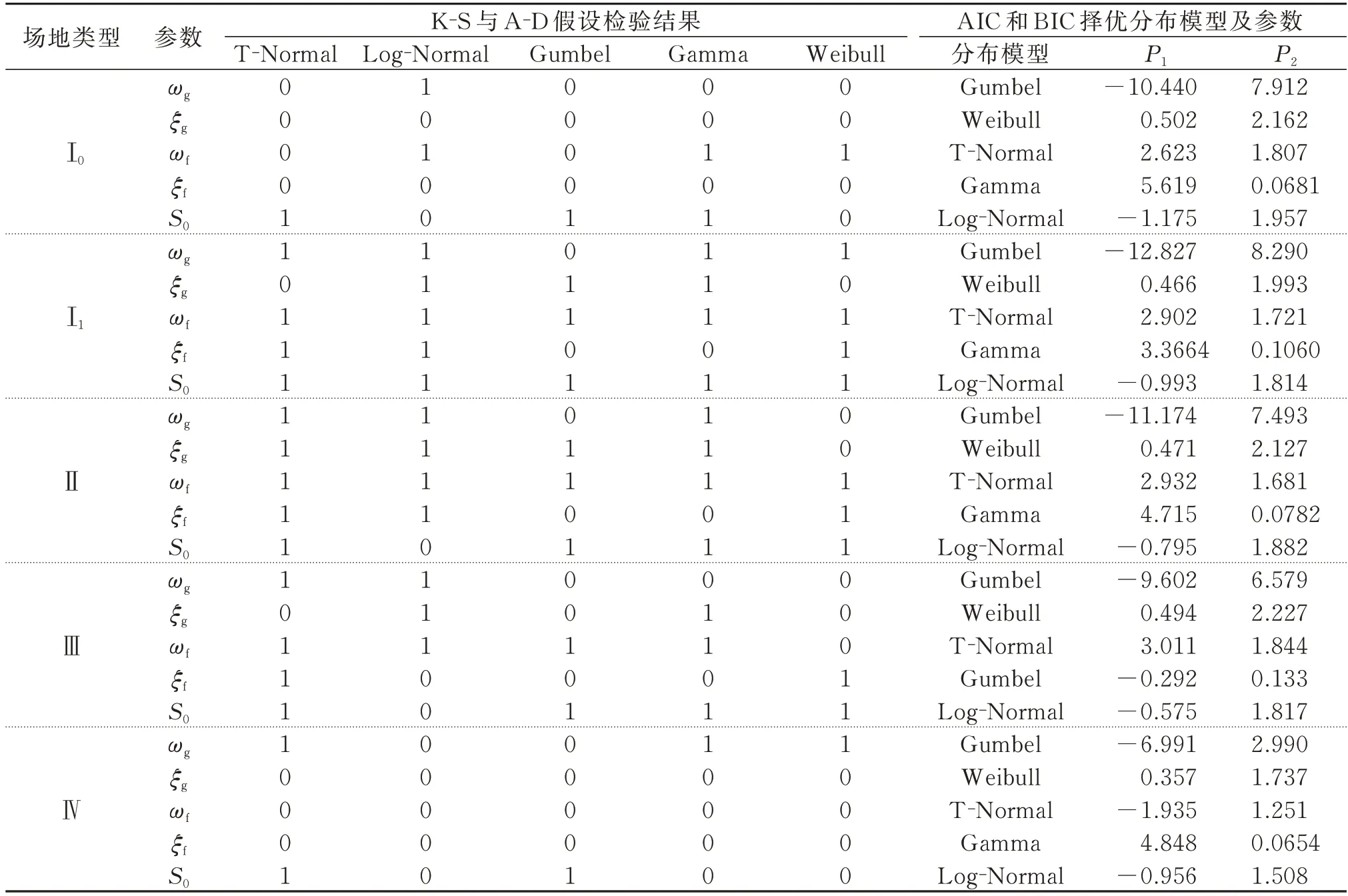
表2 各类场地C-P 谱模型参数的最优概率分布模型统计Tab.2 Statistics of the optimal probability distribution models of C-P spectrum model parameters for various sites

从表2 中可以看出，不同场地的参数服从不同的最优概率分布模型，对于以上5 种分布模型均未通过假设检验的参数，本文依旧给出了备选分布模型中置信水平最高且AIC与BIC值较小的概率分布模型。综合各种场地参数识别结果可以看出，ωg近似服从Gumbel分布，ξg基本服从Weibull分布，ωf服从Truncated-Normal 分布，ξf大致服从偏移Gamma分布，S0服从Log-Normal 分布。根据各参数的概率分布，可以进行Monte Carlo 抽样模拟，从而得出各类场地具有代表性的C-P 统计抽样功率谱，为不同场地的结构随机振动分析以及人工地震动合成奠定基础。

综合上述统计分析，依据各参数的最优概率分布模型以下四分位值与上四分位值作为建议取值范围，如表3 所示。通过比较5 类场地各参数的建议取值范围可以发现，ωg随场地类型的变化最大，随剪切波速的增大而增大，Ⅰ类场地明显大于Ⅳ类场地，导致这种现象的原因可能是坚硬土层相比于松软土层固有的卓越圆频率更高；ξg随场地的变化并不明显，大致在0.2～0.6 之间，由于第二个过滤层的参数主要体现在对低频的抑制作用，因此参数ωf与ξf受到场地特性的影响较小，ωf大致在1.5～4 rad/s 之间，且同一个场地ωf大约为0.1～0.25 倍的ωg，ξf建议取值在0.25～0.5 之间，基本与ξg保持一致。

表3 5 类场地各参数的建议取值范围Tab.3 Recommended value ranges for parameters of five types of sites

2.3 C-P 谱模型参数的相关性分析

为了构造C-P 谱模型参数的联合概率密度函数，本文进一步分析了随机参数变量θ中各参数之间的相关性强弱。选取3 种不同类型的相关系数：Pearson 线性相关系数、Kendall 秩相关系数、Spearman 秩相关系数：

式中x1i和x2i分别为随机参数向量θ中任意两个参数的第i个 值和分别为 它们的 样本均 值；N为样本容量；sign［•］为符号函数，其中当(x1ix1j)(x2i-x2j)>0 时，sign=1，否则sign=0；ri和si分别为向量θ中任意两个参数的秩和分别为它们的样本均值。

上述相关系数可以分别用来反映变量间的线性相关程度、一致性变化程度以及单调相关程度。

本文分别计算了5 类场地下随机参数向量θ各分量参数间的3 种不同相关系数。由于篇幅有限，本文仅给出了Ⅱ和Ⅲ类场地的3 种不同相关系数热图，如图7 和8 所示。

图7 Ⅱ类场地随机参数向量θ 的不同相关系数热图Fig.7 Heat map of different correlation coefficients for random parameter vector θ of class Ⅱ site

图8 Ⅲ类场地随机参数向量θ 的不同相关系数热图Fig.8 Heat map of different correlation coefficients for random parameter vector θ of class Ⅲ site

从图中可以看出，同一类场地中C-P 功率谱随机参数向量θ的任意两个参数之间，无论哪种相关系数，均小于0.8 的强相关阈值；其他场地也具有类似的特性。因此可以认为，随机参数向量θ各参数间存在弱相关性。基于上述分析，可以给出各单一随机参数变量的最优概率密度函数，进一步假设各变量是相互独立的，则C-P 谱模型的联合概率密度函数f（ωg，ξg，ωf，ξf，S0）可以表示为：

式中f（•）表示不同参数的概率密度函数。

3 基于Clough-Penzien 功率谱模型的地震动合成

基于得到的C-P 谱模型各参数的最优概率分布模型及联合概率密度函数模型，选择Ⅱ类场地作为典型场地进行分析，采用Latin 超立方抽样方法对每个参数进行106次随机抽样，并取其均值作为代表值。同时，根据Kual［24］提出的加速度反应谱值与谱矩在超越概率为r时的关系式，再通过对谱矩进一步近似后得到的由反应谱直接计算功率谱的近似表达式，当采用单边功率谱时，Kaul 的计算公式可以表示为：

式中Sa（ω）为地震动的功率谱；ξ为阻尼比；Pa（ω）为加速度反应谱；Td为强震动的持续时间；r为响应峰值超越反应谱值的概率，Kual 建议r近似取值为0.15。

利用上述Kual 近似转化公式，将规范Ⅱ类场地反应谱转化为场地统计功率谱，Ⅱ类场地转化统计功率谱与Latin 超立方抽样统计功率谱的对比如图9 所示，其中纵坐标PSD 表示功率谱密度。

图9 Ⅱ类场地功率谱对比Fig.9 Power spectrum comparison of class Ⅱ site

如图9 所示，场地规范转化功率谱在0 Hz 处值不为零，与实际不符；在低频处场地规范转化功率谱明显大于统计抽样功率谱，这是由于中国建筑抗震设计反应谱的长周期段（5 倍特征周期Tg至6 s）处的斜率为0.02 的直线，高估了长周期的反应谱值，但该下降段的谱值随周期延长下降过慢，且阻尼调整系数值过于保守；同时，下降段衰减指数高于美国和欧洲规范取值。从高层结构及隔震结构的实际应用来看，用规范设计反应谱求得的长周期结构地震作用较实际大［25］。除此之外，规范转化功率谱在高频处明显高于真实场地功率谱的谱值，造成这一现象的部分原因是Kual 近似转换公式在高频处的失真偏大，丁佳伟等［26］和何浩祥等［27］曾对这一现象做出了合理的解释，并对Kual 转化公式进行了修正，如图9 所示，修正转化后的功率谱与抽样统计功率谱在长周期阶段更加吻合，这是由于修正转化功率谱的计算源于真实的地震记录。综上所述，本文经过Latin 超立方抽样得到的统计功率谱在卓越频率处与场地规范转化功率谱十分接近，因此本文得到的抽样统计功率谱可以实现对场地总体特性的概括，并对场地规范反应谱的修正提供一定的基础。

在目前基于性能地震工程（PBEE）的实践中，输入的地震动主要来自过去的地震记录数据库。为了满足实际需求，需要调节所选择的地震记录，但调节后的地震记录并不能代表真实的地震记录，因此依据场地特性合成的地震记录更具代表性。如图9所示的Ⅱ类场地规范反应谱转化统计功率谱与Latin 超立方抽样统计功率谱，按照下式分别生成上述两种功率谱密度函数的强度非平稳随机过程样本函数：

式中φk为（0，2π）内均匀分布的随机相角；ωu，ωl分别为正ω域内的上、下限值，即认为Sx（ω）的有效功率在（ωl，ωu）范围内，而范围外的Sx（ω）值可视为零；f（t）为强度包络函数，体现了模拟地震地面运动的时间变化特征，是基于地震记录由上升、持续平稳到下降这3 个阶段的特性进行研究的，一般采用Amin等［28］提出的分段函数进行描述。

对于功率谱的修正迭代，本文采用文献［26］提供的方法，其迭代公式为：

式中j为功率谱迭代的次数，对第i个控制点周围的非控制点采用线性插值的方法进行修正；(ωi)为目标反应谱；Sa（ωi）为计算反应谱；Sj（ωi）为控制点的功率谱，达到误差允许的范围内即可停止迭代。

基于本文得到的C-P 谱参数概率分布模型，可以分别得到各类场地C-P 谱的函数模型，并依据功率谱迭代的人工地震动合成方法，合成具有场地统计时频特性的人工地震记录，如图10 所示。图11 计算了50 次随机模拟地震记录的平均反应谱与累计正斜率穿零点数的分布，其中纵坐标PSA 表示伪谱加速度。如图11（a）所示，合成地震记录的频谱在长周期阶段小于规范反应谱，这也符合真实地震记录的反应谱特性，因为本文提出的功率谱模型源于对不同场地真实地震记录的计算，并且中国规范反应谱的长周期的谱值偏大问题并没有解决，所以本文合成地震记录的反应谱的长周期谱值更具真实性。图11（b）通过累计正斜率穿零点数的分布进一步表征了合成地震记录的频域非平稳特性。综上所述，本文提出的合成地震动记录的方法无论是在时域还是在频域范围内，均具有良好的非平稳特性，从而可为工程结构的抗震分析、设计和评估提供可靠的地震动输入模型。

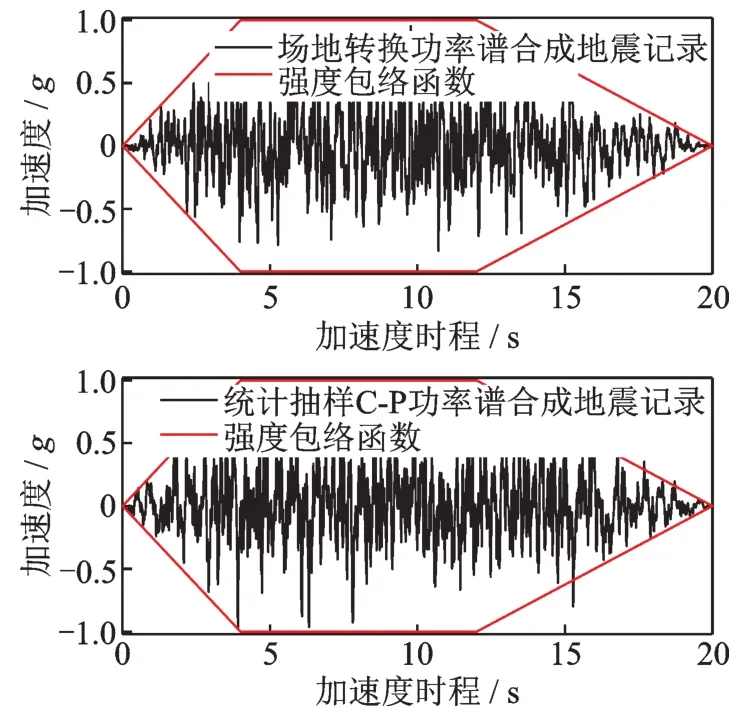
图10 基于不同功率谱合成的地震记录Fig.10 Synthesis of seismic records based on different power spectra

图11 模拟地震记录的频谱验证Fig.11 Spectrum verification of simulated seismic records

4 结论

Clough-Penzien 功率谱模型利用两个线性滤波器过滤掉超低频率处的激励，改善了Kanai-Tajimi谱不能反映基岩地震动的频谱特征以及过分夸大低频能量的缺点，具有更加明确的物理意义，但因其参数较多，学术界没有给出各参数依据具体场地真实地震记录的取值范围，限制了C-P 谱在结构随机振动分析以及人工地震动合成等地震工程中的应用和发展。

本文采用AWPSO 算法对C-P 模型的谱参数进行识别，通过对比分析发现AWPSO 算法的参数识别精度相比OLS 算法至少提升2.3%，且AIC值更小，进一步表明AWPSO 算法对数据拟合的可靠性，尤其在进行大数据处理中保障了参数识别的精度，同时该算法具有快速、高效等计算优势。

依据“震源特性-传播路径-场地条件”的地震记录挑选准则建立地震动数据库，利用AWPSO 算法分别对5 类不同场地的地震记录进行C-P 谱随机参数向量θ识别，并对各类场地不同参数进行统计建模，依据K-S 检验和A-D 检验以及AIC 准则和BIC准则确定参数的最优概率分布模型。采用3 种不同的相关系数，分别计算了各参数间的相关性，结果表明各参数间存在弱相关性，进而假设各参数相互独立，建立了C-P 谱模型的联合概率密度函数。

以Ⅱ类场地为例，依据给出的C-P 谱各参数最优概率分布模型，得到场地具有抽样统计意义的C-P 谱。相比于规范反应谱转换功率谱，无论在高频还是低频处，C-P 谱都更加符合真实的地震动频谱特性，也对反应谱的修正提供了参考。利用功率谱迭代修正三角级数合成人工地震动的方法，合成了具有场地抽样统计意义的C-P 谱地震记录，合成的人工地震记录具有真实场地特性地震记录的时/频域全非平稳特性，可为地震危险性、易损性和风险分析及工程结构抗震分析、设计及评估提供更为科学合理的地震动输入模型。