主动电磁轴承-柔性转子系统的不同位效应

李翁衡，祝长生

（浙江大学电气工程学院，浙江 杭州 310027）

引言

主动电磁轴承（Active Magnetic Bearing，AMB），简称为电磁轴承，是一种旋转机械转子新型的支承结构，通过可控的电磁力使转子稳定悬浮，具有无接触、无摩擦、无磨损、能在真空和高低温等特殊环境下应用等特点。得益于这些优点，电磁轴承被广泛应用于高速电机、压缩机、涡轮分子泵和飞轮储能等系统中［1-2］。由于受到转子材料机械强度的限制，为了满足设备高效率、高能量密度的要求，各类高速旋转机械的转子逐渐向更细、更长、转速更高的方向发展，这将导致转子运行在系统一阶或更高阶的弯曲临界转速之上。其中，工作转速超过其一阶弯曲临界转速的转子称之为柔性转子。

转子系统，无论采用何种传感器，由于结构及电磁兼容性的限制，都难以将传感器直接安装在AMB内部，因而产生了传感器中心的轴向位置与电磁轴承中心的轴向位置的不同位问题，这类系统被称为不同位系统。对于刚性系统，转子为刚体，利用简单的几何关系就能够从传感器位置测量到的转子振动信息中得到AMB 中心位置转子的振动信息。但对于柔性转子系统，由于转子振型的时变性，不可能通过简单的几何关系就从传感器位置测量到的转子振动信息中得到电磁轴承中心位置转子的振动信息。所以电磁轴承-柔性转子系统的不同位，不仅会影响转子系统的振动控制性能，还会影响控制系统的稳定性。

实际上，不同位现象在物理系统中广泛存在，早期一些学者对不同位结构的本质特征做了研究。Spector 等［3］研究了不同位结构模型的敏感性，他们发现系统中的零点对系统参数和边界条件的扰动比极点更为敏感。此外，传感器位置的微小变化可能导致零点和极点的顺序互换，从而使系统出现不稳定。Miu［4］对零点的物理含义做了研究，阐述了零点在确保控制系统稳定性方面的重要性，发现对于柔性结构，不同位系统的低阶模态由于相位相同，系统有交变的零极点对，但是其高阶模态可能出现不同相位，不一定有交变的零极点对。极点是系统的谐振频率，因此从稳定的角度看，同位系统的零点是非常重要的。从物理上看，当系统输出为零时，外部的能量被完全吸收并“困”在子结构的“内部储能元件”中，输出端检测不到位移，所以零点是这些子结构的谐振。

20 世纪90 年代，许多学者对AMB 系统的不同位进行了研究。Maslen 等［5］在传递矩阵法的基础上研究了一种将AMB 结合到柔性转子离散模型中的直接方法，该方法能设置传感器-执行器的不同位，所建的模型能方便地使用其他工具进行稳定性分析。Ramesh 等［6］指出用有限元法建立转子系统的模型可以方便地处理传感器的不同位问题，研究发现传感器从外侧向内侧移动时，第一阶临界频率增加，第三阶临界频率降低，同时第一阶临界处的振幅减小，第三阶临界处的振幅增加。Lefante［7］深入研究了柔性转子的不同位，用零极点交错和自由振型等开环特征来预测闭环系统的稳定性。首先，对于某阶模态，在无阻尼模态振型中若传感器位置的位移出现反相，此时闭环系统的对数衰减率也发生变化，由此得到了无阻尼振型与闭环系统稳定性的关系。然后，他指出零极点交错的系统可在任一补偿角度范围为0°～180°的相位补偿器的作用下达到稳定。但与同位系统不同，相位补偿器不能在不同位系统中提供无条件的稳定性。Obrzut［8］深入研究了不同位系统的动力学特性，发现如果把零点定义为反谐振频率，那么同位系统的反谐振频率在两个连续的反谐振频率之间，相位在0°～180°之间变化；不同位系统在两个谐振频率之间没有反谐振。虽然不同位系统每个谐振频率仍然有180°滞后，但没有因反谐振带来的180°超前，所以在第二次共振位置处会出现-270°的滞后现象。从增益根轨迹图发现，一旦不同位系统缺少反谐振，很小的增益就可能导致控制系统发散。此外，他还发现不同位系统会影响峰值位置，对临界转速也有影响。但是，这些工作中没有解释，对于一个柔性转子而言，只要是不同位系统就会有无穷多的不稳定模态，这会造成不同位系统就是不稳定的假象，而实际上AMB-柔性转子试验系统仍然是可以运行的。

从物理上调整传感器的位置能减缓不同位效应对转子特性的影响，满足转子正常运行的需求。Štimac 等［9］发现不同位效应影响到转子系统的第二阶弯曲模态，通过改变传感器的位置虽然可以解决二阶弯曲模态的问题，但不同位效应仍然影响着更高阶模态的特性。Schuhmann 等［10］提出了一种避免不同位问题的方法，即将电容传感器直接集成到径向磁轴承的定子铁芯中，利用卡尔曼滤波器来降低轴承线圈对传感器的噪声影响。Yu 等［11］研究了自传感技术，通过利用开关放大器的高频电流纹波进行调幅来估计转子位移，减少了元件数量。但工程应用上最成熟的仍是电涡流位移传感器。另外，也有不少学者试图从控制角度通过转子数学模型来解决不同位问题。Wang 等［12］考虑了不同位效应，提出一种模态分离策略，结合相位补偿器补偿不同位的影响。Geng 等［13］基于状态观测器的位移重构方法，结合相位补偿器，有效消除了电磁轴承-柔性转子系统的不同位问题，抑制了转子在跨越弯曲临界转速区的振动。这些研究均基于转子精确的动力学模型，并未能进行试验研究。在试验中仍缺少简单有效的方法来抑制不同位效应造成的发散，因此需要对这些抑制方法进行系统地论述。

本文首先建立了AMB-柔性转子系统的动力学模型；然后从转子动力学特性、开环传递函数的零极点、频率响应曲线以及闭环系统根轨迹等四个角度分析了AMB-柔性转子系统不同位对系统特性，特别是对系统稳定性的影响，提出了调节增益和插入式自适应陷波器等抑制由不同位导致不可控弯曲模态发散的方法；最后在试验台上进行了不同位条件下转子的悬浮、扫频、不平衡激励和旋转试验，对理论分析结论进行了试验验证。

1 AMB-柔性转子系统动力学模型

对于图1 所示的任意一个带有多个刚性圆盘的AMB-柔性转子系统，质量和刚度沿轴向是变化的，对这样的系统进行动力学分析，需要求解关于时间和空间的偏微分方程，因此通常采用离散化的方法进行建模。在转子上设n个节点，将AMB 的电磁力作为广义外力来看待，认为AMB 的电磁力是转子在AMB 节点所受的外力，只需将其叠加到AMB 位置转子节点广义力向量的对应位置处即可。

图1 AMB-柔性转子试验台Fig.1 Test rig of AMB-flexible rotor

用轴单元模型可以得到AMB-柔性转子系统的动力学方程为［14］：

式中M，D，G和K分别为4n×4n维质量矩阵、阻尼矩阵、陀螺矩阵和刚度矩阵；Ω为转速；Fmag为4n×1 维AMB 电磁力向量；Fu为4n×1 维不平衡力向量；Gm为4n×1 维重力向量；q为广义位移向量为广义位移的一阶导数；为广义位移的二阶导数。

AMB 的电磁力是线圈电流i和位移q的非线性函数。在工作点（q0，i0）附近进行线性展开，得到AMB 电磁力的线性化表达式为：

式中Fmag，0为静态悬浮工作点（q0，i0）的电磁力，一般情况下，Fmag，0刚好与系统的重力向量Gm平衡；i为控制电流向量；Ki为AMB 的电流刚度系数矩阵；Kx为AMB 的位移刚度系数矩阵。

由于AMB 在x和y两个方向上是耦合的，所以AMB-柔性转子系统是一个多输入多输出系统。为了利用多输入多输出系统的相关分析方法，可以将AMB-柔性转子系统的动力学方程（1）用状态空间方程表述为［14］：

当AMB-柔性转子系统的节点较多时，全阶模型的计算量很大。实际的AMB-柔性转子系统只需考虑较低阶模态的动力学特性，因此需要对AMB-柔性转子系统的动力学模型进行降阶处理。

应用模态截断方法［14］，如果只考虑转子的前r阶模态，存在模态转换矩阵Tm，使模态空间状态量qR转换成转子位移状态量q：

式中Tm为模态转换矩阵，Tm=[ϕ1ϕ2…ϕj]，其中，ϕj为转子系统的特征向量，j=1，2，…，r。

值得注意的是，模态截断方法的目的是减少计算量。模型的节点越多，保留的模态越多，转子的动力学特性就越复杂，但也就越接近实际的转子系统。

2 不同位效应

电涡流传感器及电感传感器是AMB 系统中最常用的转子位移传感器。由于传感器结构和电磁兼容性的限制，转子位移传感器一般只能安装在AMB的附近，由此产生了所谓的AMB 的中心位置和位移传感器的中心位置不重合的不同位效应，使得转子位移传感器的测量不能正确反映出AMB 处转子的位移，给系统的稳定性带来影响。

对于柔性转子而言，转子的弯曲状态随转速等参数发生变化，因此无法简单地从传感器处转子的振动推算出AMB 处转子的振动。在振型较为简单的低阶柔性模态情况下，与AMB 处转子的真实位移相比，不同位的信号表现为幅值有差，相位滞后的特征。若把振型复杂的高阶柔性模态考虑在内，如果有某一些模态振型的节点位于AMB 和位移传感器中间，当转子在对应的模态频率处以这样的模态振型振动，传感器处位移与AMB 处位移的相位相差180°，使得模态频率信号不能有效地衰减，对系统稳定造成隐患。

以下的数值和仿真分析是基于图2 所示的AMB-柔性转子模型进行的，它由1 根均质轴、2 个刚性圆盘及2 个AMB 轴颈组成，转子在径向上由2个AMB 支承。AMB 的相关参数如表1 所示。

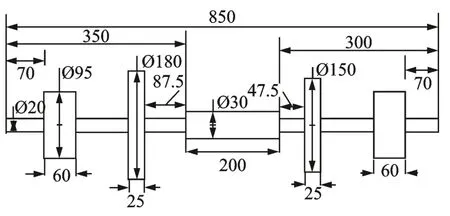
图2 柔性转子基本结构及尺寸（单位：mm）Fig.2 Basic construction and size of flexible rotor（Unit：mm）

下面从转子动力学特性、开环传递函数的零极点、频率响应曲线以及根轨迹四个方面来具体分析传感器与AMB 不同位对系统特性的影响。

2.1 转子系统的动力学特性

基于有限元法分析转子振型可以得到转子每一阶模态的节点信息。本文研究的柔性转子在静止悬浮的前5 阶弯曲模态振型如图3 所示。从各阶模态的振型图中可以看出，第五阶模态（三阶弯曲模态）和更高阶弯曲模态在传感器节点和AMB 节点之间存在模态振型与转轴中心线的交点（即模态节点）。柔性转子在0～15000 r/min（250 Hz）转速范围内，两端模态节点的变化如图4 所示。图4 的结果表明，在整个转速范围内，该三阶模态节点一直存在于传感器和AMB 之间，若该模态被外部激励激起，在传感器节点处检测到的模态频率分量与AMB 节点处的分量方向相反。

图3 柔性转子前五阶弯曲模态振型Fig.3 The first to five-order bending mode shape of flexible rotor

图4 不同转速下AMB 附近的三阶弯曲模态节点变化图Fig.4 Variation diagram of third-order bending mode nodes near the AMB at different rotational speeds

弯曲模态信号的衰减有两种方式：一为闭环增益小于1；二为控制器提供正确的反向控制且相位超前。第一种方式主要是因为二阶物理系统固有的信号衰减效应，是高阶模态一般不容易激起的原因。同位系统中不存在不稳定模态，因为在同位系统中，PID 在整个控制器带宽内都能使AMB 提供类似机械轴承的正刚度和正阻尼；而在不同位系统中，则需考察弯曲模态信号的衰减条件是否满足。

基于图2的转子在Simulink平台建立了AMB-柔性转子系统状态方程模型（式（3））进行研究，电磁力采用式（2）的线性化模型。

首先，分别向同位和不同位系统的AMB 的一个通道注入0～1000 Hz 的扫频电流，对扫频过程中转子对应通道的位移应用短时傅里叶变换进行时间-频域分析，提取其中逐渐发散的频率分量，其结果如图5 和6 所示。

图5 同位系统扫频结果Fig.5 Frequency sweep result of collocated system

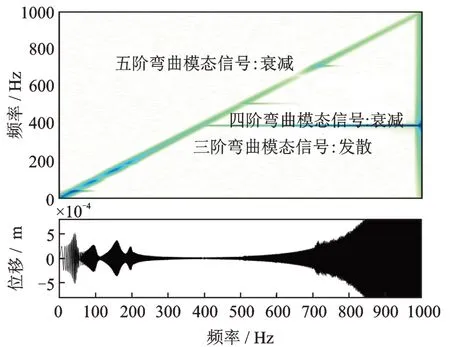
图6 不同位系统扫频结果Fig.6 Frequency sweep result of non-collocated system

通过对比图5 和6 可以看出，扫频电流依次激起各阶弯曲模态信号。一段时间后，同位系统的模态信号均能衰减，而不同位系统的三阶弯曲模态信号被激起后呈发散趋势。四阶和五阶弯曲模态虽然也受不同位效应影响，但因其频率高，闭环回路增益小，因此信号激起后逐渐衰减。因此，所研究转子的第三阶弯曲模态受到不同位效应影响最大，对系统稳定性影响也最大。

然后，进行恒速旋转仿真，对失稳过程中转子的位移进行时间-频域分析，其结果如图7所示。在静态悬浮时，不稳定频率分量为380 Hz；在转速为100 Hz时，不稳定频率分量约为340 Hz；在转速为150 Hz时，不稳定频率分量约为310 Hz。值得注意的是，虽然该柔性转子的转速较低，并没有跨越到第三阶临界转速，但低阶模态信号在仿真开始或起浮瞬间仍然能被激起。不受不同位影响的低阶模态（一阶、二阶弯曲）在PID的控制下迅速衰减，而三阶弯曲模态因不满足衰减条件而发散。

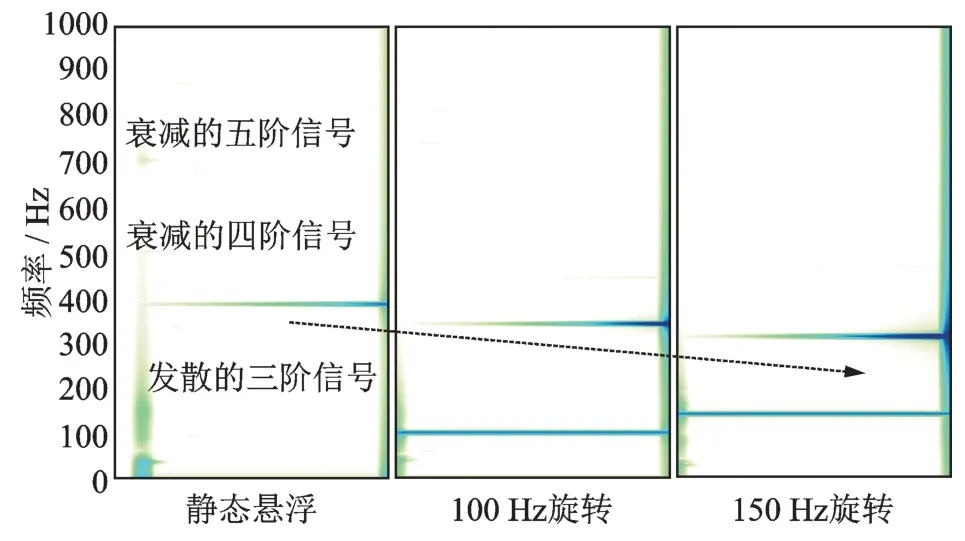
图7 不同转速下转子发散位移的时间-频域分析结果Fig.7 Time-frequency analysis results of rotor divergent displacement under different rotational speeds

基于AMB-柔性转子系统的动力学模型，可以计算得到转子系统在不同转速下考虑陀螺效应时的各阶正向及反向涡动频率［15］，如表2 所示。

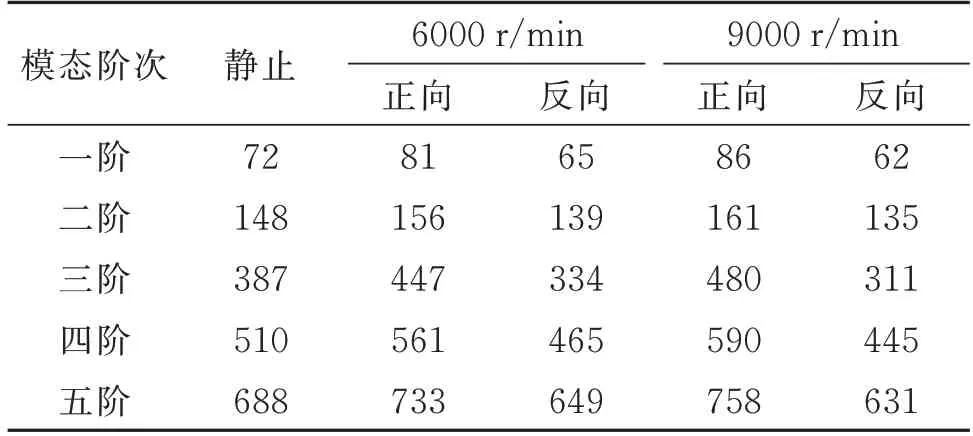
表2 柔性转子系统不同工作转速下的正、反向涡动频率（单位：Hz）Tab.2 The positive and negative vorticity frequencies of flexible rotor system at different working rotational speeds（Unit：Hz）

一般来说，除了转子与定子间的碰摩会引发转子的反向涡动外，不平衡激励不会激发转子系统的反向涡动。将表2 中柔性转子系统在不同工作转速下的正反向涡动频率与图4 中对失稳过程中转子的位移时间-频域分析提取出的不稳定频率进行对比可以发现，不同转速下的两个不稳定的频率分量刚好等于转子的第三阶弯曲反向涡动频率。因此，存在不满足衰减条件的不同位弯曲模态时，转子激发出对应模态下的反向涡动信号。

2.2 转子系统开环传递函数的零极点

根据AMB-柔性转子系统的动力学模型可以得到从电磁力输入到传感器位移输出的开环传递函数为：

式中s为拉普拉斯算子。

根据Cramer 法则，式（5）可写成：

那么开环传递函数的极点与零点分别为：

可见，转子系统的极点由质量、阻尼、陀螺矩阵、刚度等转子自身的动力学特性决定，与传感器位置无关。转子系统的零点不仅与转子自身动力学特性相关，还与AMB 的位置（Ts矩阵）和传感器的位置（Cm矩阵）有关。与同位系统相比，不同位系统仅改变了开环传递函数的零点位置和增益，不会影响系统极点的位置。

为了研究传感器位置对转子开环传递函数的零极点的影响，先不考虑陀螺效应，将传感器位置按图8 所示的方式，从两边逐渐向中间移动，其中，第④种情况为同位系统情形。转子从电磁力输入到传感器位移输出的开环传递函数的零极点图如图9所示。

图8 位移传感器的不同位置分析Fig.8 Analysis of different positions of displacement sensors

图9 中的叉代表极点，圆圈代表零点。转子的零极点图关于实轴对称，因此只列出零极点图中的正虚轴部分。对于每一张图，从下到上共有4 个极点和4 个零点，对应着一到四阶弯曲模态的频率。

由图9 可知，当传感器位置变化时，转子开环传递函数的极点位置始终不变，而零点位置改变。同位系统（序号④）传递函数的零极点交错出现，即零点-极点-零点-极点。而不同位系统（序号①～③和⑤～⑦）中，这种交错现象就被打乱。当某阶弯曲模态的节点位于位移传感器节点与AMB 节点中间时（称为“跨节点”），该模态对应的零点就会跨越到极点的另一边。如序号为①～③的三种情况，对应第三、四阶弯曲模态（跨节点）的零点转移到极点上方，与第一、二阶弯曲模态（不跨节点）的零点在极点下方恰好相反。

当考虑陀螺效应时，设定转速为6000 r/min，传感器和AMB 位置变化时对转子零极点的影响如图10 所示。由于陀螺效应的影响，虽然转子的各阶固有频率分化成前向涡动和反向涡动两个频率，转子每一阶均具有两对零极点。但不难发现，转子系统的零点移动方向与极点的相对位置均具有与不考虑陀螺效应影响时传感器不同位置下转子系统的零极点分布相同的规律。

图10 考虑陀螺效应时传感器不同位置下转子系统的零极点分布Fig.10 The zeros and poles distribution of the rotor system at different positions of sensors when considering gyro effect

2.3 转子系统开环传递函数的频率响应曲线

以电磁力为输入，位移为输出得到转子系统开环传递函数的响应伯德图如图11 所示。开环传递函数幅频响应曲线上的峰和谷分别对应传递函数的极点和零点，极点表示转子的固有频率，零点表示传感器检测到的位移为0 时所对应的频率，即转子振型刚好位于传感器位置时所对应的频率。

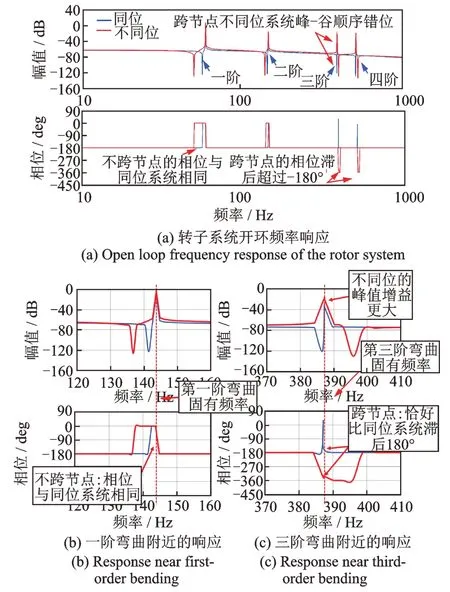
图11 转子系统的开环频率响应曲线Fig.11 Open loop frequency response curves of the rotor system

对图11 进行分析可得到如下结论：

（1）从固有频率处的峰-谷顺序来看，不同位系统中不跨节点的模态与同位系统相同，都是先出现谷，再出现峰，对应于先零点后极点的顺序；而不同位系统中跨节点的模态由于零极点相对位置相反，所以出现了先峰后谷的顺序。

（2）从临界区的相位上看，不同位系统中不跨节点的模态与同位系统相同，在幅频尖峰下降后迅速降为0，而跨节点模态没有上升过程，与同位信号保持有180°相位差，直至临界区结束。

因此，AMB-柔性转子系统开环传递函数频率响应曲线上先极点后零点的错位使得跨节点的相位在临界区有180°相位差。当转子振动时，对应的模态频率信号与传感器测得的转子位移信号刚好相反，这是不同位效应产生特殊相位行为的根源。

（3）从AMB-柔性转子系统整个开环传递函数幅频响应曲线来看，不同位系统的增益比同位系统更高，在尖峰处幅值更大。图12 为单通道注入电流激励的情况下，不同位效应导致转子系统位移信号发散过程中，传感器节点和AMB 节点输出的时间-频域图像。与AMB 节点对比，传感器节点（不同位信号）具有更多的高阶模态分量。

图12 不同位效应导致系统振动位移发散过程中的时间-频域图像Fig.12 Time-frequency image of divergent process of system vibration displacement caused by non-collocated effect

2.4 不同位系统状态方程分析

AMB-柔性转子系统动力学方程的状态空间方程为：

式中Am为模型降阶后的系统特征矩阵；Bm为输入矩阵；Bum为不平衡力输入矩阵；Cmm为位移传感器输出矩阵；Fum为降阶系统的不平衡力矩阵。

设分散PID 控制器的传递函数为：

式中Kp为比例系数；Kir为积分系数；Kd为微分系数；Ti为微分时间常数。

将单通道分散PID 控制器的传递函数改写为状态空间方程的形式：

转子系统的输出y为PID 的输入uc项，输出yc为转子系统的输入u项，合并四个通道的PID 方程，化简得到闭环系统的特征矩阵为：

式中Ac=diag［Ac1，Ac2，Ac3，Ac4］，Cc=diag［Cc1，Cc2，Cc3，Cc4］，Dc=diag［Dc1，Dc2，Dc3，Dc4］。

该闭环系统状态方程包括了四路分散PID 控制和完整的转子系统，属于多输入多输出系统分析，相比于传统简化成单路的单输入单输出传递函数分析，其充分考虑了转子系统x和y方向的耦合作用，更能反映出闭环系统的特性。

本文采用分次截断的方法分辨出各阶模态对应的特征值。闭环系统特征值的运动轨迹如图13 所示，符号曲线的颜色从浅到深表示转速从低到高。同位系统的前五阶特征值轨迹在左半平面，说明对于同位系统而言，简单的PID 控制就可以稳定系统的各阶弯曲模态。但非同位系统的第三阶和更高阶弯曲模态的特征值全部位于右半平面，处于不稳定状态，当这些不稳定模态信号的闭环增益大于1 时会影响系统的稳定性。

图13 同位和不同位系统的特征值沿转速的运动轨迹Fig.13 The motion trail of eigenvalues of collocated and non-collocated systems along the speed

3 不同位效应的抑制

为了稳定不同位系统，应抑制控制器对相关模态分量的增益，这通常有微分滤波、减小微分系数和低通滤波三种方法。

3.1 微分滤波

重写PID 中的微分环节的传递函数为：

式中N为滤波系数，与前述微分时间常数互为倒数对应。

在一般PID 控制器的设计中，为了得到理想的微分信号，通常将N取得很大，得到的PID 控制器在相当高频率时都有增益。为了抑制因高频增益过大导致的不同位系统的不稳定，应采取减小N的策略。

不同滤波系数N条件下PID 控制器的伯德图如图14 所示。N越小，PID 控制器对高频增益越低，但同时相位超前量小会引发阻尼不足的问题，特别是在跨越临界转速区时，若阻尼不足会引起强烈的共振。

图14 不同滤波系数N 的PID 控制器伯德图Fig.14 Bode plot of PID controller under different filter coefficients N

图15 为0～250 Hz 运行区间，不同滤波系数N的闭环系统特征值的运动轨迹。由图15 可见，滤波系数N取较小值能让位于右半平面的不稳定特征值向虚轴方向移动，等效于减小了这些不稳定模态的增益。但与此同时位于左半平面的稳定特征值也向虚轴移动，即削弱了这些模态的控制信号，造成稳定过渡过程变长。

图15 不同滤波系数N 的闭环系统特征值运动轨迹Fig.15 The motion trail of eigenvalue of closed-loop system under different filter coefficients N

3.2 减小增益系数

比例系数Kp影响PID 控制器全频段的增益，而微分系数Kd主要影响高频段的增益。在系统运行速度缓慢或在静态悬浮时，PID 控制器的增益主要由比例系数Kp决定；系统运行在柔性区间时，PID控制器的增益则主要由微分系数Kd决定。因此，对于运行在柔性区间的转子系统，减小微分系数Kd是一种有效的方法。

图16 为不同微分系数Kd的闭环系统特征值的运动轨迹。由图16 可知，小微分系数的作用与微分滤波相类似，能让位于右半平面的不稳定特征值向虚轴方向移动，减小了这些不稳定模态的增益。但与此同时位于左半平面的稳定特征值也向虚轴移动。这一方法实际上是通过辅助微分环节滤波来达到缩减整体微分增益的目的。

图16 不同微分系数Kd的闭环系统特征值运动轨迹Fig.16 The motion trail of eigenvalue of closed-loop system under different differential coefficients Kd

3.3 插入式自适应陷波器

为了降低控制器对不稳定模态的增益，可用陷波器有针对性地对某阶模态频率进行陷波。常用的陷波器为串联二阶陷波器，其传递函数表达式为：

式中α为阻尼因子，用于调节陷波器尖峰的陡峭程度；ωr为中心频率。

该二阶陷波器直接串联在PID 控制器后，若陷波频率较低时（400 Hz 以内），会对系统稳定性造成影响。为了避免此类问题，可采用插入式自适应陷波器。基于LMS（Least Mean Square）算法的自适应陷波器在t=kT时刻的迭代表达式为：

式中x为输入；u为步长；y为输出；T为采样时间；w1和w2为迭代权重系数。

插入式自适应陷波器的结构如图17 所示。

图17 插入式自适应陷波器的结构Fig.17 The structure of plug-in adaptive notch filter

串联二阶陷波器（α=1/6）和插入式自适应陷波器的控制器伯德图如图18 所示。可见两个陷波器的频率响应特性是类似的，但在试验应用时，若采用串联二阶滤波器，当陷波频率较低时，陷波器陷波频率之前的相位滞后可能会影响悬浮稳定，同时还会增加系统阶数。另外，输出不可限幅很有可能导致试验失败。插入式自适应陷波器应用了LMS 算法，其输出信号是以一个频率为算法中心频率的正弦波，不包括其他频率段的分量，因此不会对系统相位产生影响。可方便地对权重系数进行限幅，灵活调控输出以避免陷波器对系统产生影响。

图18 加入陷波器前后系统的伯德图Fig.18 Bode plot of system before and after adding notch filter

4 试验研究

为了验证AMB-柔性转子系统不同位效应的抑制方法，搭建了如图19 所示的AMB-多盘柔性转子试验台。两个AMB 安装在试验台两端的轴承座内部，电涡流位移传感器安装在轴承座侧边的端盖上。本文进行了静态悬浮、扫频、不平衡电流激励和旋转试验。

图19 AMB-柔性转子试验台Fig.19 Test rig of AMB-flexible rotor

4.1 静态悬浮试验

首先进行静态悬浮试验，偏置电流设定为1 A，PID 控制器设置一组初始参数（Kp=7，Kir=3，Kd=0.009），1 号轴承悬浮成功，2 号轴承x方向悬浮失败。系统的位移信号如图20 所示。尝试两次悬浮，均在系统即将运动到中点位置时发散而碰撞保护轴承。

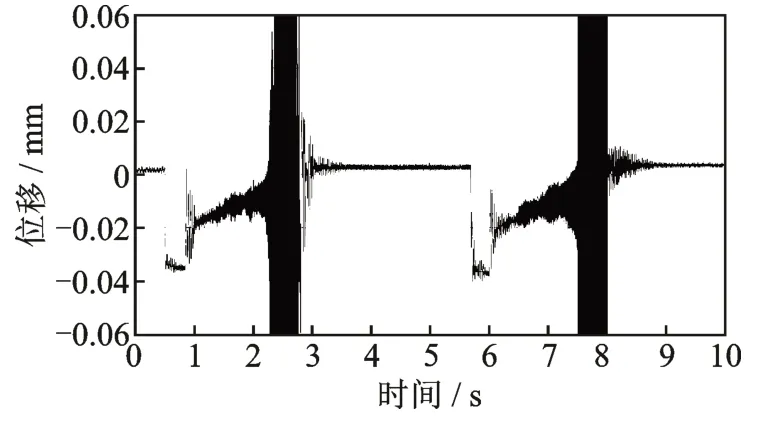
图20 系统悬浮失败的位移信号Fig.20 Displacement signal of system suspension failure

图21 为静态悬浮试验过程中转子位移信号的时间-频域分析结果。可以发现，发散的信号频率为第三阶模态的频率，且在控制过程中被反复激励，为失稳模态信号。

图21 系统悬浮失败的位移时间-频域分析图Fig.21 Displacement time-frequency analysis diagram of system suspension failure

多次调整参数后发现，只能采用小增益（Kp≤5.5）的方式才可以实现转子的静态悬浮，悬浮的位移信号如图22 所示。在悬浮时，Kp对第三阶模态信号影响大，Kd对第三阶模态信号影响小，为了稳定悬浮，必须将Kp减小。

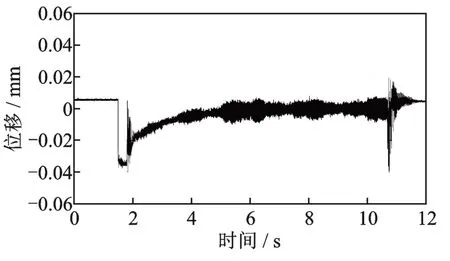
图22 小增益下系统悬浮的位移信号Fig.22 Displacement signal of system suspension under small gain

在系统临界发散时，启动插入式自适应陷波器，调节陷波器的中心频率至三阶模态信号附近，试验结果如图23 所示。结果表明，插入式自适应陷波器可在一定程度上衰减三阶模态信号，抑制系统发散。

图23 插入式自适应陷波器的试验结果Fig.23 Experimental results of plug-in adaptive notch filter

4.2 扫频激励试验

设定较小的PID 值稳定悬浮后，扫频仪依次向系统中的每个通道注入扫频电流，如图24 所示。

2 号AMB 的x方向扫频试验结果如图25 所示。在经过第三阶柔性模态频率时出现了发散失稳，导致扫频仪在350～400 Hz 获得的数据有误，停止控制信号重新悬浮才可恢复正常。扫频结果与仿真相符，说明受不同位影响的低阶模态对系统稳定性产生重大影响。

图25 转子扫频结果Fig.25 Frequency sweep results of rotor

4.3 模拟旋转的不平衡试验

在两个AMB 中施加干扰电流，以等效旋转过程中的不平衡激励。图26 为干扰电流的频率逐渐增大过程中转子的位移信号，在8 s 时开始加入模拟旋转的不平衡力，在34 s 时，不平衡激励接近300 Hz，系统出现剧烈振荡。为了研究减小增益系数能否抑制不同位效应，保持激励幅值和频率不变，分步调整Kp和Kd值，发现模拟旋转激励条件下，不稳定模态信号受Kd影响大，而受Kp影响小。最终，通过大幅度减小Kd值（Kd=0.0065），削弱了失稳现象。图27 为施加模拟不平衡激励过程中转子位移信号的时间-频域分析结果。可见失稳时激起了强烈的第三阶模态信号和其他模态信号。多次降低Kd的值后，发散信号逐渐减小，但对系统正常运行仍有明显影响。

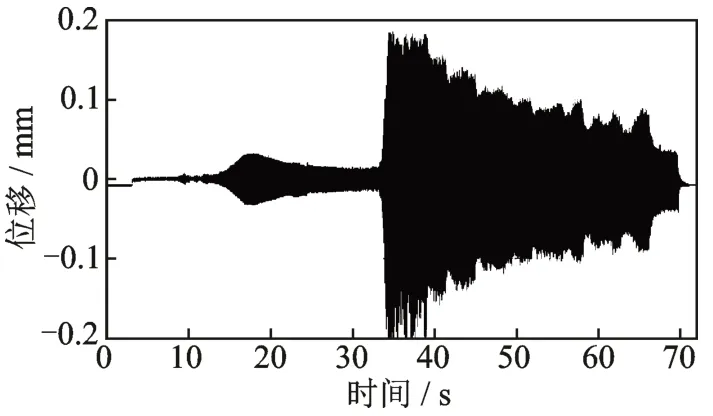
图26 施加不平衡激励的位移信号Fig.26 Displacement signal of applying unbalanced excitation

图27 施加不平衡激励的位移时间-频域分析图Fig.27 Displacement time-frequency analysis diagram of applying unbalanced excitation

静态悬浮和模拟旋转的不平衡试验的结果说明，不同位效应致使控制系统失稳，缩小了PID 参数可调范围。在静态悬浮或系统运行频率较低时，应减小比例系数；在系统运行频率较高时，应减小微分系数。

图28 为加入300 Hz 模拟不平衡电流时，改变微分滤波系数的结果。从N=2000 的发散状况开始，逐渐降低N的数值，直到N=800。可见与减小Kd的效果相似，发散在一定程度上被抑制。

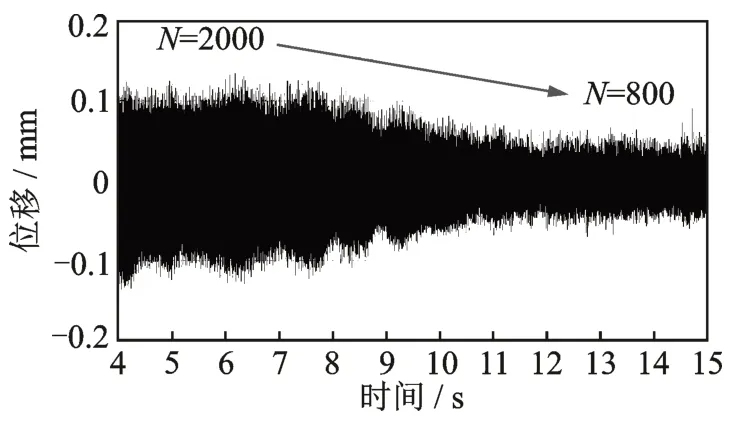
图28 改变滤波系数N 的位移信号Fig.28 Displacement signal with different filter coefficients N

4.4 旋转试验

为了验证不同位效应会激起反向涡动，下调偏置电流至0.5 A，将Kp调至4.5，Kd调至0.0065，可让转子在小刚度下稳定运行并跨越二阶弯曲临界转速至最高运行转速250 Hz。2 号轴承的x方向在升速和降速过程的振动如图29 所示，时间-频域分析如图30 所示。

图29 转子升速和降速过程的振动曲线Fig.29 Vibration curves of rotor accelerating and decelerating process

图30 转子升、降速过程的时间-频域分析图Fig.30 Time-frequency analysis diagram of rotor accelerating and decelerating process

从图30 中可以看到，在小刚度下，转子位移中仍然含有三阶弯曲模态信号。在转子开始加速时，三阶模态信号分为两支，其中随着转速上升而升高的前向涡动分支信号很小，而随着转速上升而降低的反向涡动分支信号较为明显。当转子各倍频与该反向涡动分支信号相交时，交点颜色变深，证明转子倍频会激发三阶弯曲模态的反向涡动。但由于此时刚度小，闭环增益小，激发起来的不稳定信号很快在回路中被削减，没有影响稳定性。

5 结论

在电磁轴承支承的柔性转子系统中，由于各种因素的限制，转子的位移传感器无法安装在电磁轴承的中心位置，因而产生了传感器中心位置与电磁轴承中心位置不同位。本文从转子动力学特性、开环传递函数的零极点、频率响应曲线以及根轨迹等四个方面分析了传感器与电磁轴承不重合的影响；然后提出了不稳定模态信号的抑制方法；最后，对不同位效应的影响和抑制方法进行了试验验证。理论和试验结果可得到以下结论：

（1）高阶模态信号的稳定具有两个方式，高阶模态信号在二阶物理系统得到自然的衰减，而低阶模态信号需要控制器提供反向控制和相位超前。

（2）受不同位效应影响的弯曲模态振型节点位于传感器和电磁轴承之间，导致转子系统的开环传递函数零极点交错的规律被破坏。该模态信号分量一旦被激起，就存在不能得到衰减的可能性。

（3）受不同位效应影响的弯曲模态对应频率下的闭环增益大于1 时，将会发散而导致失稳，发散信号为反向涡动模态信号。

（4）抑制不同位效应的方法主要是降低控制器对不稳定弯曲模态的增益，本文提出的降低刚度、减小PID 参数和采用插入式自适应陷波器的方法，可有效抑制不稳定模态信号的发散。