计入结构柔性的风电齿轮箱行星轮系动力学特性研究
谭建军,李 浩,冉 峯,朱才朝,宋朝省,李祖锋
(1.重庆大学机械传动国家重点实验室,重庆 400044;2.重庆工商大学智能制造服务国际科技合作基地,重庆 400067)
引言
在“十四五”期间,中国风电补贴国家政策将全面取消,对风电机组度电成本提出了严苛要求,而发展10 MW 及以上超大功率风电机组是降低度电成本的有效措施之一[1]。具有多行星轮功率分流的风电齿轮箱被广泛应用于风电机组中传递兆瓦级功率,是极为重要的传动装置。为了满足更大功率的传递需求,风电齿轮箱行星轮系内齿圈和行星架等构件尺寸将会设计得更大,行星轮数量也将增多,容易在随机气动转矩作用下产生过大的系统振动噪声和动载荷,增大疲劳失效风险。因此,开展计入结构柔性的风电齿轮箱行星轮系动力学特性研究具有重要意义。
国内外学者围绕行星轮系动力学建模、固有特性和动态响应等开展了深入研究,取得了诸多有益的研究成果。Lin 等[2]利用行星轮系动力学模型分析了轴承支撑刚度、齿轮副啮合刚度等设计参数对系统固有频率与模态动能的影响,发现了模态跃迁现象。Eritenel 等[3]分析了行星轮系自由振动模态,将行星轮系振动模态归纳为三类振动模式,即中心构件扭转、中心构件平移和行星轮振动模式。Guo等[4-5]考虑时变啮合刚度、非线性齿面接触和轴承游隙等时变参数激励,分析了行星轮系非线性振动特性。Zhai 等[6]考虑时变行星架装配误差,建立了多级行星轮系动力学模型,分析了行星轮系动态啮合力。Öztürk 等[7]以弹性力学为基础建立了行星轮系纯扭转动力学模型,研究了轮齿修形对行星轮系振动特性的影响。为了提高行星轮系动力学模型计算精度,Parker 等[8]将内齿圈视为弹性连续体,建立行星轮系弹性-集中参数混合动力学模型,分析了行星轮非均布对系统固有特性的影响,在常见的三类振动模式[3]基础之上,发现了内齿圈的弯曲振动模式。Fan 等[9]、Guan 等[10]采用壳理论 和Timoshenko 梁理论计算内齿圈结构柔性,建立行星轮系壳/梁单元-集中参数混合动力学模型,分析了内齿圈动态变形和系统固有特性。Kahraman 等[11]采用有限元法建立了行星轮系准静态分析模型,分析了内齿圈柔性对构件动应力和变形的影响。张俊等[12]将连续体柔性内齿圈离散为多段等效虚拟弹簧连接的刚性内齿圈段,研究了内齿圈柔性对系统固有特性的影响。许华超等[13]采用平面梁单元建立弹性边界柔性直齿内齿圈的振动分析模型,分析了组合激励下系统固有特性。魏静等[14]采用轴系单元将内齿圈和行星架进行离散化建模,研究了内齿圈和行星架结构柔性对多级行星轮系动态啮合力的影响。为了考虑复杂结构几何特征,Abousleiman 等[15]、Portron 等[16]考虑内齿圈柔性,采用有限元法建立了行星轮系有限元-集中参数混合动力学模型,分析了系统振动特性。Bettaïeb 等[17]、Guilbert 等[18]将模态综合法引入到定轴齿轮动力学建模中,有效提高了建模精度,并降低了系统自由度。随后,许华超等[19]采用有限元-集中参数混合方法建立计入传动轴和机匣结构柔性的直升机主减速器混合动力学模型,研究了机匣结构对系统振动特性的影响。
目前,行星轮系动力学建模方法可以大致划分为集中参数模型[2-7,12]、混合模型[8-10,13-19]和有限元模型[11]。集中参数模型侧重于对系统固有特性、激励机理及动态载荷分配等进行初步分析,在建模时常将齿轮、轴和轴承简化为一体,以简单径向、弯曲和扭转刚度代替弹性轴的复杂受载状况。此类模型未计入内齿圈、行星架和箱体等构件的弹性变形,整体计算精度不高。混合模型包括梁/壳单元-集中参数混合模型和有限元-集中参数混合模型,由于此类建模方法在集中参数模型的基础之上计入了内齿圈、行星架和传动轴等构件的弹性变形,整体计算精度得到提高。相比于梁/壳单元-集中参数混合模型,有限元-集中参数混合模型可以考虑复杂的结构几何特征,适用性更好,但多用于恒定转速下的振动分析,少有文献关注计入内齿圈结构柔性的行星轮系变速变载动力学建模。此外,集中参数模型和混合模型常将齿轮副多轮齿啮合简化为等效单点啮合,以简单的综合啮合刚度代替复杂的多轮齿啮合过程,造成在求解轮齿动载荷时精度不高。有限元模型可以考虑复杂结构几何特征,并能较好地模拟轮齿接触状态,全面反映行星轮系各构件受载状况,但此类模型建模过程复杂、计算量庞大、系统级建模分析困难,一般不适用于动态设计场合。
综上所述,为了提高变速变载工况下风电齿轮箱行星轮系动力学性能的预测精度,针对常规梁/壳单元无法考虑复杂构件几何特征、计算精度低和大规模有限元计算量大、系统级建模分析困难的问题,基于有限元-集中参数混合模型,提出一种计入结构柔性的行星轮系变速动力学建模方法。以某型5 MW 级风电齿轮箱低速级行星轮系为研究对象,采用有限元缩聚理论对内齿圈和行星架进行建模,并将齿轮啮合副常规等效单点啮合细化至多对轮齿啮合,建立能够反映复杂构件几何特征、轮齿动载荷且适用于变速运行的行星轮系动力学模型,为风电齿轮箱行星轮系动态设计提供理论基础。
1 行星轮系动力学建模
1.1 子结构缩聚单元
由于实际工程结构往往较为复杂,整体结构有限元模型节点自由度数量庞大,造成计算效率低、收敛慢等问题,因此常采用子结构缩聚方法消除“整体单元”中除需要保留节点以外的所有节点自由度,将子结构系统矩阵规模缩减至可接受的维度。
建立如图1 所示的行星架(c)和内齿圈(r)有限元模型,根据其结构特征,在其连接位置、轴承支撑和内齿圈轮齿处设置缩聚点,包括行星架的驱动力矩(缩聚点1)、轴承支撑(缩聚点2 和3)和销轴(缩聚点4~8);内齿圈的轮齿(缩聚点1~93)、箱体连接(缩聚点94 和95)和螺栓连接(缩聚点96~120)。定义如图2 所示的O-XYZ为原点固定在内齿圈中心的绝对坐标系;orj-xrjyrjzrj为原点固定在内齿圈轮齿缩聚点和螺栓连接缩聚点的绝对坐标系,且与O-XYZ平行;oc-xcyczc为原点固定在行星架中心并随其转动的随动坐标系;ocpi-xcpiycpizcpi为原点固定在销轴缩聚点并随行星架转动的随动坐标系,且与oc-xcyczc平行。此外,内齿圈缩聚点94 和95 参照O-XYZ;行星架缩聚点1~3 参照oc-xcyczc。Rc为太阳轮到行星轮的中心距离,ϕpi为行星轮i的位置角。
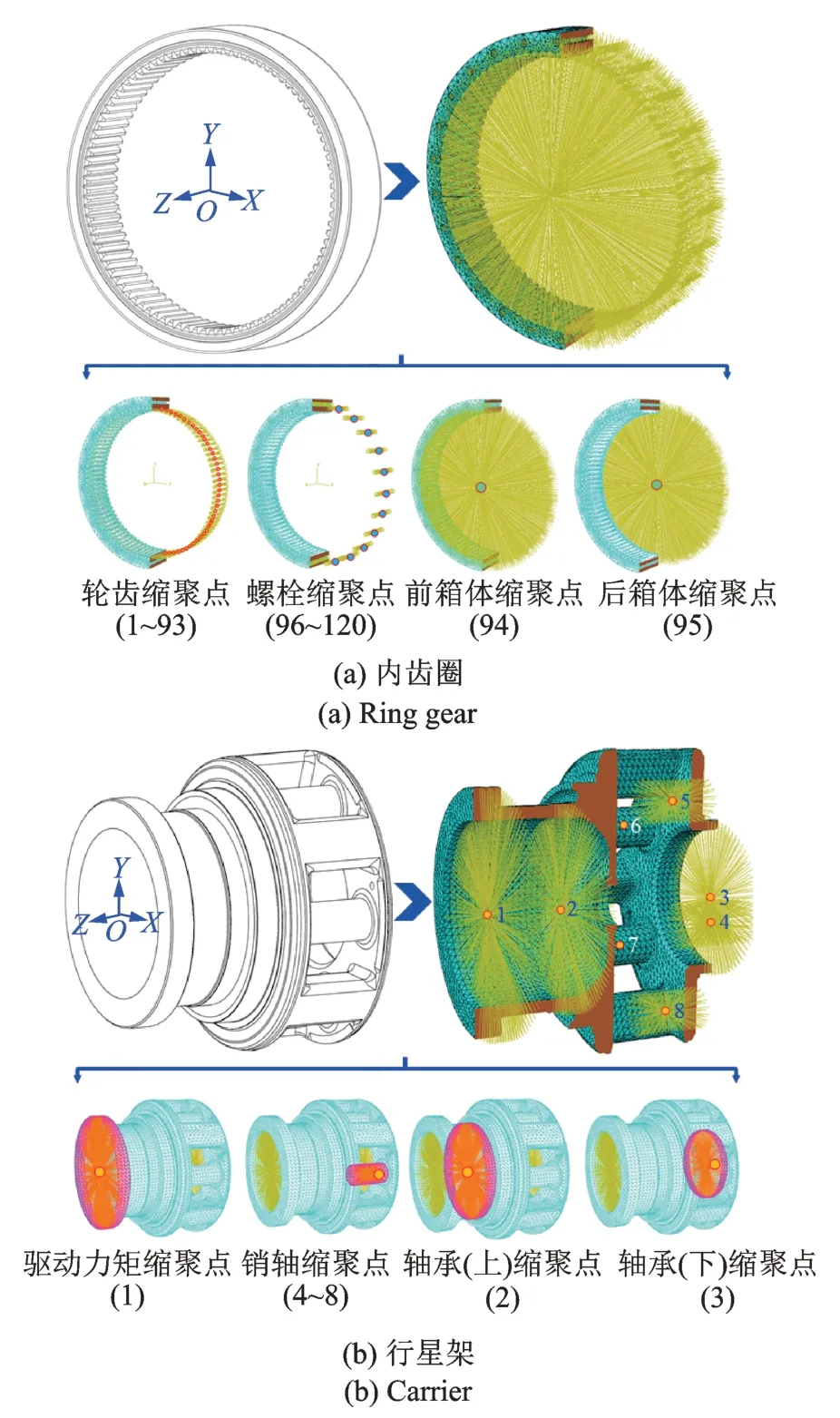
图1 有限元缩聚模型Fig.1 Finite element condensation model

图2 缩聚点坐标系定义Fig.2 Definition of coordinate systems of condensation points
内齿圈轮齿缩聚点设置在每个轮齿节圆且位于齿宽中心位置处,则根据角度可以计算出任意内齿圈轮齿节点在O-XYZ中的坐标如下式所示:
式中Rmr为内齿圈节圆半径;ϕrj为内齿圈轮齿节点j的位置角。
同理可得螺栓连接缩聚点坐标,不再详述。
通过柔性多点约束(MPC)[20]将缩聚点与对应的界面节点进行连接,采用固定界面模态综合法对行星架和内齿圈进行子结构缩聚,可得缩聚后构件χ(χ=r,c)在自身参考坐标系下的位移向量为:
可得缩聚后行星架和内齿圈的自由振动方程为:
1.2 啮合与支撑单元
采用如图3 所示的广义坐标系对太阳轮和行星轮进行建模,包括太阳轮随动坐标系os-xsyszs和行星轮随动坐标系opi-xpiypizpi,xpi和ypi分别为行星轮径向和切向方向。行星轮中心与对应的行星架销轴缩聚点重合,行星架缩聚点转动自由度(υ取值参考图1(b))参照O-XYZ,其余自由度参照oc-xcyczc和ocpi-xcpiycpizcpi(见1.1 节)。Rbs,Rbp和Rbr分别为太阳轮、行星轮和内齿圈的基圆半径。图4 所示为行星轮系啮合副中轮齿动态啮合点Mc在啮合平面上的位置。

图3 行星轮系啮合副Fig.3 Meshing gear pairs in the planetary gear train
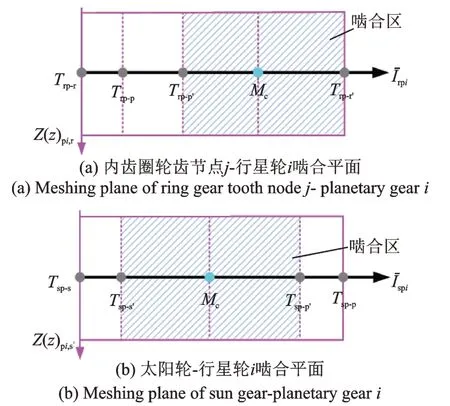
图4 行星轮系啮合平面Fig.4 Meshing plane of the planetary gear train
1.2.1 啮合单元
基于δspi(Mc)和(Mc),可得太阳轮-行星轮i啮合副、内齿圈轮齿节点j-行星轮i啮合副在啮合点Mc处时,各构件6 个自由度广义位移向啮合线方向转化的投影矢量分别如下式所示[22]:
然而,在文献[2-14,17-19]中太阳轮-行星轮啮合副和内齿圈-行星轮啮合副常采用等效综合啮合刚度将啮合副中多轮齿啮合过程简化为等效单点啮合,其啮合刚度矩阵Ksp(Mc)和Krp(Mc)分别如下式所示:
式中Np为行星轮数量;Λ为定位矩阵,即将啮合刚度矩阵扩展至整个系统矩阵;Kspi和Krpi分别为太阳轮-行星轮i啮合副、内齿圈-行星轮i啮合副的综合啮合刚度;Vspi和Vrpi为对应的啮合向量,并未细化至每对啮合轮齿。
啮合阻尼矩阵Csp(Mc)和Crp(Mc)的形式分别与式(7)和式(8)相同,其中啮合阻尼采用经验公式计算,见文献[23]。
基于式(7)和(8),按照“化整为零”的思想,将齿轮副综合啮合刚度按照其重合度等效分解到每对啮合轮齿上,同时为了模拟每对啮合轮齿从啮入到啮出的状态变化,引入轮齿啮合判断系数和可得:
式中Nr为内齿圈齿数;为太阳轮-行星轮i啮合副中参与啮合的第l对齿啮合刚度;为第j个内齿圈轮齿节点在内齿圈-行星轮i啮合副中对应参与啮合的第l对齿啮合刚度;ceil(∙)为朝正无穷大方向取整;ξ为重合度;为太阳轮-行星轮i啮合副中参与啮合的第l对轮齿啮合向量;为内齿圈轮齿节点j-行星轮i啮合副中参与啮合的轮齿啮合向量。
式中lspi∈[1,ceil(ξspi)],lrpi∈[1,ceil(ξrpi)]。
在啮合区内(见图4),啮合点从啮入到啮出刚好经历一个单对齿啮合刚度变化周期,可得:
式中Tspi和Trpi为单对齿啮合刚度变化周期;pbt为基圆节距。
1.2.2 支撑单元
行星架销轴缩聚点与行星轮通过轴承支撑单元耦合,但销轴缩聚点的参考坐标系与行星轮节点不一致,需要采用旋转矩阵Tcp[26]将销轴缩聚点的广义位移向量转换至坐标系opi-xpiypizpi:
基于式(15),可得销轴缩聚点与对应行星轮节点的耦合刚度矩阵Kcp为:
1.3 轴段单元
结合如图5 所示的太阳轮轴结构特征,采用计入剪切变形影响的修正Euler-Bernouli 梁单元[27],建立轴段梁单元动力学方程。其中,第J个梁单元包括2 个节点,每个节点考虑6 个自由度,定义在自身参考坐标下的广义位移向量为:

图5 太阳轮轴段单元建模Fig.5 Modeling of sun shaft segment
可得第J个梁单元自由振动方程为:
1.4 激振力单元
齿形误差是齿轮制造加工中产生的典型高频误差,在齿轮啮合过程中表现为周期性位移激励,可以通过三坐标测量机等仪器实测获取。本文仅考虑单齿切向偏差,其与齿轮啮频相关,将其视作简谐函数[23],可得齿轮副啮合误差表达式为:
此外,结合式(9)和(10),可得由内齿圈虚拟振动线位移Rbr产生的激振力矩阵为:
同理,可得由齿轮啮合误差产生的误差激振力矩阵,不再详述。
1.5 系统耦合模型
根据如图6 所示的太阳轮、内齿圈、行星架和行星轮节点自由度及其耦合关系,定义系统节点在自身参考坐标下的广义位移向量为:

图6 行星轮系耦合模型Fig.6 Coupling model of the planetary gear train
将太阳轮、内齿圈、行星架和行星轮的质量矩阵、刚度矩阵与阻尼矩阵按照式(21)所示顺序进行组装,建立行星轮系动力学模型:
式中Msys,Ksys和Csys分别为系统质量矩阵、刚度矩阵和阻尼矩阵;Fsys为系统激振力矩阵,包括输入扭矩(Tin)、误差激励、内齿圈虚拟振动线位移激励和负载(Tout),其中负载根据太阳轮转速对转速-转矩运行特性曲线进行插值得到[29]。
行星轮系动力学模型,共计138 个节点+120 阶内部节点保留模态,948 个自由度。
由于模型自由度数量较大,造成行星轮系动力学模型求解困难,本文采用精细积分法(PIM)[30]求解式(22),计算各节点振动位移和振动速度,步长取为1×10–5。
2 结果分析与讨论
某型5 MW 级海上风电齿轮箱低速级行星轮系齿轮参数和轴承支撑刚度分别如表1 和2 所示,时变啮合刚度和啮合误差如图7 所示。其中,啮合刚度和轴承支撑刚度采用ROMAX 软件在额定工况下计算得到,齿轮选用5 级精度。

表1 行星轮系齿轮参数Tab.1 Gear parameters in the planetary gear train

表2 轴承支撑刚度Tab.2 Bearing supporting stiffness
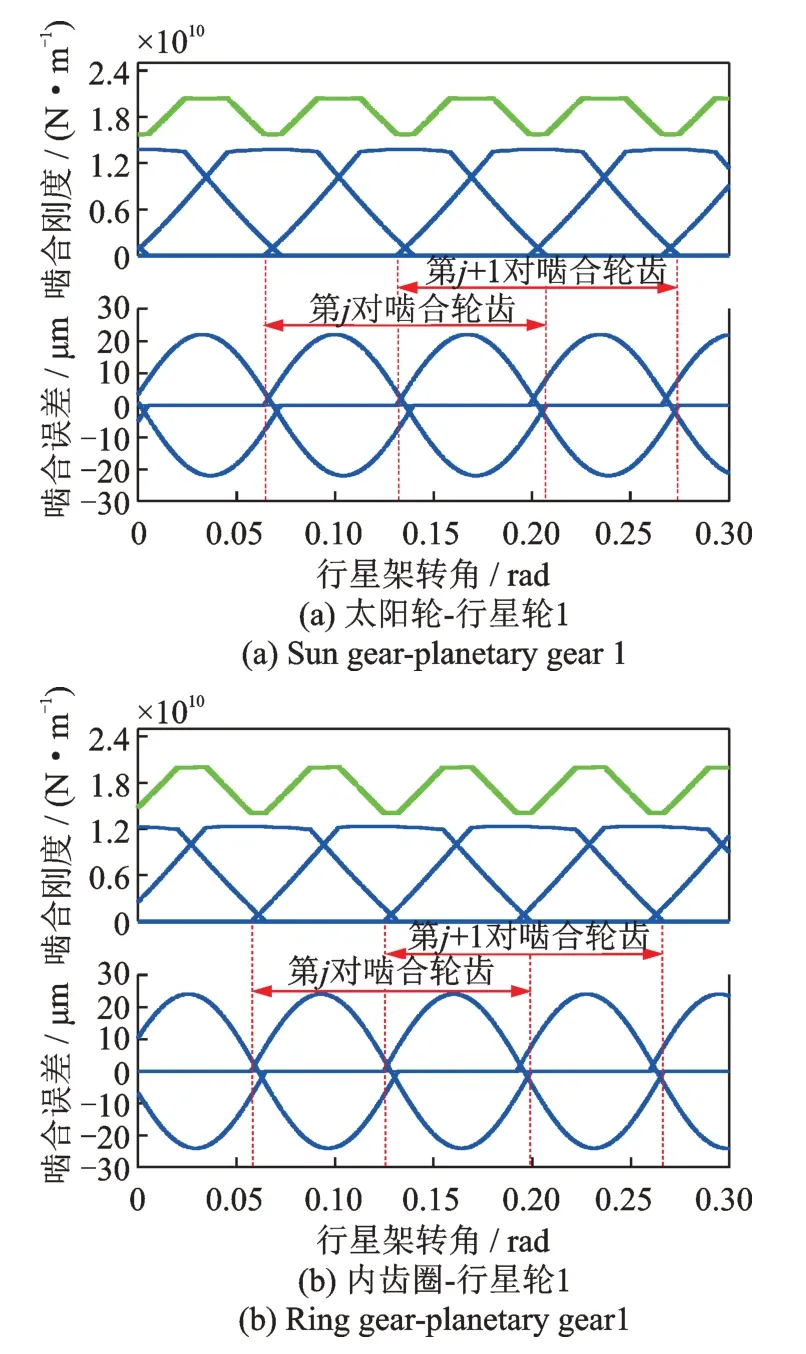
图7 时变啮合刚度和啮合误差Fig.7 Time-varying meshing stiffness and meshing error
2.1 模型验证
在额定工况下(Tin=4×106N⋅m),当行星架分别动态旋转至2π/10 rad 和2π/5 rad 时,行星轮、内齿圈和太阳轮的瞬态受力平衡位置如图8 所示,其中红色线表示变形后的状态,蓝色线表示原始状态。图9 所示为在行星架3D 有限元模型中,当A-A 处缩聚点固定时,在行星架销轴缩聚点施加顺时针(正视B-B 平面)切向力后行星架静态变形,模拟当行星架逆时针旋转时销轴缩聚点变形后的状态。
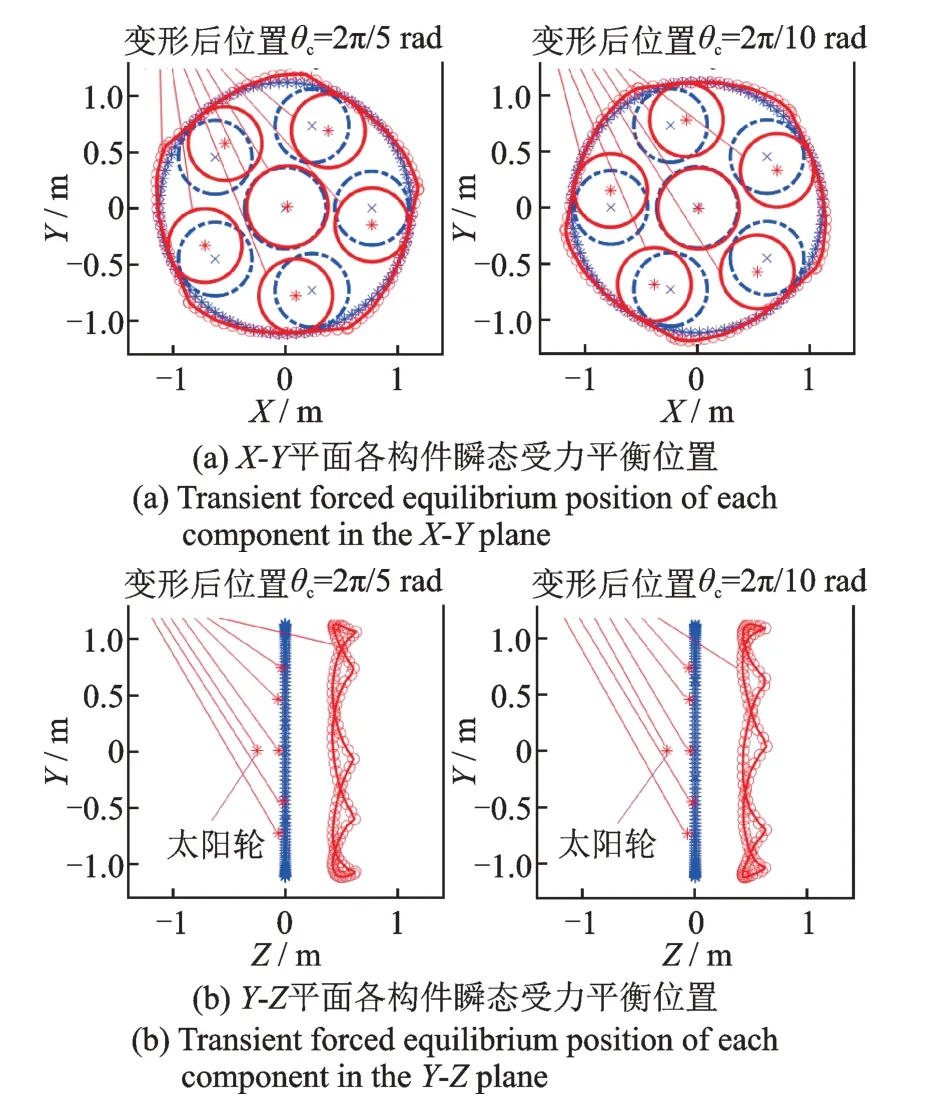
图8 行星轮系各构件瞬态受力平衡位置Fig.8 Transient forced equilibrium position of each component in the planetary gear train
从图8 中可知,行星轮切向位置变化与行星架旋转方向(逆时针旋转)相反,这与图9 所示的有限元模型销轴切向变形趋势较为吻合,其主要原因是由于行星轮主要传递周向力矩,造成行星轮沿切向的受力较大。此外,内齿圈轮齿节点的受力平衡位置整体呈“五角星”形状,且会随着行星架逆时针旋转。这是由于内齿圈同时与5 个行星轮啮合,导致内齿圈受挤压变形。太阳轮径向的受力平衡位置变化很小,其主要原因是由于行星轮径向对称布置,同时由于斜齿轮轴向分力相对于径向分力较小,内齿圈、行星架和太阳轮的轴向受力平衡位置变化较小。
2.2 啮合副变速表征变量
在恒定输入扭矩(Tin=4×106N⋅m)和扭矩突变工 况(Tin=4×106→2×106→4×106N ⋅m,Tin=4×106→0.2×106→4×106N⋅m)下,行星架转速变化如图10 所示,对应的恒定输入扭矩工况下内齿圈-行星轮啮合副变速表征变量(和)如图11 所示。从图10 中可知,当输入扭矩恒定时,初始阶段行星架转速逐渐增加,随后达到额定转速(输入转速11.27 r/min)并趋于稳定波动;当输入扭矩骤减时,行星架转速随之降低,而当扭矩恢复时,其逐渐增速至额定转速,同时还可以观察到扭矩跌落幅值越大,行星架转速波动也越大。从图11 中可知,随着行星架转角增大,内齿圈齿数序号逐渐增大,表明内齿圈轮齿依序参与啮合;并且由于多行星轮啮合存在相位差异,造成啮合副变速表征变量的初始位置沿内齿圈均匀分布。此外,啮合副变速表征变量曲线的两侧边缘出现了明显的周期性“毛刺”,这是由于内齿圈-行星轮啮合副重合度为非整数时造成的同时参与啮合的齿数周期性变化。
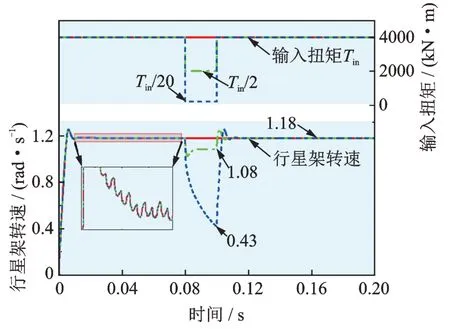
图10 行星架转速变化Fig.10 Changes of carrier rotation speed

图11 内齿圈-行星轮啮合副变速表征变量Fig.11 Characteristic variables for describing the variable speed process of meshing gear pairs of ring gear-planetary gear
为了进一步分析内齿圈轮齿啮合状态的变化规律,分别提取了内齿圈-行星轮1 啮合副载荷、内齿圈轮齿沿x向的振动位移,分别如图12 和13 所示。从图12 中可知,随着行星架转角增加大,内齿圈-行星轮1 同时参与啮合的齿数在2 和3 之间周期性波动,并且各轮齿动载荷先增大后减小,整体变化趋势与单对齿啮合刚度相似(如图7 所示)。从图13 中可知,随着行星架转角增加,内齿圈轮齿振动位移出现明显的循环波动,间隔相位为2π/5 rad,这是由于内齿圈同一轮齿先后与不同行星轮啮合;当行星架转角一定时,内齿圈所有轮齿振动位移整体呈原点对称分布,其主要原因是内齿圈轮齿动载荷方向(沿啮合线方向)与对应的局部坐标系之间的夹角会随着行星架转动而周期性变化。

图12 内齿圈-行星轮1 啮合副载荷Fig.12 Meshing gear pair loads of ring gear-planetary gear 1

图13 内齿圈轮齿节点沿x 向的振动位移Fig.13 Vibration displacements of ring gear tooth nodes in the x-direction
2.3 稳态工况
2.3.1 构件振动
当Tin=4×106N⋅m 时,太阳轮、行星轮和内齿圈振动位移分别如图14~16 所示。其中,全柔模型表示本文模型(式(22)),刚性模型则是将式(22)中太阳轮轴、内齿圈等构件视作刚体,但仍保留行星轮系多轮齿动态啮合关系。从图14~16 可知,考虑构件结构柔性后,太阳轮、行星轮和内齿圈振动位移幅值出现了不同程度增大。其中,内齿圈振动位移变化最为明显,呈现大幅低频波动(相邻行星轮相位与图13 相似)和高频振动(齿轮啮频)的叠加特征;内齿圈轮齿节点1 的最大振动位移峰值出现在y向,其次依次为x向和z向,分别为118.4,36.8 和12.5 μm,并且观察到x向振动位移峰值位置超前于y向和z向。其主要原因是随着行星架逆时针旋转,当行星轮与内齿圈轮齿节点1 刚好啮合时,沿着啮合线方向的轮齿动载荷在内齿圈轮齿节点1 处x向的投影量达最大,使得x向振动位移最早出现峰值;随着行星架转角继续增加,轮齿动载荷在y向的投影量逐渐增至最大值,随后出现振动位移峰值,并且在整个啮合过程中,轮齿动载荷沿y向的投影分量大于x向的投影分量。
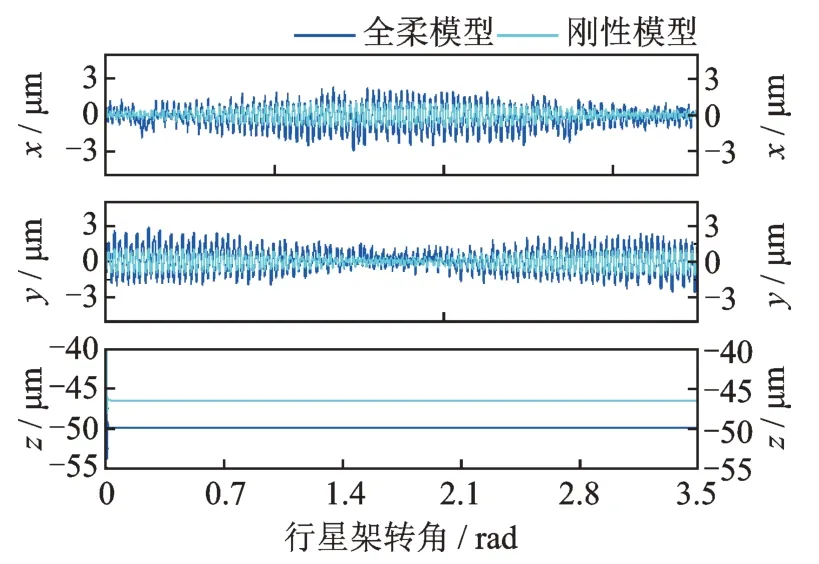
图14 太阳轮振动位移Fig.14 Vibration displacements of sun gear

图15 行星轮1 振动位移Fig.15 Vibration displacements of planetary gear 1

图16 内齿圈轮齿节点1 振动位移Fig.16 Vibration displacements of ring gear tooth node 1
2.3.2 轮齿载荷
图17 和18 分别为不同建模方式对太阳轮-行星轮1 和内齿圈-行星轮1 啮合副载荷的影响。其中,刚度分解表示根据啮合刚度幅值(如图7 所示),将全柔模型计算得到的动态啮合力分解到各轮齿上,进而得到轮齿动载荷,如下式所示:
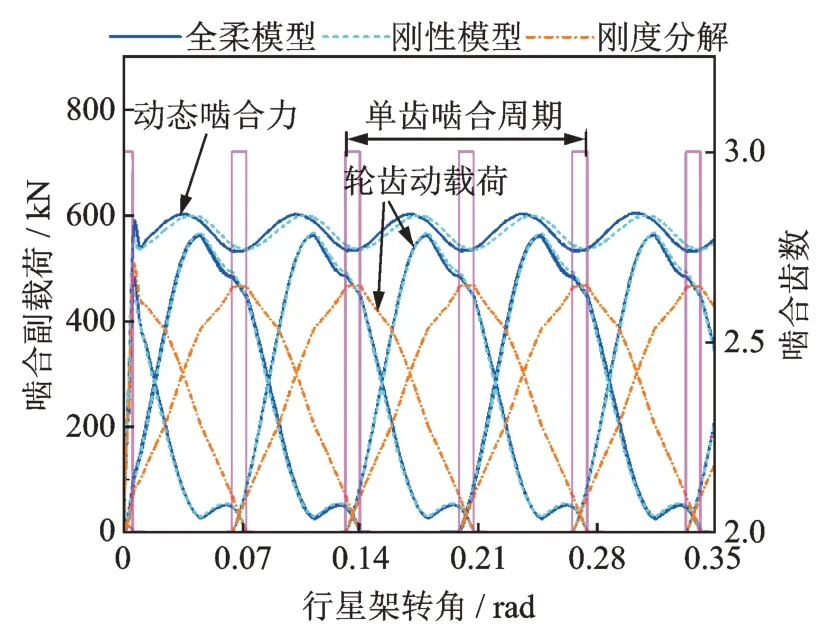
图17 太阳轮-行星轮1 啮合副载荷Fig.17 Meshing gear pair loads of sun gear-planetary gear 1

图18 内齿圈-行星轮1 啮合副载荷Fig.18 Meshing gear pair loads of ring gear-planetary gear 1
从图17,18 中可知,相较于刚度分解模式下的轮齿动载荷,考虑多轮齿动态啮合状态后,其轮齿动载荷峰值更大,且更偏向于左侧。因此若将动态啮合力直接按照啮合刚度幅值简单地分解到各轮齿上,容易低估轮齿动载荷幅值。在同一对内齿圈-行星轮i啮合副中,多轮齿啮合点沿啮合线方向等间隔分布,此时啮合点越靠近从动轮(内齿圈轮齿节点),内齿圈轮齿节点弹性变形在该处的投影分量将会越小(即式(4)中θrj叉乘系数更小),使得对应的啮合副相对位移更大,加之时变啮合刚度作用,造成相较于刚性模型,考虑构件柔性后,内齿圈-行星轮啮合副的轮齿动载荷峰值会朝左侧偏移(啮入起始点侧)。因此,考虑内齿圈结构柔性有助于获取更为准确的内齿圈-行星轮的齿轮动载荷分布。
2.3.3 均载系数
为了描述整个行星轮系因外载荷变动、构件变形、时变啮合刚度与传动误差等动态参数激励引起的均载性能变化,行星轮系均载系数的计算式为[31]:
计算结果如图19 所示。从图19 中可知,相较于刚性模型,考虑构件柔性后,行星轮均载系数增大。这是由于相较于全柔模型,刚性模型的内齿圈被简化为集中质量点,其振动位移幅值偏小(如图16 所示),且无法计算因轮齿动载荷造成的内齿圈局部挤压变形(如图8(a)所示),造成计算得到的内齿圈与5 个行星轮之间的动态啮合力较为理想。分析结果表明,若采用内齿圈-行星轮啮合副的动态啮合力计算行星轮均载系数(式(24)),建议在模型中考虑内齿圈结构柔性。
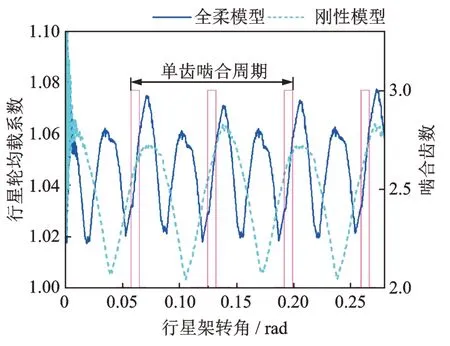
图19 行星轮均载系数Fig.19 Load-sharing coefficient of planetary gear
2.4 变速变载工况
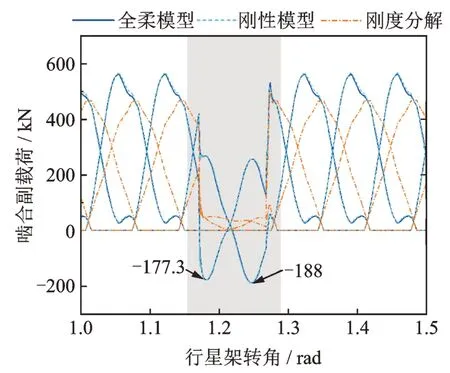
由于风速的随机性,风电齿轮箱需要在变速变载工况下长期运行。为了验证本文模型适用于变速变载工况,通过预设输入扭矩产生突变,获取构件振动位移、轮齿载荷以及均载系数。输入扭矩预设过程:①t≤1 s 时,Tin=4×106N‧m;② 1 s 2.4.1 构件振动 图20~22 分别为扭矩突变工况下太阳轮、行星轮和内齿圈的振动位移。从图20~22 中可知,当输入扭矩骤跌时,各构件的瞬态振动位移幅值明显降低;全柔模型和刚性模型均可以较好地计算太阳轮和行星轮的瞬态振动响应;相较于刚性模型,全柔模型可以计算得到更为详细的内齿圈轮齿节点瞬态振动响应,有助于指导内齿圈结构优化设计。 图20 太阳轮振动位移Fig.20 Vibration displacements of sun gear 图21 行星轮1 振动位移Fig.21 Vibration displacements of planetary gear 1 图22 内齿圈轮齿节点1 振动位移Fig.22 Vibration displacements of ring gear tooth node 1 2.4.2 轮齿载荷 图23 和24 分别为扭矩突变工况下太阳轮-行星轮1 和内齿圈-行星轮1 啮合副载荷的变化情况。从图23,24 可知,在全柔模型中,输入扭矩跌落会降低轮齿动载荷,且不同轮齿动载荷降幅存在差异,太阳轮-行星轮1 的轮齿动载荷分别降至-177.3 和-188 kN⋅m,内齿圈-行星轮1 的轮齿动载荷分别降至-202.5 和-110.8 kN⋅m,这意味对应的轮齿已发生脱齿,且容易产生反向接触。刚性模型计算得到的太阳轮-行星轮啮合副瞬态载荷变化与全柔模型计算结果差异较小;由于内齿圈结构柔性会吸收部分因冲击载荷引起的轮齿节点振动,造成刚性模型计算得到的内齿圈-行星轮啮合副中部分轮齿瞬态载荷略大于全柔模型计算结果。此外,相比于全柔模型计算结果,刚度分解模式下各轮齿动载荷均大于零,表明该方法不适用于计算变速变载工况下的轮齿动载荷。 图23 太阳轮-行星轮1 啮合副载荷Fig.23 Meshing gear pair loads of sun gear-planetary gear 1 图24 内齿圈-行星轮1 啮合副载荷Fig.24 Meshing gear pair loads of ring gear-planetary gear 1 2.4.3 均载系数 图25 所示为扭矩突变工况下行星轮均载系数的变化情况。从图25 可知,扭矩突变会显著增大行星轮均载系数,表明此时内齿圈与5 个行星轮之间的动态啮合力出现了明显差异。此外,由于柔性内齿圈的吸振作用,造成在扭矩突变期间内,柔性模型计算得到的行星轮均载系数明显小于刚性模型计算结果。因此,在计算变速变载工况下的行星轮均载系数时,建议考虑内齿圈结构柔性,可以提高计算结果精度。 图25 行星轮均载系数Fig.25 Load-sharing coefficient of planetary gear 本文将行星轮系啮合副常规等效单点啮合细化至多对轮齿啮合,通过引入啮合副变速表征变量和内齿圈虚拟振动线位移,构建了驱动轮转角与行星轮系多轮齿啮合状态的映射关系,并基于模态缩减理论,将内齿圈轮齿与弹性支撑进行耦合,建立计入结构柔性的风电齿轮箱行星轮系变速动力学模型,分析了工况变化对啮合副变速表征变量、构件振动、轮齿载荷和均载系数的影响,主要结论如下: (1)当5 个行星轮受力平衡时,行星轮切向变形量方向与行星架旋转方向相反;内齿圈轮齿节点瞬态变形整体呈“五角星”形状,且会随着行星架旋转;行星轮系各构件径向受力平衡位置变化最大,轴向受力平衡位置变化较小。 (2)在稳态工况下,内齿圈轮齿节点振动位移呈现大幅低频波动和高频振动的叠加特征;行星轮系轮齿动载荷先增大后减小,整体变化趋势与单对齿啮合刚度相似;轮齿动载荷会使柔性内齿圈产生局部挤压变形,影响均载性能。 (3)当输入扭矩跌落时,行星轮系各构件瞬态振动位移幅值将骤减;扭矩突变会破坏多个行星轮之间的动载荷平衡,恶化均载性能;柔性内齿圈可在一定程度上吸收部分因冲击载荷引起的构件振动,提高行星轮均载性能。 本文方法可以直接考虑传动构件复杂结构几何特征与多轮齿啮合状态,避免因简化处理带来的精度不足,为实现重载风电齿轮箱行星轮系变速动力学建模、提高动态特性分析精度提供了一种有效技术手段。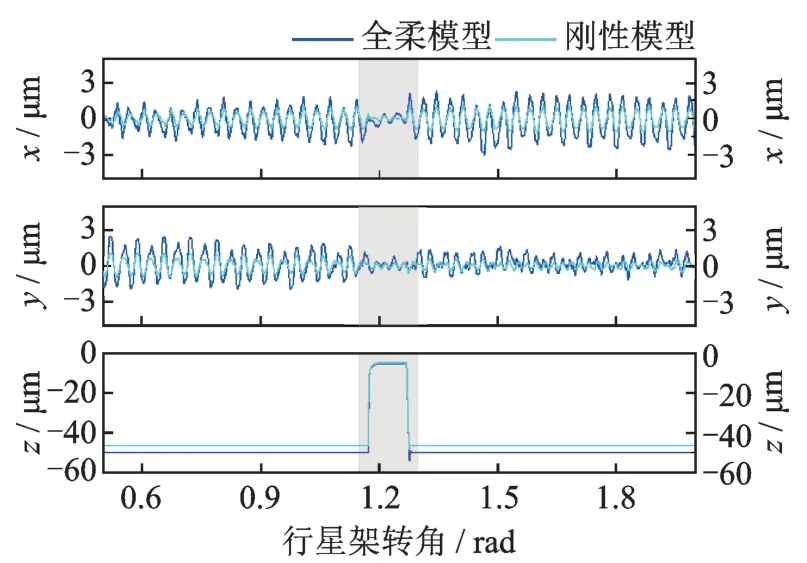




3 结论

