轮系传动比计算若干问题的探讨

侯莉侠，侯俊才，郭红利，张军昌

（西北农林科技大学 机械与电子工程学院，陕西 杨凌 712100）

0 引言

由一对齿轮所组成的机构是齿轮传动最简单的形式。但在机械传动中，为了获得很大的传动比或者为了将输入轴的一种转速变换为输出轴的多种转速，常将一系列互相啮合的齿轮的输入和输出轴连接起来，这种由一系列齿轮所组成的齿轮传动系统，称为轮系。［1］轮系传动比的计算不管是研究现有的传动系统还是设计新的传动系统都非常重要，笔者结合自己多年的经验，在此讨论几个关于轮系传动比计算过程中比较难懂的问题。

1 复合轮系中基本轮系的划分

复合轮系传动比的计算，首要问题就是如何正确地划分复合轮系中的基本轮系，也就是划分成单一的定轴轮系和单一的周转轮系，其中最关键的是找出基本的周转轮系。周转轮系是由行星轮、行星架、太阳轮和机架组成，所以应该先找行星轮，即找出那些几何轴线不固定而是绕其他轴线转动的齿轮。当行星轮找到后，那么支持行星轮的构件就是行星架，然后找与行星轮啮合的太阳轮，行星轮、太阳轮及行星架便组成一个周转轮系。去掉这个周转轮系后，复合轮系中可能还存在其他的周转轮系，找出所有的周转轮系后，剩下的就是定轴轮系。复合轮系中到底含有几个周转轮系，其判断标准是解决问题的关键。大多数《机械原理》教材明确指出根据行星架的数目来判断，［2，3］但是也有的教材“若有行星轮存在，同样可以找出与此行星轮相对应的基本周转轮系”。［4，5］这种说法很容易让初学者误解，认为轮系中有几个行星轮就对应几个基本的周转轮系。如图1所示的轮系，按照行星架的数目确定单一周转轮系时只有1个周转轮系；若按照行星轮的数目确定时就有2个基本的周转轮系，即构件1、2、2′、3、H组成一个周转轮系，构件4、5、6、H组成另外一个周转轮系。笔者认为按照行星架的数目确定基本周转轮系的方法更为合理。因为对于周转轮系传动比的计算大都采用转化机构法，即给整个周转轮系加一个反方向的行星架转速，让周转轮系转化为定轴轮系，然后按照定轴轮系传动比的计算方法来计算转化轮系的传动比。对于图1所示的轮系来说，只要加一个反方向的行星架转速，周转轮系就转化为定轴轮系，就可以按照定轴轮系传动比的计算方法列出如下方程，求解轮系中的传动比。

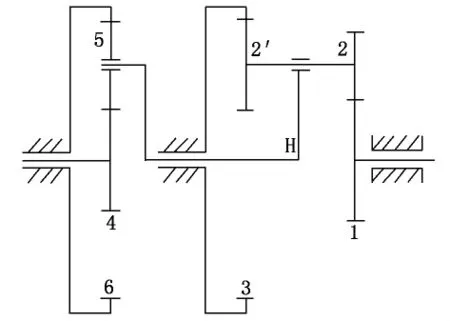
图1 复合轮系

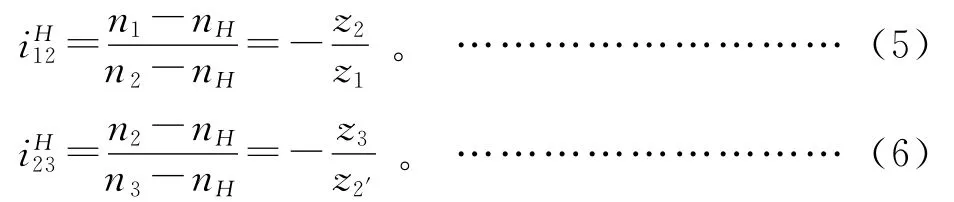
其中：ni为各轮转速；zi为各轮齿数。

23 K型周转轮系传动比的计算

3 K型周转轮系是由太阳轮、行星轮、行星架以及机架组成，其中有3个齿轮都是太阳轮，如图2所示。对于3 K型周转轮系传动比的计算有的参考书是把它分解成两个周转轮系，即构件1、2、2′、3、H 组成一个周转轮系，构件1、2、2″、4、H 组成一个周转轮系，然后分别列式子来计算轮系的传动比。［6］该做法很容易引起读者的误解，认为3 K型周转轮系是由两个周转轮系组成的。笔者认为既然3 K型周转轮系是一个周转轮系，即它只有一个行星架，在计算传动比的时候只需要给整个周转轮系加一个反方向的行星架转速，它就会成为定轴轮系。而转化机构法计算周转轮系的传动比时，iHAB中的A、B可以是周转轮系中的任意两个齿轮，可以是太阳轮，也可以是行星轮。因此针对3 K型周转轮系传动比的计算，可以选3个太阳轮中的1和3、3和4列两个传动比的计算方程式，然后联立求解计算传动比，而不是把3 K型周转轮系划分成两个周转轮系。

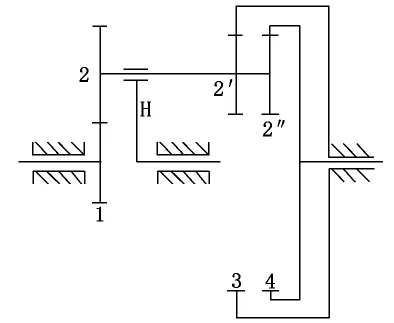
图2 3K型周转轮系

3 K型周转轮系转化成定轴轮系以后，可以列出3个方程式，取其中2个就可以求出结果。然而选择不同的2个方程式，计算过程的繁简程度不同。图2所示的周转轮系中，已知z1＝z2′＝19，z2＝57，z2″＝20，z3＝95，z4＝96，以 及 主 动 轮1 的 转 速n1＝1 920 r／min，求轮4转速的大小和方向。根据轮系转化法可以列出以下3个方程式：

代入各齿轮的齿数以及齿轮1的转速以后，由式（7）可得nH＝120 r／min；由式（8）可得77nH＝72n4＋9 600；由式（9）可得nH＝－24n4。显然通过方程式（7）和式（9）很容易求得n4＝－5 r／min。所以在选择方程式时一定要选转速为零的太阳轮和另外两个太阳轮分别列方程式，使计算过程尽可能简单。

3 双重系杆复合轮系传动比的计算

双重系杆复合轮系是一种较为复杂的组合轮系，其特点是主周转轮系的行星架内有一个副周转轮系，因此至少有1个行星轮同时绕着3条轴线转动。因为这种组合轮系包含了主、副两种周转轮系，所以称为双重系杆复合轮系。［7］双重系杆复合轮系传动比的计算方法有很多，这里只介绍便于初学者理解的机构转化法。通过二次转化把双重系杆复合轮系转化为周转轮系，然后再按周转轮系传动比的计算方法来计算。

在图3所示的轮系中，已知各轮均为标准齿轮，且模数相同，z1＝160，z2＝60，z2′＝20，z3＝40，z4＝100，z5＝20，z6＝80，z7＝120，求传动比i16。

在系杆4固定后，将此轮系视为由定轴轮系1、2，周转轮系2′、3、4、5及定轴轮系6、5、7组成的复合轮系，因此必须分别进行传动比计算，且只能对行星轮系2′、3、4、5再进行第二次转化。

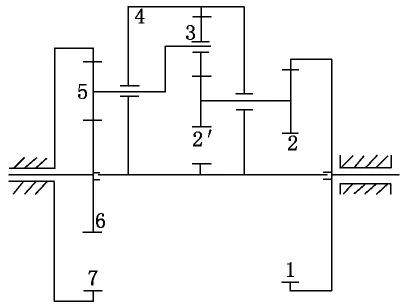
图3 双重系杆复合轮系

（1）齿轮1、2为定轴轮系，有：

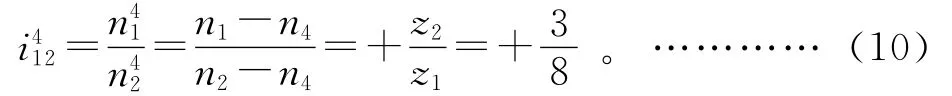
（2）齿轮2′、3、4及系杆5组成行星轮系，直接利用周转轮系的转化机构传动比公式或再对其轮系二次转化（即给此行星轮系以－n5绕系杆5轴线回转），有：

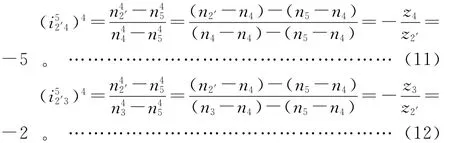
（3）齿轮6、5、7组成定轴轮系，有：

由于n7＝0，联立式（11）～式（14）计算得i16＝－5。

4 结束语

本文对复合轮系中基本轮系的划分、3K型周转轮系传动比的计算以及双重系杆复合轮系传动比的计算进行了分析、讨论，希望对传动系统的设计者能有所帮助。

［1］ 杨可桢，程光蕴，李仲生.机械设计基础［M］.北京：高等教育出版社，2006.

［2］ 孙恒，陈作模，葛文杰.机械原理［M］.北京：高等教育出版社，2006.

［3］ 邹慧君，傅祥志，张春林.机械原理［M］.北京：高等教育出版社，1999.

［4］ 王知行，刘延荣.机械原理［M］.北京：高等教育出版社，1999.

［5］ 张策.机械原理与机械设计（上册）［M］.北京：机械工业出版社，2004.

［6］ 杨家军.机械原理［M］.武汉：华中科技大学出版社，2009.

［7］ 黄锡恺，郑文纬.机械原理［M］.北京：高等教育出版社，1989.