轨道车辆牵引拉杆有限元分析

刘兴龙，陈一萍

（南车青岛四方机车车辆股份有限公司 高速列车系统集成国家工程实验室 （南方），山东 青岛 266111）

0 引言

牵引拉杆装置是轨道车辆中连接车体与转向架的一个重要部件，车体与转向架的纵向牵引力和制动力主要依靠牵引拉杆传递［1，2］；由于车辆在线路运行时会频繁地启动和制动，所以牵引拉杆需要承受多次往复循环载荷。为保证牵引拉杆使用的可靠性，本文采用有限元软件Hyper Mesh和ANSYS对该结构进行分析。

1 牵引拉杆组成结构模型

某型轨道车辆纵向牵引拉杆组成的CAD模型如图1所示。它由牵引拉杆和橡胶弹性节点组成，其中，弹性节点和牵引拉杆存在过盈装配关系。弹性节点结构从外向内由外套、橡胶和芯轴构成，橡胶与金属外套和芯轴通过硫化粘结在一起。

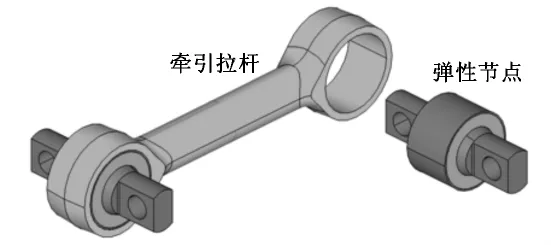
图1 牵引拉杆组成的CAD模型

2 有限元模型及分析

2.1 材料属性

橡胶材料采用Mooney－Rivlin本构模型，该本构模型适于模拟应变范围在30%～200%的橡胶材料的力学行为，其表达式为：

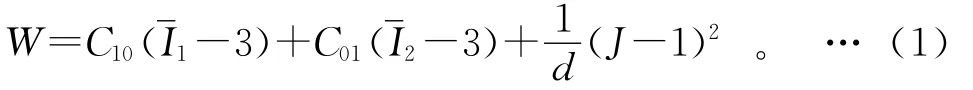
其中：W 为材料的变形能；I1和I2为应变偏量能；J为体积应变能；C10、C01、d均为材料参数。根据橡胶材料的硬度，计算中选取C01＝0.381，C10＝0.102，d＝0［3］。牵引拉杆和弹性节点的外套、芯轴材质均为合金钢，弹性模量E＝206 GPa，泊松比v＝0.3，屈服强度σs＝450 MPa，疲劳极限σ－1＝200 MPa。

2.2 网格划分

考虑到结构的对称性，取结构模型的1／4进行计算，以减小计算规模。首先利用Hyper Mesh有限元前处理软件对结构的几何模型进行处理并划分网格，然后利用ANSYS有限元软件进行求解分析，单元类型为一阶线性六面体单元Solid185。单元最小尺寸设定为3 mm，最大尺寸设定为6 mm，节点总数为21 882个，单元总数为18 928个，1／4牵引拉杆的有限元模型如图2所示。由于弹性节点不是本次分析的关注内容，因此将该部分的网格划分的疏一些，而对拉杆结构划分的相对密一些。采用通常的单元技术对诸如橡胶等不可压缩性材料进行计算分析时，会出现体积锁定问题［4］。为克服该问题，将Solid185单元设定为增强应变模式（又称为非协调模式），并采用混合位移－压力单元公式。

由于弹性节点与牵引拉杆之间的过盈接触关系直接影响着分析的准确合理性，因此在进行有限元建模时需要考虑它们之间的这种接触行为。在ANSYS中，可以在可能发生接触的实体单元表面建立一种表面单元来实现，建模时将拉杆的孔内表面定义为接触面，采用Conta173单元划分，弹性节点外套表面定义为目标面，采用Targe174划分。分析时忽略了拉杆与弹性节点的过盈配合接触关系，采用绑定（bonded）接触模拟他们之间的变形协调关系。载荷工况为对1／4模型的各对称面施加对称约束，对芯轴外伸端上表面施加沿X轴负向的疲劳载荷18.5 k N。

2.3 计算结果分析与验证

图3、图4分别为牵引拉杆组成的von Mises等效应力云图和沿X轴方向的位移ux变形云图。从图3可以看出von Mises等效应力最大值为209.6 MPa，发生在牵引拉杆的颈部，即杆头与杆身连接位置，低于材料的屈服极限450 MPa。需要指出的是，在弹性节点的芯轴与橡胶连接拐角部位，应力值也比较大，这是由于对该位置的过渡倒角进行了几何简化处理所导致的，在此不予考虑。从ux变形云图可知，最大位移量为7.3 mm，由此可知，牵引拉杆径向的等效刚度约为10.1 k N／mm。

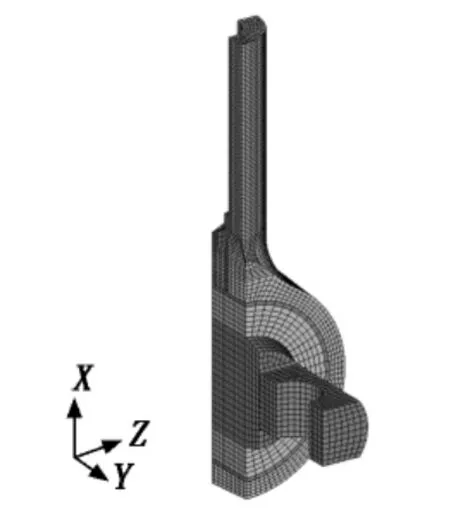
图2 牵引拉杆的有限元模型

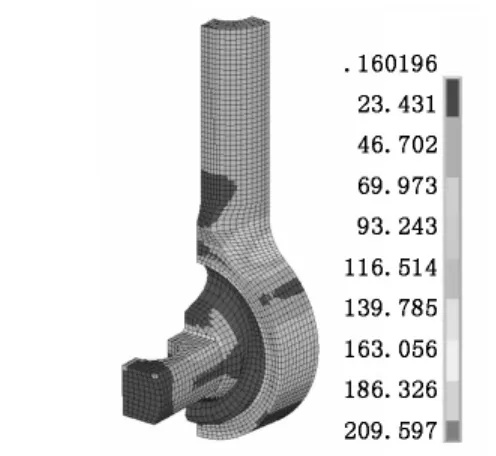
图3 牵引拉杆的等效应力云图

图5 、图6分别为牵引拉杆的第一主应力和第三主应力计算结果。第一主应力σ1的最大值为175.4 MPa，发生在牵引拉杆的颈部，第三主应力σ3的最大值为－86.6 MPa，发生在杆头外表面中间位置。根据第一主应力和第三主应力可以计算结构在疲劳载荷下的变应力幅值σa：

将上面的计算结果代入式（2）求得牵引拉杆的变应力幅值σa的最大值为88.93 MPa，发生在牵引拉杆的颈部。变应力幅值最大值低于材料的疲劳极限200 MPa，满足设计要求。

为了验证有限元分析的准确性，对牵引拉杆的变形和应力进行了实验测试，主应力测试位置如图7所示。实测最大变形量为10.0 mm（计算结果为7.3 mm），相对误差为27.0%，主应力测试与计算结果对比分析见表1。变形和应力的实验结果充分验证了有限元分析的准确合理性，计算与测试结果存在误差的原因一方面可能是由于橡胶材料的本构模型和参数值还不够准确，另一方面可能是实验中的测试误差造成的。

3 结论

本文对轨道车辆牵引拉杆结构进行了有限元分析，分析时考虑了橡胶材料的非线性和接触行为的非线性。计算结果表明，牵引拉杆装置在74.0 k N的拉伸载荷作用下，纵向变形为7.3 mm，径向等效刚度为10.1 k N／mm；第一主应力最大值为175.4 MPa，第三主应力最大值为－86.56 MPa，变应力幅值为88.93 MPa。实验测试结果充分验证了有限元分析的准确性。

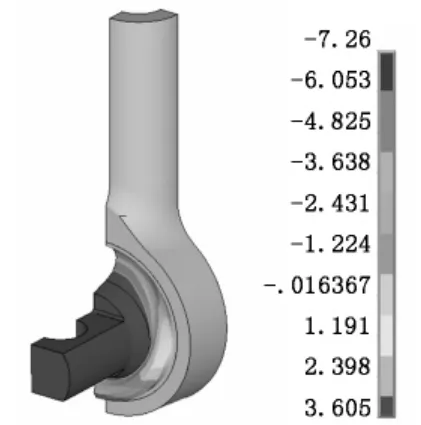
图4 牵引拉杆的u x变形云图

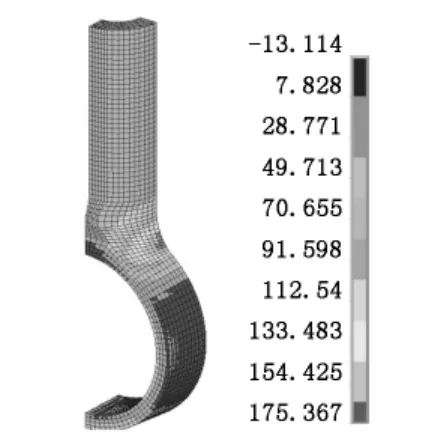
图5 牵引拉杆第一主应力云图

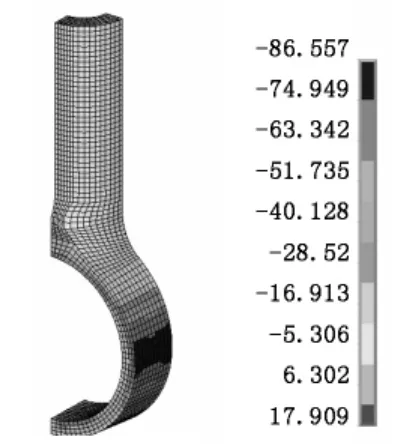
图6 牵引拉杆第三主应力云图

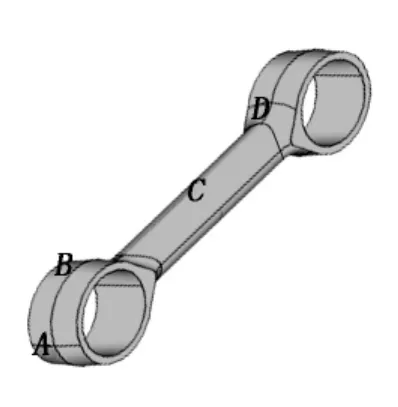
图7 主应力测试位置 示意图

表1 主应力测试和计算结果对比

［1］ 刘诚波.25T型客车用牵引拉杆节点故障原因分析及改进［J］.铁道车辆，2008，46（7）：14－15.

［2］ 吕一志.209T型转向架牵引拉杆装置的故障与改进［J］.铁道车辆，1998，36（5）：31－33.

［3］ 卜继玲，黄友剑.轨道车辆橡胶弹性元件设计计算方法［J］.北京：中国铁道出版社，2010.

［4］ Robert D Cook，David S Malkus，Miachel E Plesha，et al.有限元分析的概念与应用［M］.关正西，强洪夫，译.第4版.西安：西安交通大学出版社，2009.