基于改进火烈鸟搜索算法的移动机器人路径规划*

马 兵，吕彭民，刘永刚，韩红安，周 强，胡永涛

（1.长安大学道路施工技术与装备教育部重点实验室，陕西 西安 710064；2.河南卫华重型机械股份有限公司，河南 长垣 453400；3.河南工学院电气工程与自动化学院，河南 新乡 453003）

0 引 言

近年来，移动机器人最优路径规划是带有复杂约束的优化问题。然而，传统元启发式算法在求解机器人路径规划问题时，存在搜索效率低和寻优精度不高等不足之处。为弥补这些不足，研究学者从改善算法寻优性能的角度出发，提出了众多的改进算法。如：改进蚁群算法［1，2］，变步长蚁群算法［3］，多步长蚁群算法［4］，改进遗传算法［5］，改进果蝇算法［6］，改进灰狼优化算法［7］，改进粒子群优化算法［8］，改进正余弦算法［9］，烟花-蚁群混合算法［10］等。虽然，文献中已有算法可提高求解移动机器人路径规划问题的寻优效率和精度，但是，在复杂的地图环境下，仍存在局部搜索停滞和搜索效率低的问题。

受火烈鸟迁徙和觅食行为启发的火烈鸟搜索算法（flamingo search algorithm，FSA）是一种比较新颖的算法，与其他算法相比，FSA具有较好的稳定性和鲁棒性，可用于求解电路问题、路径规划、网络入侵预防系统等实际问题［11］。但对高维度复杂的问题时，仍存在易陷入局部最优、精度低、寻优效率低等问题，鉴于此，融合了自适应Sigmoid 非线性种群动态调整因子，混合精细分级搜索策略和逐维随机镜面反射学习策略，提出一种改进的FSA（improved FSA，IFSA），提高算法的搜索效率和求解精度，通过移动机器人路径规划问题，验证了所提出算法的有效性。

1 移动机器人路径规划环境建模

栅格化是移动机器人路径规划中通用的环境建模方法［12］。移动机器人路径规划环境可简化为由一定数量的相同栅格化区域组成，移动机器人等效为一个质点，可在每个栅格的中心点处自由移动。将移动机器人的运动空间由黑色栅格和白色栅格划分，黑色指障碍物栅格用1 表示。白色指无障碍物栅格用0 表示。按照从左至右，从上至下的划分顺序，将移动机器人运动空间划分为相同的栅格，并对每个栅格进行坐标编号。每个栅格的坐标（xi，yi）可由式（1）确定［1］

式中l为栅格的边长，mm为地图的维度。

2 IFSA

2.1 FSA

1）火烈鸟觅食行为

首先，火烈鸟利用鸟喙在一定范围内进行食物扫描，易发现更多的食物；其次，发现食物较多的火烈鸟，通过与其余火烈鸟之间的交流来指引火烈鸟不断向食物多的地方移动；最后，通过部分火烈鸟靠双足不断移动到食物丰富的区域。这种觅食行为可用式（2）来描述

式中和分别为火烈鸟在第k+1 次和第k次迭代时在种群中第j维中的觅食位置为火烈鸟的当前最优觅食位置，ζ1和ζ2为-1或者1 的随机数，α1和α2均服从标准正态分布，C为随机扩散系数，其服从自由度n的卡方分布。

2）火烈鸟迁徙行为

当觅食区域食物匮乏时，火烈鸟群体会利用双足整体迁徙到其他区域，继续寻找更多的食物。这种迁徙行为可用式（3）来描述

式中和分别为火烈鸟在第k+1次和第k次迭代时在种群中第j维中的鸟脚位置为种群中第j维的火烈鸟当前最优位置，β为服从自由度n的高斯随机数。

FSA算法步骤如下：1）火烈鸟种群初始化，定义算法初始参数，种群数量N，最大迭代次数kmax，第1部分迁徙火烈鸟比例为MPb。2）评估适应度函数的值，确定最优火烈鸟位置和适应度值。3）更新参与觅食的火烈鸟的数量MPr＝rand［0，1］×N×（1 -MPb）及参与第2部分迁徙的火烈鸟数量MPt＝N×（1 -MPb）-MPr。4）根据式（3）更新火烈鸟的迁徙位置和式（2）更新火烈鸟的觅食位置。5）判断是否达到最大迭代次数，若是，则转到步骤（6）；否则，返回步骤（2）继续寻优。6）输出火烈鸟最优位置和最优适应度值。

2.2 IFSA

1）自适应Sigmoid种群比例因子策略

FSA中，迁徙火烈鸟种群比例因子MPb是固定值，且觅食火烈鸟种群受MPb影响，这就容易导致在迭代搜索过程中，算法的种群自我调整能力较低，使得算法寻优能力弱。因此，引入Sigmoid函数对MPb进行非线性处理，如式（4）

式中MPb0为迁徙火烈鸟种群初始比例因子。

在整个迭代过程中，种群比例因子变化情况，如图1 所示。由图1可知，随着迭代次数增加，一方面，种群比例因子MPb，MPr和MPt呈现非线性变化。另一方面，MPb和MPt之间的产异性ΔD1逐渐增大，这有利于算法的全局搜索，同时MPr和MPt之间的产异性ΔD2也随之逐渐增大，这有利于算法的局部搜索。这就说明了自适应Sigmoid 种群比例因子策略有利于平衡算法的全局搜索与局部搜索，提高算法的寻优能力。

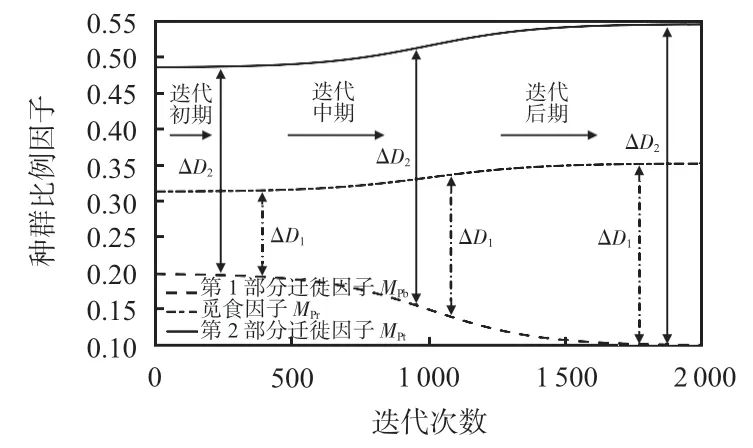
图1 种群比例因子变化

2）自适应混合精细分级搜索策略

在火烈鸟觅食过程中，食物源的分布不均性影响着火烈鸟种群的移动。当引导觅食的火烈鸟获得的食物源处于局部最优附近邻域时，其余的火烈鸟会移动且聚集处于停滞状态。这样会导致种群位置的多样性降低，增加了算法陷入局部极值的可能性。鉴于此，将觅食过程根据迭代次数划分为3 个阶段，采用自适应混合精细分级搜索策略：第1阶段：当k＜kmax／4 时，采用原有的觅食搜索方式；第2阶段：当kmax／4≤k≤3kmax／4 时，利用正余弦振荡特性［13］，引入自适应精英引导正余弦搜索方式，这样有利于增加种群多样性提高算法局部搜索能力；第3 阶段：当3kmax／4 ＜k≤kmax时，利用黄金分割方式，不断地细化搜索空间，引入用黄金正弦搜索方式［14］，丰富算法的搜索空间，进一步平衡算法的“搜索”与“开发”提高算法全局寻优能力。因此，整个觅食过程火烈鸟的位置更新可按式（5）进行

式中r1为［0，2π］内随机数，r2为［0，π］内随机数，r3为服从高斯分布的随机数。φ为自适应非线性调整因子取值范围为［0，1］，可由式（6）计算

3）逐维随机镜面反射学习策略

a.随机镜面反射学习策略

传统的镜面反射学习（specular reflection learning，SRL）策略如图2，为增加算法寻优过程中，个体A0（即当前解X）沿入射线A经过镜面的反射，沿反射线B产生个体B0（即反向解X*），根据点X产生当前解和X*产生的反向解之间择优选择进入下一次迭代［15］。

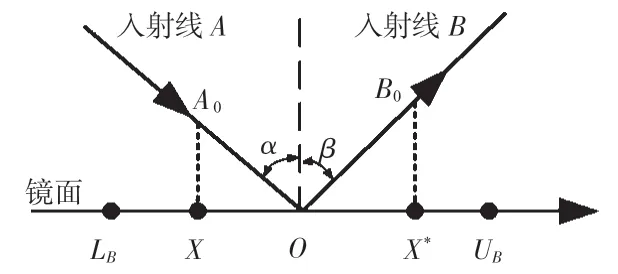
图2 传统SRL模型

根据SRL模型，由X产生的反向解X*可用式（7）表示

式中λ为反射影响系数，可由式（8）定义

式中ξ，R0，κ1和κ2均为［0，1］内的随机数。

虽然，在算法寻优过程中，SRL策略可以丰富种群多样性。但是，对于复杂高维问题，SRL 的随机性较弱，无法有效地增强搜索空间内的种群多样性。为进一步增强种群多样性，提高算法的收敛速度和求解精度。本文提出一种随机SRL（random SRL，RSRL）策略，如图3所示。由点产生一个随机反向解替代点B0原有反向解，这样可以增强SRL的随机性，增强种群跳出局部极值的能力。因此，在RSRL中，由式（9）替代式（7）

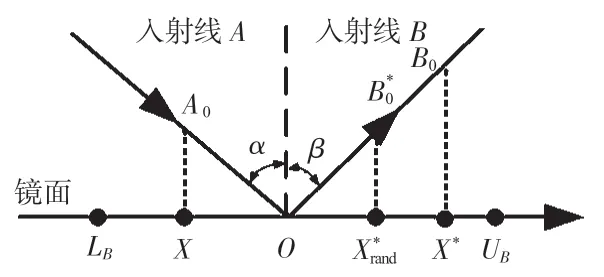
图3 RSRL模型

式中η为服从高斯分布的［0，1］内的随机数。

b.逐维RSRL策略

FSA中，火烈鸟种群位置更新过程中，各维度之间存在互相干扰，影响算法的收敛精度与速度。为此，在火烈鸟种群更新后，引入逐维RSRL策略，增加各维度之间的信息交流，以保留精英方式进行逐维RSRL，丰富种群搜索空间，增强种群多样性，降低了保证算法的收敛效率和寻优精度。火烈鸟位置更新参照式（10）

式中为种群在j维数上的反向解，UB（j）和LB（j）为种群在j维上的上下限为种群在j维数上的当前解。

2.3 基于IFSA的移动机器人路径规划

具体步骤如下：1）采用栅格化法构建地图，初始化机器人起始点和终点，设置算法的初始参数。2）初始化火烈鸟种群的位置及评估适应度函数值确定初始最优位置。3）按照式（4）和式（6）分别更新MPb和φ。4）按照式（3）更新火烈鸟的迁徙位置。5）按照式（5）分段更新火烈鸟的觅食位置。6）按照式（7）～式（10）对火烈鸟的位置进行学习。7）重新评估适应度值，更新最优火烈鸟位置和适应度值。8）是否达到最大迭代次数，若是则输出最优路径，否则返回步骤（3）继续寻优。

3 路径规划实验仿真

分别选择FSA［11］、灰狼优化（GWO）算法［16］、正余弦算法（SCA）［13］和IFSA 应用于移动机器人路径规划问题中。算法的最大迭代次数设置为1 000，独立运行次数为30。选取3种不同大小的栅格化地图（即20 m×20 m，30 m×30 m，40 m×40 m）。图4给出不同算法在不同地图中的最优路径和迭代收敛曲线，表1为实验仿真统计结果。

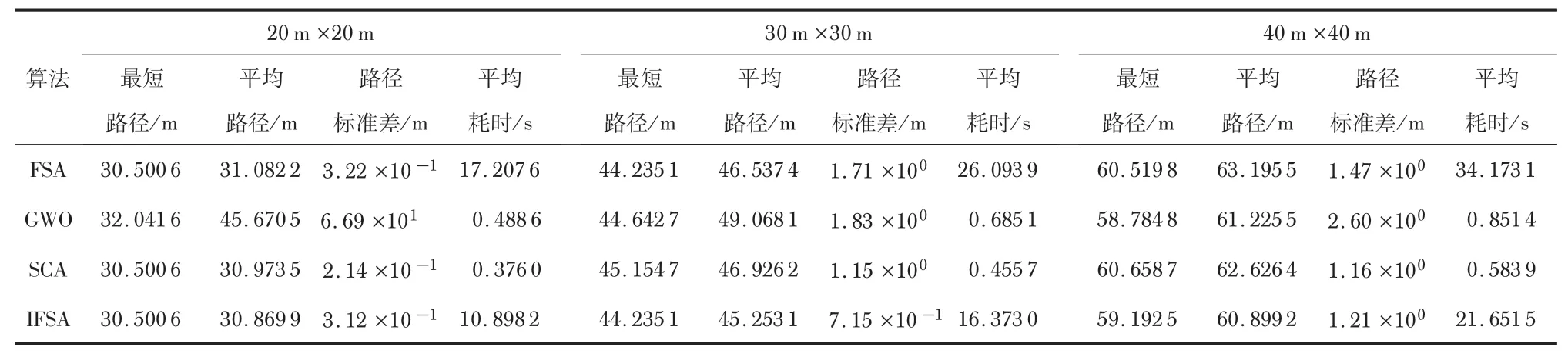
表1 4 种算法在不同地图中的路径规划结果

从最短路径长度来看，由表1 结果可知，对于20 m ×20 m的栅格地图，IFSA，SCA和FSA可获得最小路径长度为30.500 6 m，其结果优于GWO 算法。对于30 m ×30 m 的栅格地图，IFSA和FSA寻优可得最小路径为44.235 1 m，明显优于GWO和SCA。对于40 m ×40 m 的栅格地图，GWO 算法拥有最小的路径长度为58.784 8 m，但是IFSA 的最小路径长度优于FSA 和SCA。因此，对于复杂的地图环境下，IFSA可提供较好的最优路径长度结果。这表明了IFSA 具有较好的寻优能力。

从平均路径和路径标准差来看，由表1 结果可知，对3 种地图环境，与SCA，FSA 和GWO 算法相比，IFSA 可以提供较小的平均路径长度。对于20 m ×20 m 和40 m ×40 m的栅格地图，IFSA路径标准差劣于SCA 算法，但优于FSA和GWO。这些结果表明，IFSA 具有较好的稳定性和鲁棒性。

从收敛曲线和路径最优规划路线来看，由图4 可知，FSA迭代前期存在严重的停滞现象，但与其他算法相比，IFSA可以以较少迭代次数和转弯次数获取最优的移动机器人路径规划方案。

4 结 论

本文融合了自适应Sigmoid非线性种群动态调整因子，混合精细分级搜索策略和逐维RSRL 策略，提高了IFSA 的寻优精度和搜索效率，克服了FSA 在解决移动机器人路径规划时存在易陷入早熟的问题。与其他算法相比，对于复杂的路径规划问题，IFSA体现出了较好的实际适用性。