围长给定双圈图的Aα-谱半径的上界

叶蔼云

1.青海师范大学 数学与统计学院，青海 西宁 810008；2.盐城师范学院 数学与统计学院，江苏 盐城 224002

设G=(V(G)，E(G))为n阶简单无向图，顶点集V(G) ={v1，v2，…，vn}（n∈ℕ），边集E(G) ={e1，e2，…，em}(m∈ℕ)，记图G的邻接矩阵和度对角矩阵分别为A(G)、D(G)，定义图G的无符号拉普拉斯矩阵Q(G) =D(G) +A(G)，称矩阵A(G)、Q(G)的最大特征值分别为图的谱半径和无符号拉普拉斯谱半径。2017年，Nikiforov［1］定义图G的Aα-矩阵为

图G的Aα-矩阵可以看作是图G的邻接矩阵和无符号拉普拉斯矩阵的共同推广，其最大特征值称为图G的Aα-谱半径，记作ρα(G)。

图的Aα-矩阵的概念一经提出就迅速引起了国内外学者的关注，其中最受学者关注的问题是：对给定的图类寻求其Aα-谱半径的界并且刻画达到界的极图，这也是Brualdi-Solheid 问题在Aα-矩阵上的推广。2017 年，Nikiforov 等［2］给出最大度给定的树的Aα-谱半径一个紧的上界；2018年，Nikiforov 等［3］和Xue 等［4］同时确定了直径给定图的Aα-谱半径最大的图和团数给定图的Aα-谱半径最小的图；同年，Lin 等［5］分别确定了顶点数和割点数给定图的Aα-谱半径最大的图，顶点数和匹配数给定树的Aα-谱半径最大的图；2021 年，Li 等［6］分别刻画了时，边数给定、团数和边数给定以及色数和边数给定图的最大Aα-谱半径的极图。

双圈图是边数等于顶点数加1 的简单连通图，图G的围长是指G中最短圈的圈长，Wang等［7］确定了围长为g的n阶双圈图的谱半径的上界和极图；Li 等［8］和Zhu［9］分别独立确定了围长为g的n阶双圈图的无符号拉普拉斯谱半径点数的上界和极图。本文确定了时，围长为g的n阶双圈图Aα-谱半径的上界和极图，推广已有的成果。

1 记号与引理

用Cn表示n个顶点的圈、Pn表示n个顶点的路、Sn表示n个顶点的星图，对于图G，dG(vi)表示顶点vi的度，N(vi)表示顶点vi的邻接点集，图G-uv为从G中删去边uv∈E(G)所得的图，G+uv为在G中添加一条边uv（u，v∈V(G)，uv∉E(G)）所得的图。图G的悬挂顶点是指度为1 的顶点，悬挂边是指与悬挂顶点相关联的边。若G为连通图，则Aα(G)是不可约的，根据非负矩阵的Perron-Frobenius 定理，ρα(G)的重数为1，并且存在唯一的正单位特征向量X=(x1，x2，…，xn)T，此向量称为Aα(G)的Perron向量。

设Cz、Ct是两个顶点不相交的圈（z、t是正整数，且z、t≥3，分别表示Cz、Ct的圈长。不失一般性，假定z≥t），v1是Cz的一个顶点，vl是Ct的一个顶点，B1(z，l，t)表示Cz、Ct通过长为l- 1(l≥1)的路v1v2…vl连接而成的图（见图1，当l= 1 时，图1中的v1、vl将粘合成一点）。设Pp+1、Pq+1、Pr+1是3个顶点不相交的路（p、q、r是正整数，分别表示Pp+1、Pq+1、Pr+1的路长，且至多有一条路的长为1，因此假定r≥q≥p≥1），B2(p，q，r)表示将这3 条路的始点和终点粘合而得到的图（图2）。

图1 B1(z，l，t)Fig. 1 B1(z，l，t)

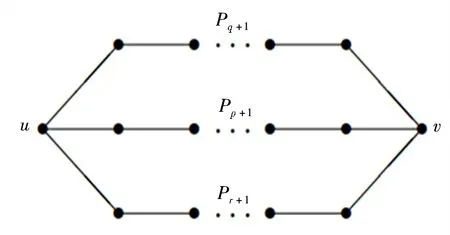
图2 B2(p，q，r)Fig. 2 B2(p，q，r)

在B1(z，l，t)、B2(p，q，r)的某些顶点接出一些树形成的双圈图，分别称为第一类双圈图和第二类双圈图，同时称B1(z，l，t)、B2(p，q，r)为双圈图的基图，并用B(n，g)表示所有围长为g的n阶双圈图所构成的集合，B1(n，g)表示第一类型中围长为g的n阶双圈图所构成的集合，B2(n，g)表示第二类型中围长为g的n阶双圈图所构成的集合，B1*(z，l，t)表示在B1(z，l，t)的4 度顶点上接出一些悬挂边所得的n阶双圈图，B2*(p，q，r)表示在B2(p，q，r)的某个3 度顶点上接出一些悬挂边所得的n阶双圈图，B22*(p，q，r)表示在B2(p，q，r)的某个2 度顶点上接出一些悬挂边所得的n阶双圈图。

引理1［2-3］设α∈[0，1) ，G为连通图，u、w是G的两个顶点，uvi∈E(G) 且wvi∉E(G)(i=1，2，…，k，k≤n)，X=(x1，x2，…，xn)T为对应ρα(G)的Perron向量，G′为从G中删除边uvi并加上边wvi得到的图。若xw≥xu，则ρα(G) ＜ρα(G′)。

由引理1容易得到下面的推论。

推论1设e=uv是连通图G的非悬挂边，N(u) ∩N(v) = ∅，在G-uv中粘合顶点u和v，得到的新顶点仍记为顶点u，在u点接出一条悬挂边所得到的图记为G′，若α∈[0，1) ，则ρα(G) ＜ρα(G′)。

引理2［1］设G为n阶图，其最大度为Δ，若，则ρα(G) ≥αΔ+，当且仅当且G=Sn时等式成立。

引理3［1］设G是没有孤立顶点的通图，若α∈[0，1) ，则

引理4设，n≥2g- 1，则

下面分两种情形证明引理4。

情形1：g= 3。

证明：g= 3 时，根据n≥2g- 1，n取最小值5。

根据对称性，不妨设x2≥x4，则

根据引理1，得到

情形2：g≥4。

证明：令h=n- 2g+ 1，根据引理3，可得

根据引理2，可得

由于n≥2g- 1，g≥4，不难验证

从而

2 主要结果

通过研究围长为g的n阶双圈图的Aα-谱半径，可以证明如下定理。

定理1设α∈[0，1) ，G∈B1(n，g)，则ρα(G) ≤，当且仅当时等号成立。

证明：由于G∈B1(n，g)，设G为B1(n，g)中Aα-谱半径最大的图，B1(p，1，q)为G的基图，则q=g、p≥g、l≥1。

设X=(x1，x2，…，xn)T是Aα(G)的Perron 向量（xi对应顶点vi，i= 1，2，…，n），v1v2…vl为G中连接圈Cp和Cq的路，假设l≥2，并对边v1v2应用推论1，可得图G′∈B1(n，g)使得ρα(G) ＜ρα(G′)，这与假设G为B1(n，g)中Aα-谱半径最大的图矛盾。因此，l= 1，即V(Cp) ∩V(Cq) ={v1}。

设G中的圈Cp=v1v2…vpv1，假设p≥g+ 1，并对边v1v2应用推论1，可得图G′∈B1(n，g)使得ρα(G) ＜ρα(G′)，这与假设G为B1(n，g)中Aα-谱半径最大的图矛盾。因此，p=g，即G是在B1(g，1，g)的某些顶点处接出树所得到的图。

现在证明G中在B1(g，1，g)上接出的树都是星。假设在B1(g，1，g)的某个顶点vi处接出的树Ti不是星，则Ti中存在非悬挂边vivj；对边vivj应用推论1，可得G′∈B1(n，g)使得ρα(G) ＜ρα(G′)，这与假设G为B1(n，g)中Aα-谱半径最大的图矛盾。因此，G中在B1(g，1，g)上接出树都是星。

现在证明G是在B1(g，1，g)的顶点v1处接出星所得到的图。假设在B1(g，1，g)的两个顶点vi、vj上分别接出星Si和Sj，不妨设xi≥xj，令

不难看出G′∈B1(n，g)，由引理1 可知ρα(G) ＜ρα(G′)，这与假设G为B1(n，g)中Aα-谱半径最大的图矛盾。因此，G是在B1(g，1，g)的某一个顶点vi上接出星所得到的图。

现在证明G是在B1(g，1，g)的顶点v1处接出星所得到的图。若i≠1，对顶点v1和vi应用引理1，可得，这与假设G为B1(n，g)中Aα-谱半径最大的图矛盾。因此，G是在B1(g，1，g)的顶点v1处接出星所得到的图。

定理2设1，则，当且仅当时等号成立。

证明：由于G∈B2(n，g)，设G为B2(n，g)中Aα-谱半径最大的图，B2(p，q，r)为G的基图，其中1 ≤p≤q≤r，则p+q=g。

设X=(x1，x2，…，xn)T是Aα(G) 的Perron 向量，其中xi对应顶点vi，i= 1，2，…，n。假设r≥q+ 1，因为p至少为1，且q不为1，所以q≥2，故r≥3。设Pr+1( =u) =v1v2…vr+1( =v)，对边v1v2运用推论1，可得图G′∈B2(n，g)使得ρα(G) ＜ρα(G′)，这与假设G为B2(n，g)中Aα-谱半径最大的图矛盾。因此，r=q，G是在B2(p，q，q)的某些顶点处接出树所得到的图。

现在证明G是B2(p，q，q)或G是在B2(p，q，q)的某一顶点vi处接出一些悬挂边所得到的图。

假设G=B2*2(p，q，q)，分两种情形讨论。

情形1：q-p≤1。

由于p+q=g，故，又r=q，故G=。 设，因，则y≥2，G是在的某个2度点处接出y条悬挂边所得到的图。

由引理2可得

再由引理3，可得

情形2：q-p≥2。

由于p+q=g，故，又r=q，故。 设z=n-p- 2q+ 1，因n≥，故z≥1，G是在B2(p，q，q)的某个2 度点处接出z条悬挂边所得的图。

由引理2可得

再由引理3，可得

由于p+q=g、q≥+ 1，从而

当z取最大值时，

从而

这与假设G为B2(n，g)中Aα-谱半径最大的图矛盾。

综合情形1、情形2，可以得到G=B2(p，q，q)或(p，q，q)。

现在证明q-p≤1时，

假设q-p≥2，则G=B2(p，q，q)或G是在B2(p，q，q)的某个3 度点处接出一些悬挂边所得到的图。这里双圈图G的基图顶点数为g+q- 1，若G=B2(p，q，q)，图G是没有悬挂点且顶点n=g+q- 1，则z=n-p- 2q+ 1 =n-g-q+ 1 = 0；若G是在B2(p，q，q)的某个3 度点处接出一些悬挂边所得的图，为了保证有悬挂点，图G的顶点数n≥g+q，则z=n-p- 2q+1 =n-g-q+ 1 ≥1。

综合以上讨论z≥0。

由引理2可得

再由引理3，可得

当z取最大值时，

从而

这与假设G为B2(n，g)中Aα-谱半径最大的图矛盾。因此，q-p≤1。

定理3G是围长为g的n阶双圈图，设，则

由于B(n，g) =B1(n，g) ∪B2(n，g)，由引理4和定理1、定理2容易得到定理3的结论。