预制T梁的水化热效应及温度应力影响因素研究

唐 杨

（五峰土家族自治县农村公路管理所，湖北 宜昌 443413）

混凝土结构在养护过程中由于内外温差、外部约束等原因，容易产生较大主拉应力，当主拉应力超过混凝土抗拉强度时，混凝土构件将出现开裂，极大地影响结构的承载能力和使用功能。

混凝土构件中，T 梁构件使用得比较普遍，因此关于T梁构件的水化热研究在工程实践中显得尤为重要。文献［1-2］基于宁夏某梁场进行水化热试验，并采用MIDAS 有限元分析软件进行仿真模拟，结果表明T 梁构件的梁端位置存在较大的开裂风险，通过优化T梁的配合比设计，可以降低水化热带来的不利影响；郝文彬［3］以蒲都高速某T 梁桥为工程背景，对预制T 梁早期开裂机理进行分析，发现温度应力是预制T 梁出现早期裂缝的根本原因，建议底模采用钢模以减少外部约束，同时使用钢纤维或者聚丙烯纤维增强抗裂能力，并设置草布等温控措施；姜增国等［4］对湖北高速公路某一榀跨径40 m 的T 梁进行数值分析，发现浇筑温差和混凝土自身水化热造成的温度应力是T 梁出现裂缝的主要原因；唐忠林等［5］以云南楚姚高速公路云山特大桥40 m 预制混凝土T梁为例，通过有限元分析同样得到了温度应力是造成T 梁开裂的主要原因，同时混凝土均质性较差造成收缩应力的叠加，加重了T梁的开裂风险；何舒法等［6］采用ADINA 软件对T梁进行水化热分析，得到水化热温度在7～9 h 达到峰值、温度应力小于混凝土抗拉强度的结论。

本文以某T 梁桥新建项目为工程背景，对预制T 梁的水化热效应进行仿真分析，同时通过改变混凝土原料配比和环境温度等因素，研究其对预制T梁水化热效应的影响。

1 工程概况

湖北省五峰土家族自治县湾潭镇某新建T梁桥的跨径组合为2×25 m，每跨包含4 片T 梁，T 梁采用C50 混凝土，为装配式预应力混凝土结构。本文选取预制T 梁的中梁进行分析，中梁的具体结构尺寸如图1所示。

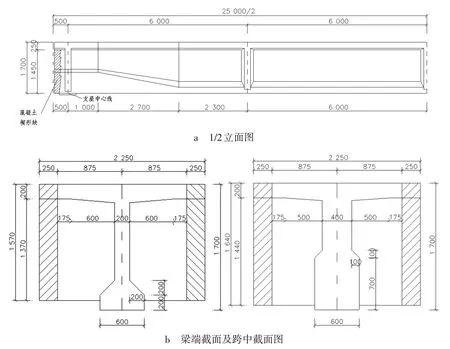
图1 预制中梁结构尺寸 单位：mmFig. 1 Structure size of prefabricated middle beam

T 梁的中梁长24.92 m，其中跨中截面段长16.6 m，渐变段长2×2.7 m，梁端截面长2×1.46 m；中梁高1.7 m，横隔板厚0.2 m。每片预制中梁的顶板宽1.75 m，厚0.2 m；梁端截面的肋板宽0.4 m，跨中截面的肋板宽0.2 m，在肋板马蹄部位增大到0.6 m；梁端截面的马蹄部位高0.8 m，跨中截面的马蹄部位高0.4 m；梁端截面与跨中截面存在2.7 m 长的线性过渡段，每片T 梁之间的湿接缝宽0.5 m，即图1b中阴影部分。

2 理论分析

2.1 热传导微分方程

混凝土结构在实际工作条件下的热传导微分方程为［7］

式中：T为温度场，表示温度在时间域和空间域的分布，℃；t为混凝土结构龄期，h；λ 为混凝土的导热系数，kJ/（m·h·℃）；cp为混凝土的质量定压热容，kJ/（kg·℃）；ρ为混凝土的密度，kg/m3；θ为混凝土的绝热温升，℃；x、y、z分别为空间域的3 个坐标轴。

2.2 初始条件

初始时刻的温度场可以视为一个常量，初始条件为

式中C为常量。

2.3 边界条件

边界条件通常有4 类［7］，其中第一类边界条件为边界温度是龄期t的函数，即

式中：t为混凝土龄期，h。

第二类边界条件为混凝土结构表面的热流量是龄期t的函数，即

式中：n为表面外法线方向；t为混凝土龄期，h。

第三类边界条件为已知混凝土结构表面对流热交换的情况，有

式中：η为混凝土结构表面热交换系数，kJ/（m2·h·℃）；S为物体表面温度，Sa为环境温度，℃。

第四类边界条件为两种固体接触良好，接触面上的温度和热流量都是连续的，有

式中：S1、S2分别为接触面上两种固体的温度，℃。

3 参数确定及计算

3.1 参数确定

3.1.1 绝热温升

绝热温升是指混凝土结构不与外界发生任何热交换，混凝土的水化热全部转化为混凝土的温度［8］。绝热温升计算公式如式（7）所示，即

其中θmax=，

式中：θ（t）为混凝土龄期为t时的绝热温升，θmax为最大绝热温升，℃；t为混凝土龄期，d；m为常数，随水泥品种、比表面积及浇筑温度的不同而不同；mv为单位体积混凝土的水泥用量，kg/m3；k为掺合料折减系数，粉煤灰取0.25～0.30；F为活性掺合料用量，kg/m3；Q为单位质量胶凝材料的水化热总量，kJ/kg；c为混凝土的比热容，kJ/（kg·℃）。

3.1.2 热传系数

混凝土表面采用不同的保温材料，不同保温材料热传系数计算公式如式（8）［8］所示，即

式中：β为保温层的热传系数，W/（m2·℃）；βq为空气层的热传系数，设置为23 W/（m2·℃）；λi为各保温层材料的导热系数，W/（m·℃）；δi为各保温层材料的厚度，m。

3.1.3 混凝土弹性模量

混凝土的弹性模量可以按式（9）［9］计算，即

式中：E（t）为龄期t时混凝土的弹性模量，MPa；t为混凝土龄期，d；H为混凝土中掺合料对弹性模量的修正系数，根据掺合料的掺量取值；E0为混凝土最终弹性模量，一般取标准养护条件下28 d 龄期的弹性模量，MPa；w、b为系数，通过试验确定，无试验数据时分别取近似值0.4、0.6。

3.1.4 混凝土抗拉强度

文献［9］表明，混凝土的轴心抗拉强度在一定情况下是混凝土的真实抗拉强度，控制混凝土的开裂应以轴向抗拉强度为依据。t龄期的混凝土的轴心抗拉强度可按式（10）进行计算，即

式中：P（t）为t龄期的混凝土轴心抗拉强度，P为28 d 龄期的混凝土轴心抗拉强度标准值，MPa；γ为系数，通过试验确定，无试验数据时取近似值0.3；t为混凝土龄期，d。

3.1.5 环境温度

环境温度通常采用正弦函数或常数拟合。当昼夜温差较为显著时，采用正弦函数拟合；当环境温度变化幅度不大时，可简化为常数模拟。正弦函数拟合公式如式（11）［10］所示，即

式中：F（t）为环境温度，A为环境温度正弦变化的幅值，A0为平均温度，℃；t为混凝土龄期，t0为混凝土浇筑的迟延龄期，d。

3.1.6 抗裂性能

文献［9］表明，混凝土的抗裂性能可以用式（12）判断，即

式中：u为掺合料对混凝土抗拉强度的影响系数；t为混凝土龄期，d；σ1为混凝土结构第一主应力，MPa；K为混凝土抗裂安全系数，通常取1.15。

3.2 参数计算

五峰土家族自治县新建的T 梁桥采用C50 混凝土，根据《普通混凝土配合比设计规程》［11］（下面简称“设计规程”）和《公路桥涵施工技术规范》［12］相关规定，采用C50 混凝土的预制T 梁，设计配合比（质量比）为：水∶水泥∶粉煤灰∶砂∶石=0.43∶1∶0.32∶1.50∶2.91，同时掺入减水剂，减水率达到25%。

根据文献［9，13］，C50 混凝土参数设置如下：容重为25.0 kN/m3，28 d 龄期的弹性模量为34 500 MPa，泊松比为0.2，抗拉强度标准值为2.65 MPa，抗压强度标准值为32.4 MPa，热膨胀系数为1×10-5，比热容c为0.97 kJ/（kg·℃），热导率为10.6 kJ/（m·h·℃）。

根据文献［13］，C50 混凝土收缩徐变参数设置如下：28 d 龄期压缩强度为48 MPa，开始收缩时的混凝土龄期为3 d，周围环境相对湿度为70%，水泥系数为5，粉煤灰掺量为24%。

根据上述数据及预制T 梁的结构对称性，利用Midas FEA NX 软件建立三维有限元模型，忽略部分倒角和小型孔洞（预应力波纹管通道）［14］；再经过Midas FEA NX 的网格划分［15］，得到四面体单元315 372 个。有限元模型如图2所示。

图2 有限元模型Fig. 2 Finite element model

为研究方便，在边界上，施加两个方向的对称边界条件；在荷载上，仅考虑热源和对流，不考虑结构自重。

根据上述参数及公式（7），考虑到预制T梁混凝土拌合时采用预冷骨料、加冰等办法［8］控制混凝土的初始温度，将公式（7）中m取0.34（将初始温度设置为15 ℃）、k取0.25、Q根据以往试验的经验取375 kJ/kg、c取0.97 kJ/（kg·℃）、ρ取2 450 kg/m3，根据混凝土配合比得到mv=397.27 kg/m3、F=125.45 kg/m3，从而得到C50 混凝土的最大绝热温升为67.64 ℃，进而得到混凝土的绝热温升随龄期的变化规律。

在热传系数计算时，在T 梁侧模、端模考虑1 cm 厚钢模板，查阅文献［8］得钢材导热系数为58 W/（m·℃），根据式（8）得到T 梁侧模、端模的热传系数为22.9 W/（m2·℃）；T 梁的顶板上表面直接与空气接触，从而得到T梁顶面热传系数为23 W/（m2·℃）；T 梁的底面依次为3 cm 钢板、40 cm 高的混凝土台座、100 cm 深的碎石土，查阅文献［8］将混凝土台座和碎石土的导热系数分别设置为2.33 W/（m·℃）、1.172 W/（m·℃），计算得到T 梁底面的热传系数为0.975 W/（m2·℃）。

由于C50混凝土的胶凝材料中含有24%的粉煤灰掺量，查询文献［9］得到混凝土弹性模量的修正系数H=0.985；由于没有试验数据，式（9）中的b、w分别取近似值0.6、0.4，从而得到混凝土的弹性模量随龄期的变化规律，再由式（10）得到预制T梁混凝土抗拉强度随龄期的变化规律。

在环境温度设置上，由于严格控制梁场室内温度，使得梁场内部温度变化不大，在计算中采用常数函数模拟环境温度，设置为恒定20 ℃；计算时间段设置为预制T 梁混凝土浇筑完成后的28 d，并设置30 个增量步，采用位移与内力双重控制，保证计算精度。

4 水化热效应分析

通过Midas FEA NX 软件分析预制T 梁的水化热效应，得到28 d 内各龄期预制T 梁的温度变化情况和第一主应力变化情况，进而得到预制T梁的最高、最低温度变化情况和温度应力最大值变化情况，分别如图3～图4所示。

图3 预制T梁温度变化曲线Fig. 3 Temperature variation curve of prefabricated T-beam

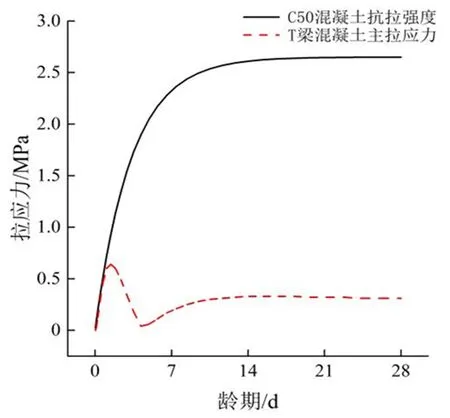
图4 预制T梁温度应力最大值变化曲线Fig. 4 Variation curve of the maximum temperature stress of prefabricated T-beam

由图3 可见，预制T 梁的最高温度变化为一条曲线，曲线的最高温度为28.59 ℃，出现在1.43 d 附近；预制T 梁的最低温度变化为一条直线，最低温度为20 ℃，最大温差为8.59 ℃，同样出现在1.43 d附近。

由图4 可见，预制T 梁28 d 内的温度应力均在C50 混凝土的抗拉强度范围内，且呈现先增大后减小再增大的变化趋势，表现为1.43 d 时达到最大温度应力0.64 MPa，4.20 d 时下降到0.04 MPa，14.10 d 时再上升到0.33 MPa，即28 d 内的温度应力最大值为0.64 MPa。

综合图3、图4，发现预制T 梁的最大温差与最大温度应力均出现在相同的时间点，即1.43 d。提取1.43 d时T梁的温度场和应力场，结果如图5所示。

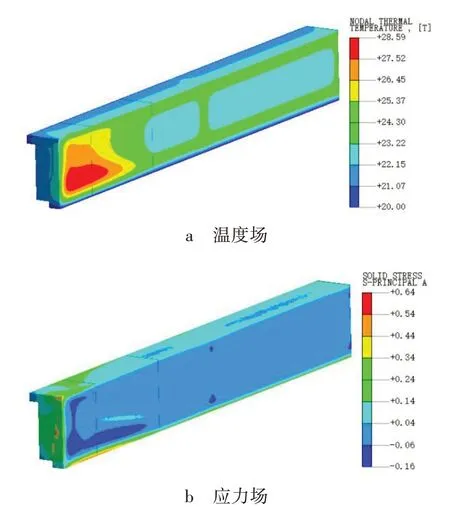
图5 1.43 d龄期预制T梁的温度场与应力场Fig. 5 Temperature field and stress field of prefabricated T-beam at 1.43 days of age

由图5 可见，预制T 梁的最高温度出现在梁端肋板的马蹄部位内部（此区域的腹板厚度最大，约60 cm），此时肋板马蹄部位的内部处于受压状态，主压应力最大值约0.16 MPa；主拉应力（最大值为0.64 MPa）主要出现在肋板马蹄部位的外表面与横隔板相交的棱角位置，以及局部转角位置。

根据文献［9］，24%粉煤灰掺量的掺合料对混凝土抗拉强度的影响系数u约为1.0，由式（12）计算各龄期的混凝土抗裂系数，并与混凝土抗裂安全系数进行对比，如图6所示。

图6 预制T梁抗裂性能评价Fig. 6 Crack resistance evaluation of prefabricated T-beam

由图6 可见，28 d 龄期内的混凝土抗裂计算系数均不小于抗裂安全系数1.15，即28 d 龄期内预制T梁发生开裂的风险不大；在0.2～2.4 d龄期内，混凝土抗裂系数均在3.0以下，接近抗裂安全系数，因此0.2～2.4 d龄期是预制T梁温度应力控制的关键期，应当加强养护。

5 水化热效应影响因素

5.1 混凝土配合比

上面分析中的C50混凝土采用的是添加减水剂和掺合料的配比（以下简称“原配比”），为了研究减水剂、掺合料对C50 混凝土水化热效应的影响，现对C50混凝土配合比进行修改。

配比一：不使用减水剂、掺合料。通过计算需要使用42.5 级水泥696.97 kg/m3，最大绝热温升为109.98 ℃；

配比二：使用减水剂，但不使用掺合料。通过计算需要使用42.5 级水泥522.72 kg/m3，最大绝热温升为82.48 ℃；

配比三：不使用减水剂，但使用掺合料。通过计算需要使用42.5 级水泥529.70 kg/m3、粉煤灰167.27 kg/m3，最大绝热温升为90.18 ℃。

将以上3 种配比的混凝土材料分别运用于预制T 梁的C50 混凝土，并进行水化热分析，得到28 d 龄期内3 种配比的温度应力最大值变化情况，如图7所示。为便于比较，将原配比条件的温度应力、C50混凝土抗拉强度也一起列示于图7。

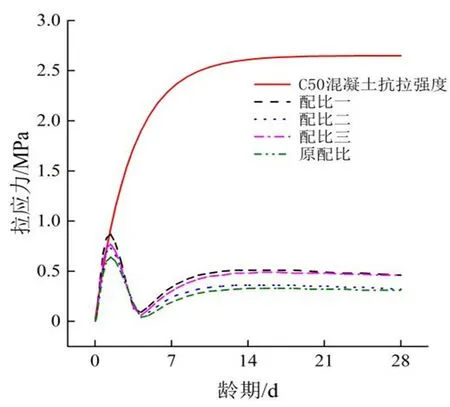
图7 混凝土配合比对预制T梁温度应力的影响Fig. 7 Influence of concrete mix ratio on temperature stress of prefabricated T-beam

由图7可见，除了原配比，其余配比的温度应力均有部分龄期超过C50 混凝土的抗拉强度，其中配比一的温度应力超过C50混凝土抗拉强度的龄期为0.3～1.3 d，温度应力最大值超出抗拉强度28.99%；配比二的温度应力超过C50 混凝土抗拉强度的龄期为0.5～0.85 d，温度应力最大值超出抗拉强度5.26%；配比三的温度应力超过C50 混凝土抗拉强度的龄期为0.4～1.08 d，温度应力最大值超出抗拉强度12.82%。

5.2 昼夜温差

上面水化热效应分析中的环境温度采用的是常数函数模拟，当预制T梁采用室外养护时，昼夜温度变化明显，应采用式（11）进行模拟。

现将环境温度正弦变化幅值A分别设置为2、4、6 ℃，平均温度均为20 ℃，从而得到昼夜温差分别为4、8、12 ℃的计算模型，即模型一、模型二、模型三。通过计算得到各模型T梁的温度应力最大值变化情况，如图8所示。为便于比较，将常数函数模拟昼夜温度的原模型也一起列示于图8。

图8 昼夜温差对预制T梁温度应力的影响Fig. 8 Influence of diurnal temperature difference on temperature stress of prefabricated T-beam

由图8 可见，预制T 梁在昼夜温差变化较大的情况下，温度应力均出现超过C50 混凝土的抗拉强度的情况，其中模型一的温度应力超过C50混凝土抗拉强度的龄期为0.60～0.80 d，温度应力最大值超出抗拉强度5.19%；模型二的温度应力超过C50 混凝土抗拉强度的龄期为0.47～0.95 d，温度应力最大值超出抗拉强度26.83%；模型三的温度应力超过C50 混凝土抗拉强度的龄期为0.37 ～0.95 d，温度应力最大值超出抗拉强度54.64%。

5.3 寒潮

上面水化热分析中C50混凝土在室内恒温养护，没有考虑寒潮的影响。现以5.2 节中模型三为基础，对环境温度变化进行修改，研究寒潮对预制T梁温度应力的影响。

寒潮模拟总时长为3.5 d，分为寒潮开始、寒潮持续、寒潮结束3个阶段。寒潮开始阶段，环境温度下降，在0.625 d 内由20 ℃线性下降至5 ℃；寒潮持续阶段，环境温度保持在5 ℃，持续2.25 d；寒潮结束阶段，环境温度上升，在0.625 d 内由5 ℃线性上升至20 ℃。

为研究寒潮对预制T 梁温度应力的影响，分别在混凝土龄期0.5、2.5、4.5、6.5 d 设置寒潮时间点，从而形成模型四、五、六、七，进而得到各模型的预制T梁温度应力最大值的变化情况，如图9所示。为便于比较，将不考虑寒潮情况下预制T梁的温度应力最大值（模型三）也一起列示于图9。

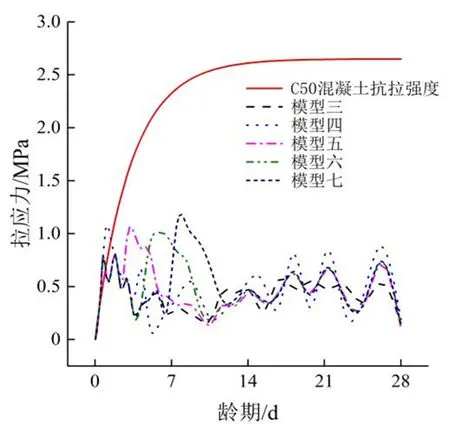
图9 寒潮对预制T梁温度应力的影响Fig. 9 Influence of cold wave on temperature stress of prefabricated T-beam

由图9 可见，预制T 梁在遭遇寒潮之后，温度应力均会显著上升，对后期的温度应力产生一定程度的影响，因而需要注意寒潮对混凝土结构的破坏。

6 结论

通过预制T 梁的水化热效应分析，得出以下结论。

（1）在室内恒温养护下，预制T梁的主拉应力在1.43 d 的龄期达到最大值0.64 MPa，最高温度出现在梁端肋板的马蹄部位内部，主拉应力通常出现在梁端位置的外表面。

（2）通过使用外加剂或掺合料代替部分水泥可以显著降低水泥的使用量，从而降低绝热温升，并在一定程度上降低预制T 梁的温度应力。因此，在预制T 梁温度应力较大时可以考虑使用外加剂、掺合料来优化混凝土配合比。

（3）昼夜温差分别为4、8、12 ℃时，预制T 梁超过C50 混凝土抗拉强度的龄期分别出现在0.60～0.80 d、0.47～0.95 d、0.37～0.95 d，超出抗拉强度的幅度分别为5.19%、26.83%、54.64%，即昼夜温差越大，预制T 梁产生的温度应力超过混凝土抗拉强度的幅度和龄期范围越大。

（4）预制T梁在遭遇寒潮之后，温度应力显著升高。在混凝土浇筑后的早期，由于混凝土抗拉强度较低，应当注意防范寒潮带来的不利影响。