掺砂软黏土一维压缩和渗透性状研究

姚 达，花叶琦，夏竹岭，徐键强

（江苏鸿基水源科技股份有限公司，江苏 扬州 225000）

我国东南沿海地区分布着大量的软黏土。在软土地基上修建建筑物，易整体下沉，从而产生裂隙、倾斜，甚至倒塌等危害。因此必须对软土地基进行加固处理，才能满足房屋建筑、道路交通等工程建设的需要，避免工程灾害的发生［1］。

真空预压法因加固成本低，加固过程中土体不易产生失稳破坏，且施工简单，加固后土体沉降、强度等能够满足设计要求［2-5］，从而在工程建设中得到广泛应用。但真空预压法存在深层土体加固效果较差的问题，难以满足对加固效果有更高要求的深厚软基加固，极大限制了该技术的应用范围［6］。

近年来，众多学者研究表明掺砂能改变土体的力学性能，提高深层土体的加固效果。许丰岐［7］发现掺砂对真空预压加固吹填土有积极作用，掺砂后土体的排水量增大，加固后土体的含水率降低；武亚军等［8］探讨了掺砂对沉降特性的影响，发现随着掺砂率的增加，土体沉降速率加快，且初始含水率越低，掺砂效果越明显；兰恒水等［9］研究表明，掺砂后改良土无侧限强度和直剪强度有较大提高，从改良土体物理力学特性及掺砂成本等方面综合考虑，掺砂改良高液限土掺砂比例宜为20%左右；谭杰等［10］向淤泥土中掺入砂土，探讨了复合土的渗透系数，结果表明，在一定掺砂范围内（20%～40%），掺砂率越高，渗透系数越大，且土体的压缩系数越低，掺砂越能加快土体的固结，但是其讨论的掺砂率较高，在实际操作中会提高施工成本和作业的困难程度。

为合理指导现场施工，明确低掺砂率时土体掺砂后的压缩性状和渗透性状，本文开展了掺砂率（质量分数）为0、5%、10%、15%、20%、25% 的土体压缩试验和渗透试验，分析了掺砂对压缩曲线特征的影响，探讨了掺砂土体压缩系数和压缩指数、渗透系数和渗透指数随掺砂率的变化规律，给出了掺砂影响下的土体归一化压缩公式，提出了压缩指数和渗透指数与掺砂率的关系式，以期为负压掺砂土体固结预测及加固效果提供参数支持和理论支撑。

1 试验方案

1.1 试验材料

试验用土为浙江省台州市路桥区淤泥质软土，根据室内土工试验方法测得的土样基本物理参数如表1 所示。其中，土体液限和塑限采用液塑限联合测定法测定，比重采用比重瓶法测定，土颗粒粒径分布由密度计法测定。

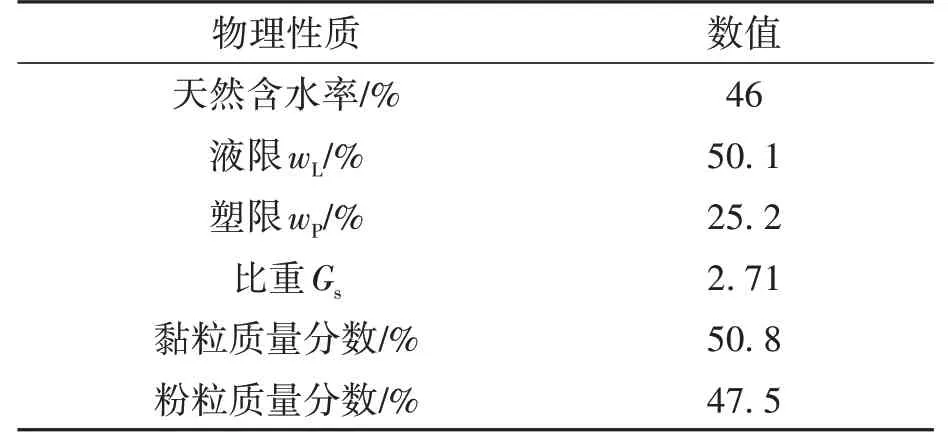
表1 试验用土基本物理性质Table 1 Basic physical properties of test soil

由表1 的土体液限和塑限性质可知，试验土样为高液限黏土。试验用砂产地为浙江台州，颗粒级配见图1，砂的不均匀系数为1.46，曲率系数为0.97，属于不良中砂。

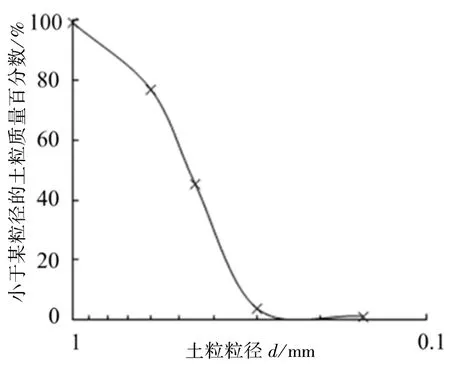
图1 砂的颗粒级配Fig. 1 Grain gradation of the sand

1.2 试验设备

试验模型由试验模型箱、真空排水系统和量测系统组成，如图2 所示。模型箱尺寸为φ30 cm×60 cm，真空排水系统由真空泵、排水板、塑料软管、集水瓶组成，量测系统由百分表、电子天平、真空表等组成，其中模型箱、集水瓶和真空泵如图3所示。

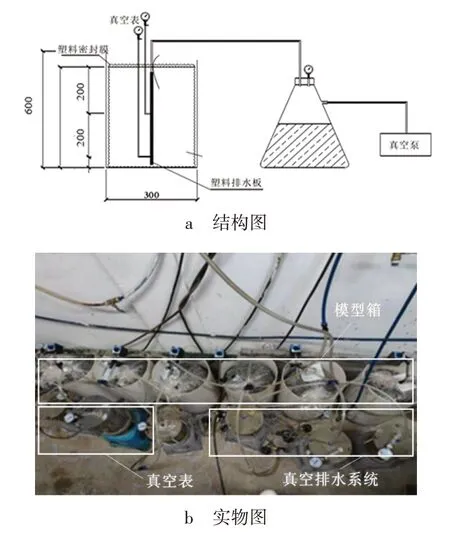
图2 室内模型试验图Fig. 2 Test map of indoor models

图3 试验模型实物图Fig. 3 Physical map of test model

1.3 试验步骤

将从工地取回的土样晒干磨碎，经过0.075 mm 的孔径细筛，测定风干含水率；取满足模型箱要求的一定质量的干土5 kg，配置成初始含水率（质量分数）为60%的土样，分别掺入0、5%、10%、15%、20%、25%（干砂质量与土中土颗粒质量之比）的干砂；充分搅拌均匀后置入模型箱中开展真空预压试验，负压荷载为-90 kPa。当总沉降H随时间t的曲线趋于水平、集水瓶在12 h 内质量不发生改变时，即可认为土体达到稳定状态，可结束抽真空。

考虑不同掺砂率对真空预压效果的影响，在排水板中间及中间以下15 cm 处各设置真空表1个，在土体表面靠近模型箱边缘处设置百分表1个，分别测量并记录土体沉降量、排水板及土中真空度、出水量。

试样固结稳定后，沿试样径、竖向不同位置取不同掺砂率的掺砂软土，检测土体含水率、十字板强度，并开展一维固结渗透试验，试验过程中，严格按照《土工试验方法标准》（GB/T 50123—2019）［11］的要求进行数据记录和分析。

压缩试验采用常规固结仪加载，试样直径为61.8 mm、高度为20 mm，加荷0～1 600 kPa，加荷杠杆比为1∶1，起始荷载为12.5 kPa。每级加荷稳定后，进行渗透试验，开展变水头渗透系数测定；然后根据掺砂土体沉降和渗透数据，分析不同掺砂率下土体的压缩和渗透性状。

2 压缩性状分析

2.1 压缩曲线形态分析

经压缩试验得到不同掺砂率的软土压缩曲线如图4所示。

图4 固结压缩曲线Fig. 4 Consolidation compression curve

由图4 可知，不同掺砂率的软土压缩曲线形态相近，均呈凹型，且掺砂率低的土样压缩曲线始终位于掺砂率高的土样上方，即随着掺砂率的增加，土中初始孔隙比随着掺砂率的增加而减小；在初始固结阶段，不同掺砂率的疏浚泥固结压缩曲线差异较大，但随着竖向有效应力的增加，不同掺砂率的土体固结压缩曲线之间的差异越来越小，最后近似于发展成平行关系。这是由于对于同一掺砂粒径，试样掺砂率越大，试样内部所含黏粒越少、砂粒越多，从而在试样内部产生更多的砂粒-黏粒接触面，导致孔隙比e减小。

从图4 还可以看出，土体中的掺砂率从0 增加到25%，且荷载从0增加到1 600 kPa时，孔隙比e不断减小，最终减小幅度均在45%左右。

2.2 掺砂软土归一化压缩公式

Nagaraj等［12］通过引入归一化参数e/eL（eL为液限下的孔隙比），提出孔隙比与其他参数的曲线归一化方法，Achari 等［13］通过渗透试验发现，Nagaraj 等提出的数据存在偏差，需要对试验数据进行归一化处理，从而获得了液限为40%～60%的软黏土渗透系数预测表达式。

本文所用的土体液限为50.1%，掺砂25%后土体液限变化为38.0%，引入归一化压缩指标e/eL对压缩曲线进行归一化处理后，结果如图5所示，进而得到不同掺砂率的台州软土归一化经验公式，如式（1）所示，即

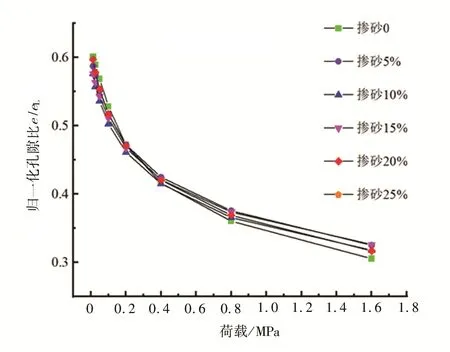
图5 归一化孔隙比与荷载关系Fig. 5 Relationship between normalized void ratio and load

从图5 可以看出，在低压力范围内（小于400 kPa），掺砂土体的归一化规律较好；而在800 kPa和1 600 kPa荷载下，掺砂土体的归一化孔隙比则有一定的差异。

目前传统的真空负压荷载为100 kPa，因此，对于各初始含水率及掺砂率不同的掺砂软土可以利用压缩指标的归一化公式进行分析。

2.3 掺砂率对压缩系数和压缩指数的影响

压缩系数为压缩试验所得e-p压缩曲线上某一压力段割线的斜率，通常用来评价土体压缩性的大小，压缩系数越大，压缩性越高。压缩系数计算公式如式（2）所示，即

式中：av为土样的压缩系数，MPa-1；pi为单位压力值，i=1，2，…，6；ei为pi作用下的孔隙比。

图6 为压缩系数与平均荷载的关系曲线，图中各点的横坐标为相邻两荷载的平均值。从图6可以看出，压缩系数av随着荷载增大而减小，也随着掺砂率的增加而减小，且减少的幅度越来越缓慢；不掺砂土体的压缩系数始终高于掺砂土体的压缩系数。

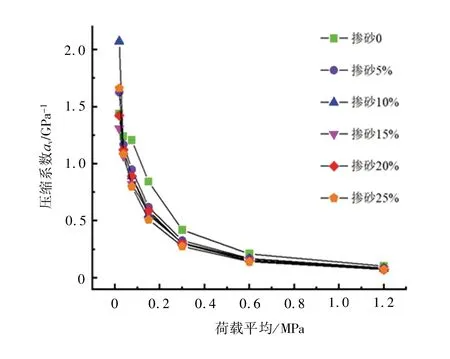
图6 压缩系数av与平均荷载的关系Fig. 6 Relationship between compression coefficient av and average load

显然，掺砂改善了土体的结构，降低了土体的压缩性。

压缩指数为e-lgp压缩曲线上大于先期固结应力后直线段的斜率，表达式为

式中：cc为土样的压缩指数，kPa-1。

图7 为压缩指数与平均荷载的关系曲线，图中各点的横坐标为相邻两荷载的平均值。

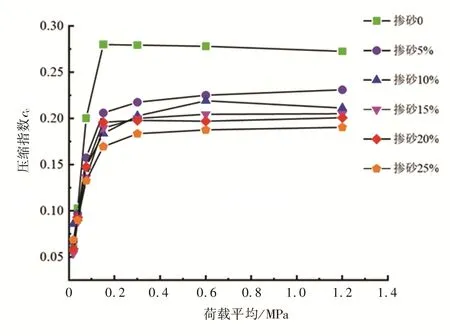
图7 压缩指数Cc与平均荷载的关系Fig. 7 Relationship between compression index Cc and average load

从图7可以看出，掺砂率为0～25%时，压缩指数在平均荷载200 kPa 之前随平均荷载的增加而急剧上升，在平均荷载200 kPa 之后趋于平缓；不掺砂土体的压缩指数大于掺砂土体，且随着掺砂率的增加压缩指数逐渐减小。

由上可知，压缩系数、压缩指数均随着掺砂率的增加而减小，它们的关系如式（4）、式（5）所示，即

式中：a1-2为压力值100 kPa和200 kPa时的压缩系数；cs为掺砂率。

由式（4）、式（5）得出它们的曲线，如图8、图9所示。

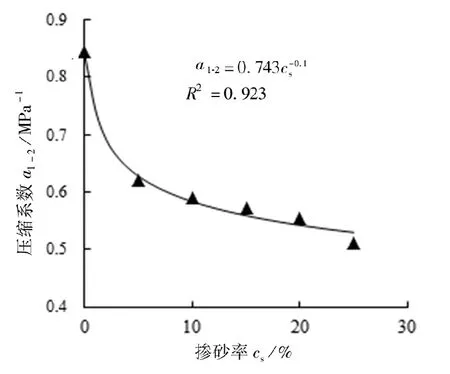
图8 压缩系数a1-2与掺砂率cs关系Fig. 8 Relationship between compression coefficient a1-2 and sand mixing ratio cs

图9 压缩指数cc与掺砂率cs关系Fig. 9 Relationship between compression index cc and sand mixing ratio cs

由图8、图9可以看出，掺砂土体的压缩系数、压缩指数均随着掺砂率的增加而非线性减小，当掺砂率小于5%时，压缩系数和压缩指数均随着掺砂率的增加而明显下降，这与章镇宁等［14］研究成果相吻合；当掺砂率接近20%时，压缩指数降低趋势变缓，压缩性降低；掺砂率为25%时，压缩系数、压缩指数较不掺砂时分别降低了39.3%和35.7%，土体抗压缩性极大提升。

2.4 渗透性状分析

土体渗透性状通常用渗透系数与渗透指数来表示。土体的渗透系数在固结过程中随应力的增加呈现非线性变化［15］，目前常用e-lgk模型表征渗透系数的变化规律，其中k为土体渗透系数，可以通过变水头试验测得。

e-lgk关系如图10所示。

图10 e-lg k变化曲线Fig. 10 The change curve of e-lg k

从图10 可以看出，掺砂率相同时，掺砂土体的渗透系数随着孔隙比的增大而增大；孔隙比相同时，渗透系数随着掺砂率的增大而增大。说明掺砂能提高土体的渗透性能，从而加快土体的固结速率。

从图10 还可以看出，当掺砂率为0 时，土体的孔隙比随荷载变化较大，但渗透系数随荷载变化较小，且渗透系数基本维持在10-8数量级；随着掺砂率的增加，尤其是掺砂率接近20%时，掺砂土体加载前后渗透系数能发生1 个数量级的变化，进一步验证了土体渗透系数随固结过程的非线性减小规律。因此，固结过程中若不考虑渗透系数的变化，将会引起较大的计算误差。

按照文献［16］，渗透指数cz计算公式如式（6）所示，即

式中：e0表示初始孔隙比；k0表示初始渗透系数。

渗透指数cz与掺砂率cs的关系如图11 所示，计算公式如式（7）所示，即

图11 渗透指数与掺砂率关系Fig. 11 Relationship between permeability index and sand mixing ratio

从图11 可以看出，渗透指数cz随掺砂率的增加而逐渐减小。

另外，有研究表明，渗透指数cz与初始孔隙比e0存在线性相关关系［17］。对于本文掺砂软土，cz与e0良好的线性关系如图12 所示，计算公式如式（8）所示，即

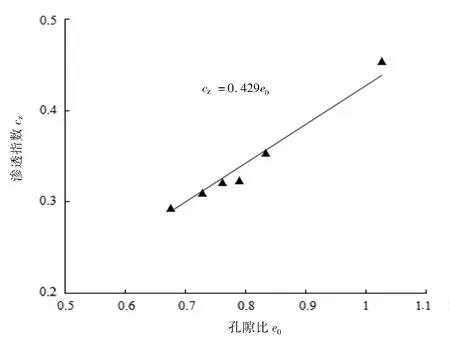
图12 渗透指数与孔隙比关系Fig. 12 Relationship between permeability index and void ratio

3 结论

通过室内一维固结渗透试验，对不同掺砂率影响下的软土液塑限、压缩性及渗透性进行对比分析，得出以下结论：

（1）不同掺砂率的土体压缩曲线形态相近，在固结后期接近于平行关系；掺砂率低的土样压缩曲线始终位于掺砂率高的土样上方；与初始孔隙比相比，1 600 kPa 荷载下的孔隙比减小幅度均在45%左右，掺砂率对孔隙比降低率没有影响。

（2）掺砂软土的压缩规律可用指标e/eL进行归一化描述；掺砂土体的压缩系数、压缩指数均随着掺砂率的增加而非线性减小；掺砂率相同时，掺砂土体的渗透系数随着孔隙比的增大而增大；孔隙比相同时，渗透系数随着掺砂率的增大而增大。掺砂增大了土体的抗压缩性和渗透性。

（3）压缩系数、压缩指数和渗透指数均与掺砂率存在良好的幂函数关系，工程中可根据掺砂率推算软土的压缩和渗透参数。