基于Skempton有效应力原理的岩石压缩系数研究

毛小龙，刘月田，关文龙，刘思平，李 骏

(1.中国石油大学(北京) 石油工程教育部重点实验室，北京 102249；2.中国石油勘探开发研究院，北京 100083)

引 言

不同于连续固体介质材料，岩石因内部孔隙的存在有3个体积：表观体积Vb、基质颗粒体积Vs和孔隙体积Vp。饱和流体岩石的应力应变同时受孔隙流体压力p和外部总应力σ两个作用力影响，基于岩土工程、油藏工程、地下水工程、地球物理等不同领域的基础研究需求，岩石在等温条件下至少有恒流压下的表观压缩系数Cbσ、基质压缩系数Csσ、孔隙压缩系数Cpσ和恒总应力下的表观压缩系数Cbp、基质压缩系数Csp、孔隙压缩系数Cpp6个压缩系数。然而传统的压缩系数研究多基于适用于土力学的Terzaghi[1-2]有效应力原理，在测试、计算、使用岩石各压缩系数中常将各压缩系数之间的关系混淆，在研究岩石各压缩系数变化规律和相互关系中也常出现相互矛盾的认识，例如：李传亮[3-6]、王历强[7]等学者认为岩石孔隙压缩系数与孔隙度正相关，与基质颗粒压缩系数关系密切；张津宁[8]、高有瑞[9]、罗瑞兰[10]等学者则认为岩石孔隙压缩系数与孔隙度负相关，与岩石表观压缩系数关系更为密切。因此，理清岩石的多个压缩系数，得到岩石各压缩系数之间的关系式和一组可定量计算岩石各压缩系数的计算式是十分必要的。本文基于广泛适用于岩石、混泥土、土体的Skempton[11]有效应力原理，对岩石在恒流压、恒总应力、封闭条件下的表观压缩系数、孔隙压缩系数和基质颗粒压缩系数进行了系统研究，推导了岩石各压缩系数在3种不同应力条件下的关系式，得到一组岩石各压缩系数的定量计算式，并进行了实例论证。

1 两个有效应力原理下的岩石压缩系数分析

基于岩土工程、油藏工程、地下水工程、地球物理等不同领域的基础研究需求，岩石恒流压下的表观压缩系数Cbσ、基质压缩系数Csσ、孔隙压缩系数Cpσ和恒总应力下的表观压缩系数Cbp、基质压缩系数Csp、孔隙压缩系数Cpp定义为

(1)

式中：Vi中i取b、s、p，即为Vb表观体积、Vs基质颗粒体积和Vp孔隙体积，m3；σj中j取1、2，即σj分别为总应力σ、流压p,MPa；Cij为压缩系数，MPa-1，为保证数值为正，(-1)j在总应力σ取1，在流压p下取2。

各学科还定义了一些其他压缩系数：油藏工程中，定义了单位岩石体积中孔隙体积随流体压力的变化率Cf和综合压缩系数Ct(油藏流体压力每降低1 MPa，由于油藏的岩石孔隙体积缩小、储存的流体因膨胀而从单位体积岩石孔隙中排出的流体总体积)

(2)

Ct=Cf+φCl。

(3)

式中：Cl为孔隙饱和流体压缩系数，MPa-1；φ为孔隙度，%。

地球物理探测中，定义了在干燥孔隙开放或恒孔隙流压下岩石表观压缩系数Cdry和在封闭不排水条件下岩石表观压缩系数Csat。岩土工程中，定义了岩土2个最常用的压缩系数：基质颗粒压缩系数Cs和恒流压表观压缩系数C。这些压缩系数都是岩石在不同领域研究的基础物性参数，具有举足轻重的意义。而传统的岩石压缩系数研究多基于Terzaghi有效应力原理，例如秦积舜、李爱芬主编的教材《油层物理学》[12]定义岩石的几个压缩系数时采用了Terzaghi有效应力，Terzaghi有效应力原理表达式为

σeff=σ-p。

(4)

基于Terzaghi有效应力原理，岩石的各压缩系数关系有

(5)

(6)

Csσ=Csp=Cs=0。

(7)

假设基质颗粒不可压缩，孔隙体积变化等于岩石表观体积变化，则

(8)

(9)

Ct=Cf+φCl=φ(Cpp+Cl)。

(10)

然而，与松散土体不同，储层岩石是固结的，岩石的应力应变不仅有颗粒间滑动变形还有颗粒的体积变形。适用于岩石、混泥土、土体体积应变的Skempton有效应力原理同时考虑了颗粒体积变形和颗粒间滑动变形。Skempton有效应力下的岩石表观体积应力应变计算式为

(11)

(12)

这与Biot[13]、Gassmann[14]、Geertsma[15]、Bishop[16]等学者基于不同角度研究得到的认识一致，充分论证了其对于岩石应力应变的适用性。基于Skempton原理分析岩石的各压缩系数有：

1)恒流压Δp=0，岩石的应变变化量

Δεb=-CΔσ，

(13)

对应的压缩系数

(14)

2)恒总应力Δσ=0，岩石的应变变化量

Δεb=(C-Cs)Δp，

(15)

(16)

式(16)表明，恒总应力下的岩石表观压缩系数为恒流压下的岩石表观压缩系数与基质颗粒压缩系数之差。

3)岩石在封闭不排水条件下，总应力变化Δσ，根据Bishop[16]对应孔隙流压变化

(17)

代入Skempton方程得到应变变化量

(18)

对应的压缩系数

(19)

在地球物探学中，表达岩石的干燥骨架、固体基质和孔隙流体的体积模量Gassmann方程[14]为

(20)

压缩系数为体积弹性模量的倒数，用压缩系数形式代入方程(20)整理得

(21)

结合不同学科压缩系数的定义，恒流压下的岩石表观压缩系数含义一致，

Cdry=Cbσ=C。

(22)

结合式(22)，对比式(19)和式(21)，Skempton方程推导的封闭条件下的岩石表观压缩系数关系式(19)与Gassmann方程压缩系数表达式(21)一致。基于Skempton有效应力原理很好地理清岩石3种不同应力下的表观压缩系数的关系，而油藏工程、地下水工程中在不同应力变化条件下的岩石孔隙体积应变及孔隙压缩系数则需要进一步推导得到。

2 不同应力条件下的孔隙压缩系数关系式

采用Skempton有效应力方程计算岩石在不同应力条件下的表观体积变化ΔVb，减去对应应力条件的颗粒体积变化ΔVs，得到此时孔隙体积变化ΔVp，从而得到不同应力条件下的孔隙压缩系数。

2.1 恒流压孔隙压缩系数关系式

在恒流压变总应力条件下，根据Skempton有效应力，岩石表观体积变化

ΔVb=-CVbΔσ。

(23)

以穿过基质颗粒的受力面进行受力分析可知，基质颗粒平均作用力满足

σA=σs(1-φ)A+pφA，

(24)

(25)

恒流压变总应力条件下，作用在岩石基质颗粒的平均作用力变化

(26)

岩石基质颗粒体积变化

(27)

需要说明的是，岩石基质颗粒真实平均作用力σs变化下的压缩系数仍然为矿物颗粒压缩系数Cs，而以总应力为变量的岩石颗粒视压缩系数Csσ则为

(28)

岩石孔隙体积变化

ΔVp=ΔVb-ΔVs=-(C-Cs)VbΔσ=

(29)

恒流压变总应力下的岩石孔隙压缩系数

(30)

这一关系式与部分学者在油藏工程得到的常见岩石孔隙压缩系数关系式相同，然而本式只适用于恒流压变总应力条件，油藏工程、地下水开采通常是在恒总应力变流压条件下进行，本式并不适用，需要进一步推导。

2.2 恒总应力孔隙压缩系数新关系式

恒总应力Δσ=0，根据Skempton有效应力，岩石表观体积变化

ΔVb=(C-Cs)VbΔp；

(31)

恒总应力Δσ=0，基质颗粒体积应变的基质颗粒应力变化

(32)

对应的颗粒体积变化

CsφVbΔp。

(33)

岩石基质颗粒体积真实平均作用力σs变化下的压缩系数仍然为矿物颗粒压缩系数Cs，所以，流压变量的岩石颗粒视压缩系数

(34)

孔隙体积变化则为

ΔVp=ΔVb-ΔVs=[C-(1+φ)]VbΔp，

(35)

从而得到恒总应力变流压下孔隙压缩系数新关系式

(36)

根据表1和式(36)，孔隙度取0.02～0.35时，矿物颗粒压缩系数常在10-5MPa-1数量级，岩石表观压缩系数在10-5～10-4MPa-1数量级，计算得到孔隙压缩系数常在10-4～10-3MPa-1，与文献[8-10]测试结果一致。恒总应力下，岩石孔隙压缩系数常远大于岩石表观压缩系数，岩石表观压缩又大于基质颗粒压缩系数。

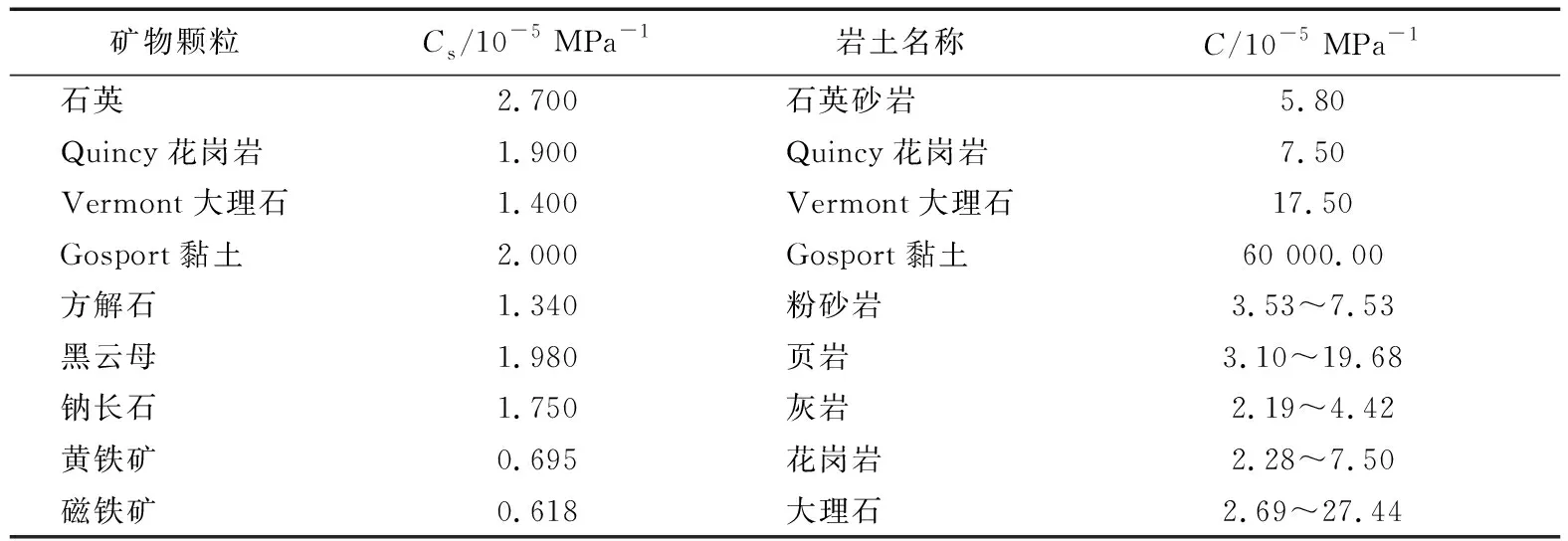
表1 常见矿物颗粒和岩土的压缩系数[11]Tab.1 Compression coefficient of common mineral particles and rock-soil[11]

根据式(36)和式(30)可知

(37)

这与岩石表观体积压缩的关系式一致，恒总应力孔隙压缩系数为恒流压孔隙压缩系数与基质颗粒压缩系数之差。

2.3 封闭条件下的孔隙压缩系数关系式

封闭不排水条件下，单位总应力变化量引起的岩石表观体积变化量

(38)

对应的岩石基质颗粒体积变化量

(39)

封闭条件下，单位总应力变化下的岩石颗粒视压缩系数

(40)

封闭不排水条件下，单位总应力变化量引起的岩石孔隙体积变化量

(41)

(42)

对应的封闭条件下，单位总应力变化对应的孔隙压缩系数

(43)

封闭条件下，单位孔隙压力变化对应的孔隙压缩系数

(44)

这组关系式正好论证了在封闭条件下以孔隙压力为变量的孔隙压缩系数与孔隙流体压缩系数相等的经验认识。基于Skempton有效应力原理的压缩系数关系式反应了岩石的应力应变机制，所得不同应力条件下的各压缩系数关系式可从不同角度得到论证。

3 储层岩石各压缩系数计算式

各学科在没有特殊说明的情况下，岩石表观压缩系数常指恒流压下的表观压缩系数C，基质颗粒压缩系数常指矿物颗粒压缩系数Cs，孔隙压缩系数Cp常指恒总应力孔隙压缩系数Cpp。从上面的关系式可知，不同应力条件下岩石的各压缩系数均可由Cs、C、Cl来表示，意味着岩石在不同应力条件下的各压缩系数均可以Cs、C、Cl为基础计算得到，基于Skempton有效应力，不同应力条件下岩石各压缩系数计算式总结如下：

1)岩石表观压缩系数在恒流压、恒总应力、封闭条件下的计算式分别为：

Cbσ=Cdry=C，

(45)

Cbp=Cbσ-Cs=C-Cs，

(46)

(47)

2)岩石孔隙压缩系数在恒流压、恒总应力、封闭条件下的计算式分别为：

(48)

(49)

(50)

3)岩石颗粒压缩系数恒流压、恒总应力、封闭条件下的真实压缩系数均为Cs，恒流压、恒总应力、封闭条件下视压缩系数计算式分别为：

(51)

(52)

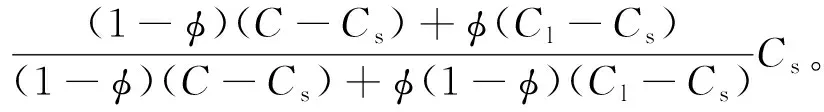
(53)

4)油藏工程生产中常用的2个压缩系数计算式则为：

Cf=φCpp=Cbp-φCs=C-(1+φ)Cs，

(54)

Ct=Cf+φCl=C-(1+φ)Cs+φCl。

(55)

4 应用举例

中石油勘探开发研究院从美国西弗吉尼亚州购得一批石油行业最好的油层物理测试标准岩心Berea砂岩，用于砂岩压缩系数、驱替过程中润湿性变化等油层物理基础研究。选用其中一块与文献[16]岩心相近的孔隙度为0.16的硅质细砂岩，实验室严格按照石油与天然气行业标准测得岩石物理基础物性参数，其中岩石压缩系数采用三轴向岩石压缩系数高精度测试仪按照SY-T5815-1993标准测得，压力表精度0.1%，实验误差小于5%。实验室测得的压缩系数结果为：恒流压下的表观体积压缩系数1.2×10-4MPa-1，基质平均压缩系数2.6×10-5MPa-1，恒总应力下的表观体积压缩系数为9.5×10-5MPa-1、孔隙压缩系数为5.7×10-5MPa-1。实验测试结果与文献[16]中孔隙度为0.15岩心测试的恒流压下表观压缩系数1.05×10-4MPa-1、基质平均压缩系数2.7×10-5MPa-1结果相符合。

而采用本文中以Cs、C、Cl为基础的新计算式，水的压缩系数取常用标准4.8×10-4MPa-1，可直接计算恒总应力表观压缩系数

Cbp=C-Cs=(12-2.6)×10-5MPa-1=

9.4×10-5MPa-1，

(56)

孔隙压缩系数

(57)

这2个岩石系数的计算结果都与实验测试结果非常接近，验证了计算式的准确性。此外，还可以利用这组计算式非常方便地计算其他应力条件下没有测试或者不太方便测试的压缩系数，可节约大量人力物力。将其他应力条件下的岩石各压缩系数代入对应的计算式得到计算结果分别为：Csat=6.7×10-5MPa-1，Cpσ=5.88×10-4MPa-1，Cpsatσ=2.71×10-4MPa-1，Csσ=3.10×10-5MPa-1，Csp=4.95×10-6MPa-1，Cssatσ=2.82×10-5MPa-1，Cf=8.98×10-5MPa-1，Ct=1.67×10-4MPa-1。计算结果与文献[15-16]认识一致，岩石在不同应力条件下定义的不同压缩系数，数量级从10-6～10-4MPa-1，差距可达2个数量级；在文献[10]低孔储层中，Cpp可达10-3MPa-1，差距可达3个数量级，不能混淆使用。

5 结 论

(1)Terzaghi有效应力原理不适用于岩石压缩系数研究，基于Skempton有效应力原理得到的岩石压缩系数在3种应力条件下的关系式准确厘清了不同学科岩石各压缩系数的相互关系。

(2)恒总应力下的岩石表观压缩系数、孔隙压缩系数分别为恒流压下对应的压缩系数与颗粒压缩系数之差，封闭条件下的岩石压缩系数关系式与Gassmann方程认识一致。

(3)在相同应力条件下岩石的孔隙压缩系数远大于表观压缩系数，表观压缩系数又大于颗粒压缩系数，不同岩石压缩系数之间差距可达2～3个数量级。

(4)以Cs、C、Cl为基础的一组岩石压缩系数新计算式反应了岩石应力应变机制，适用性好，计算简便，可在岩土工程、油藏工程、地下水工程和地球物探等学科广泛应用。