基于Nelder-Mead算法的PVD加热器结构优化

周皓天 ，张勤芳 ，卢 倩 ，龙汝磊

1.盐城工学院 机械工程学院，江苏 盐城 224051； 2.光驰科技(上海)有限公司，上海 200444

真空蒸发镀膜技术是指在真空环境中，通过物理气相沉积（physical vapor deposition，PVD）、化学气相沉积等手段，将金属等固体材料气化附着在产品物件表面并产生一层均匀的薄膜，以达到增强产品的抗腐蚀性、美观性以及改善产品的光学性能等目的［1］。薄膜沉积时镀膜机基板温度及均匀性是影响成膜质量的关键［2-6］。因此镀膜机基板表面温度均匀性优化及加热器结构改良已成为近年来的研究热点。

马玉春［7］以空间隔离原子层沉积系统为研究对象，通过对基底加热器进行温度补偿以及对喷头加热，提高了基底温度分布的均匀性。陈靖等［8］借助ANSYS 有限元分析软件研究了两种不同结构的加热器对蓝宝石基底温度分布的影响。赵丽丽［9］以原子层沉积系统为研究对象，通过有限元分析的方法研究了隔热板参数、基座高度以及基座参数对基板温度分布的影响。孙彦庆等［10］借助ANSYS建立了原子层沉积反应室模型，通过控制变量法分析了气体入口流量、电阻片与基座的加热距离以及加热温度对衬底表面温度分布的影响。Leigh 等［11］在研究微波等离子体增强化学气相法沉积纳米金刚石的过程中，借助温度映射技术探究了衬底台设计、微波功率和腔室压力对衬底温度均匀性的影响规律。May等［12］在一个基板面板上放置4 个不同温度的基板，使用分子束外延技术进行实验，研究了不同基板温度对样本生长速度的影响。Deng 等［13］将计算流体力学模拟与机器学习相结合，通过对仿真数据进行处理，利用神经网络模型对基底温度均匀性进行优化。以上成果研究了不同沉积方法下基板温度均匀性的优化方法以及温度对成膜质量的影响，但在真空蒸发镀膜技术中对基板温度均匀性的优化尚缺乏深入研究，导致基板温度均匀性影响机理不清晰，存在温度均匀性优化效率低的问题。

为解决上述问题，本研究借助COMSOL Multiphysics 5.6 有限元分析软件对真空蒸发镀膜机内基板表面温度分布规律进行探究，并使用单纯形法对加热系统的结构参数进行优化，达到提升基板表面温度均匀性的目的。

1 仿真模型

1.1 几何结构与模型简化

本研究仿真模型参照OTFC-1550 电子枪蒸发镀膜机建立，整体结构如图1 所示。镀膜机内部结构较为复杂，考虑到其中部分因素在加热过程中对基板温度影响较小，并会增加不必要的计算量，因此在不影响加热系统实际效果的前提下，对仿真模型作出如下假设：

图1 电子枪蒸发镀膜机模型结构Fig.1 Model structure of electron gun evaporation coating machine

（1）所有材料都是均匀且各向同性的；

（2）真空中主要换热方式为热辐射与热传导，不考虑对流换热；

（3）由于真空室与基板加热系统均为轴对称实体，因此将模型简化成二维轴对称模型，这对分析系统实际模型并无太大影响；

（4）建模中简化夹具以下部分；

（5）真空室外层装有循环水冷系统，在建模过程中将水冷系统简化成恒定温度壁面边界。

简化后的基板加热系统模型如图2所示。由图2可知，模型由真空室腔体、加热丝、辐射板、反射板、基板、基板夹具以及水冷系统组成。模型中真空腔体、辐射板、反射板以及基板夹具材质均为SUS304 奥氏体不锈钢，电热丝材质为Cr20Ni80 镍镉合金，基板材质为石英。基板尺寸φ30 mm×3 mm；虚线处为有效加热区，有效加热区弧长498 mm；顶部加热丝间距D1=14 mm，侧壁加热丝间距D2=30 mm，辐射板到反射板距离D3=2 mm，基板夹具底部到上辐射板加热距离L=400 mm，真空室腔体半径755 mm。

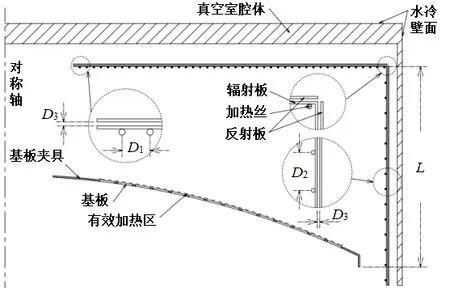
图2 简化后基板加热系统模型结构Fig. 2 Simplified rear substrate heating system model structure

1.2 控制模型

加热过程中镀膜腔体内部处于真空状态，气体极为稀薄，因此在传热过程中可以忽略对流传热的影响，只考虑热传导与热辐射。在COMSOL Multiphysics 中选用固体传热模块与表面对表面辐射模块进行耦合。其控制方程［14］为

式中：ρ为基板密度，kg/m3；Cp为基板的比热容，J/（kg·K）；k为基板导热系数，W/（m·K）；T为基板温度，K；t为传热时间，s；Q为热源，W/m3。

固体表面的换热边界条件为辐射换热，辐射控制方程如下：

式中：ε为基板表面发射率；G为投入基板表面的总辐射，J/kg；J为投入基板表面的有效辐射，J/kg；eb为辐射力，W/m2；ρd为基板表面漫反射率；Gm（J）为净向内辐射通量，W；Gamb为环境投入辐射，J/kg；Gext为外部投入辐射，J/kg；σ为斯蒂芬-玻尔兹曼常数，σ=5.67×10-8W/（m2·K4）；Famb为环境角系数；Tamb为环境温度，K；n为透明介质的折射率，本研究中n取1。

本模型在研究中选用半立方体法求解辐射传热方程。

1.3 边界条件

设定整个计算域的初始温度为35 ℃；为了提高计算效率，将水冷系统简化成恒温壁面，恒定温度设定为25 ℃；设定体积热源Q0，W/m3。

根据镀膜工艺要求，镀制不同种类膜层需要的基板成膜温度不同，因此不同结构参数加热器的输出功率也不同，在优化加热器参数时需要频繁更改输出功率，这种方法优化效率不高。针对该问题，本研究引入PID控制算法与热源Q0耦合。PID控制算法表达式［15］为

式中：t为控制时间，s；Kp为比例系数；Ki为积分系数；Kd为微分系数；Tset为设定温度，K；Tcal为实时检测温度，K。

设定Tset为305 ℃，比例系数Kp=5.08×103，积分系数Ki=35，微分系数Kd=20。温度监测点设置在距离有效加热区内侧顶点弧长R=200 mm处。

选用瞬态求解器，设定求解时间为3 000 s。

1.4 仿真结果

仿真结果如图3～5所示。由图3～5 可知，加热系统在2 000 s 时到达稳态，监测点稳态温度为306.6 ℃，稳态时系统内部高温区域主要集中在加热器、基板及夹具部分。有效加热区内温度沿径向方向由内到外呈现先上升后下降的趋势，距离有效加热区内侧顶点弧长R=188 mm 处到达最高温度，有效加热区外侧顶点为温度最低点，系统有效加热区内最大温差为16.5 ℃。

图3 稳态温度分布云图Fig. 3 The nephogram of steady temperature distribution

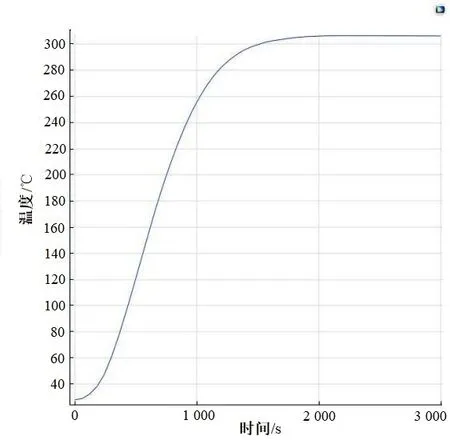
图4 监测点温度随时间变化曲线Fig. 4 Temperature variation curve of monitoring points with time

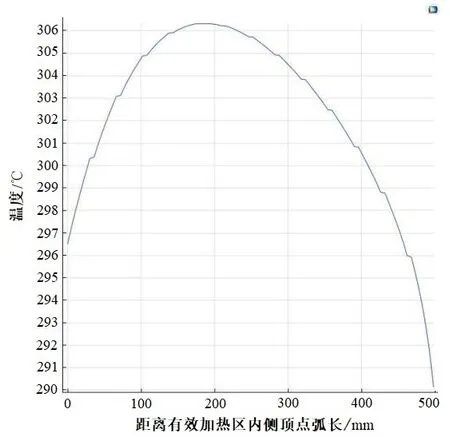
图5 稳态时有效加热区内温度分布曲线Fig. 5 Temperature distribution curve in the effective heating zone during steady state

2 温度影响因素分析

本研究以加热丝排布间距、加热器上侧至基板加热距离以及反射板到辐射板距离为影响因素，通过单一变量法分析各因素对加热系统内基板表面温度均匀性的影响规律。

加热丝按空间位置分为顶部加热丝与侧壁加热丝两部分，加热丝等间隔均匀排布。设定顶部加热丝间隔D1=14 mm，侧壁加热丝间隔D2按D2/D1=k=1.0、1.2、1.3、1.4、1.6 排布，对上述排布方式进行仿真和数据处理，结果如图6 所示。由图6可知，改变顶、侧加热丝的比例对有效加热区内弧长范围125～500 mm 区域影响较大，弧长范围0～125 mm 范围内影响较小。随着k由1 增加至1.6，有效加热区外侧温度大幅降低，有效加热区内侧温度小幅提升。

图6 不同加热丝间隔比例温度分布情况Fig. 6 Temperature distribution of different heating wire spacing ratios

在此研究基础上，本文进行了加热丝总体间隔对温度均匀性的影响研究。取k=1.3，顶加热丝间隔D1分别取12、14、16、18、20 mm 进行仿真和数据处理，结果如图7 所示。由图7 可知，随着加热间隔增加，基板变面平均温度降低，但基板温度受加热丝总体间隔影响较小。

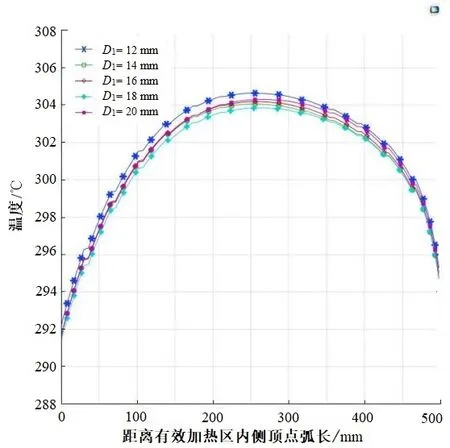
图7 不同总体加热丝间隔温度分布情况Fig. 7 Temperature distribution of different overall heating wire intervals

为了保证镀膜时蒸发源至基板有足够的蒸发距离，加热距离L通常为360～440 mm。L依次取360、380、400、420、440 mm进行仿真分析，结果如图8 所示。由图8 可知，增加加热距离L，有效加热区内总体温度降低，弧长范围0～400 mm 内受影响较大，当加热距离L增加至420 mm 后，温度均匀性改善较小。

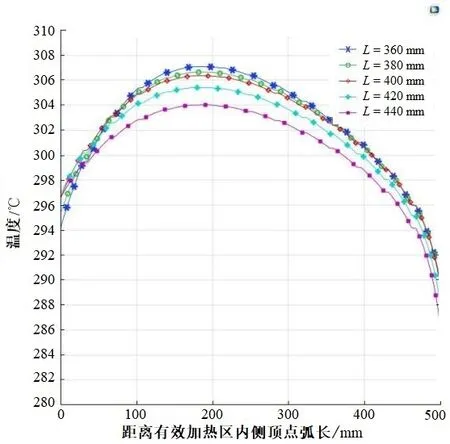
图8 不同加热距离温度分布情况Fig. 8 Temperature distribution of different heating distances

反射板的作用在于隔离辐射板与真空室腔体的热量交换以提升加热系统的加热效率。本研究依次取辐射板与反射板距离D3为2、4、6、8、10 mm 进行仿真分析，结果如图9所示。由图9可知，改变辐射板与反射板的距离，基板整体温度小幅度降低，弧长范围在100～400 mm 内基板温度所受影响较为明显，剩余区域受影响较小，基板整体温度均匀性得到小幅度改善。

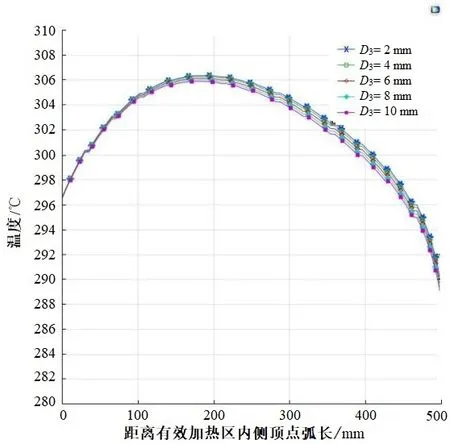
图9 不同反射距离温度分布情况Fig. 9 Temperature distribution of different reflection distances

3 基于Nelder-Mead 单纯形法的加热系统优化

Nelder-Mead 单纯形法是一种不需要求目标函数导数的多参数局部优化算法，单纯形法被广泛用于求解非线性最小值优化问题。其基本思想是指在N维空间中构建一个由N+1个顶点构成的多面体，通过计算得到各个顶点的目标函数值并进行目标函数值排序，选取最大值点为最差点，根据最差点确定优化的下降方向，并根据反射、压缩、收缩、扩张等操作寻找新的顶点来代替最差顶点，最终通过反复迭代使各顶点函数值逐步降低并向目标函数最小值逼近，达到迭代寻优的目的。

本文借助COMSOL 仿真软件中的优化模块对基板加热系统进行优化，选用Nelder-Mead 优化方法进行优化，其步骤如下：

第一步，在基板有效加热区内选取探针目标，分别为最高温度Tmax、最低温度Tmin，设定优化目标函数f（X），设三维变量X（A，B，C），其中A、B、C分别表示顶侧加热丝间距比例k、加热距离L和反射距离D3的值，即优化函数为f（X）=Tmax-Tmin，根据基板表面温度影响性分析确定k、L、D3取值与约束范围，具体参数见表1。

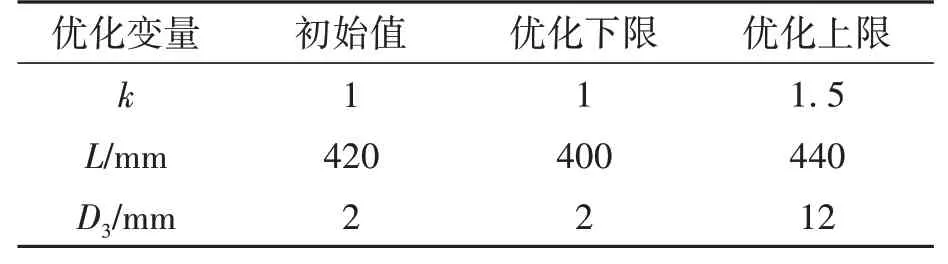
表1 优化变量初始值及约束范围Table 1 Optimization variable initial value and constraint range

第二步，设定初始点X0（A0，B0，C0），A0、B0、C0的值分别取对应变量的初始值，在三维空间内以初始点X0为顶点构造一个具有4 个顶点的单纯形，4个顶点为X0、X1、X2、X3。

第三步，计算对应函数值并对其进行降序排列，其中函数值最大的顶点记为最坏点XH，函数值次大点为XN，函数值最小点记为最好点XL，将去除点XH以外的顶点所构成单纯形的形心记为XZ。

计算反射点XR，其计算公式为

式中：r为反射系数，一般取值为1［16］。

如果f（XL）＜f（XR） ＜f（XN），则令XR为新的XH，输出当前最优函数值及所对应的k、L、D3的值并进行下一次迭代。否则进行扩张或者压缩。

第四步，若f（XL）＞f（XR），即反射点函数值小于当前最小点，则对反射点进行扩张，扩张后的点为扩张点XE，其计算公式为

式中：e为扩张系数，一般取值为2［16］。

如果f（XE） ＜f（XR），则令XE为新的XH；否则令XR为新的XH；返回第三步进行下一次迭代。

第五步，如果f（XR）≥f（XN）并且f（XR）＜f（XH），则令XR为新的XH并进行压缩，否则直接对XH进行压缩，压缩点为XS，其计算公式为

式中：s为压缩系数，一般取值为0.5［16］。

如果f（XS） ＜f（XH），则令XS为新的XH并返回第三步进行下一次迭代。

第六步，如果f（XS）＞f（XH），则认为沿目前方向反射失败，将除最好点XL以外的所有点向XL进行整体收缩，即

式中：X′i为收缩后的第i个顶点；Xi为第i个顶点；g为整体收缩系数，一般取0.5［16］。

计算新收缩点函数值，并返回第三步进行迭代。

第七步，如果||Xi-XL||＜10-3并且|f（Xi） -f（XL）|＜10-3，则停止迭代，并输出最优函数值以及最优函数值所对应的k、L、D3的值。否则返回第三步继续进行迭代。

单纯形优化算法优化变量与函数值结果如图10～12所示。

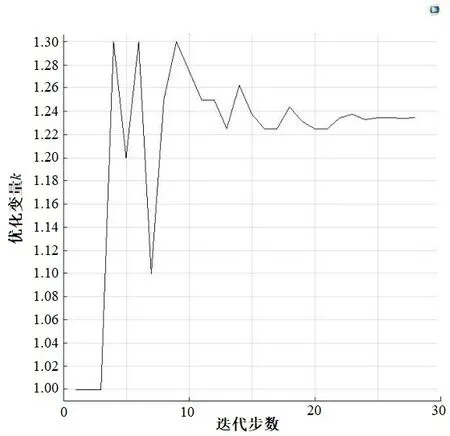
图10 优化变量k迭代曲线Fig. 10 Optimization variable k iteration curve

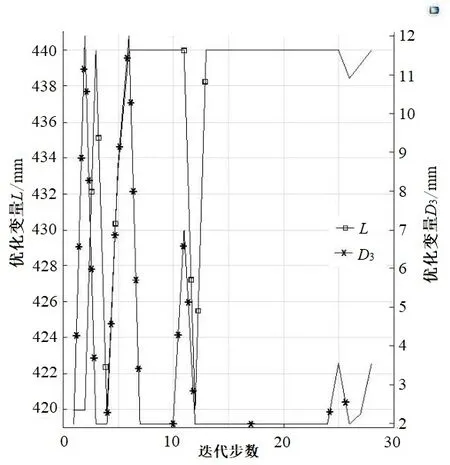
图11 优化变量L、D3迭代曲线Fig. 11 Optimization variable L，D3 iteration curve

图12 目标函数迭代曲线Fig. 12 Objective function iteration curve

在迭代至27次时目标函数满足停止条件，停止时输出函数值为f（X）=9.91 ℃，输出参数组合为k=1.23、L=440 mm、D3=3.56 mm。通过与优化前结果进行对比分析可知，有效加热区内最大温差由16.5 ℃降低至9.91 ℃，证明单纯形法具有较好的优化效果。

4 实验优化验证

为验证加热系统优化效果，本研究中以光驰OTFC-1550 蒸发镀膜机为基础搭建实验平台。实验平台如图13所示，实验平台具体组成见表2。测试基板为φ30 mm 石英片，温度传感器通过高温胶带固定在石英片中心，石英测试片位置如图14 所示。考虑到加热器加工精度问题，对单纯形法优化输出参数组合进行微调，实际加热器参数组合见表3。

表2 基板温度分布测试实验平台组成Table 2 Composition of experimental platform for testing temperature distribution of substrate

表3 加热器结构参数Table 3 Structural parameters of heatermm

图13 基板温度分布测试实验平台Fig.13 Experimental platform for testing substrate temperature distribution

图14 石英测试片放置位置Fig.14 Placement position of quartz test piece

本实验首先关闭腔门进行抽真空，当真空室内压力低于0.1 Pa 开始加热，加热初始温度为室温30 ℃，加热过程中使用PID 程序控制基板温度，设定加热时间为1 h。通过数据采集器对石英片表面温度进行采样，采样周期为60 s。为保证实验重复性，本研究进行两组实验。

加热系统在35 min 时到达稳态，取测试片中心位置即热电偶位置为测试点，为验证仿真结果可靠性，同时取仿真模型相同位置温度数据进行整理。仿真结果与实验结果对比如图15所示。

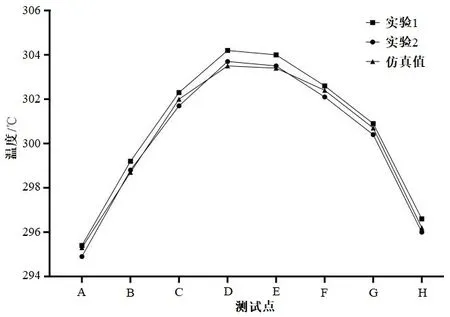
图15 仿真结果与实验结果对比Fig.15 Comparison between simulation results and experimental results

由图15 可知，实验1 测试点平均温度为300.65 ℃，最高温度为304.2 ℃，最低温度为295.4 ℃，测试点最大温差8.8 ℃。实验2 测试点平均温度为300.14 ℃，最高温度303.7 ℃，最低温度为294.9 ℃，最大温差为8.8 ℃。仿真模型测试点平均温度为300.28 ℃，最高温度为303.6 ℃，最低温度为295.3 ℃，最大温差为8.3 ℃。实验与仿真误差为6%，存在误差的主要原因：（1）测试片与基板夹具存在接触热阻；（2）热电偶通过高温胶带固定在测试片上，检测温度受高温胶带影响。

误差在可接受范围内，验证了仿真模型的可靠性与优化效果的有效性，对镀膜机基板加热系统的设计与优化具有一定参考意义。

5 结论

（1）建立了真空加热过程瞬态传热仿真模型，并通过PID 算法实现基板温度精准控制，仿真结果表明有效加热区内温度呈中间区域高两侧区域低的分布规律。

（2）对基板表面温度分布的影响规律进行探究，并借助Nelder-Mead 单纯形法对加热器关键结构参数进行优化设计。基板表面最大温差由16.5 ℃降低至9.91 ℃，温度均匀性显著提升。

（3）通过实验来验证基板表面温度分布情况。实测结果与仿真结果误差为6%，验证了系统优化的有效性，为真空镀膜机基板加热器设计与优化提供参考。