二阶系统根轨迹的完整分析与证明

沈进中，朱洪波，李学洋

（安徽理工大学 电气与信息工程学院，安徽 淮南 232001）

文献［1］第166-167页例4.25“设系统开环传递函数，试绘制其根轨迹并判断闭环系统稳定性。”结论是该系统根轨迹的复数部分是一个圆周；文献［2］第189页习题4～6，证明一个二阶系统根轨迹的复数部分是一个圆周。基于以上二阶系统根轨迹与圆周的联系，笔者经过细致的分析、严格的推导，最终解决所有二阶系统根轨迹的精确绘制问题，并以数学定理的形式展现出来，以便读者理解与运用。

1 二阶系统的根轨迹

二阶系统的开环传递函数的零极点形式有且只有如下3种数学形式。

式中：K∈[0，∞)，为开环系统根轨迹增益。

定理1二阶系统的开环传递函数

中，b、c同时为实数或为一对共轭复数，那么

（1） 如果b、c同时是实数，且b≠c，则系统根轨迹如图1所示；

图1 b、c不相等Fig. 1 b and c are not equal

（2） 如果b、c同时是实数，且b=c，则系统根轨迹如图2所示；

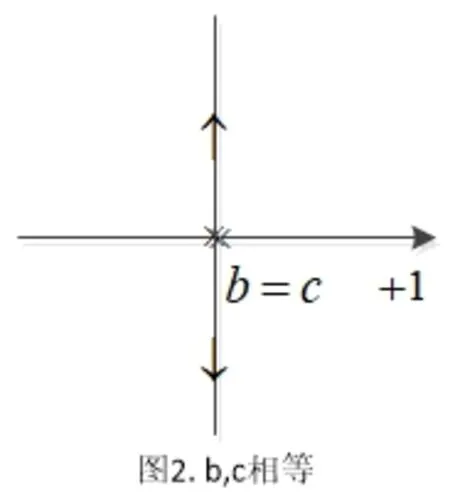
图2 b、c相等Fig. 2 b and c are equal

（3） 如果b、c为一对共轭复数，则系统根轨迹如图3所示。

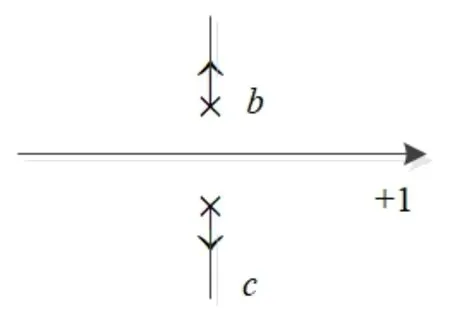
图3 b、c为一对共轭复数Fig. 3 b and c are a pair of conjugate complex numbers

证明：由开环传递函数与闭环特征方程的关系，可得闭环特征方程

它的两个闭环特征根分别为：

容易得出如下结论。

（1） 如果b、c均为实数，且b≠c，那么系统的根轨迹起始于b和c；随着K= 0 →∞，系统的根轨迹如图1所示。

（2） 如果b、c均为实数，且b=c，那么系统的根轨迹起始于b和c，此时系统闭环极点s1=b+；随着K= 0 →∞，系统的根轨迹如图2所示。

（3） 如果b、c为一堆共轭复数，那么系统的根轨迹起始于b和c，此时系统闭环极点为：

随着K= 0 →∞，系统的根轨迹如图3所示。

证毕！

定理2二阶系统的开环传递函数

中，a为实数，b和c同时为实数或为一对共轭复数，那么

（1） 如果b、c同时是实数，且b≠c、a不在b和c之间，则系统根轨迹如图4 所示，根轨迹的复数部分是一个圆周，圆心坐标为（a，0）、半径为；

图4 a不在b、c之间Fig. 4 a is not between b and c

（2） 如果b、c同时是实数，且b≠c、a在b和c之间，则系统根轨迹如图5 所示，根轨迹都在实轴上；

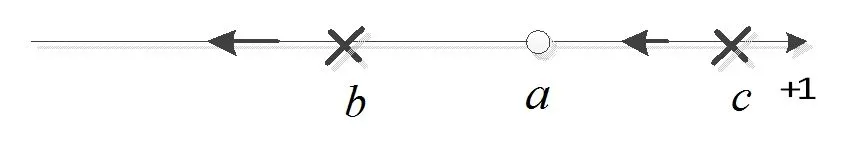
图5 a在b、c之间Fig. 5 a is between b and c

（3） 如果b、c同时是实数，且b=c，则系统根轨迹如图6所示，根轨迹的复数部分是一个圆周，圆心坐标为（a，0）、半径为；

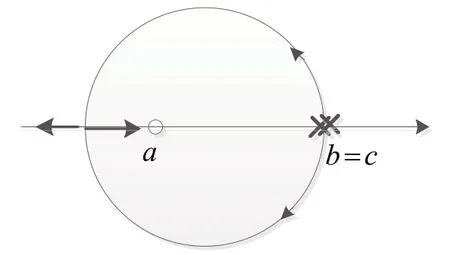
图6 b=cFig. 6 b=c

（4） 如果b、c为一对共轭复数，则系统根轨迹如图7所示，根轨迹的复数部分是圆周的一部分，圆心坐标为（a，0）、半径为。

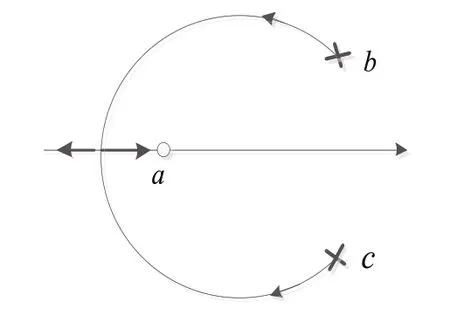
图7 b、c为一对共轭复数Fig. 7 b and c are a pair of conjugate complex numbers

证明：不论b、c为何种情形，只要b+c为实数，b·c必为实数。由开环传递函数的形式，可写出系统闭环特征方程

化简可得

将复数s写成代数式s=x+ jy（y≠0），并代入式(1)，得

化简得

根据实部和虚部均为零，得：

由于y≠0，从而有

根据式（2）、式（4），消去K得

整理得

进一步整理得

因此，当

（1）b、c均为实数，且b≠c、a不在b与c之间时，(a-b) ·(a-c) ＞0。显然s=x+ jy(y≠0)是圆周上的点，且圆周的圆心为（a，0）、半径r=。

根轨迹的实数分离点d满足方程

化简可得

显然，分离点d也是圆周(x-a)2+y2=(a-b)(a-c)上的点。因此，分离点d到开环零点的距离就是该圆周的半径。

（2）b、c均为实数，且b≠c、a在b与c之间时，(a-b) ·(a-c) ＜0。显然，s=x+ jy(y≠0)不是圆周上的点。此时系统根轨迹全落在实数轴上，没有除了实数轴以外的复数部分。

（3）b、c均为实数，且b=c，此时式（5）退化为(x-a)2+y2=(a-b)2＞0（分子分母没有零极点相消），可见根轨迹的复数部分是(x-a)2+y2=(a-b)2＞0的圆周。

（4）b、c为一对共轭复数，即b=σ+ jω、c=σ- jω(ω≠0)，则式（5）变为(x-a)2+y2=a2+bc-a(b+c) =(a-σ)2+ω2＞0，可见根轨迹的复数部分是这个圆周的一部分圆弧（不是整个圆周）。

定理3设二阶系统的开环传递函数（不出现零极点相消），其中a和d同时为实数或一对共轭复数，b和c同时为实数或一对共轭复数，那么系统的根轨迹有如下特点。

（1） 如果b+c≠a+d，那么根轨迹要么全在实数轴上，要么有一部分在实数轴以外，且实数轴以外部分的根轨迹是圆周的一部分或者是整个圆周，如图8所示。

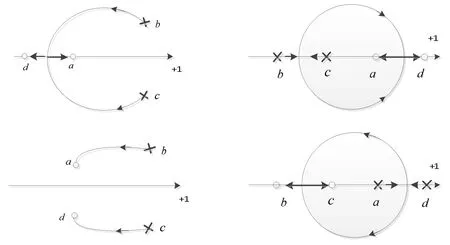
图8 b+c≠a+dFig. 8 b+c≠a+d

（2） 如果b+c=a+d，那么根轨迹要么全在实数轴上，要么有一部分在实数轴以外，且实数轴以外部分的根轨迹是直线x=(a+d)/2 的一部分（非整条直线），如图9所示。

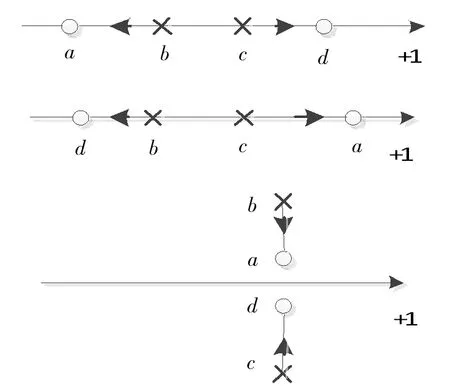
图9 b+c=a+dFig. 9 b+c=a+d

证明：根据开环传递函数与特征方程的关系，可得闭环特征方程

经过化简，得

将s写成复数的形式s=x+ jy（y≠0），并带入式（6），再根据复数等于零的等价条件，即复数的实部、虚部均为零，可得：

由于y≠0，可见s是根轨迹复数部分上的点。

从式（8）可得

将式（9）代入式（7），得

显然，如果

（1）b+c≠a+d，则式（10）表示一个圆周；

（2）b+c=a+d，由式（8）可得K= -1 或者x=(a+d)/2。

将K= -1代入式（7），可得bc=ad，可见集合{b，c}={a，d}。此时，该二阶系统出现零极点相消，与题设相矛盾，因此K≠-1，从而有x=(a+d)/2。此时系统根轨迹的复数部分是直线x=(a+d)/2上的一个部分（不是整个直线）。

证毕！

2 仿真实例

例1 文献［1］第166-167 页的例4.25：设系统开环传递函数，试绘制其根轨迹并分析系统稳定性。

解：根据定理2 的结论（1），可知该系统根轨迹在复平面的部分是一个圆周，圆心为（-1，0）、半径为 0.45。采用MATLAB 软件绘制该系统根轨迹，如图10 所示。由图10 可见，系统根轨迹都在s平面的左半平面。因此，只要Kg＞0，该系统总是稳定的。

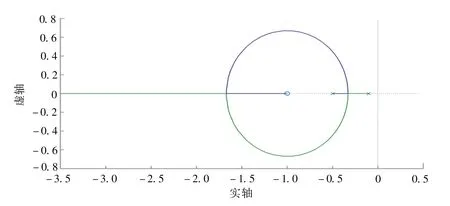
图10 例1中系统的根轨迹Fig.10 The root locus of the system in Example 1

例2 文献［2］第189 页习题4～6：设单位反馈系统的开环传递函数，试从数学上证明复数根轨迹部分是以（-2，0）为圆心、为半径的圆。

证明：分析得知开环极点分别为0和-1、开环零点为-2，由定理2 中的结论（1）可知，该系统根轨迹的复数部分是一个圆，圆心为开环零点（-2，0）、半径为。该系统根轨迹如图11所示。

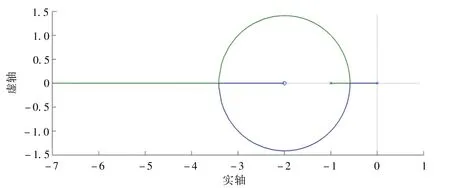
图11 例2中系统的根轨迹Fig.11 The root locus of the system in Example 2

例3 设单位反馈系统的开环传递函数G(s) =，试绘制其根轨迹。

解：这是一个含有两个零点的二阶系统，显然b+c= 2，a+d= -7，b+c≠a+d。由定理3可知，系统根轨迹的复数部分是圆周，在实轴上的分布为[-5，- 2]、[-1，3]。采用MATLAB 软件绘制该系统根轨迹，如图12 所示。由图12 可知，与定理3的结论完全吻合。

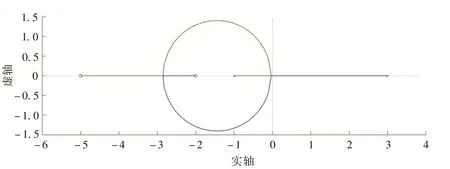
图12 例3中系统的根轨迹Fig. 12 The root locus of the system in Example 3

3 结束语

本文从二阶系统根轨迹的个例出发，通过严格的数学证明，给出了所有二阶系统根轨迹的精确形状。简单地说，就是二阶系统根轨迹的复数部分（如果存在的话），一定是一个完整的圆周或圆周的一部分。

文献［2］第161 页虽然有文字表述定理2 的内容，但并无具体传递函数的表述，也没有任何数学证明，想要准确理解其中的含义比较困难。文献［1-4］分析系统的根轨迹是用相角条件的，绘制的根轨迹都是概略根轨迹，本文则是直接从根轨迹方程出发，得出二阶系统根轨迹的精确形状，处理问题的思路更为直接。对于三阶乃至更高阶的开环传递函数，对应的根轨迹是否有特殊形状，需要将来慢慢探索。