改进VMD-PE的输电线路故障特征提取

谢贤乐,杨 岸

安徽理工大学 电气与信息工程学院,安徽 淮南 232001

1 引 言

三相交流输电线路中,短路故障是很容易发生的,及时的处理对系统的稳定性至关重要,其中常见故障是单相接地短路故障,达总故障概率的80%[1],短时间内及时的切除对国家经济以及系统运行的稳定性都有重要意义。判断过程当中,最重要的就是对故障信号的分解,分解得精细与否直接影响判断的精确性。

发生故障的过程同时也是传递带有故障信号的过程,针对这一故障信号信息,国内外很多学者都在信号分解上做了研究,提出一系列的分解方法,孔垂祥等[2-5]提出了傅里叶级数变换、Haar小波变换、希尔伯特黄变换等;这些方法在一定程度上推进了故障信号的分解,但是这些变换,都是在线路原有数据的基础上进行解耦变换,得到的分量直接进行分解的,对数据的精细度要求比较高;其中,小波函数理论是近几年发展比较迅速的一个分支,小波函数对故障信号进行分解,利用高频对时间的精确进行定位,同时利用波形具有相似性,利用低频进行位置故障定位,但是限制小波函数本身发展的是小波基函数的选取,这很大程度上限制了小波函数的前进,并且在复杂的信号当中,信号的特征向量,求解效果不佳;陶彩霞等[6]利用小波函数为基础,对频域的极大值进行提取,然后构造小波基函数,极大程度上优化了小波基函数的选择,优化了故障信息的频谱混叠现象,但是并未从本质上解决小波基选取的问题,在划分原始故障信号时,频率取值范围以及极大值点的个数无法确定,这影响了经验小波函数的构造;经验模态分解(Empirical Mode Decomposition,EMD)从自身尺度出发,不需要任何基函数,自身带时间尺度,极大程度的提升了分解得精确性,但是容易出现频段叠加效应造成混沌现象,不利于分解信号的区分,姜涛等[7]针对这一问题,根据散热能量理论提出了多元经验模态分解(Multivariate Empirical Mode Decomposition,MEMD),引入映射概念,通过多通道信息在不同空间中形成不同方向的投影,生成多维包络线,减少了混沌发生的概率,测量信号的长度以及测量通道的个数需要人为进行设定,影响后面的分解质量,同时差值进行计算会有一定的误差,所以无法从根本解决分解过程中的端点效应和模态混叠问题。针对以上问题,徐耀松等[8-9]提出的基于变分模态分解方法,利用自适应函数对故障信号进行分解,不需要基函数的选取,增加了分解的精确度,前者的优化算法收敛速度较慢,不利于故障的判断,后者的分解数目以及带宽不确定,影响故障信号的分解的质量。利用熵,将故障中包含的信息提取出来;排列熵[10](permutation entropy,PE)可以不用考虑发生故障时的相位、电阻以及发生的距离,降低了噪声对判断的影响,与近似熵[11](approximate entropy,ApEn)和样本熵[12](sample entropy,SpEn)相比更具优势。

针对以上问题,提出一种基于改进VMD-PE的故障特征提取的方法,利用高斯优化的SVM-PE的分类进行验证,将经过WOA[13]算法优化VMD分解后的IMF,利用PE求熵,得到向量组,作为故障识别的特征向量;利用高斯优化的SVM[13-14]的决策树[15]进行分类,经过MATLAB的验证得到准确率是96.7%。

2 系统原理分析

2.1 VMD原理

VMD的提出主要是解决EMD的混沌问题,核心是把EMD的固有模态模型变成可变换的模型,通过迭代改变成可以对频率以及带宽进行调节来限制的IMF来达到最优。类似于小波函数和傅里叶级数变化的关系,都是将固有不变的问题转化成可变的问题。不同的是,VMD函数不需要基函数的选取,通过频域分解得到不同的谐波信号,目标是求各个模态的带宽之和最小,为了保证分解的准确性,约束条件是,所有模态之和等于原始信号,保证了分解后的信号通过叠加可以得到原始信号。

2.2 排列熵原理

排列熵是对一维信号进行重构的函数,得到新的矩阵,每一行都是一个新的相空间长度序列,设一维时间函数为{X(i),i=1,2,3,…,n},进行k维重构,数学模型如式(1):

(1)

式(1)中:m为嵌入维数,t为延迟时间。

然后对矩阵进行按照升序进行排列,统计每一行下标顺序出现的次数除以m!,作为该行的概率数学模型如式(2):

x(i+(j1-1)t)≤x(i+(j2-1)t)≤…≤x(i+(jm-1)t)

(2)

任意一维向量都可以得到一组唯一的序列,数学模型如式(3):

S(l)={j1,j2,…,jm}

(3)

计算时间序列所有行的信息熵求和即为排列熵。每一行的下标符号序列概率P=1/m!时,排列熵值,记为Hp(m),排列熵值和时间序列的复杂程度成正比。假设S(l)出现的概率是p,排列熵的数学模型如式(4):

(4)

2.3 贝叶斯优化的支持向量机的原理

SVM是一种新型的分类方法,通过使用不同的核函数,把线性不可分的问题转换成可以分类的形式,SVM的核心问题是将不可分的问题,转换成可以分类的问题;SVM的分类的优劣则是取决于超平面到分类点的距离;为了控制好超平面的距离问题,采用贝叶斯网络主动学习的方法,贝叶网络的基本原理就是利用已有的经验,对未知的概率进行预测,适合本文的多个分类的问题。

3 系统改进和优化设计

3.1 基于鲸鱼算法优化改进的VMD

为了得到最优分解的IMF,需要对原始的惩罚参数α以及分级数量K进行权衡,采用鲸鱼算法进行优化,是因为WOA收敛速度快;选择IMF的最小包络熵(Minimun Encelope Entropy,MEE)作为鲸鱼算法的目标函数以及适应度函数来通过寻优达到最解。

最小包络熵的公式简单而且是寻找最小值,比较切合本文的观点,同时是在鲸鱼算法中提出来的,用在鲸鱼算法的寻求最优参数最合适不过了,以目标是求各个模态的带宽之和最小为目标,IMF是本文的目标的表达方式,切合极小值包络熵的输入参数,所以用其做目标函数最为合适了,数学模型如下:

{α,I}=argmin{Eb1,Eb2Eb3…EbI}

其中,aij是能量算子的子模型的包络信号,bij是aij归一化的结果,Ebi表示包熵,N表示节点个数,I表示IMF的个数。

鲸鱼算法是启发式优化算法,模拟生物界座头鲸鱼泡泡网特殊的捕食行为方式,算法主要有3个阶段:包围猎物、泡泡网攻击、搜寻猎物。本文是以最目标函数的最小值为适应度函数的,所以函数值越小,算法就越好,鲸鱼算法收敛速度快,并且算法调整的参数少,不容易陷入局部最优的特点,适合做大数据算法的搜索,同时电力系统的数据就是大数据集合体,所以采用鲸鱼算法可以更快地求出电力系统故障的位置,适合电力系统的大数据以及迅速切除故障的特点。

将[K,α]转换为求解坐标的问题,求各个IMF的最小包络熵为目标,利用鲸鱼算法进行收敛求得最后的目标位置。

WOA算法在优化VMD时,开始的便是假定当前的坐标位置便是包络熵最小的的位置或者是使VMD得分解接近最优的分解的位置。利用其他代理搜索去跟新新的位置,与之前的位置进行比较,选择出在这几个当中包络熵值最小的位置,以此位置作为开始最优的位置,重复之前的步骤。

以最小包络熵的值为目标函数时,求解最小包络熵的位置,在与前者比较得到最小熵值之后,防止局部陷入最优的问题。在包围最小包络熵时,采用收缩环绕机制和螺旋环绕模型进行位置的更新与比较。以概率为50%来更新新的鲸鱼位置坐标,并计算最小包络熵的值与之前的值进行比较,选出最小的值作为当前的最优位置。

选择在包围之后进行泡沫攻击,来选择最小的包络熵值,为了更好地显示出局部的开发能力,利用随机数的方法进行位置的更新,产生的目标结果值在范围之内时,用泡沫攻击的方式去选择最小包络熵的值为最新的位置;如果目标值不在范围之内,为了增加全局搜索的能力,需要寻找新的目标值猎物,采用远离这个目前最优位置的方式进行增加全局搜索能力和勘探功能。

通过最小包络熵值为目标函数以及鲸鱼算法的优化,既防止了陷入局部最优解的问题以及陷入死循环的问题,同时也保证了VMD的分解最合适的作用,在WOA算法以及最小包络熵为目标函数的优化下,各个模态的带宽之和最小,保证了分解的精度以及为接下来的分类判断提供了强有力的理论支撑。

下面是算法流程:

(1) 选择最小包络熵作为目标函数,并确定目标函数其他值的范围。

(2) 将待求参数α、K构成位置向量[K,α],作为位置向量。

(3) 将位置向量[K,α]代入VMD中,记录包络熵的大小,计算出适应值。

(4) 与之前的位置相比较,适应度的值是否变小。

(5) 如若不是重回步骤(3)直到达到最优解。

算法流程图如图1所示:

图1 WOA优化VMDFig.1 WOA optimizing VMD

3.2 决策树的优化

SVM是二分类的方法,单只用SVM很难对多个故障进行分类;决策树是一种监督学习的方法,顾名思义决策树是一种树形结构,通过节点往下进行分类,当类别过多时,会出现分类不准确的情况,但是结合决策的节点和SVM,并且利用高斯优化SVM结合决策树可以让分类更加的多且更加准确。

利用优化后的SVM结合决策树,采用二叉树的组合策略,在分类当中先挑选出第一类,然后将剩下的作为另一类,在决策点处利用“1-a-r”的方法进行分类,只到所有的类别都被分解完成,所产生的叶子节点便是每个分类的结果,提升了分类的准确率,同时也提升了分类的效率。分类流程图如图2所示。

图2 决策树分类流程图Fig.2 Flowchart of decision tree classification

4 仿真验证

4.1 仿真参数设置

仿真采用MATLB软件,在Simulink中搭建模拟10 kV模拟生成短路故障的数据集,其简化参数设置如下所示。

设置参数如下:供电电源为20 kV,变压器的变比2∶1,线路长度设置330 km,线路的正序参数R1=3.648*10-2Ω/km,L1=1.348 mH/km,C1=8.68*10-3μF/km,零序参数R0=0.3 Ω/km,L0=3.69 mH/km,C0=6.166*10-3μF/km,仿真时间设置0.5 s,短路开始时间统一设置在0.3 s开始出现故障,保证线路数据的统一性。

同时为了证明实验结果分类的多样性,采用多个变量的方法作为实验数据的产生,同组数据只保证一个变量,进行多组数据的组合。此次仿真模拟选用四种比较典型的故障短路类型,单相接地短路(Ag)、双相短路(AB)、双相接地短路(ABg)、三相短路(ABC)。设置6个初始故障角每次增加60 °,分别为0 °、60 °、120 °、180 °、240 °、300 °。故障位置依次增加30 km,总共设置10个故障位置,过渡电阻选择10 Ω、100 Ω以及300 Ω,提取短路时刻三相电压作为数据分析的依据,共获得数据样本4×6×10×3=720种。

实验电路简图如图3所示。

图3 10 kV模拟故障简电路图Fig. 3 Simple circuit diagram of 10 kV simulated fault

4.2 实验结果分析

WOA对VMD优化,通过仿真可以得知,最优综合指标是5.917 8e-4,鲸鱼在第7代迭代停止,迭代曲线如图4所示,最终得到的优化参数[α,Κ]=(619,5),由迭代曲线图可以证明前文所述的鲸鱼算法收敛速度快的特点。将迭代数据的结果带入VMD当中,进行故障电压的分解进行验证,得到最优的各个模态带宽最小和,为了验证VMD分解混沌性的减小,特选用EMD以及VMD的频谱图作为验证的依据。由于篇幅问题,选用A相接地的故障电压进行展示。

不管是从信号分解图(图5、图6)上来看,还是从频谱幅值的信息图(图7、图8)来看,从分解图上来看,EMD的分解IMF3、IMF4、IMF5所含的信息减少,从后面的频谱幅值也可以看出EMD分解的频谱幅值近乎没有区别;相较于EMD的分解,VMD的特征区别明显,分解曲线上看各个差异性比较大,同时从频谱幅值上来开,各个IMF的区别比较大,所以由此得到结论,VMD分解的优越性,远远高于EMD,所以选择VMD结和PE,求其特征向量组,就可以得到两者区分度比较高的特征信号。

图4 WOA优化SVM的收敛曲线Fig.4 Convergence curve of WOA optimizing SVM

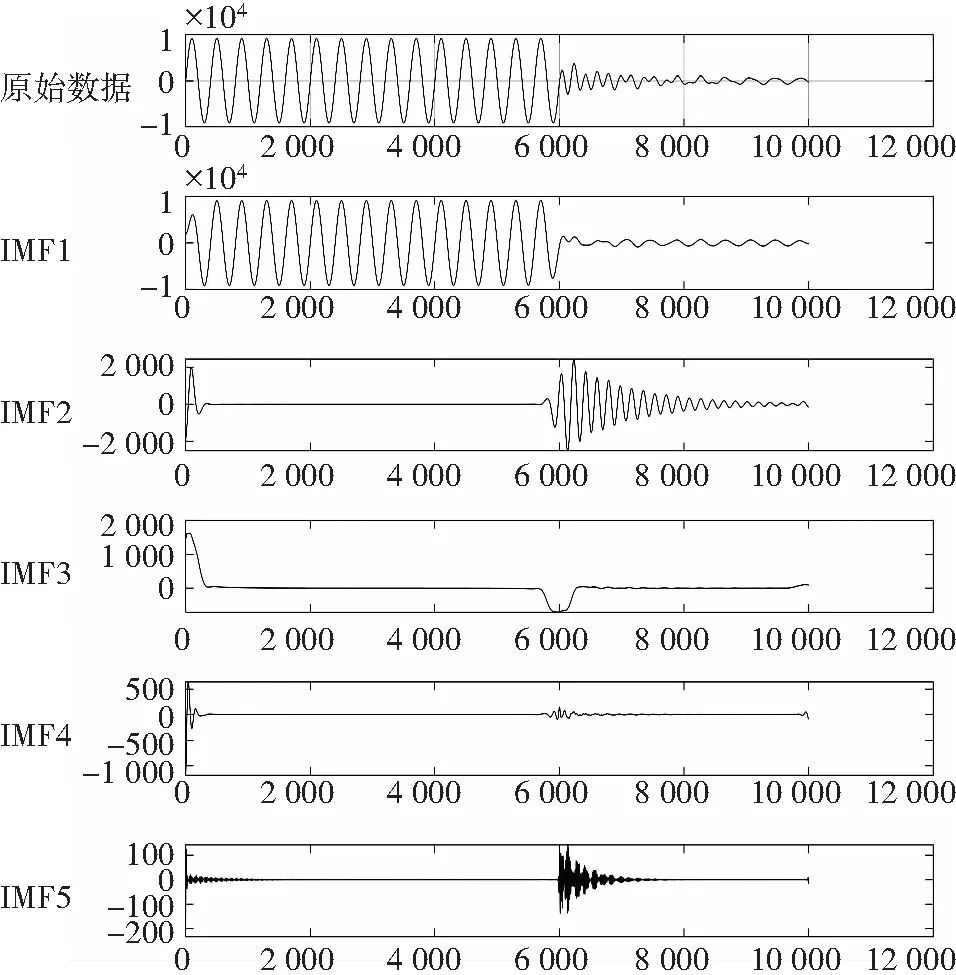
图5 VMD分解得到5个IMFFig.5 Five IMFs obtained by VMD decomposition

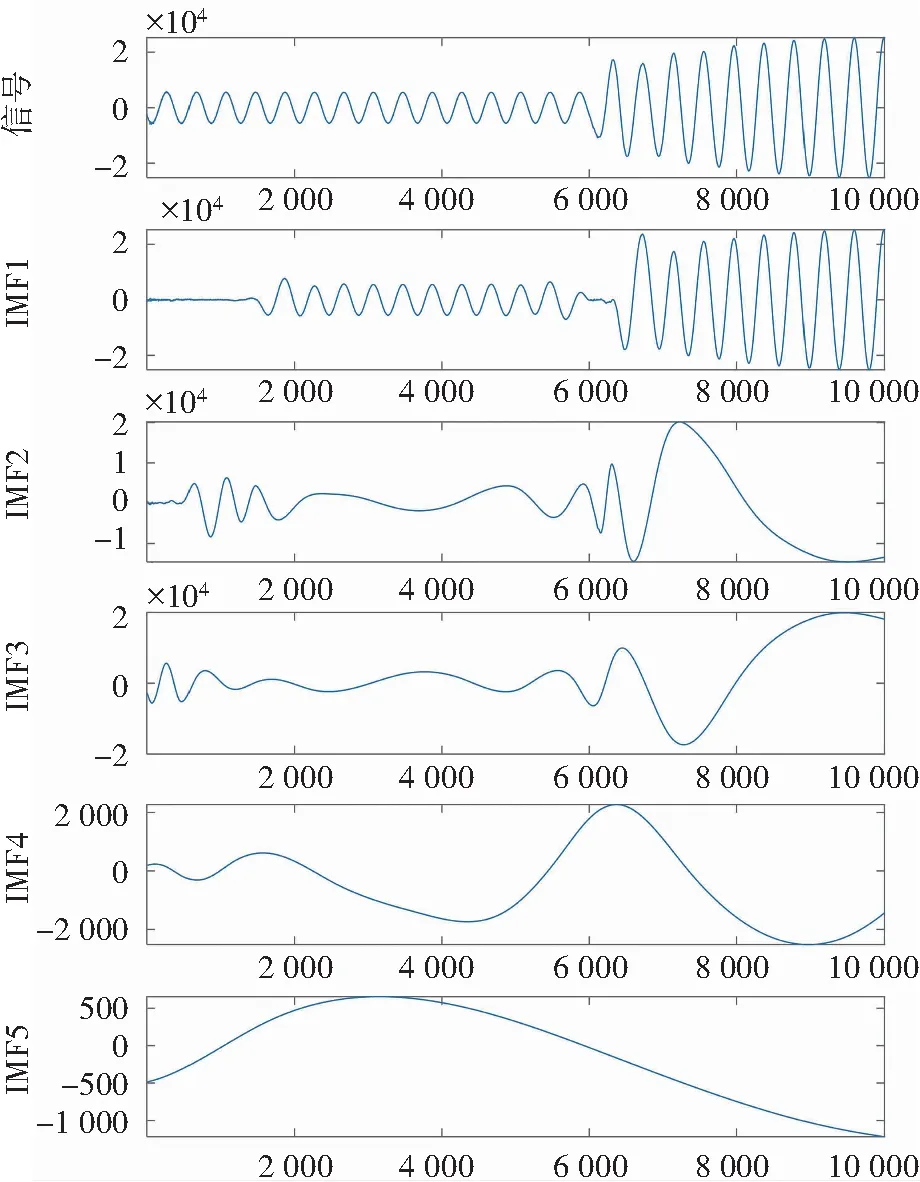
图6 EMD分解得到5个IMFFig.6 Five IMFs obtained by EMD decomposition

图7 VMD处理后的频谱Fig.7 Spectrum after VMD processing

图8 EMD处理后的频谱Fig.8 Spectrum after EMD processing

为了证明分解的有效性,下面分别是Ag、ABg、AB、ABC 4种比较特殊的短路情况下的VMD分解后的排列熵。选择故障角为0°,短路接地电阻是10 Ω,故障点在150 km处的4种故障作为结果展示。如表1所示。

表1 VMD分解后的各个IMF的排列熵的值Table 1 Permutation entropy values of each IMF after VMD decomposition

表1是故障发生后,经过IMF分解后,求得的各个IMF的排列熵,从表1可以看出,4个不同的故障,人眼很难发现其中的规律。但是可以看到的是各个熵的差值比较明显,以及结合下面的频谱图可以很好地说明,VMD-PE可以作为特征向量值作为判断的依据。

同组排列熵的熵值的不同以及异组的差异性,证明排列熵构成的向量组含有信息量,可以进行下一步的验证。

4.3 SVM-DT分类

对于熵提取后的数据,虽具有了一定的信息性,但是并不能直接分辨出来,利用支持向量机进行处理,但是支持向量机的主要作用是为了区分二分面,加入决策树进行多分类;为了更好地利用SVM,防止过拟合,加入高斯函数优化SVM;分别将VMD-PE以及EMD-PE的数据代入分类算法当中进行验证。

其中1代表Ag短路,2代表ABg短路,3代表AB短路,4代表ABC短路。其验证结果如图9、图10所示。

图9 VMD-PE的预测准确率的散点图Fig.9 Scatter plot of prediction accuracy of VMD-PE

图10 VMD-PE的各个分类的预测准确率Fig.10 Prediction accuracy of each VMD-PE classification

同时得到表2。

表2 VMD-MSE与EMD-MSE识别准确率上的比较Table 2 Comparison of recognition accuracy between VMD-MSE and EMD-MSE

显而易见,不管是从分解后的频谱幅值上来看,还是从分类的结果上来看,改进的VMD-PE都优于EMD-PE,并且,单独看改进的VMD-PE总的准确率,高达96.7%,也满足使用的要求,可以有效地识别故障类型;分别看每种故障类型,每种的准确率也都优越于EMD-PE。

5 结 论

基于鲸鱼算法改进了VMD,利用改进后的VMD结合排列熵构成向量组,通分类算法的验证仿真以及证明,得到结论:

(1) 鲸鱼算法优化VMD,得到本征模态的分解个数以及惩罚参数,提高了分解的准确度。

(2) 利用VMD结合PE,将故障电压信号可以分解成特征向量,作为分类算法数据来源的依据。

(3) 排列熵可以反映一定的信息情况,且只与复杂程度有关,和时间无关,并且排列熵是自适应函数,不需要基函数,增加了分解的准确性。

(4) 利用改进的VMD-PE提取特征向量结合高斯优化的SVM-DT,可以将二分类问题转化成多分类问题,并且相较于EMD-PE提取特征向量的方法,准确率更高,说明了VMD-PE此方法的优越性。