两集合并集可测和原集合自身可测的关系
林鑫宇, 李文娟
(1.西北工业大学 教育实验学院,西安 710129; 2.西北工业大学 数学与统计学院,西安 710129)
1 问题产生
实变函数是一门重要的数学专业课,抽象性高,学习难度大.反例的研究可以帮助更好的理解定义和定理.有鉴于此,国内许多学者对实变函数的反例研究已有了不少成果[1-2].
可测函数和Lebesgue积分是实变函数中的重要概念.教材[3]中提到为了构造Lebesgue积分,要求函数f(x)满足:∀a,b∈,E={x∈n;a≤f(x)≤b}是可测的;而可测函数的定义却要求函数f(x)满足:∀a∈,E={x∈n;f(x)≥a}是可测的.这两个条件是否等价呢?显然前者是后者的必要条件,那么前者是否还是后者的充分条件呢?下面尝试由前者推出后者.
设f(x)是定义在可测集E上的函数,满足∀a,b∈,Eab∶={x∈n;a≤f(x)≤b}可测.此时,可证∀a∈,n;a≤f(x)<+∞}可测,所以要证明∀a∈,Ea={x∈n;f(x)≥a}可测,只要证明E+∶={x∈n;f(x)=+∞}可测.考虑到集合E*∶={x∈n;-∞ 定义1[4]设集合E⊂n.若对任意的点集T⊂n,有 m*(T)=m*(T∩E)+m*(T∩Ec), 则称集合E是Lebesgue可测的. 定义2设集合A,B⊂n,若∃开集VA⊃A,开集VB⊃B,使得VA∩VB=∅,则称A,B是隔离的. 定理1下列三个命题是等价的: (i)A,B是隔离的; (ii)A∩B=∂B∩A=∂A∩B=∅,其中∂A表示集合A的边界; 证(i)推(ii) 因为A,B是隔离的,所以∃开集GA⊃A,开集GB⊃B,使得 GA∩GB=∅. (1) A∩B=∅是显然的. 事实上,还有∂B∩A=∅,不然,∃t∈∂B∩A.现任取开集VA⊃A,开集VB⊃B.因为t∈∂B∩A⊂A⊂VA及VA是开集,所以∃δ>0,使N(t,δ)⊂VA,从而VA∩VB⊃N(t,δ)∩B.又因为t∈∂B∩A⊂∂B,所以对上述δ>0,N(t,δ)∩B≠∅,因此VA∩VB≠∅.考虑到VA,VB具有任意性,这与(1)矛盾. 同理,∂A∩B=∅. 同理,对∀y∈B,∃δy>0,使 N(y,δy)∩A=∅. (2) 从而x0∈N(y0,δy0)∩A,这与(2)矛盾. 这样,就找到了开集GA⊃A,开集GB⊃B,满足GA∩GB=∅,所以A,B是隔离的. 设集合A,B⊂n,已知A∪B可测(大前提),现在在不同条件下研究A,B各自的可测性. 此时,A,B各自的可测性是无法确定的,有4种可能的情况,即(A的可测性,B的可测性)为(可测,可测)或(可测,不可测)或(不可测,可测)或(不可测,不可测).可以举例说明. 不妨取A∪B=[0,3].设S1是[0,1]上的不可测集,S2是[2,3]上的不可测集.下面给出每种A,B不同的可测性组合下A,B的一种可能取值. (可测,可测):A=[2,3],B=[0,2]; (可测,不可测):A=[0,3],B=S2∪[0,1]; (不可测,可测):A=S1∪[2,3],B=[0,3]; (不可测,不可测):A=S1∪[2,3],B=S2∪[0,2]. 此时,A,B的可测性一定是相同的.不然A,B一个可测,另一个不可测.不妨设A可测,B不可测.由于A∩B=∅,且A及A∪B可测,有B=(A∪B)A可测,这便与B不可测矛盾了.所以此时只有两种情况,即(A的可测性,B的可测性)为(可测,可测)或(不可测,不可测).可以举例说明. 不妨取A∪B=[0,3].设S是[0,1]上的不可测集.下面给出每种A,B不同的可测性组合下A,B的一种可能取值. (可测,可测):A=[2,3],B=[0,2);A∩B=∅; (不可测,不可测):A=S,B=[0,3]S;A∩B=∅. 由3.1和3.2可以发现,在加上一些限制条件之后,A,B的可测性组合也随之更确定.不过即使在A∩B=∅的条件下,也无法由A∪B可测得到A,B均可测.这说明条件“A∩B=∅”有一点弱.根据定理1,下面试试一个更强的条件. 此时,A,B均可测,下面给出证明. 定理2若A⊂n不可测,则对∀B⊂n,只要A,B是隔离的,那么A∪B不可测. 证假设A∪B可测,则对∀ε>0,∃开集G⊃A∪B,使得m*(G(A∪B))<ε. 因为A,B是隔离的,所以∃开集VA⊃A,VB⊃B,满足VA∩VB=∅.令 GA=VA∩G,GB=VB∩G, 则有 GAA⊂(GAA)∪(GBB)⊂G(A∪B), 所以 m*(GAA)≤m*(G(A∪B))<ε. 这说明A可测,与题设矛盾.故假设不成立,即A∪B不可测. 推论1若A∪B可测,且A,B是隔离的,那么A,B均可测. 至此,在A∪B可测的大前提下,得到如下A,B均可测的充分条件:A,B是隔离的.不过在A∪B可测的大前提下,即使A,B均可测,A,B也不一定是隔离的.例子很容易找到.例如,A∪B=[0,3],A=[0,3],B=[1,2]. 这就是说,在A∪B可测的大前提下,“A,B是隔离的”只是“A,B均可测”的充分不必要条件,换句话说,这个条件太强了,那么能否找到一个更弱的条件呢? 为找到充要条件,需要逐步减弱条件.由定理1知,“A,B是隔离的”可以转换成“A∩B=∂B∩A=∂A∩B=∅”三个条件.因为A∩B=∅是很好的性质,所以选择先保留这个条件,减弱其他两个条件.那么减弱之后∂B∩A和∂A∩B中应至少有一个不为空集,而这就成为隔离条件失效的关键因素.于是提出如下猜想: 猜想1设A∪B可测,A∩B=∅,∂B∩A和∂A∩B均可测.将他们分别从A,B上去掉后,如果剩下的两个集合满足隔离条件,那么A,B均可测. 验证猜想1的第一步是从A,B上分别去掉各自的一个可测子集,并保证剩下两个集合满足隔离条件,检验此时A,B是否均可测. 定理3设A∪B可测,A∩B=∅,A*,B*分别是A,B的可测子集,若AA*,BB*是隔离的,则A,B均可测. 证由A∩B=∅及A*,B*分别是A,B的子集可得 (A∪B)A*B*=(AA*)∪(BB*). 因为A∪B,A*及B*均可测,所以 (AA*)∪(BB*)=(A∪B)A*B* 可测.又因为AA*,BB*是隔离,由推论1知,AA*,BB*均可测,所以A=(AA*)∪A*可测.同理,B可测. 接下来证明两个辅助结论. 引理1设集合B⊂A⊂n,若AB⊂∂A,则∂B⊂∂A. 证任取x∈∂B,要证:x∈∂A,只需证:对∀ε>0,N(x,ε)∩A≠∅且N(x,ε)∩Ac≠∅. 现任取ε>0,因为x∈∂B,所以∃y∈N(x,ε)∩B,∃z∈N(x,ε)∩Bc⊂Bc.于是y∈N(x,ε)∩B⊂N(x,ε)∩A,这说明N(x,ε)∩A≠∅. 下证:N(x,ε)∩Ac≠∅.分两类讨论. (i)z∈AB. 因为z∈AB⊂∂A,所以对于ε′=ε-ρ(x,z)>0, ∃z′∈N(z,ε′)∩Ac⊂Ac,由于 ρ(z′,x)≤ρ(x,z)+ρ(z′,z)<ρ(x,z)+ε-ρ(x,z)=ε, 故z′∈N(x,ε),从而z′∈N(x,ε)∩Ac,所以N(x,ε)∩Ac≠∅. (ii)z∉AB. 此时,考虑到z∈Bc,有z∉A,所以z∈N(x,ε)∩Ac,于是N(x,ε)∩Ac≠∅. 综上,对上述ε>0,N(x,ε)∩A≠∅且N(x,ε)∩Ac≠∅,由ε的任意性,得x∈∂A.再由x的任意性知,∂B⊂∂A. 引理2若A∩B=∅,则A°∩∂B=∅. 证假设A°∩∂B≠∅,那么∃z∈A°∩∂B⊂A°,所以∃δ>0,使N(z,δ)⊂A,从而A∩B⊃N(z,δ)∩B.又因为z∈A°∩∂B⊂∂B,所以N(z,δ)∩B≠∅,从而A∩B≠∅,这与题设中的A∩B=∅矛盾,故假设不成立,即A°∩∂B=∅. 最后将从A,B上去掉的两个子集换成具体的∂B∩A和∂A∩B,再利用以上两个辅助定理,证明猜想1. 定理4设A∪B可测,A∩B=∅,若A∩∂B,B∩∂A均可测,则A,B均可测. 证记A*∶=A∩∂B,B*∶=B∩∂A,则A*,B*分别是A,B的可测子集.由A∩B=∅及引理2知,A°∩∂B=∅,于是 A*=A∩∂B⊂(A°∩∂B)∪(∂A∩∂B)=∂A∩∂B⊂∂A, 从而A(AA*)=A*⊂∂A,由引理1知,∂(AA*)⊂∂A. 因为 (BB*)∩∂A=(B∂A)∩∂A=∅, 所以 (BB*)∩∂(AA*)⊂(BB*)∩∂A=∅, 从而 (BB*)∩∂(AA*)=∅. 同理,(AA*)∩∂(BB*)=∅. 又因为(AA*)∩(BB*)=∅,由定理1知,AA*,BB*是隔离的.又因为A∪B可测,A∩B=∅,A*,B*分别是A,B的可测子集,由定理3知,A,B均可测. 上面的研究一直保留了A∩B=∅的条件,现在将这个条件减弱为A∩B可测,并由定理4的启发得到了定理5. 定理5A,B均可测的充要条件是A∪B,A∩B,A∩∂(BA),(BA)∩∂A均可测. 证必要性显然成立. 充分性.记A*∶=A,B*∶=BA,则A*∪B*=A∪(BA)=A∪B可测;A*∩B*=A∩(BA)=∅;A*∩∂B*=A∩∂(BA)可测;B*∩∂A*=(BA)∩∂A可测,由定理4知,A*,B*均可测,所以A=A*可测,B=(B∩A)∪(BA)=(A∩B)∪B*可测. 推论2若A∪B可测,则A,B均可测的充要条件是A∩B,A∩∂(BA),(BA)∩∂A均可测. 至此,得到了在A∪B可测的大前提下,A,B均可测的充要条件. 定理5给出了A,B均可测条件的一种等价刻画.它还有另一个版本:A,B均可测的充要条件是A∪B,A∩B,A∩(BA)′,(BA)∩A′均可测,其中A′表示集合A的导集. 下面给出定理5的一些应用. 例1设S1是[0,1]上的任意一个不可测集合,S2=[0,1]S1,求证:S1∩S′2和S2∩S′1至少有一个不可测. 证假设S1∩S′2和S2∩S′1均可测.因为S1∪S2=[0,1]可测,且S1∩S2=∅可测,由定理5知,S1,S2均可测,这与题设矛盾,故假设不成立,即S1∩S′2和S2∩S′1至少有一个不可测. 在本例中,由于S1和S2都是抽象的集合,从正面证明十分困难,不过通过反证法,可以由定理5很好地解决. 例2定义在可测集E⊂n上的函数f(x)满足:∀x,y∈E,若‖x‖≤‖y‖,则f(x)≤f(y),其中,求证:f(x)是E上的可测函数. 证任取a∈,记 下面分两类讨论. 故 文中给出了两集合分别可测的另一种等价刻画,这个刻画可以使我们更清楚地看到 “A,B均可测”是比“A∪B可测”要强得多的条件,在一般情况下,后者的成立是无法保证前者的成立的.这也否定了一开始的猜测,即“(广义实值)函数f(x)满足:∀a,b∈,E={x∈n;a≤f(x)≤b}是可测的”和“(广义实值)函数f(x)满足:∀a∈,E={x∈n;f(x)≥a}是可测的”两者是不等价的. 致谢作者非常感谢西北工业大学数学与统计学院李文娟副教授的有益讨论,同时感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.2 预备知识
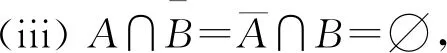
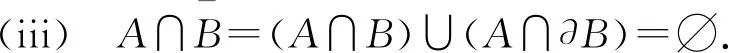
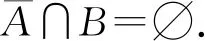
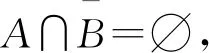

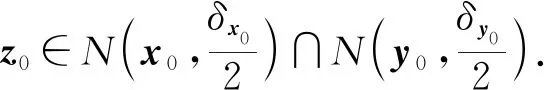
3 主要结果
3.1 无附加条件
3.2 加上限制条件:A∩B=∅
3.3 加上限制条件:A,B是隔离的
3.4 探寻充要条件
4 应 用
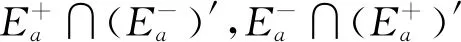
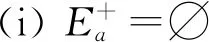
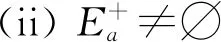
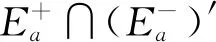
5 结 论

