非线性椭圆型方程组边值问题的可解性
李殷杰, 钟金标
(安庆师范大学 数理学院,安徽 安庆 246133)
0 引 言
源于物理,力学等方面的很多问题,可通过建立椭圆型方程或方程组边值问题来给予解决,从而这方面的研究一直是偏微分方程研究领域的热点之一,在本文研究下列椭圆型方程组Dirichlet边值问题
(1)
的可解性,这里Ω⊂n为有界光滑区域,目前,对椭圆型方程和方程组边值问题正解的存在性,唯一性或多解性的研究非常活跃,例如文献[1-4]是近期发表的研究文章.
文献[1]中研究了半线性椭圆型方程组
(2)
其中Ω为n中有界光滑区域,非线性项f(x,u),g(x,v)满足条件:


(A3) 对x∈Ω,f(x,s),g(x,s)关于s是严格递增的.
利用不动点定理证明了问题(2)正解的存在性,并讨论了解的唯一性,这里f,g满足条件(A2),说明f(x,s),g(x,s)在+∞处关于s只能是次线性和线性的,对f(x,s),g(x,s)在+∞处关于s是超线性的情形,问题(1)是否存在正解未给予证明.
在文献[2]中利用Morse理论研究了问题
(3)
非平凡解的存在性,证明了非平凡弱解的存在性定理.
在文献[3]中讨论下列椭圆型方程边值问题
这里Ω⊂2是有界连通的光滑域,0 该问题中非线性项关于u是次线性的,证明了经典解的存在性,文献[4-7]也是近期发表的相关文章. 设问题(1)中的非线性项满足下列条件: (H3)f(x,0,0),g(x,0,0)中至少有一个大于0. 定理1若条件(H1)成立,则问题(1)只能存在非负解. 证由条件(H1)可知f(x,u,v)≥0,g(x,u,v)≥0,从而 由上调和函数极值原理[8]知u≥0,v≥0,从而问题(1)只能存在非负解. 证由定理1知,问题(1)只能存在非负解,做函数集合 显然D为C2(Ω)×C2(Ω)中闭凸子集,取(s(x),t(x))∈D,让u,v分别是问题 (6) (7) 从而 做算子T如下:T∶(s,t)=(u,v).即 因为L=(-Δ)-1为紧正算子[10],f,g为非负连续函数,T为D映射到D的紧正算子,由Schauder不动点定理[8],T有一个不动点,该不动点即为问题(1)的非负解. 下面考察带参数的椭圆型方程组边值问题 (8) 其中Ω为n中有界光滑区域,λ>0,μ>0为正参数,利用定理2结论,可以得出. 定理3当λ,μ充分小时,且f(x,s,t),g(x,s,t)满足条件(H1),(H2),(H3)时,问题(8)存在有界正解. -Δu-λf(x,u,v)=-λf(x,0,0)≤0, -Δv-gf(x,u,v)=-μg(x,0,0)≤0, 当λ,μ充分小时, 利用定理2的结论知,问题(8)存在有界正解. 注 在文献[1]中对所研究的问题,其非线性项在+∞处含线性与次线性部分,证明了正解的存在,而对超线性情形正解是否存在解未给予证明,而在研究问题(8)中,非线性函数f,g在+∞处可以是超线性的,根据定理3仍可得到问题(8)存在有界正解. 而对线性项为超线性情形时,一直是此类问题研究的的难点之一. 应用实例:考察问题 (9) 这里Ω为n中有界光滑区域.f(x,s,t)=1+(s+t)2,g(x,s,t)=2+(s+t)4,显然满足条件(H1),(H2),(H3). 由定理3可知,当λ,μ充分小时,问题(9)存在有界正解,这里f,g在+∞处是超线性的. 本文首先研究了半线性方程组(1)正解的存在性,其中非线性项f(x,u,v),g(x,u,v)为超线性函数.利用上,下解方法及不动点定理证明了正解的存在性,对f(x,u,v),g(x,u,v)为超线性函数情形,相关研究中f(x,u,v),g(x,u,v)都是较为特殊的函数.本文通过引入小参数,对f(x,u,v),g(x,u,v)为较为一般的超线性函数,证明了带参数的椭圆型方程组边值问题(8)存在有界正解,并给出了应用实例. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.


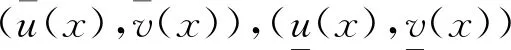
1 主要结论





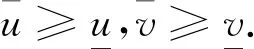
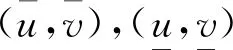
2 结 论

