500 kV 防风偏复合绝缘子理论及仿真分析
陈俊 翁兰溪 林锐
(中国电建集团福建省电力勘测设计院有限公司 福建福州 350003)
0 引言
福建省风灾事故调查表明,跳线对塔身风偏跳闸事故是最常见的风灾事故之一。台风具有虹吸效应和脉动性,容易导致跳线串或软跳线部分上扬,空气中积累的大量水分使空气击穿电压降低,增加了风偏闪络发生的可能性。
台风多发区的220 kV 及以下线路转角塔跳线采用防风偏绝缘子后,显著降低跳线风偏位移,从而减少跳闸事故。但是沿海台风地区500 kV 线路基本风速大、跳线串及引流线较长、分裂数多,复合绝缘子底座弯距远大于220 kV 及以下线路,制约了防风偏复合绝缘子在500 kV 线路上的应用。
500 kV 线路若采用变径结构的防风偏复合绝缘子,可有效降低绝缘子底座对挂线角钢的附加扭矩,扩大了防风偏复合绝缘子的适用范围。但是对于变径结构的尺寸设计尚不明确,本文针对等径及变径防风偏复合绝缘子的力学特性进行仿真分析,并探讨各物理参数对变形及应力的影响程度。
1 变径防风偏复合绝缘子结构
防风偏绝缘子如采用整体等径的芯棒结构,因其自身需要承受较大的弯矩,要求其整体刚性强、重量大、截面大。由于防风偏绝缘子一端为悬垂端,用于连接导线,因其迎风面积大,从而使其受风力荷载也大。防风偏绝缘子的另一端直接固定在横担上,整体刚性且重量大的绝缘子在多次受风力冲击而扭曲弹性形变后,固定连接处的连接螺栓和横担角钢在大弯距作用下容易发生破坏或失稳。
为保证绝缘子在弯曲负荷下的偏移量能够满足安全电气距离要求,同时减小绝缘子迎风面积及重量,降低风压对绝缘子变形的影响,考虑采用变径结构设计,采用2 段不同芯棒直径组成,以获得良好的刚性并保证绝缘子具有一定韧性,总体结构如图1 所示。

图1 变径防风偏绝缘子结构
2 变径绝缘子挠度计算
防风偏复合绝缘子的端部挠度在工程应用中至关重要,挠度过大可能导致风偏间隙不足。该结构在风荷载、自重及跳线荷载作用下,可简化成端部受集中荷载的悬臂梁结构,芯棒受弯时符合平截面假定,在受横向力P 作用后,横截面仍为平面,且垂直于挠曲线。变径结构芯棒的计算模型如图2(a)所示,简化为变截面的悬臂梁,端部作用集中荷载P。采用叠加原理,首先将该变截面悬臂梁挠度看作以下2 部分组成:AC 段的弯曲所引起的挠度和BC 段的弯曲所引起的挠度。可单独求解这些挠度,然后,再将它们叠加以求得总挠度。
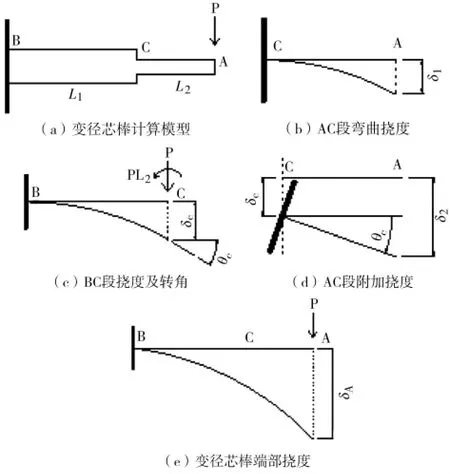
图2 变径防风偏绝缘子端部挠度计算过程
该梁AC 段的弯曲所引起的挠度:假设该梁在点C 处保持刚性,以致于该梁在该点处既不发生挠曲,也不发生转动[图2(b)]。由于AC 段的长度为L2、惯性矩为I2,因此,点A 挠度δ1可按照式(1)计算。
该梁BC 段的弯曲所引起的挠度:该梁BC 段的行为类似于一根悬臂梁[图2(c)],而且在点A 处产生了挠度。该悬臂梁的自由段承受着一个集中荷载P 和一个力矩PL2。因此自由端的挠度δc和转角θc可分别按照式(2)及式(3)计算。
该挠度和转角对A 端处的挠度提供了1 个附加的挠度δ2[图2(d)]。再次把AC 段表示为1 根悬臂梁,但现在,其支座(点C 处)向下移动了1 个δc的距离,且逆时针旋转了1 个角度θc[图2(d)]。这些刚性位移在A 段处产生了1 个向下的位移δ2,按照式(4)计算。
原悬臂梁自由端处的总挠度δA[图2(e)]等于挠度δ1和δ2的总和,按照式(5)计算。
3 变径复合绝缘子仿真分析
为分析变径复合绝缘子结构的力学特性,下面采用ABAQUS 对其中芯棒部分进行有限元仿真,并结合等径芯棒结构进行对比分析。复合绝缘子芯棒采用环氧玻纤制作,为线弹性各向异性材料,根据生产厂家试验资料,纵向的弹性模量、泊松比、剪切模量为45 GPa、0.3、5.1 GPa,横向的弹性模量、泊松比、剪切模量分别为14 GPa、0.1、0.3 GPa,弯曲强度为900 MPa。绝缘子底座采用Q355B 钢材,变径处的连接金具采用#45 钢,均为线弹性各向同性材料,屈服强度分别为275 MPa、530 MPa。
考虑福建沿海台风区典型条件,设计基本风速为37 m/s,500 kV 跳线采用4×630 截面导线,考虑跳线风荷载的高空系数、铁塔转角度数及跳线串引流线的张力合力,作用于防风偏绝缘子高压端的水平合力最大值近4 kN。因此在绝缘子的端部沿Y 轴负方向施加4 kN 的集中荷载,并将底座完全固结。
根据最大畸变能密度理论,无论什么应力状态,只要畸变能密度υd 达到与材料特性有关的某一极限值,材料就发生屈服,因此定义芯棒的承载力极限状态为Mises 应力达到弯曲极限强度900 MPa。根据电气间隙要求,端部变形达到1.6 m 时也可认为芯棒达到正常使用极限状态。
采用上述方法对变径芯棒进行仿真分析,典型芯棒尺寸选取第一段大直径D1=90 mm、第二段小直径D2=45 mm、第一段长度L1=2 965 mm、第二段长度L2=1 900 mm。根据仿真结果,竖向位移(U2)云图及局部Mises 应力云图如图3~5 所示。
从图3 可以看出变径结构第一段芯棒变形较小,第二段芯棒弯曲变形曲率明显大于第一段,变形主要集中在第二段,突变发生在中间金具连接处。该位置为芯棒薄弱点,如图5 所示,局部Mises 应力最大值发生在该位置的下平面。将竖向位移沿长度方向绘制成芯棒变形曲线,如图4 所示,端部最大仿真位移为1 567 mm。根据该尺寸的芯棒试验数据为1 453 mm,误差仅7.8%。试验变形曲线如图6 所示,与仿真结果相似,薄弱点发生在变截面处。综上可知,有限元模型是可靠有效的。
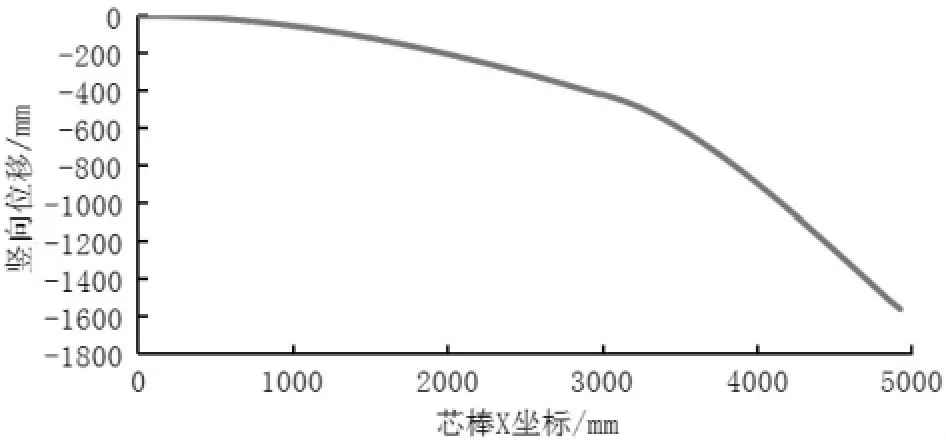
图4 变径芯棒90~45 竖向位移曲线

图5 变截面处Mises 应力云图

图6 变径芯棒弯曲试验
为对比分析变径结构特性,选取典型等径芯棒(直径D=80 mm)做仿真分析,竖向位移(U2)如图7~8 所示,变形均匀无突变,最大变形发生在端部荷载加载点,最大Mises 应力出现在与底座连接处下平面,为薄弱点,该位置的局部Mises 应力云图如图9 所示,与变径芯棒薄弱处位于变截面处不同。

图7 等径芯棒竖向位移U2 云图
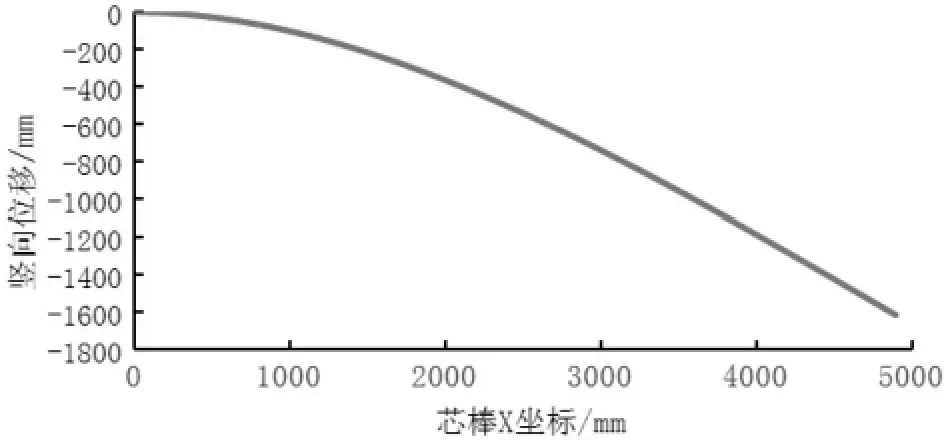
图8 等径芯棒80 竖向位移曲线
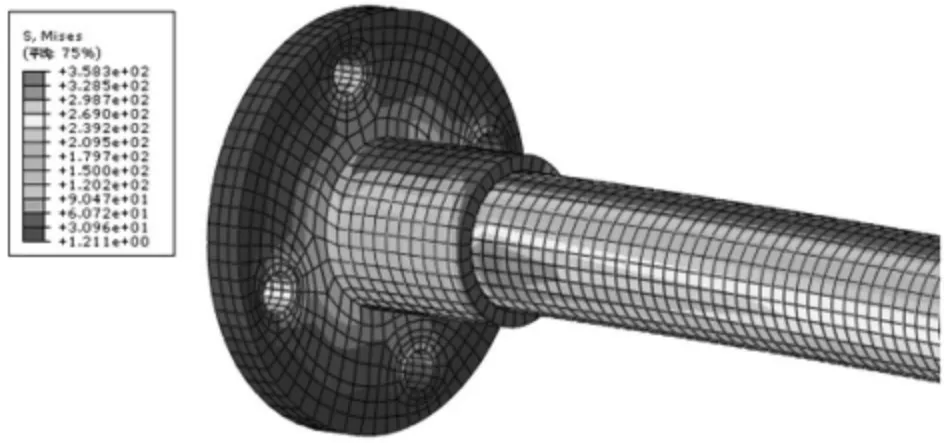
图9 等径芯棒端部Mises 应力云图
4 变径复合绝缘子参数化分析
变径防风偏绝缘子芯棒的结构主要参数有长度、直径、变径位置,其余材性参数及边界条件与上文相同。参考500 kV输电线路绝缘子联长,参数化分析时芯棒总长取L=4.9 m。当芯棒为等径实心棒时,芯棒端部受集中荷载下的挠度为:Y=PL3/3EI,由此可推算出直径D,按照式(6)计算。
根据环氧玻纤复合芯棒的材性试验取弹性模量E=45 GPa,电气间隙要求端部的位移不宜超过1.6 m,因此偏移量Y 暂定1.6 m,当L=4 900 mm,计算得出等径芯棒直径D=81.6 mm。下文将围绕该理论推算直径,结合绝缘子生产工艺模数,分析多种参数组合的等径结构、变径结构端部位移及应力响应。
由于两段芯棒的中间存在转接金具,厚度10 mm,底座厚度25 mm,因此芯棒的实际总长L=L1+L2=4 865 mm。
为对比分析变径芯棒的力学特性,同时选取了4 组等径芯棒作为参照,第1~4 组为等径芯棒,第5~13 组为变径芯棒。δ 为本文式(5)的理论挠度,U2为芯棒端部仿真竖向位移,η 为端部挠度与变截面处挠度之差占端部挠度的比例,反映第二段(小直径)对总挠度的贡献,P 为芯棒最大Mises 应力,结果如表1 所示。
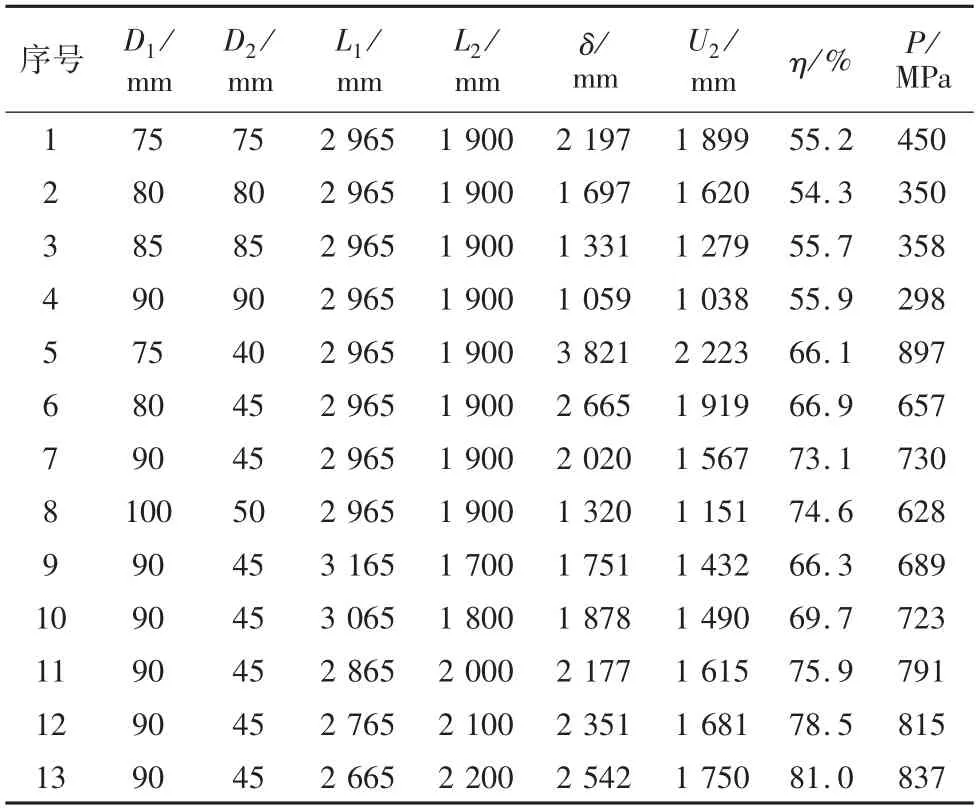
表1 芯棒尺寸参数化分析
对比第2 组与第7 组挠度数据,第7 组变径芯棒端部仿真挠度U2是第2 组等径芯棒的97%,但是体积只占89.5%,意味着变径芯棒可以用更少的材料达到更优的效果,通过调整尺寸参数,可以具备更优良的刚度。第7 组最大Mises 应力达730 MPa,而第2 组为350 MPa,均未超过环氧玻璃纤维的抗弯强度,因此变径结构能更好地利用复合材料的纵向力学性能。
通过对比第5~8 组数据,第7 组数据的端部挠度为1 567 mm,最接近前述定义的正常使用极限状态—端部挠度达1.6 m,且最大Mises 应力未达到弯曲极限强度,因此推荐采用该组尺寸作为福建沿海台风区(基本风速37 m/s)500 kV 线路的防风偏复合绝缘子参数。
对比理论计算挠度δ 与仿真挠度U2,等径芯棒的两者差值较小,仿真挠度占理论挠度的86%~98%,说明仿真结果的有效性。但是变径芯棒的两者差值扩大,仿真挠度占理论挠度的58%~87%,这是由于理论计算公式的前提是假定芯棒为各向同性的线弹性材质,且受弯时符合平截面假定,同时不考虑变截面处采用高强度钢材进行压接处理的影响,而有限元模型中芯棒为正交各向异性材料,且中间接头变径处刚度更大,对端部挠度存在减小作用。
为研究变径位置对芯棒力学性能的影响,分析第9~13 组不同的变径位置参数,结果表明,随着第2 段长度L2的增加,芯棒挠度与最大Mises 应力均逐渐增加,成正相关的变化趋势。L2每增加100 mm,芯棒端部挠度平均增加64 mm,最大Mises 应力平均增加30 MPa。
分析第7、9~13 组变径芯棒第二段对总挠度的贡献比例η,可知变径芯棒的端部挠度主要来自第二段,占比达66.3%~81.0%,且随着第2 段(小直径段)长度L2的增加,该占比亦逐渐增大,因此第二段芯棒的直径和长度对整体性能起决定性作用。L2每增加100mm,第二段挠度对端部挠度的贡献比例增加约2.9%。
5 结论
本文给出了变径防风偏绝缘子结构的端部挠度理论计算公式,并与仿真结果吻合良好。
等径芯棒弯曲变形均匀,薄弱点在支座处;变径芯棒的挠度主要发生在小直径段,占比达66.3%~81.0%,中间连接处为薄弱点。
通过一定的参数设计,在满足电气间隙及承载力的要求下,变径芯棒相比等径芯棒能更节省材料,更好地利用复合材料的纵向力学性能。推荐D1=90 mm、D2=45 mm 的参数组合作为福建沿海台风区(基本风速37 m/s)500 kV 线路的防风偏复合绝缘子参数。
变径芯棒的第二段直径和长度对整体性能取决定性作用,L2每增加100 mm,芯棒端部挠度平均增加64 mm,最大Mises 应力平均增加30 MPa,第2 段挠度对端部挠度的贡献比例增加约2.9%。

