极轴式定焦点菲涅尔聚光器的聚光理论与实验研究
王海 伍俊研 谢沛烁
(肇庆学院机械与汽车工程学院 广东肇庆 526061)
0 引言
在菲涅尔透镜的设计中,通常采取一般设计方法,即选取太阳光谱中某一代表波段在PMMA 材料中的折射率作为设计基准,继而对透镜的相关参数进行设置。因在地面上观测的太阳辐射的波段范围大约为0.295~2.5 μm,其在PMMA 材料中的折射率均不相同,导致不同波长的光在菲涅尔透镜中所形成的焦距不同,即形成色散。LORENZO 等[1]提出色散的存在会降低菲涅尔透镜的聚光效率,尤其对聚光比大、焦径比小的菲涅尔透镜的影响更大;JING 等[2]则结合上述太阳光谱特性和多焦点设计方法,设计了1 种应用于光伏系统的高聚光比菲涅尔透镜。上述研究均表明,菲涅尔透镜在太阳能领域的应用中需考虑色散带来的影响,尤其是聚光比高、焦径比小的菲涅尔透镜。另外,由于菲涅尔透镜在设计过程中的入射光线为平行光,而太阳光并非绝对的平行光,具有16′的半平均视角,该视角的存在对焦平面处形成的焦斑具有增大趋势[3]。而常见的太阳能集热器的开口直径一般在120 mm 左右。若聚光器跟踪精度不够,太阳光倾斜入射,则可能会导致焦斑脱离太阳能集热器开口范围。
本文提出1 种确定菲涅尔透镜最小焦斑半径的方法,并将菲涅尔透镜到该焦平面的距离作为菲涅尔透镜理论焦距。在笔者前期提出的极轴式定焦点菲涅尔聚光器的工作基础上[4],进一步研究聚光器全年的聚光焦斑偏移情况,验证该聚光器可实现全年定焦点聚光,为后期极轴式定焦点菲涅尔聚光器的应用提供依据。
1 菲涅尔透镜理论焦距及焦斑半径
本文所用菲涅尔透镜为单焦点菲涅尔透镜,如图1(a)所示。图1(b)为菲涅尔透镜理论聚光原理图。实际太阳光垂直照射聚光过程中,由于太阳光具有16′的半平均视角以及色散作用的存在,导致在菲涅尔透镜焦平面处形成的是具有一定大小的圆形焦斑,而非理想情况中的点。同时,由图1(b)可知,在设计焦距f 下形成的焦斑半径不一定为最小值。为了能够在实际应用中提高菲涅尔透镜的聚光比,则需要计算出该菲涅尔透镜的最小焦斑半径和对应的位置,并分别作为理论焦斑半径和理论焦距。
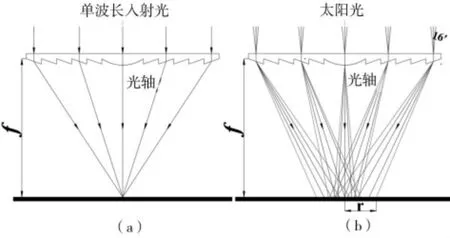
图1 菲涅尔透镜光学原理图
图2 为菲涅尔透镜理论焦距计算原理图。一般可认为菲涅尔透镜最外环形成的焦斑大小可以类比为透镜形成的焦斑大小。为从理论上验证聚光器可实现全年定焦点聚光,则要求理论推导出的最外环焦斑在全年的偏移情况均在允许范围以内,即焦斑中心不脱离集热器开口范围。同时采用CCD 对实际聚光焦斑进行拍摄,与理论推导结果进行对比分析,验证聚光器可实现定焦点聚光。实验所拍摄的焦斑为可见光形成的焦斑[5]。因此,在理论推导菲涅尔透镜焦斑时,选取太阳辐射的波段范围0.4~0.76 μm 的可见光作为研究对象。
图2 中T、C、B 等3 条线分别代表太阳光中的顶部光线、中心光线、底部光线。由于不同波长的光在PMMA 材料中的折射率不同,故聚光后所形成的焦点位置也不相同。德国肖特(Schott)玻璃公司给出了PMMA 材料的色散公式如式(1):
式中:a0=2.18 645820;a1=-2.44753480×10-4;a2=1.41557870×10-2;a3=-4.43297810×10-4;a4=7.76642590×10-5;a5=-2.99363820×10-6。
由色散公式计算得到的折射率可知,入射光的波长越大,其在PMMA 材料中的折射率越小。为了准确计算菲涅尔透镜的理论焦距位置以及焦斑半径,本文选取0.4 μm 和0.76 μm波长的光作为计算基准,在PMMA 材料中对应折射率分别为1.507 3、1.486 6。结合菲涅尔透镜聚光过程中的极限位置,即考虑T 光线中的0.76 μm 的光波和B 光线中的0.4 μm 的光波经菲涅尔透镜聚光后所形成的叠加区域最小位置和对应的半径分别作为理论焦距和焦斑半径。
由图2 可知,对于T 光线中的波长0.76 μm 的光,根据光的折射定律式(2)和式(3):
式中:ε 为太阳光半平均视角;N 为空气折射率,近似等于1;Nn为波长0.76 μm 的光在PMMA 中折射率;βn为其第一折射角;κn为其第二折射角;αm为菲涅尔透镜最外环(第m 齿)的倾斜角,其中透镜半径为R,环距为b,镜面厚度为t。
由几何关系可得式(4):
同理可知,对于对于B 光线中的波长0.4 μm 的光,根据光的折射定律式(5)和式(6)。
式中:N1为波长0.4 μm 的光在PMMA 中折射率;β1为其第一折射角;κ1为其第二折射角。由几何关系可得式(7):
由上述0.4 μm 和0.76 μm 的波长光所得对应的焦距f1、fn以及相关几何关系,则可得式(8)和式(9):
式中:f0为理论推导所得焦距,r0为理论推导所得焦斑半径。
图3 展示了极轴式定焦点菲涅尔聚光器的工作原理。在聚光器进行固定焦点聚光跟踪时,它首先会根据太阳赤纬角的大小,绕赤纬轴进行俯仰运动定轨,然后沿极轴自东向西跟踪太阳,跟踪角速度与地球自转角速度相同。因此,菲涅尔透镜与极轴呈现出空间对称性。菲涅尔透镜会根据太阳赤纬角的变化,沿着以赤纬轴为转动中心、透镜焦距F 为半径的圆弧轨迹上移动。当太阳的光垂直照射在菲涅尔透镜上时,其聚光焦斑正好落在极轴与赤纬轴的交汇位置。
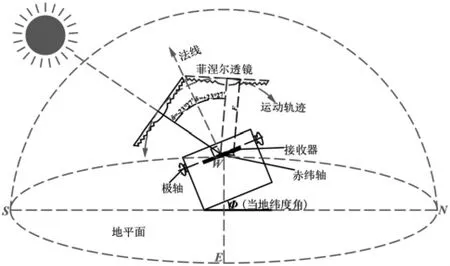
图3 极轴式定焦点菲涅尔聚光器工作原理图
2 聚光焦斑偏移情况分析
2.1 理想跟踪条件下聚光焦斑偏移
在理想跟踪条件下,聚光器与入射太阳光不存在跟踪角度误差,但聚光器在跟踪太阳位置的过程中,接收器平面与聚光器除特殊位置保持平行状态外,其余位置均存在夹角θ',即菲涅尔透镜光轴与接收器平面法线存在夹角θ'。由图4、图5所示,聚光焦斑形状位置会随着夹角的变化而改变。
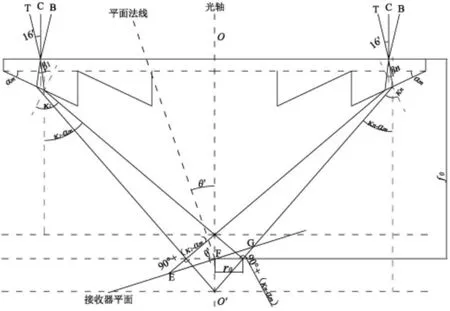
图4 赤纬角0°≤δ≤+23°27′时理想跟踪条件下聚光焦斑形状位置变化图

图5 赤纬角-23°27′≤δ≤0°时理想跟踪条件下聚光焦斑形状位置变化图
对固定安装的接收器平面,菲涅尔透镜的光轴与接收器平面法线的夹角θ' 可用如下公式(10)计算:
式中:φ 为地理纬度;φ 为接收器倾角(接收器平面与地平面夹角);γ 为接收器方位角;ω 为太阳时角;δ 为太阳赤纬角。
由于在该聚光器中,接收器平面倾角与当地纬度相同,且朝向正南,即φ=φ,γ=0°,上式可简化为式(11):
当赤纬角0≤δ≤+23°27′时,聚光焦斑偏移情况如图4 所示。由图4 中几何关系可得式(12)和式(13):
同理可知,当赤纬角-23°27′≤δ≤0°时,聚光焦斑偏移情况如图5 所示。由图5 中几何关系可得式(14)和式(15):
由图4、图5 可知,聚光焦斑长度为EG。
为了更准确地描述聚光器的焦斑位置偏移情况,本文将焦斑几何中心的位置作为聚光焦斑位移中心。当聚光焦斑位移中心偏离半径为60 mm 的圆环边界时,表明聚光器无法实现定焦点聚光。通过对理论聚光焦斑的几何关系进行计算,可以得到聚光焦斑位移中心与接收器平面几何中心的位置偏差值,即焦斑中心偏差值。最后,计算该位置偏差值与圆环半径(60 mm)的百分比值,可以得到相对位置偏差情况。
2.2 实际跟踪条件下聚光焦斑偏移
为了研究极轴式定焦点菲涅尔聚光器的实际跟踪条件下的聚光焦斑偏移情况,把广州地区(北纬23°08′)作为研究对象,搭建定焦点聚光性能测试系统,测量装置主要包括极轴式定焦点聚光器、直射辐照计、朗伯靶、CCD 照相机、中性密度滤光片(ND-filter)和数据采集系统,如图6 所示。
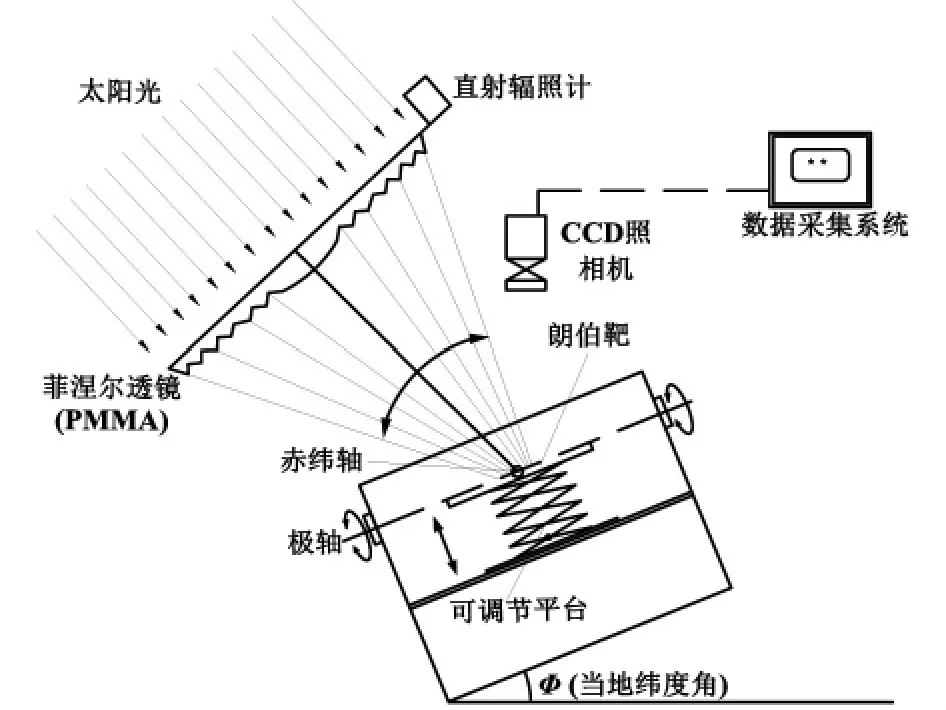
图6 定焦点聚光性能测试系统
该聚光器中采用的菲涅尔透镜中PMMA 材料折射率n=1.49,半径R 为550 mm,环距b 为1 mm,焦距f 为1 000 mm。其中菲涅尔透镜最后外环的倾斜角tanαm=0.797。由式(2)~(9)可得,该菲涅尔透镜的实际焦距f0=936.2 mm,焦斑半径r0=936.2 mm;聚光器的极轴跟踪装置为光电式单轴太阳能跟踪器;聚光器赤纬角跟踪以手动调节的方式实现。太阳直射辐射采用FZ-A 型直射辐照计测量,其准确度为±5%。朗伯靶是规格为240 mm×240 mm 的矩形铁靶,该朗伯靶通过安装在可调节平台上将其调至聚光器焦点处,此外对靶表面喷涂漫反射率达到90%以上的Al2O3,使其接近于朗伯反射面。实验采用卡西欧数码相机作为探测器采集聚光焦斑的图像信息,前方放置中性密度滤光片。最后通过数据采集系统对图像进行二值化、去除噪声等操作,采用椭圆拟合的方式求取图像中的焦斑长度以及焦斑中心偏差值。
由图3 可知该聚光器为南北放置,东西跟踪的方式,并根据实验当天太阳赤纬角(-23°07′)调整聚光器赤纬轴转动角度。选取真太阳时10∶00、12∶00、14∶00 时刻进行定焦点聚光性能测试实验,实验过程中太阳直射辐射值基本维持在(540±5)W/m2范围,利用CCD 相机对朗伯靶上的聚光焦斑进行拍摄。实验处理后的聚光焦斑椭圆拟合图如图7 所示,其中X 轴表示南北方向,朝南为正;Y 轴表示东西方向,朝东为正。
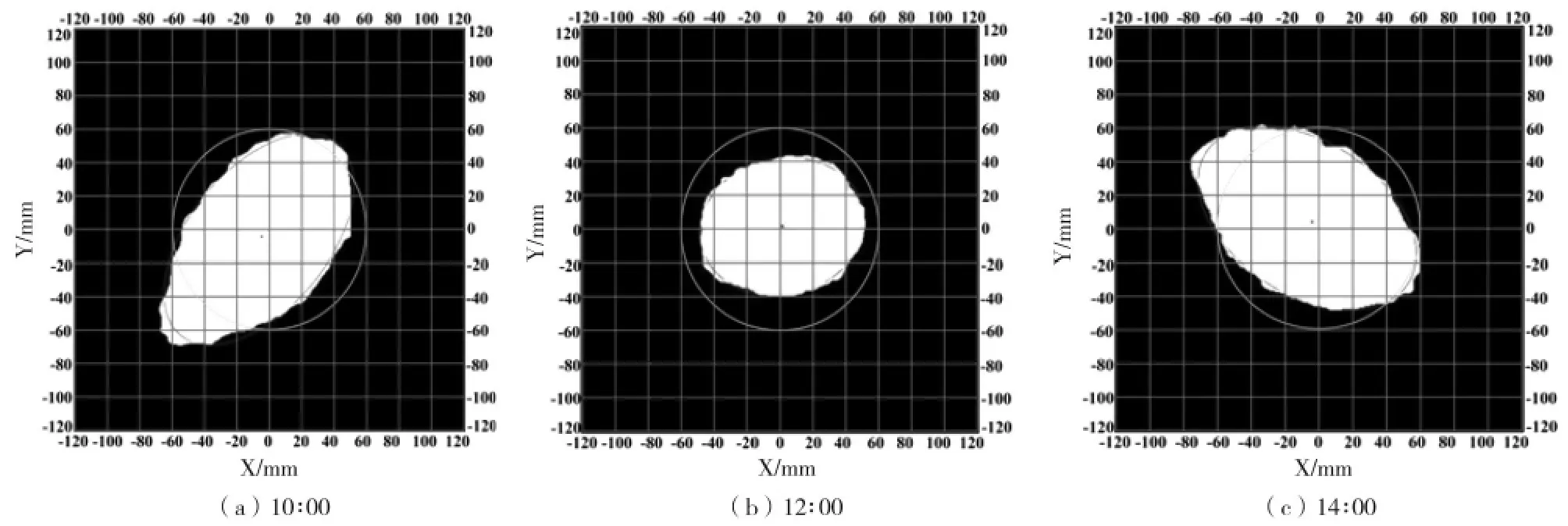
图7 不同真太阳时下聚光焦斑分布情况
同时根据实验相关参数,利用式(14)、(15)等计算理想跟踪条件下聚光焦斑偏移情况,可得理想和实际跟踪条件下聚光焦斑偏移情况如表1 所示。对实验所得的焦斑图进行测量,可得到聚光焦斑中心与朗伯靶几何中心的位置偏差值,并计算该位置偏差值与圆环半径(60 mm)的百分比值,即可得到焦斑相对位置偏差情况。理论分析结果中焦斑相对位置偏差最大值为7.0%,对应的焦斑长度为161.0 mm;实验结果中焦斑相对位置偏差最大值为11.2%,对应的焦斑长度为151.5 mm,且焦斑均基本分布在半径为60 mm 圆环区域内。表明理论分析与实验结果都能实现定焦点聚光,且聚光焦斑长度基本一致,即理论分析模型可靠,可利用上述理论模型验证该聚光器定焦点聚光的可靠性。
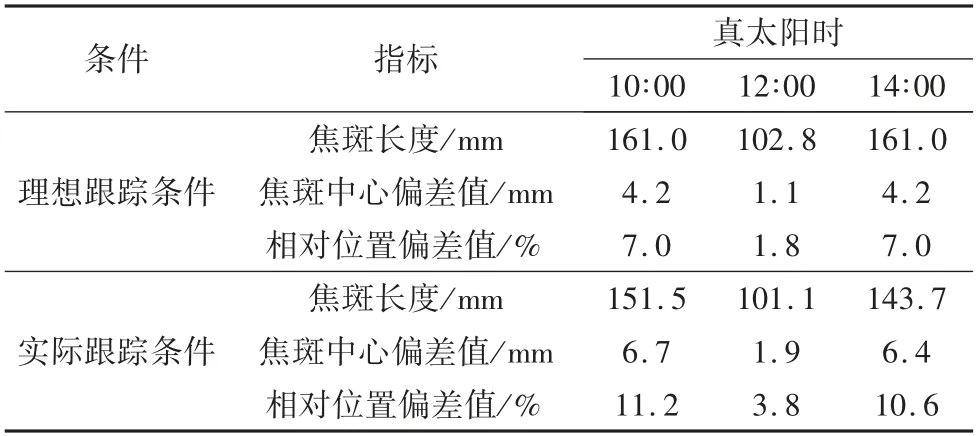
表1 理想与实际跟踪条件下聚光焦斑偏差情况
2.3 聚光器全年聚光焦斑偏移
为了更全面地验证聚光器的定焦点聚光的可靠性,并确定接收器平面上的焦斑位置偏差范围,本文选取聚光器在全年运行过程中的极端位置进行理论模型分析。继续以广州地区作为研究对象,选取太阳赤纬角分别-23°27′、0°、+23°27′时,对应真太阳时为10∶00~14∶00 范围内,时间间隔为2 h 的聚光焦斑变化情况进行模拟研究。如表2 所示为极轴式定焦点聚光器全年聚光焦斑偏差情况,由表2 中可知,聚光器全年运行过程中,焦斑长度最大值为162.2 mm,对应的焦斑中心偏移量为4.3 mm,相应的太阳位置为太阳赤纬角-23°27′和+23°27′,真太阳时为10∶00 和14∶00 时刻。尽管焦斑长度最大值为162.2 mm,但对应的焦斑中心偏差值仅为4.3 mm,相对位置偏差值为7.2%,焦斑中心依然包含于半径为60 mm 的圆形区域内,即极轴式定焦点聚光器能够实现全年固定焦点聚光。
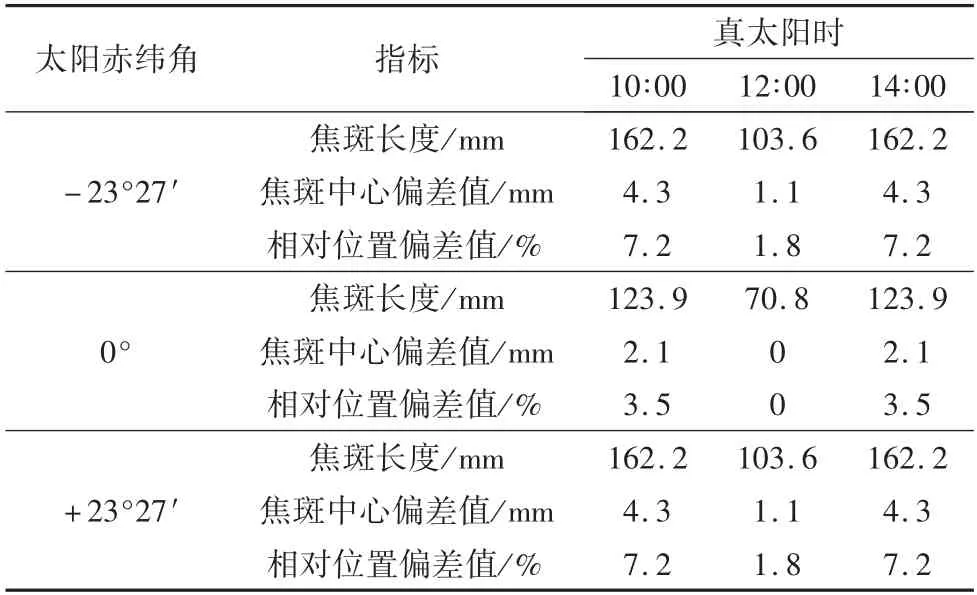
表2 全年聚光焦斑理论位置偏差情况
3 结论
本文针对聚光比高、焦径比小的菲涅尔透镜,理论推导了菲涅尔透镜的理论焦距及焦斑半径。并在此基础上对菲涅尔极轴式固定焦点聚光器,作了定焦点聚光的原理分析。为验证该聚光器的定焦点聚光的可靠性,采用理论模型分析和定焦点聚光性能实验结合,得到结论如下:
(1)由于实际太阳光具有16′的半平均视角以及色散作用的存在,提出聚光比高、焦径比小菲涅尔透镜理论焦距及焦斑半径确定的计算公式。
(2)通过理论模型分析与定焦点聚光性能实验的对比研究可知,理论分析结果中焦斑相对位置偏差最大值为7.0%,对应的焦斑长度为161.0 mm;实验结果中焦斑相对位置偏差最大值为11.2%,对应的焦斑长度为151.5 mm,且焦斑均基本分布在半径为60 mm 圆环区域内。表明理论分析与实验结果都能实现定焦点聚光,且聚光焦斑长度基本一致,即理论分析模型准确可靠。
(3)进一步对全年聚光器全年聚光焦斑偏移情况分析可得,焦斑长度最大值为162.2 mm,对应的焦斑中心偏差值仅为4.3 mm,相对位置偏差值为7.2%,焦斑中心依然包含于半径为60 mm 的圆形区域内,即极轴式定焦点聚光器能够实现全年固定焦点聚光。

