短轨枕区段钢轨吸振器对钢轨波磨抑制机理的研究

崔晓璐,徐晓天,文孝霞,吕 东,汤金伟

(1. 重庆交通大学 机电与车辆工程学院,重庆 400074; 2. 广东铁路有限公司惠州工务段,广东 惠州 516023)

0 引 言

随着各大城市地铁网络的飞速扩张,钢轨波磨问题也日益突出[1]。虽然在附加钢轨吸振器后,钢轨波磨问题得到了一定程度的改善[2],但钢轨波磨的影响因素十分复杂[3],钢轨吸振器对钢轨波磨抑制机理还需展开进一步研究。

目前,针对钢轨吸振器对钢轨波磨的抑制机理和方法,国内外学者开展了一系列研究。H.P.LIU等[4]通过建立梁-弹簧-阻尼模型,并模拟了钢轨吸振器各参数对轮对-钢轨-吸振器系统振动声辐射和振动响应的影响,结果表明:钢轨吸振器主要是做刚体运动,其次是弯曲变形;孙晓静等[5]建立了轮对-钢轨-吸振器系统的理论模型,并深入探讨了质量、阻尼和刚度等各参数对钢轨吸振器吸振特性影响,得出了相匹配参数组合将会出现较好吸振效果的结论;文永蓬等[6]基于钢轨Pinned-Pinned振动可能会引起钢轨波磨理论,分析了钢轨在安装钢轨吸振器后能抑制Pinned-Pinned振动的事实,从而能有效控制钢轨波磨在指定频率区段中钢轨波磨发展;刘上[7]建立了轮对-钢轨-吸振器系统的三维动力学模型,分析了钢轨吸振器在不同参数下对指定频率区段内减振降噪效果,并进行了实验验证和参数优化;J.R.CETTOUR等[8]结合有限元模型和边界元法,将钢轨吸振器附着于钢轨的轨腰处,分析了钢轨吸振器的减振效果。

综上,前期的研究主要是从动力学角度来分析钢轨吸振器对钢轨波磨的抑制作用,未能结合钢轨波磨产生的机理来进行分析。因此,笔者从轮轨系统摩擦自激振动诱导钢轨波磨的观点出发,以重庆1号线双碑—石井坡区间的小半径曲线段钢轨作为研究对象,建立了车辆-轨道系统动力学模型,并分析了其动力学特性;建立了相应区段轮对-钢轨-吸振器系统的有限元模型,采用复特征值法和瞬时动态法分析了钢轨吸振器对轮轨系统摩擦自激振动的抑制机理,并进一步对比了轨腰吸振器和轨底吸振器抑制钢轨波磨的效果;最后分析了这两种吸振器参数对钢轨波磨的影响规律。

1 钢轨吸振器现场测试

笔者对重庆地铁1号线双碑—石井坡区间的钢轨进行了长期的现场调研,发现小半径曲线轨道上的钢轨波磨问题较为严重。为此,重庆轨道交通集团对该区间的钢轨进行了打磨处理并附加了钢轨吸振器,之后的7个月内钢轨表面波磨有了很大程度改善,如图1。据钢轨表面粗糙度实测数据,在安装吸振器后的钢轨几乎无波磨现象,而未安装钢轨吸振器的钢轨则出现了明显波磨,且钢轨表面粗糙度级最大值为17.8 dB,存在严重超限情况,如图2。

图1 钢轨波磨现象Fig. 1 Rail corrugation phenomenon

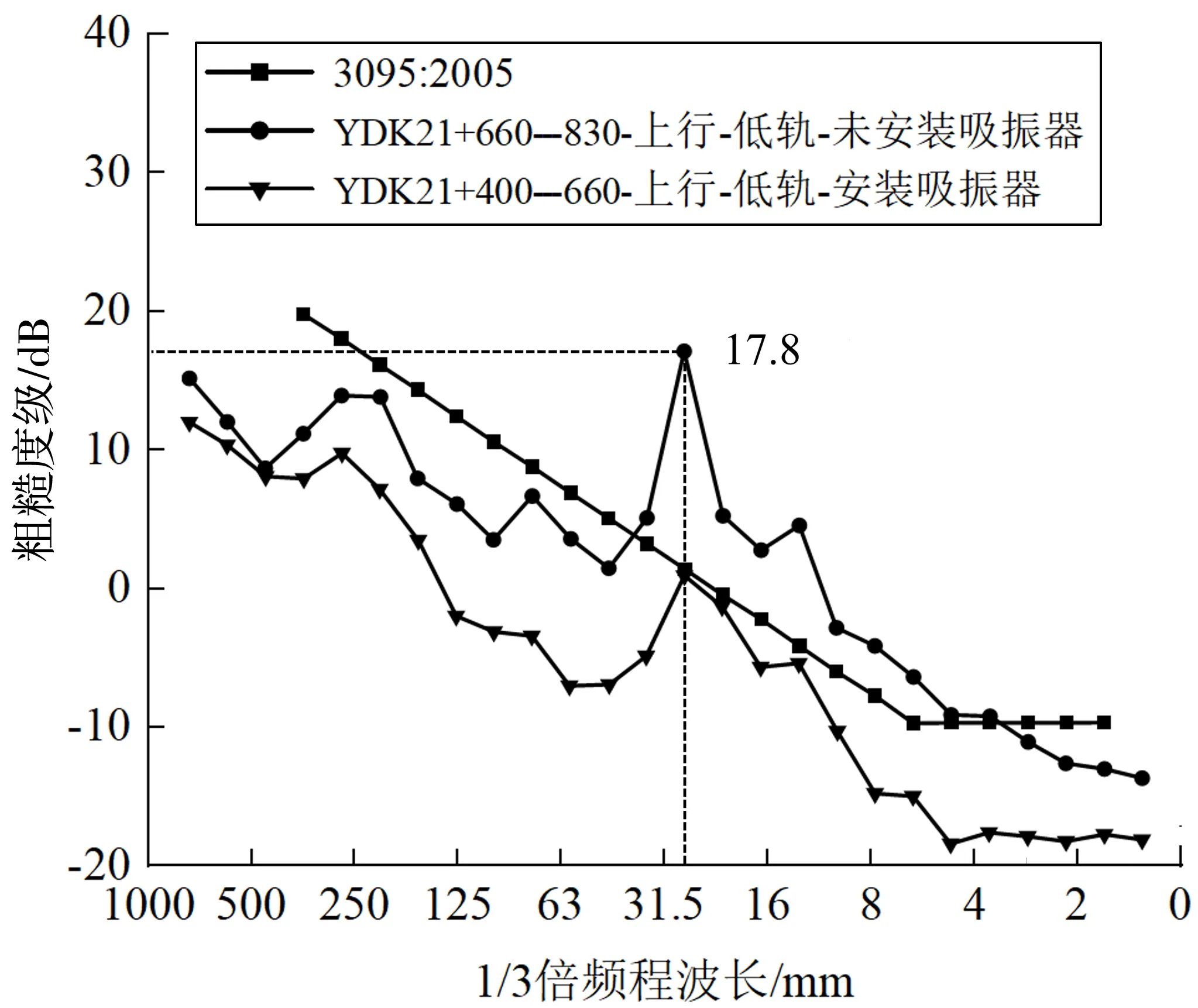
图2 钢轨表面粗糙度级对比Fig. 2 Comparison diagram of rail surface roughness level

该区段钢轨为短轨枕支撑结构,圆曲线半径为300 m,轨距为1 440 mm,钢轨型号为60 kg/m,轨底坡为1/40,扣件为DTVI2型,扣件间距为625 mm,列车通过该区段速度约为60～80 km/h。经测量发现,该路段钢轨上出现了波长约为30～50 mm的波磨,由此可计算出诱发钢轨波磨的振动频率(λ=v/f)约为330～740 Hz。结合长期调研结果发现:在安装吸振器后,钢轨波磨得到很大程度缓解;轨腰处的附加钢轨吸振器对钢轨波磨的产生与发展具有一定抑制作用。

2 钢轨波磨数值仿真

2.1 车辆-轨道系统的动力学模型

为研究短轨枕支撑小半径曲线区段的轮轨间蠕滑特性,根据重庆地铁1号线双碑—石井坡区间的相关参数建立了车辆-轨道系统动力学模型[9],车辆为B型地铁,如图3。车辆主要包括了车体、转向架、导向-从动组合轮对,两两之间均采用弹簧阻尼单元方式连接,以此方式模拟了一系、二系悬挂装置上3个方向的刚度和阻尼。整条轨道线路的设置共分为5段(直线段L1、L5,长度为100 m;缓和曲线段L2、L4,长度为65 m;圆曲线段L3,长度为265 m,曲线小半径为300 m,线路超高均为0.11 m)。车辆参数和轨道线路参数设置与实际一致。

图3 车辆-轨道系统的动力学模型Fig. 3 Dynamic model of vehicle-rail system

2.2 轮对-钢轨-吸振器有限元模型

笔者考虑了轨腰式和轨底式两种吸振器。结合现场测试和车辆-轨道系统动力学结果,分析了轮对与钢轨之间的接触情况和受力形式,轮轨系统接触模型如图4(a)。图4(a)中:导向轮对左右两边与钢轨的接触角分别为δL、δR;轮对两头轴箱处分别受到来自垂直方向的悬挂力FSVR、FSVL和水平方向的悬挂力FSLR、FSLL的作用;垂直于轮轨接触面的法向接触力分别为NR、NL;轮轨间的蠕滑力分别为FR、FL;DTVI2扣件中横、垂两个方向刚度分别为KRL、KRV;横、垂两向的阻尼分别为CRL、CRV。轨腰吸振器与轨底吸振器安装示意如图4(b)。图4(b)中:轨腰吸振器质量块安装在钢轨轨腰两侧,轨底吸振器质量块安装在钢轨底部,这两者间为弹性材料层;在建模中,质量块采用弹性体进行模拟,弹性材料层采用弹簧-阻尼系统进行模拟,故钢轨吸振器能简化成质量-弹簧-阻尼系统。

结合轮轨模型,建立了轮对-钢轨-吸振器系统的有限元模型,如图5。为降低钢轨末端所产生的端面效应对有限元分析结果产生影响[10],短轨枕的数量设为60;钢轨底部与短轨枕接触部分采取点对点弹簧-阻尼单元连接,用以替代扣件在系统中的减振作用;短轨枕底部采用接地弹簧单元支撑,用来模拟地基支撑作用。轨腰吸振器如图5(a),轨腰吸振器质量块是由合金钢外壳和内部吸振材料组成,左右对称的两块吸振器质量约为11 kg[11]。轨底吸振器如图5(b),轨底吸振器设置在两扣件间钢轨的底部,单个吸振器质量与两个轨腰吸振器质量之和相同,质量比(吸振器质量与一跨长钢轨的质量之比)约为0.3。为保证两者可比性,需要将轨底吸振器的质量、刚度和阻尼等影响系数设置为轨腰吸振器的2倍[12]。根据重庆地铁1号线现场测试数据和相关数据,笔者所选取的有限元模型中各部分材料参数如表1[9],连接参数如表2。

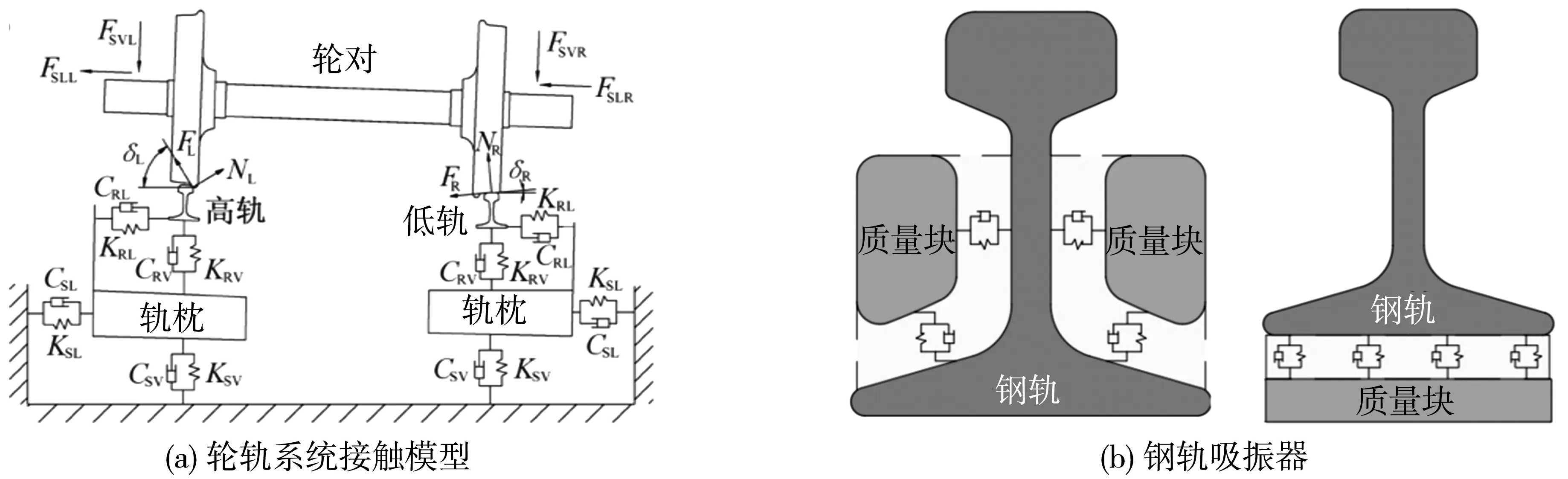
图4 短轨枕区段的轮轨模型Fig. 4 Model of the wheel-rail system in the short sleeper section

图5 轮对-钢轨-吸振器系统有限元模型Fig. 5 Finite element model of wheelset-rail-absorber system

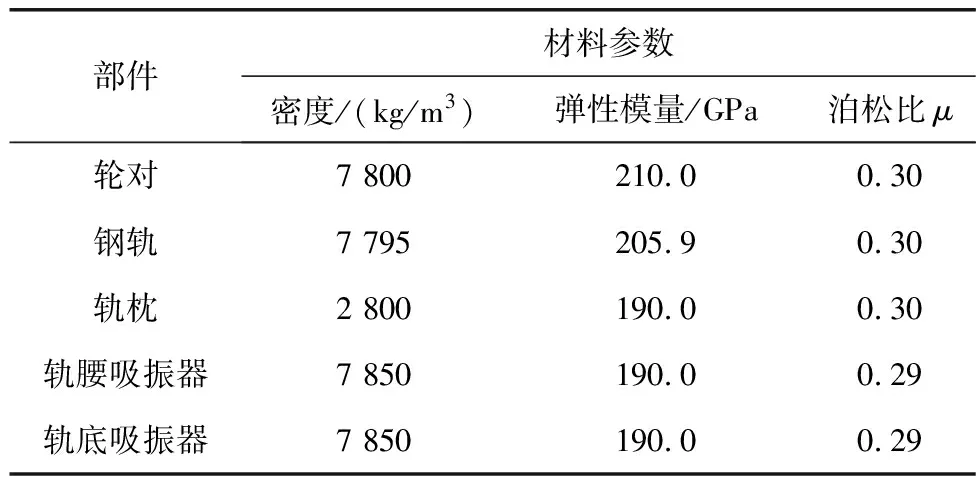
表1 有限元模型材料参数Table 1 Material parameters of finite element model

表2 有限元模型的连接参数Table 2 Connection parameters of finite element model

2.3 摩擦自激振动分析

在前期研究中,学界普遍认为波动的摩擦功会导致钢轨波磨。C.A.BROCKLEY等[13]提出了修正的磨损方程,如式(1):

W=K(H-C)

(1)

式中:W为单位时间磨损量;K为磨损常数;H为摩擦功率;C为耐久性摩擦功率。

W可解释因轮轨系统的摩擦自激振动而形成的钢轨波磨。在复特征值分析中,考虑轮轨间存在摩擦滑动作用,故系统运动方程[14]如式(2):

(2)

式中:Mf为系统质量矩阵;Cf为系统阻尼矩阵;Kf为系统刚度矩阵;x为节点位移向量。

当轮轨间的蠕滑力与滑动摩擦力接近时,意味着达到饱和状态[15],将导致轮轨系统失稳。依据特征方程,可得到通解如式(3)、式(4):

(3)

ξ=-α/(π|ω|)

(4)

式中:x(t)为轮对-钢轨-吸振器系统特征向量;t为时间;λf=αf+ jωf为复特征值,当复特征值实部出现正值后,则该系统将会出现一定程度的不稳定振动;αf为特征值的实部; j为特征值的虚部单位;ωf为轮轨系统固有频率;ξ为系统的等效阻尼比。

等效阻尼比也可用来判断系统摩擦自激振动发生的趋势。瞬时动态分析相对于复特征值而言,这两者差异来自于研究角度不同。前者是从时域角度得到系统的动态响应,后者则是从频域角度得到系统模态仿真结果。

在分析中,整个系统平衡方程是通过每个时间增量步的方式来建立(时刻t),如式(5)、式(6):

(5)

(6)

式中:Fp(t)为外部力向量;FI(t)为内部力向量;Δt为时间增量。

3 结果与分析

3.1 车辆-轨道动力学模型动力学分析

根据地铁车辆动力学特性,当地铁车辆运行到圆曲线区间时,低轨处的蠕滑合力非常靠近于摩擦力,而高轨处的蠕滑合力与摩擦力相差较远。因此可认为地铁在整个圆曲线区间行驶时,低轨处的轮轨间蠕滑力趋于饱和,如图6。

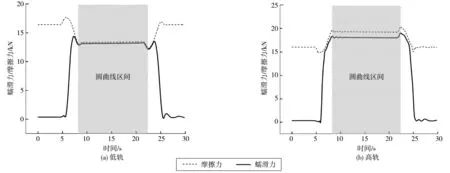
图6 轮轨间蠕滑力和摩擦力的变化关系Fig. 6 The relationship between the creeping force and friction between the wheels and rails

3.2 轮对-钢轨-吸振器系统的摩擦自激振动分析

基于轮轨摩擦自激振动理论,当车辆通过未设置钢轨吸振器的小半径曲线区段时,低轨处的车轮与钢轨之间蠕滑力趋于饱和,从而会诱导轮轨系统发生摩擦自激振动。因此笔者运用复特征值法和瞬时动态法别分析了轮对-钢轨-吸振器系统在频域和时域中的摩擦自激振动特性,对比分析了轮轨系统附加轨腰吸振器和轨底吸振器后对钢轨波磨的抑制效果。从频域上可得出轮轨系统摩擦自激振动频率和等效阻尼比的分布情况,如图7。

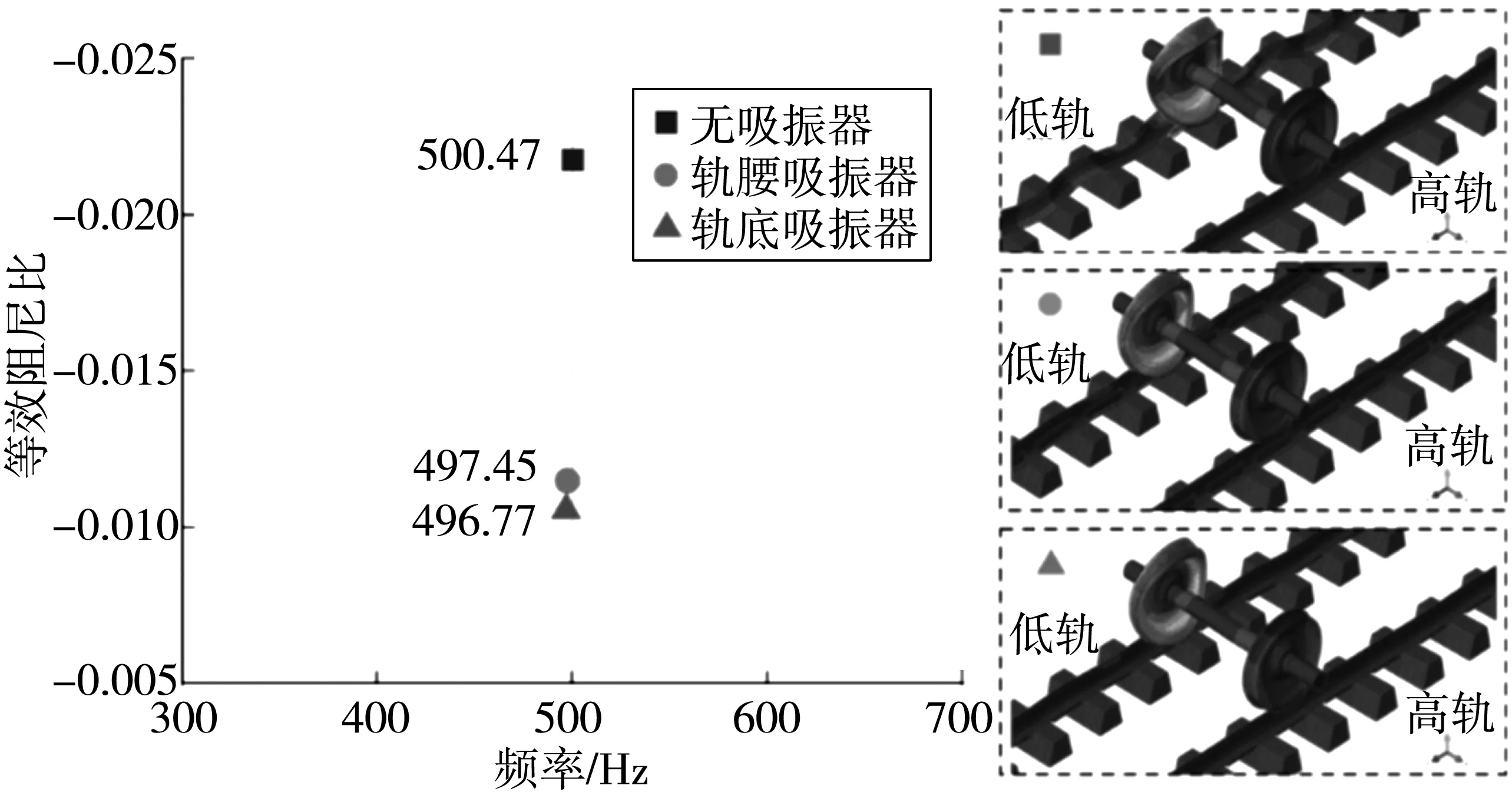
图7 等效阻尼比分布情况及模态Fig. 7 The distribution and mode of the equivalent damping ratio

未安装吸振器的轮轨系统中阻尼比最小值对应的振动频率为500.47 Hz,在此频率下轮轨系统最有可能发生摩擦自激振动。根据所对应的模态图可知:摩擦自激振动仅发生在低轨处,而高轨处未有变动。此外,分别对安装轨腰和轨底钢轨吸振器后的轮对-钢轨-吸振器系统复特征值分析结果显示:不稳定振动的主要频率相对于安装钢轨吸振器前几乎保持不变,但其对应的等效阻尼比明显增大,这说明轮对-钢轨-吸振器系统发生摩擦自激振动的可能性降低。该系统的摩擦自激振动频率与诱导现场钢轨波磨产生的振动频率相接近,且不稳定振动模态与实际线路波磨发生位置一致,因此轮轨系统产生摩擦自激振动可能是导致该区段低轨出现钢轨波磨的主要原因;同时不论是安装轨腰吸振器还是轨底吸振器都能明显缓解轮轨系统的摩擦自激振动,并且轨底吸振器与轨腰吸振器的减振效果相近。综上所述,安装轨腰和轨底吸振器均可抑制钢轨波磨的产生和发展。

对轮对-钢轨-吸振器系统进行了瞬时动态分析结果如图8。

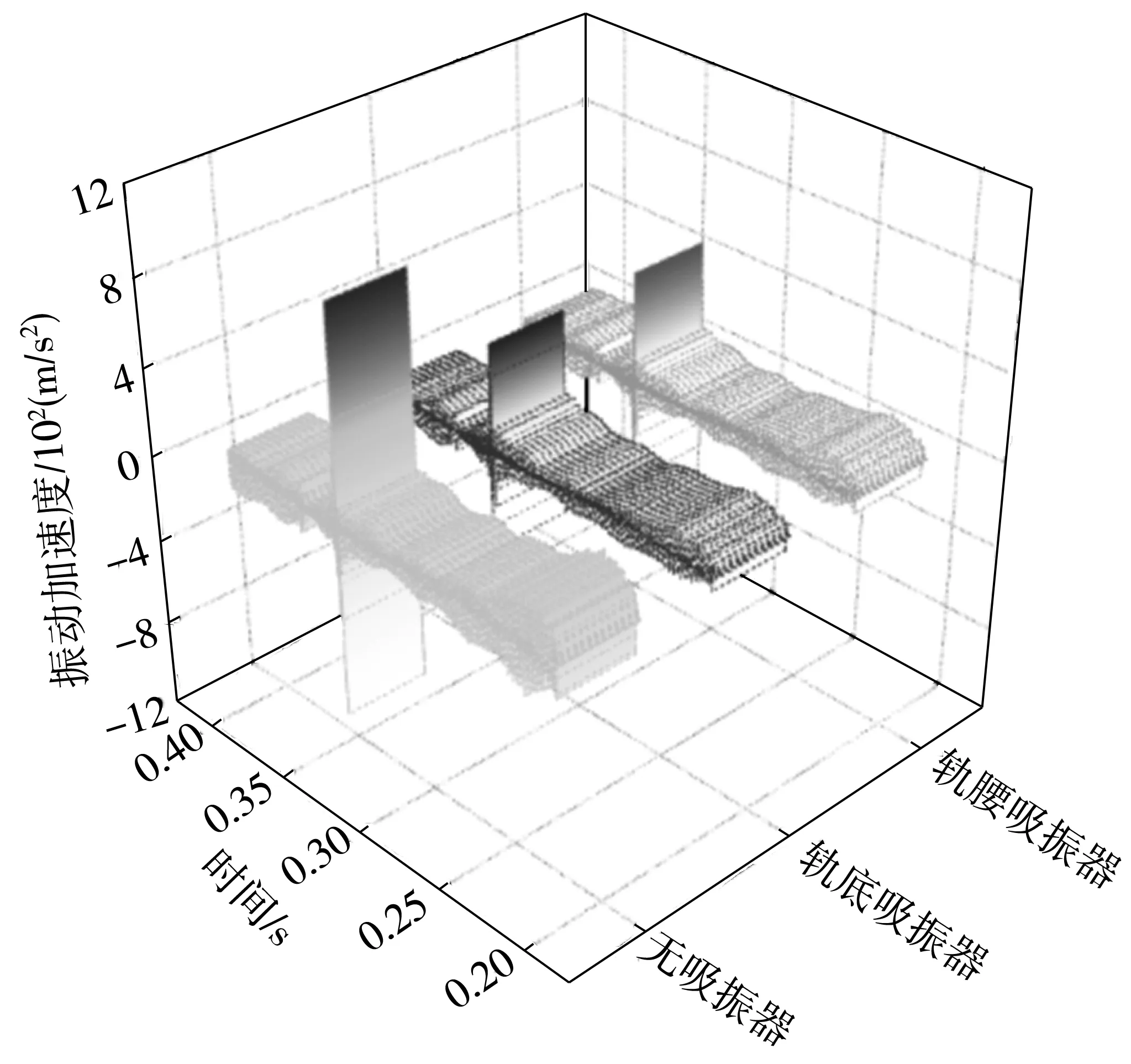
图8 附加钢轨吸振器前后瞬时动态分析Fig. 8 Instantaneous dynamic analysis before and after installing the rail vibration absorber

在未附加钢轨吸振器,当轮对以60～80 km/h匀速滚过轨面时,轮轨系统发生了剧烈的振动;当分别安装轨腰和轨底吸振器后,轮对-钢轨-吸振器系统的摩擦自激振动有大幅减小,且轨底吸振器与轨腰吸振器的效果很接近。时域分析结果显示:轨腰吸振器和轨底吸振器都能在很大程度减弱该系统的摩擦自激振动强度,进而抑制钢轨波磨的产生。

在轮对-钢轨-吸振器系统瞬时动态分析的基础上,进行了振动加速度的功率谱密度(PSD)分析,如图9。当轮轨系统未附加钢轨吸振器时,不稳定振动的主要频率为480.46 Hz,与上文复特征值分析结果(500.47 Hz)相接近;当附加了轨腰吸振器和轨底吸振器之后,轮对-钢轨-吸振器系统的摩擦自激振动强度显著减轻,其振动主要频率为474.86 Hz。

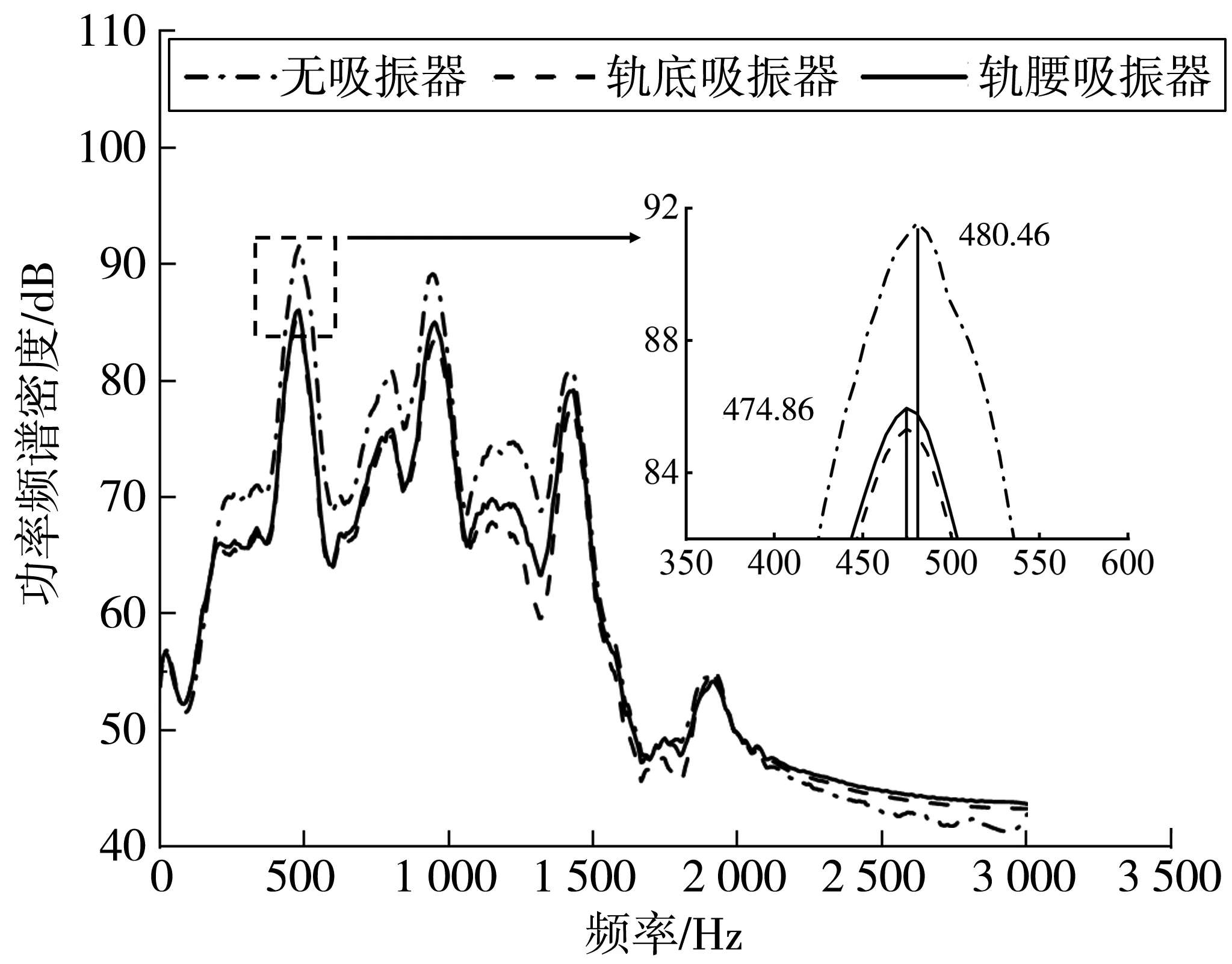
图9 功率谱密度分析Fig. 9 Analysis for power spectral density

为探明钢轨吸振器的吸振频段,笔者对轨腰吸振器的谐响应进行了分析[10],如图10。

图10中:当频率为480.95 Hz时,轨腰吸振器竖直方向的振动位移最大;吸振频率与轮对-钢轨系统摩擦自激振动的主要频率(500.47 Hz)非常接近。故认为轮对-钢轨系统的一部分振动被钢轨吸振器减弱,降低了轮对-钢轨-吸振器系统的振动强度。

图10 轨腰吸振器的谐响应分析Fig. 10 Harmonic response analysis of rail waist vibration absorber

结合以上3种分析结果发现:当未附加钢轨吸振器时,极易导致该区段钢轨波磨的出现;当附加轨腰和轨底吸振器后,轮对-钢轨-吸振器系统的摩擦自激振动强度大幅度减弱,且轨底吸振器抑制钢轨波磨效果略优于轨腰吸振器。

3.3 钢轨吸振器参数影响分析

合理设计钢轨吸振器的质量比、刚度和阻尼能使其吸振作用达到最优,进而更好地抑制钢轨波磨的出现与发展。为进一步探究轨腰和轨底吸振器对钢轨波磨影响规律,笔者讨论了这两种吸振器参数对轮对-钢轨-吸振器系统摩擦自激振动的影响。

钢轨吸振器质量比过大会引起钢轨静应力形变[16],过小则会加剧摩擦自激振动强度,故钢轨吸振器质量比变化范围为0.15～0.35,轨腰吸振器刚度范围为3～9 MN/m,阻尼范围为20～100 kNs/m[11],其结果如图11。

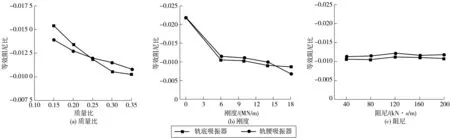
图11 钢轨吸振器参数对摩擦自激振动的影响Fig. 11 The influence of the rail absorber parameters on the frictional self-excited vibration

图11中:当轨腰吸振器和轨底吸振器质量比逐渐增大时,轮对-钢轨-吸振器系统的摩擦自激振动强度大幅度减弱;同样的,增大轨腰和轨底吸振器与轨道之间的连接刚度也能减弱该系统摩擦自激振动强度。当质量比达到0.25前,轨腰吸振器的减振效果优于轨底吸振器;当质量比增大到0.25之后,则效果相反。当连接刚度达到14 MN/m前,轨底吸振器的减振效果优于轨腰吸振器,连接刚度继续增大将出现与质量比变化相同的情况;随着轨腰和轨底吸振器与钢轨之间的连接阻尼逐渐增大,这两种吸振器对轮对-钢轨-吸振器系统的摩擦自激振动强度影响较小。因此增加轨腰和轨底吸振器与钢轨之间的质量比和连接刚度,能有效降低轮对-钢轨-吸振器系统的摩擦自激振动强度,有利于抑制和预防钢轨波磨产生。

4 结 论

笔者基于轮轨系统摩擦自激振动诱发钢轨波磨的观点,建立了车辆-轨道系统的动力学仿真模型,计算得出相应区段的动力学特性;通过建立轮对-钢轨-吸振器系统的有限元模型,对其进行了复特征值分析和瞬时动态分析;研究了轨腰吸振器和轨底吸振器对钢轨波磨抑制和预防的作用机理,以及这两种吸振器关键参数对该系统摩擦自激振动的影响规律。得出如下结论:

1)地铁车辆在通过小半径曲线区段时,轮轨间的蠕滑力将趋于饱和状态,这会导致轮轨系统发生摩擦自激振动,从而产生钢轨波磨,这种不稳定的振动主要出现在低轨处;

2)在短轨枕支撑小半径曲线区段的轨道上附加轨腰和轨底吸振器,轮轨系统发生摩擦自激振动的频率为480.46 Hz,且钢轨波磨出现频率与两种吸振器抑制振动的频率相重合,这说明轨腰和轨底吸振器均可对轮对-钢轨-吸振器系统产生的摩擦自激振动有一定抑制作用,从而预防钢轨波磨的出现和发展;

3)轨腰和轨底吸振器与轨腰之间的连接刚度和质量比对轮对-钢轨-吸振器系统的摩擦自激振动特性有显著影响。当质量比小于0.25和连接刚度大于14 MN/m时,轨腰吸振器减振效果优于轨底吸振器;反之,则轨底吸振器优于轨腰吸振器。故匹配合适的吸振器质量比、刚度和阻尼系数更有利于降低钢轨发生波磨的可能性。