枢纽机场中转衔接性的评估与优化

叶志坚,胡罗丹,高 伟

(中国民航大学 空管学院,天津 300300)

0 引 言

枢纽机场是民航发展的产物,指拥有密集航线、能为旅客提供高效、便捷中转服务的机场。“十三五”期间,全国千万级机场达到39个;按照规划,“十四五”期间将立足国内市场,构建完善的系统布局、高效运行的航空运输网络体系。我国在评估枢纽机场时多采用货运量、客运量等指标,但对中转衔接性这一指标的考虑也不可缺少[1-2]。

据OAG2010年数据,我国3大机场的中转比例只有10%左右,远低于公认的“枢纽机场中转比例应大于20%”这一标准[3],究其原因主要是我国是以“点对点”的发展模式所导致。E.O.MORTON[4]和金凤君等[5]均指出:在该模式下,距离短的两座机场会占据优势,但若只依赖于两个城市之间的运量,未从网络层次上对航线资源进行配置,故难以形成高比例中转的枢纽机场典型特征。随着交通流增长,航空公司逐渐意识到构建航线网络对于中转业务的重要性。近10年,支线机场通过邻近枢纽机场并联通全世界的格局逐渐形成,网络整体可达性增强,运行效率提高[6],但枢纽机场的航线网络互补性和中转衔接性仍有较大的改善空间,需要不断优化枢纽机场的航班时刻来实现。

K.G.ZOGRAFOS等[7]指出:航班时刻优化问题是在满足各类限制前提下对航班时刻进行优化配置,可最大限度满足各方要求,提高利用效率;LEE Sang-yong等[8]提出了衡量航空公司航班计划协调性的新指标——连续连接指数(CCI, continuous connectivity index),用来以提高航空公司航班时刻表的整体协调性;彭瑛等[9]建立了平均跑道延误时间最少、总时间调整最少、总延误航班架次最少的多目标航班时刻优化排序模型;L.COROLLI等[10]以尽可能减少时间调整偏移和预期运行延误总和为目的,提出了两阶段航班时刻的优化模型;I.SIMAIAKIS等[11]对长期航班时刻表进行了优化,从航空公司角度尽量减少了公司需求时刻和管理者分配时刻之间的差距;N.PYRGIOTIS等[12]基于一种需求平滑的优化模型和新网络排队论模型,对航班时刻进行了优化;A.JACQUILLAT等[13]研究了缓解繁忙机场拥堵问题的时刻调配手段和运行管理方法;N.A.RIBEIRO等[14]提出了一种基于优先级多目标航班时刻分配的模型及计算方法;K.G.ZOGRAFOS等[15]提出了一种同时考虑效率性和公平性的双目标时隙分配模型;K.G.ZOGRAFOS等[16]建立了考虑公平和效率的双目标优化模型,并采用ε-约束法和行生成算法来求解该模型;汪梦蝶等[17]基于可接受调整量水平,建立了航班时刻优化模型,并采用ε-约束法和改粒子群算法来求解该模型;徐晨等[18]提出了以国内航班效益最大化、国际航班中转效率最大化为目标,以空域结构、机场容量和航班连续性限制作为约束条件的航班时刻优化整数规划模型,并采用遗传算法寻求较优解;M.E.ÇIFTÇI等[19]提出了一种混合整数规划模型,基于模拟退火和禁忌搜索算法,优化了航空公司在其枢纽机场的航班时刻;J.DIANA等[20]提出了一种基于PSAM优化的决策支持工具,并通过优化模型对航班分配问题进行了分析;陈彬等[21]将航班总延误时间和航班总调整量作为目标,基于零和博弈的多目标线性加权法得到了最佳权重系数,并采用萤火虫算法(FA)对其求解;朱金福等[22]建立了以航班准点率、航空公司市场份额、旅客损失时间和航班功能定位指标最大化的航班时刻优化模型,并采用改进的粒子群优化算法进行求解。

现有研究多是基于航空公司立场对航班时刻表进行评估和优化,很少从枢纽机场角度来优化跨航司航班的时刻表,且现有研究对中转衔接命中数的评估和优化定义还不够严谨,特别是对中转衔接命中数优化中涉及到的影响因素分析不足,甚至衔接指数计算所需的某些数据收集困难,故从航班时刻优化理论和实践上很难有效处理并提升枢纽机场中转衔接命中数和其他影响因素的关系。

基于此,笔者对单一进港与总进港航班中转衔接命中数进行了定义,并对中转衔接命中数影响因素进行了分析,建立了最大化机场总中转衔接命中数的时刻优化调整模型和求解算法,并对机场总中转衔接命中数的相关性的影响因素进行了分析。

1 中转衔接命中数定义和计数法

中转衔接命中数是指进港航班在跑道容量和走廊口容量等限制情况下可衔接的中转航班数,分为单一进港航班的中转衔接命中数和可行时刻表的总中转衔接命中数。

单一进港航班中转衔接命中数指的是:时刻表上每一个到达航班在它可接受的衔接时间窗口内,考虑各种影响因素限制,能衔接到的所有起飞航班数,累加得到机场可行时刻表的总中转衔接命中数,即Ohits(original hits, 即初始中转链接命中评估数,也是初始未做时刻调整的中转链接命中评估数)。单一进港航班对应的离场航班所在时间窗口如图1。

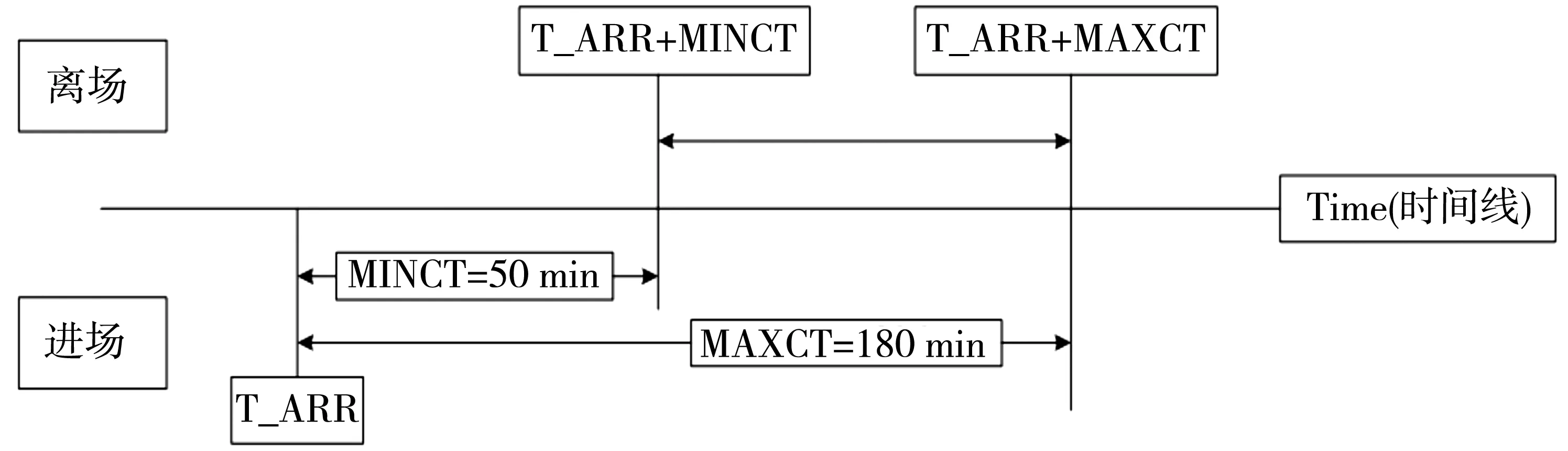
图1 单一进港航班可接受的出港航班所在的时间窗口Fig. 1 Acceptable time window of outbound flights corresponding to single inbound flight

对于某个到达航班,可接受衔接时间窗口是由航班最小衔接时间和旅客可接受最长等待时间构成,航班只能在此时间窗口内寻找合适的中转衔接航班。对于进港航班,假定最小衔接时间为50 min,旅客可接受最长等待时间为180 min;在这个时间窗口内某个离场航班与上述进场航班形成的中转线路绕航系数R≤1.25,则衔接命中数记为1,否则为0。重复考察所定义的时间窗口内所有离场航班与上述进场航班形成的中转线路绕航系数,就可得到单一进港航班中转衔接命中数。

单一中转衔接命中数高,就意味着某个到港航班有很大概率在有限时间窗内到达多个目的地,这暗示着该到达航班能吸引足够多的旅客到枢纽机场换乘,也反映了某个单独进港航班相对于其他航班的优势或劣势。

总进港航班中转衔接命中数等于所有进港航班衔接命中数的累加。机场总中转衔接命中数大小反映了机场潜在中转能力的强弱,潜在中转能力越强,对旅客吸引力越大,会产生积少成多、聚沙成塔的效应,从而使得枢纽机场竞争力增强。

2 中转衔接命中数影响因素

前述定义只用于评估某个机场某一次进港航班或全部进港航班在既有时刻表可衔接情况下的潜在衔接命中数,也就是假定按照所有进离港航班都能按计划时刻起飞降落去评估。在优化机场航班命中数时,所有影响进离港航班的可衔接性和准时起降因素都会影响衔接命中数,亦即评估和优化机场航班衔接命中数是不同的。评估机场衔接命中数只需考虑旅客中转可接受的时间窗口和绕航系数,而优化中转衔接命中数则需考虑如下因素。

2.1 绕航系数

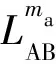
(1)

Rad过大会增加在空中的飞行时间,使得旅客行程时间增加,在存在更短行程的情况下,可能会抛弃经过B进行换乘。在优化过程中,尽量将与某个进港航班Rad≤1.25的离港航班配置在可接受的时间窗口内,将与该进港航班Rad>1.25的离港航班配置在可接受时间窗口外。

2.2 机场容量

机场容量是指在规定时间内,机场可处理航班的最大起降架次。

2.3 航班时刻结构

航班时刻结构是指一天或某个时间段内不同方向进离枢纽机场航班的时刻分布,对中转影响复杂而深远。合理的时刻结构会形成明显的航班波,能减少旅客等待时间、降低成本、提高航班配对率、提升机场中转潜力、增强城市连通性;反之,若航班时刻结构不合理,则可能会导致机场中转衔接性差、机场设施闲置或拥挤等。文中的航班时刻结构是在优化模型限制下,以最大化机场衔接性和最小化时刻调整量,通过自学习自动生成。

2.4 最小衔接时间

笔者主要考虑一架到达航班和其他执飞航班的衔接,只要离港航班过站活动完毕,到达航班的旅客即可从到达航班转机换乘到离港航班,因此这个时间比严格意义上的最小过站时间要短。由于本研究案例考察的机场为大兴机场,最近受疫情影响没有国际航班,故笔者考虑的最小衔接时间和最长旅客可接受中转等待时间均是国内转国内数据。根据大兴机场统计数据,平均最小衔接时间为50 min。

2.5 最长旅客可接受中转等待时间

3 总中转衔接命中数模型优化

为提升枢纽机场的衔接命中数,需要通过调整时刻结构来实现,同时要让给定时间段的航班进离港数量满足容量约束,从而消除计划产生的延误;调整过程中时刻结构应尽可能小,以减少对航司和航班耦合衔接机场的扰动。笔者构建了以最大化中转衔接命中数、最小化时刻调整量为目标,以无计划延误、跑道容量和走廊口容量为限制条件的双目标时刻规划调整模型,利用粒子群算法和线性规划联合求解,迭代出各种限制条件下的衔接性优化时刻表,提高枢纽机场的中转便利性和竞争力,为枢纽机场衔接命中数的影响因素相关性分析奠定基础。

3.1 时刻结构优化模型

模型总的参数定义如表1。

表1 优化模型中的参数设置Table 1 Parameter setting in optimization model

基本线性规划优化模型为:

1)决策变量

(2)

(3)

2)目标函数

(4)

(5)

3)约束条件

(6)

(7)

(8)

(9)

(10)

(11)

上述模型中,式(4)表示通过调整时刻表最大化中转衔接命中数,是模型的首选目标;式(5)表示在时刻调整过程中最小时刻调整量,是模型的次要目标;式(6)表示每个航班每天只能分配一个时刻;式(7)表示每个航班时刻允许调整量在一定范围;式(8)表示到达航班ma与起飞航班md经过B中转时的绕航系数;式(9)为机场最大容量约束;式(10)、 式(11)分别表示走廊口在时间片s的进离场最大流量约束。

3.2 算法求解

粒子群优化算法起源于对鸟群捕食行为的观察和研究。每只鸟被命名为一个没有质量和体积的粒子,多个粒子共存、合作寻优;每个粒子根据其自身以及群体经验,在问题空间中向更好的位置“飞行”。

本模型中笔者仅对初始时刻表在宵禁结束后(06:00—24:00)的航班进行调整,按照调整范围可分为两种:允许时刻最多调整30 min和允许时刻最大调整。分别计算得出正常调整中转链接命中数Nhits(normal adjustment hits)和最优化调整中转链接命中数Bhits(best adjustment hits)。其中:Nhits为允许时刻最多调整30 min,优化后中转链接命中数;Bhits为在允许时刻大调整下,最大化中转链接命中数。设置航班可选择起降的最小时间间隔为5 min,全天可划分成288个5 min,按区间可表示[1, 288],宵禁后可表示[72, 288]。允许时刻调整30 min(6个5 min),即航班以初始时刻E为中心,可向左或向右平移6个时刻,得到属于自己的调整区间[E-6,E+6];允许时刻大调整即航班可在[72,288]内在满足机场跑道容量限制和走廊口容量限制下任意挑选时刻。

以允许时刻调整30 min为例,求解算法流程图如图2。求解遵循两阶段法:先找到满足式(4)的候选解,然后在满足式(4)的多个候选解中挑出满足式(3)的解;将历史时刻表作为初始值输入模型,计算该时刻表的中转衔接命中数,得到初始中转衔接命中数Hmax。

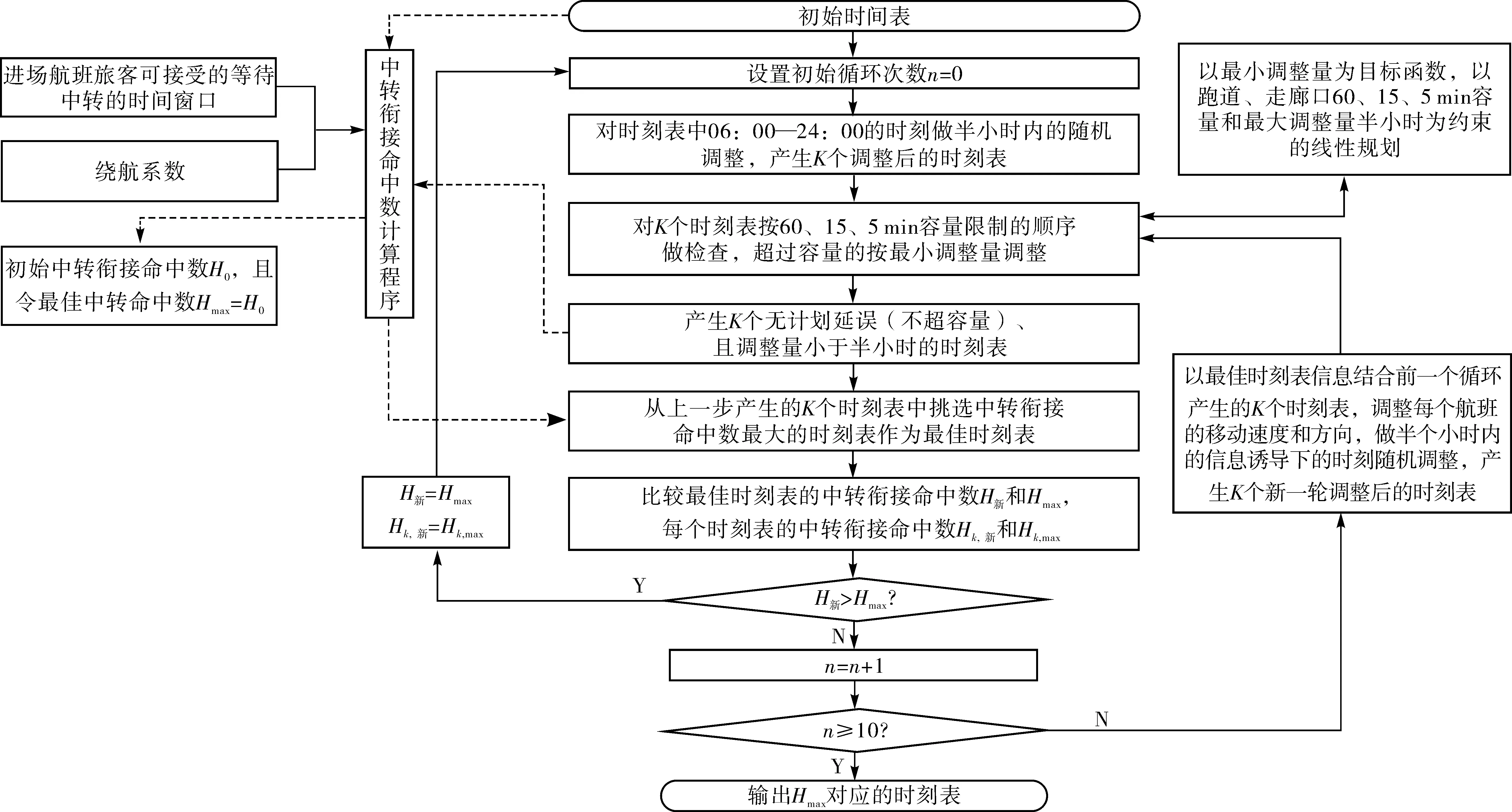
图2 模型求解流程Fig. 2 Model solving process

此时以最大化中转衔接命中数为目标,采用粒子群算法迭代产生新时刻表。在这些时刻表中,以时刻调整量最小化为目标,考虑绕航系数、机场容量、时刻调整的限制,选出符合要求的最优时刻表,计算该时刻表的中转衔接命中数H新,并与Hmax进行比较。若H新>Hmax时,令Hmax=H新,继续重复上述步骤产生新的最优时刻表,并计算它的中转衔接命中数H新,比较H新与Hmax,若H新>Hmax,则一直重复上述步骤,直至有10次(经多次重复实验证明取值10已满足精度要求),即连续10次都没得到更优化的中转衔接命中数,输出Hmax对应时刻表,即符合最大化中转衔接命中数、最小化时刻调整量的时刻表。

4 实例及优化效果分析

笔者以2020年5月1日所在一周的大兴机场航班计划时刻表数据为基础,用MATLAB计算程序评估了大兴机场初始的航班中转衔接命中数,然后分别以允许时刻调整量为30 min和不加限制这两种情况,利用时刻结构优化模型对大兴机场航班时刻进行调整,消除计划产生的延误并比较不同调整量下衔接效率的改善情况。

将大兴机场五一节所在周的时刻表作为输入,通过模型优化得到的结果如表2。由表2可知:中转衔接命中数与起降架次、航班允许调整时间成正相关变化。航班微调30 min,中转衔接命中数提高2%左右,而经无限制的大调整后,平均提高率高达36%,周三更是高达53%;由表2也可看出周三中转衔接命中数提高率最大。

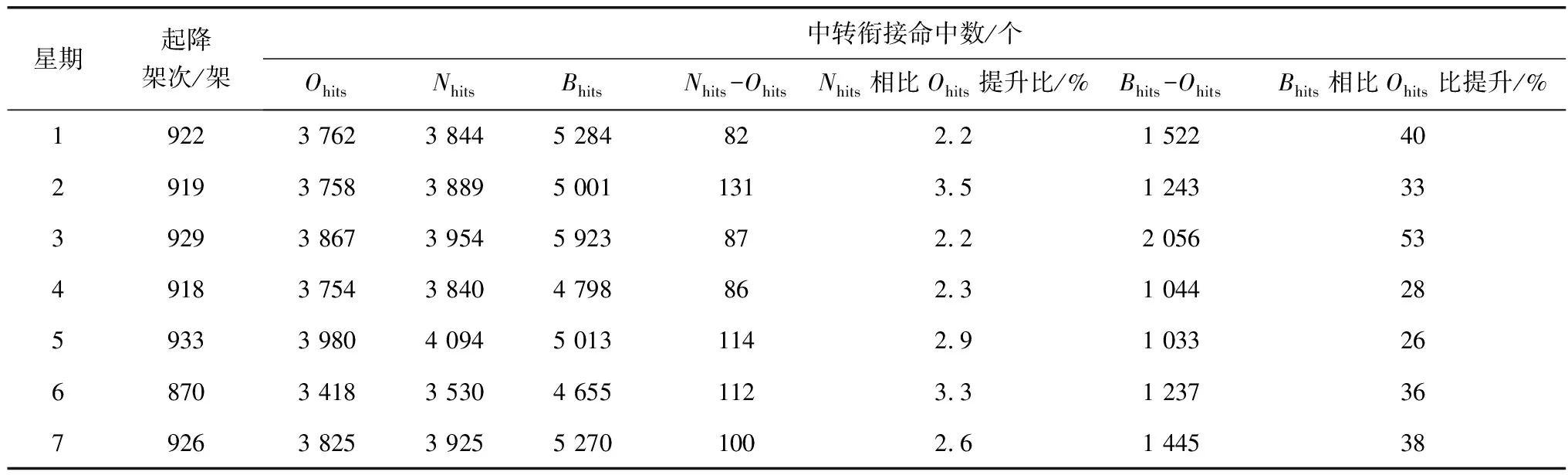
表2 大兴机场各类中转衔接命中数Table 2 Number of hits for various transit connections at Daxing Airport

时刻结构和衔接性关系如图3。图3中:横坐标为一天时间,以15 min为刻度进行划分,纵坐标是该15 min内的航班数,取正值为离场航班,取负值为进场航班。周三的Ohits时刻结构如图3(a),可以观察到没有明显的航班波,故Ohits较低;周三的Nhits时刻结构如图3(b),与图3(a)相比,图3(b)有了初步的波结构;周三的Bhits时刻结构如图3(c),可以观察到这时有了明显的波结构,说明中转衔接命中数大大提高。这表明:枢纽机场的中转衔接命中数和波结构呈正相关,波结构越明显,中转衔接命中数越大;同时也说明在优化过程中,让程序自学习生成衔接命中数大的航班时刻表会自动形成波结构。

在走廊口流量改善方面,各走廊口时段容量全部降低到预定水平,如A6走廊口优化前5 min流量变化如图4(a),走廊口5 min最大流量为8架次,超出规定的容量限制;优化后的5 min流量变化如图4(b),该走廊口5 min最大流量为4架次,符合容量限制要求,消除了走廊口超容导致的延误。

优化前后总的计划延误时间(在每个时间片安排的航班数量超过容量,将超过容量的航班往后顺延的时间总和)进行对比:优化前,按5 min容量8架次,周三的计划延误时间共11 310 min,平均每架次飞机延误12.17 min;优化后所有飞机计划延误全部消除并归于0。

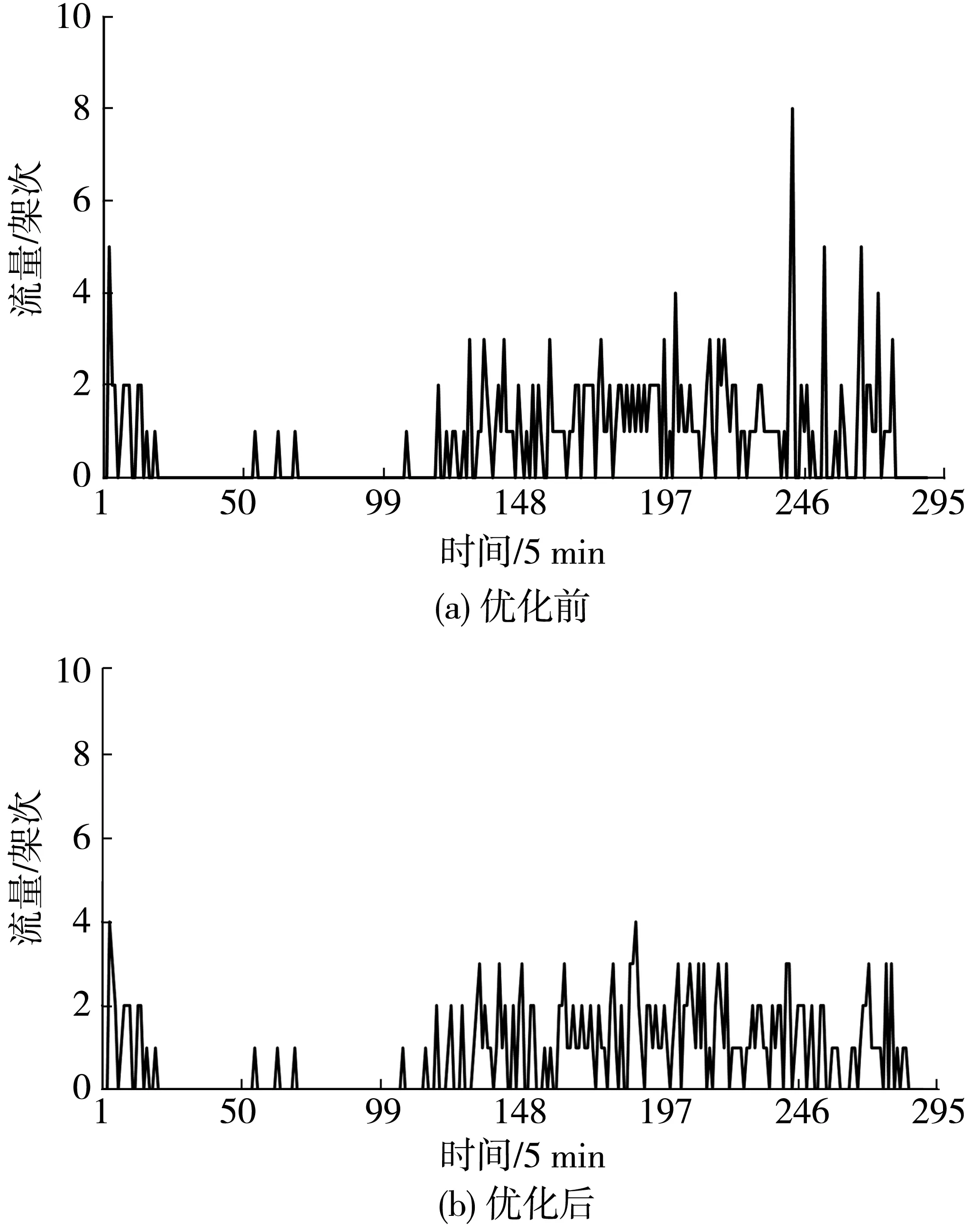
图4 优化前后A6走廊口5 min流量Fig. 4 5 min flow chart at A6 corridor entrance before and after optimization

为了说明蚁群算法的优化效果,列举了周三的Bhits随循环迭代次数的变化,如图5。在第113次循环获得最优解,再连续10次无提升,即循环次数到达123次时程序终止。计算周三的929个航班时间(包括出图时间和存储数据到Excel表的时间),获得优化时刻表需要约3.8 h左右。

综上,该结果表明所开发的时刻调整方法能有效消除因计划不合理导致的延误,同时优化后的中转衔接命中数有显著提高,可有效地提升旅客中转便利性。

图5 中转衔接命中数随循环迭代次数的变化Fig. 5 The variation of the number of transit connection hits changing with the number of loop iterations

5 数值模拟及相关性分析

为衡量各影响因素与中转衔接命中数的相关密切程度,采用数值模拟结合因素分析法进行分析。以起降架次为自变量时,其他参数保持不变,进行多次数值模拟;以允许调整时长、可接受时间窗口长度、绕航系数和机场容量为自变量时,其他因素保持不变,进行多次数值模拟。具体参数设置如表3。

表3 因素分析法中的参数设置Table 3 Parameter setting in factor analysis

图6(a)是大兴机场一周的时刻表,按表3参数设置将数值模拟得到的结果绘制成Nhits随起降架次变化图;图6(b)是以周三的时刻表为基准,按表3以允许调整时长为自变量,其他变量不变得到的Nhits随允许调整时长的变化图;图6(c)是以可接受时间窗口长度为自变量,其他参数不变得到的Nhits随可接受时间窗口长度的变化图;图6(d)是Nhits随绕航系数的变化图;图6(e)是Nhits随机场小时容量增长的变化图。

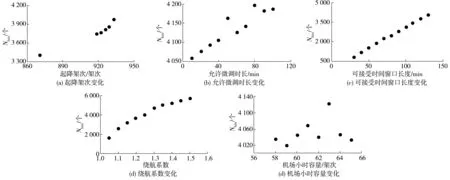
图6 周三的Nhits变化Fig. 6 Variation of Wednesday Nhits

为了得到Nhits与5个影响因素之间的相关关系,利用数值模拟结果计算了Nhits与5个影响因素之间的Pearson相关系数,计算结果如表4。相关系数从小到大排序为:可接受时间窗口长度、绕航系数、起降架次、允许微调时长、机场容量。排名前4的因素与中转衔接命中数均呈现出p=0.01的显著性水平,这说明中转衔接命中数与这4个因素之间有着显著正相关关系;而周三Nhits和机场容量之间的相关系数值为0.294 5,接近于0,并且p=0.479>0.05,说明这二者之间并没有相关关系。

计算5个影响因素之间的Pearson相关系数,具体计算结果如表5。由表5可知:各因素间相关系数都小于0.2,且p值全部大于0.05,这说明各因素间并没有相关关系。

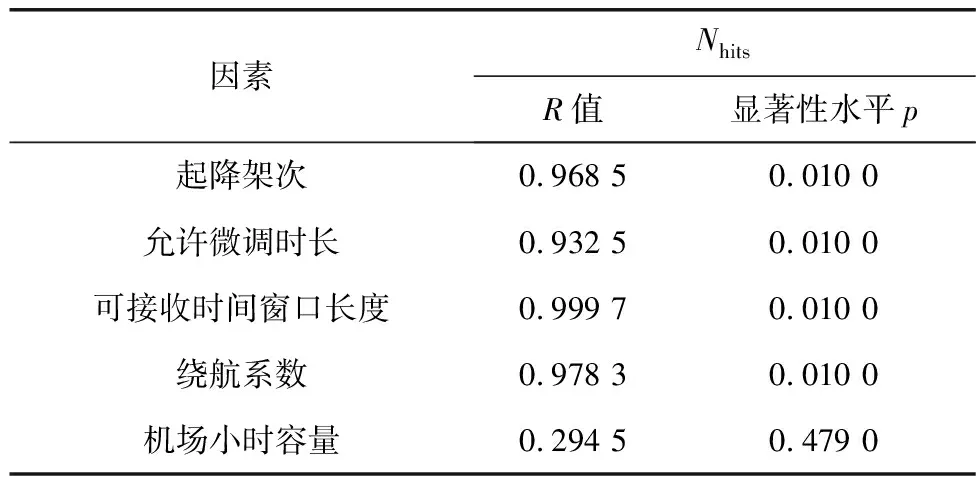
表4 Nhits与各因素的相关系数Table 4 Correlation coefficients between Nhits and various factors

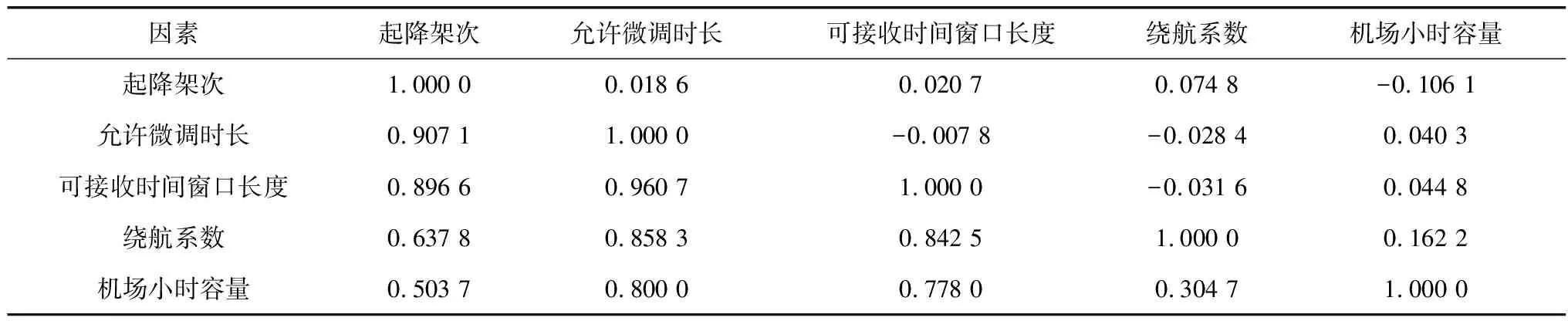
表5 各影响因素间的相关系数Table 5 Correlation coefficients among influencing factors

根据数值模拟结果合理设置可接受的时间窗口长度、起降架次、允许微调时长,充分考虑绕航系数,即可有效地提高中转衔接命中数。

6 结 语

笔者提出了中转衔接命中数的定义和计算方法,为不同机场间中转衔接性评估和比较提供了理论基础和操作可行性。提出了以中转衔接命中数最大化、时刻调整量最小化为目标的时刻结构调整模型,并以北京大兴机场时刻表作为初始数据进行了研究,研究结果表明:允许调整30 min最大化的中转衔接命中数比初始提高2.2%～3.5%;在不限制调整时长情况下,最大化中转衔接命中数比初始提高26%～53%。评估既有时刻表得到的命中数可能会高于实际的命中数,这是因为假定了时刻表是可行的时刻表;而优化得到的命中数是满足各种约束条件得到的命中数,比对原始时刻表评估的命中数更加合理,而且通过时刻调整,命中数都有提升。在假定各个机场时刻表延误相当情况下,用文中提出的命中数定义计算方法是合适的。

考虑到本场航班时刻调整会对目的地机场和始发机场的时刻产生影响,而目前的航班时刻编排裕度都超过30 min,因此认为调整30 min是可行的,无限制的本场时刻调整肯定不现实。尽管实际调整中无法一次达到满意效果,给大兴机场的策略建议为:让既有时刻表做30 min的微调提高衔接性,同时新增航班时刻尽可能按不限制调整时长所得最优时刻表中同方向的时刻排班,逐步提高机场中转衔接命中数;也可把新增时刻放到模型中去优化,旧的时刻允许调整30 min,新增时刻不限制调整。

由于实际旅客中转数据的缺乏,中转衔接命中数的影响因素还有待补充完善,笔者只分析了有限影响因素与潜在中转衔接命中数的相关性,其他与实际旅客中转有关的因素留待以后有数据后再深入研究;另外,笔者仅研究了进港航班中转衔接命中数,对于离港航班是否可类比计算,仍需探讨。