含石量对土石回填体渗流特性影响的试验研究

黄 锋,杨正旭,周启宏,刘星辰,张 班

(1.省部共建山区桥梁及隧道工程国家重点实验室,重庆交通大学 重庆 400074; 2.重庆交通大学 土木工程学院,重庆 400074; 3. 中铁二十局集团第三工程有限公司,重庆 400065)

0 引 言

随着我国西部开发与“一带一路”战略的加速推进,西南山地城市交通基础建设取得了突飞猛进的发展,重庆作为典型的山地城市,基础建设的发展必须以开山填谷的方式打破复杂地形条件的制约,因此在城市浅表地层以深厚土石回填体为主。不同于常规均质岩体与土壤,土石回填体大都由体积离散性强且形态不规则的岩块与黏土混合而成。受施工粗糙与监管疏忽的影响,多数回填体土石级配不良,其渗透性特性难以把握[1-4]。因此,西南多雨气候条件下土石回填体隧道与基坑的防水、加固工艺的改良一度成为施工建设单位的难题。

早期学者大多针对土的渗透特性开展了系列研究[5-7]。其中,太沙基等[5]针对粗粒土提出的渗透系数经验公式(1)受到广大研究者的认可;中国水科院刘杰[6]在太沙基经验公式(1)的基础上加大了土颗粒控制粒径范围,对粗粒土渗透系数经验公式进行了改进,如式(2);朱崇辉[7]通过引入不均匀系数及曲率系数对太沙基经验公式(1)进行了改进,如式(3):

(1)

(2)

(3)

式中:k为粗粒土的渗透系数;k10与k20分别为水温10 ℃与20 ℃时的粗粒土渗透系数,cm/s;e为孔隙比;d10与d20分别为土颗粒的有效粒径,即土体粒径级配分布曲线上颗粒粒径占比10%与20%所对应的土颗粒粒径,cm;R为与其它未知因素的相关系数,可通过数据拟合获得;Cu为不均匀系数;Cc为曲率系数,可根据土体颗粒有效粒径计算获得。

随着非均匀性颗粒介质的渗透理论的发展,围绕着砂土、砂砾等离散性大且黏聚力差的非均匀基质渗透水特性研究不断涌现出大量成果。苏立君等[8]利用相关性分析方法针对天然砂土渗透系数提出经验计算公式(4);梅世昂等[9]则通过一系列渗流试验研究,得出了砂砾土的渗透系数经验公式(5)。可见,多数研究通过选取合适的粒径来表征整体砂土的粒径。

(4)

(5)

式中:C为无因次系数,可取为157;n为孔隙率;P5为砂砾土中细颗粒的含量;d0为颗粒的控制粒径,cm。

考虑到黏土与粗粒土间的渗透系数差异主要是由黏土结合水占据大量的渗流孔隙,而使基质内部渗流通道减少所致。因此,在计算黏土渗透系数过程中,为了排除结合水对孔隙比参数的影响,需将黏土基质中结合水占据孔隙体积与土颗粒体积之比定义为无效孔隙比,而有效孔隙比则由总孔隙比与无效孔隙比作差获得。基于此,党发宁等[10]与杨忠翰等[11]通过渗透试验及有效孔隙比测试分别得到了黏性土与红、黄黏土的渗流系数经验公式如下:

(6)

k=10-7(3 442e4-12 923e3+18 124e2-11 245e+

2 603)

(7)

式中:eu为有效孔隙比;e0为无效孔隙比。

鉴于土石混合体级配构成与介质体积、形状的非均匀性,其物理力学性质也因此极为复杂,渗透特性也不同于均质黏性土与规则砂砾料[12]。常规土体、砂砾等单一基质材料的渗透系数经验公式对土石混合体并不适用。因此,周中等[13]考虑土石混合体渗透特性的影响因素,基于土体与砾石的独立渗透系数及相互影响机理,采用幂平均法提出土石混合体渗透系数经验公式(8):

k=[P5(kG)f+(1-P5)(kS)f]1/f

(8)

式中:kG为砾石的渗透系数,cm/s;kS为土的渗透系数,cm/s;f为无因次系数,可以通过少量试验回归分析确定。

综上所述,渗流介质构成、颗粒级配及有效孔隙比等参数均是影响黏土、砂土、砂砾、土石混合体渗流特性的主要因素,多数研究基于渗透试验利用经验公式对介质渗透系数进行表征。针对均质单一介质的渗透特性的研究较多且结论成熟,而对于土石颗料粒径级配不良、尺寸形状不均的土石混合体渗透特性的研究较少。考虑到土石回填体中含石量对渗透性能影响显著,且既有经验公式的适用性难以把握。因此有必要针对土石回填体渗流特性的含石量敏感性开展常水头试验,对比分析土石回填体的渗透系数响应趋势与细颗粒流失规律,并对应给出渗透系数的经验拟合公式,可为土石回填土含石量的控制及地层加固工艺的优化提供参考与借鉴。

1 大粒径土石回填体常水头渗透试验

1.1 土石回填体工程特征与样品制备

工程土石回填体取自重庆轨道交通10号线二期兰花湖停车场基坑与出入段隧道土建施工现场。现场地表土石回填体地层深厚且处于欠固结状态,土石回填体强度通常受区域性地表强降水及地下水迁移的影响而发生弱化。现场土石回填体地层在降水入渗与施工扰动共同作用下极易出现地表塌陷、基坑边坡滑塌、隧道掌子面变形等施工问题,施工期间多通过地表注浆对软弱地层进行加固,同时利用基坑井点降水与掌子面帷幕注浆止水等工艺对工区范围内地下水进行引排与堵截。室内试验及现场灌水法测得土石回填体相关的基本物理参数见表1。

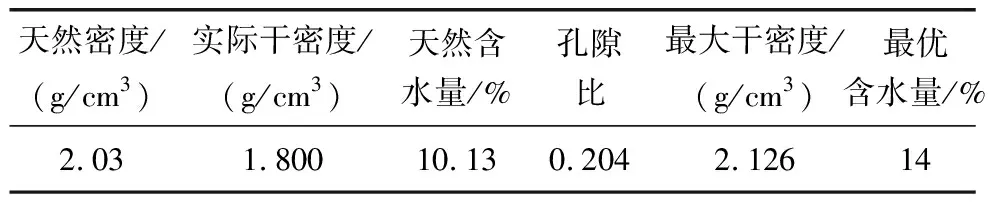
表1 土石回填体基本参数Table 1 Basic parameters of soil-rock backfill

首先将现场获取的工程土石回填体粗略筛分为两部分:0～5 mm的细颗粒土与5～60 mm的粗颗粒块石。随后,并按照0%、20%、40%、60%、80%、100%的粗颗粒块石的掺混比例(含石量v)进行混合。为了检测试验样品的颗粒级配,再次针对掺混后的土石回填体进行筛分与称量统计,获得不同含石条件下土石回填体的颗粒级配曲线如图1。随着土石回填体含石量的增加,粗颗粒增多而细颗粒减少,因定义细颗粒土与粗颗粒块石的界限为5 mm,故含石量0%的土石回填体内无大于5 mm的粗颗粒,而含石量100%的回填体内则无小于5 mm的细颗粒。综上所述,通过原状土石回填体的粗略筛分混合而成土石混合体满足常水头渗透试验样品的级配要求。

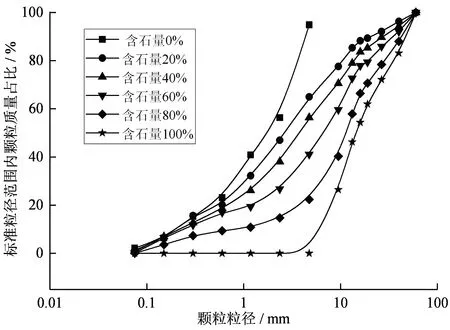
图1 不同含石量样品的级配曲线Fig. 1 Grading curve of samples with different stone contents

1.2 土石回填体常水头渗透试验方案

针对土体常水头渗透试验,GB/T50123—2019《土工试验方法标准》中规定圆筒内径须大于土体颗粒直径的10倍。周中等[13]采用自制常水头渗透试验仪开展测试期间,按照规范要求仅将基质最大粒径控制在2 cm。可见,为了满足大粒径土石回填体常水头渗透试验规定,对试验仪器尺径提出更高要求。因此,依据实际工程背景笔者采用LDST-300粗粒土常水头渗透仪(图2)对大粒径土石回填体渗透系数进行测定,该设备主要由供水箱、试样桶、测压管和集水槽四部分组成,刚性试样桶内径为300 mm,高为500 mm,设备满足TB10751—2018《高速铁路路基工程施工质量验收标准》最大粒径不大于75 mm的粗粒土的常水头渗透试验要求。

图2 试验装置示意Fig. 2 Schematic diagram of test device

为了分析含石量对土石回填体渗透特性的影响,考虑土石回填体中块石含量(颗粒粒径大于5 mm属于块石颗粒),设计6组常水头试验工况,如表2。

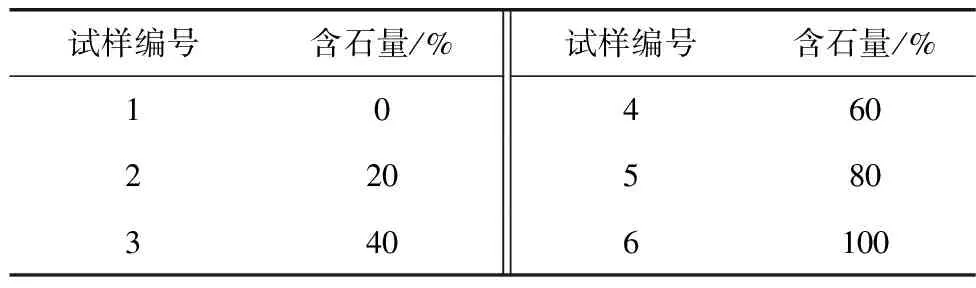
表2 试验方案Table 2 Test scheme

常水头试验步骤大致如下:

1)工程土石回填体取回后需进行烘干、筛分等工作,确定土石级配。随后将筛分样品分为颗粒尺寸为0～5 mm的土颗粒与块体尺寸为5～60 mm的块石两部分,控制工况设定含石量配置试验样品并均匀拌合。

2)试样桶装样前需在内壁均匀涂抹凡士林减小摩擦阻力带来的试验误差。随后将试验样品分10层装入,并对层间接触面进行凿毛处理,控制分层厚度为特征粒径d85的1.5～2倍(即层厚50 mm),依据初始干密度1.8 g/cm3,将试样分10层装入圆筒内,基于实际情况结合相关文献[12,14]结论,统一控制不同含石量试样压实度为0.8,固定落距为40 cm,使用质量为9 kg,直径100 mm的击实锤进行试样击实,控制击数实况为98次,共计击实能量为987.84 kJ/m3。击实锤压实期间采用环刀取样进行压实度抽样检测,每层试样装填合格后,开启试样筒底部进水管对试样自下向上逐渐浸润至饱和后关闭。

3)随后,将供水管接入试样筒顶部注入试样筒内,降低调节管至试样靠上1/3高度处,形成水位差,使水渗入试样后经调节管流出。随后保持试样筒内水位不变,使试样处于常水头环境下进行渗透,待测压管水位稳定后,记录各测压管水位差,同时测量记录集水槽自调节管口接取渗透水的体积与进水管的水温。随后分别降低调节管至试样的中部与下部1/3处改变水力坡降进行重复测试,最后计算3次测试渗透系数的平均值。

2 土石回填体渗流特征含石量敏感性分析

2.1 土石回填体渗透系数含石量敏感性分析

基于土石回填体常水头渗透试验数据,可通过式(9)计算获得试样渗透系数(k20),并利用平均处理方法对3次试验结果进行统计见表3。可知,土石回填体标准渗透系数随含石量的增加而迅速增长。

(9)

式中:Q为时间t内渗透水量,cm3;L为装填试样高度,cm;H为平均水位差,cm;t为时间,s;A为装填试样横断面面积,cm2;ηT为水在水温T下的动力黏度,10-6kPa·s,试验水体温度约20 ℃;ηT/η20为效正系数。

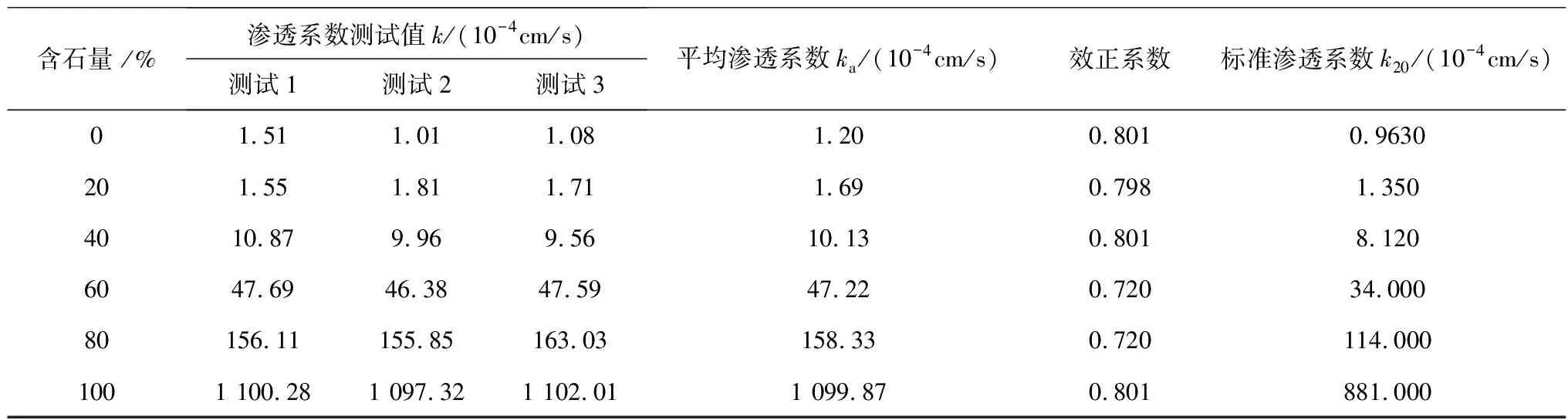
表3 土石回填体常水头渗透试验结果Table 3 Results of constant head permeability test of soil-rock backfill

基于周中等[13]对土石混合体中含石量与渗透系数关系的研究结论,发现笔者研究对象(最大块石粒径为60 mm的土石回填体)的含石量与渗透系数之间同样满足显著的指数关系,如图3。在试验数据及规律合理的基础上,观察到最大块石粒径为60 mm的土石回填体渗透系数随含石量增加而增大过程中,含石量为60%可作为渗透系数指数增长的拐点,当含石量大于60%时,土石回填体渗透系数增幅显著增大。与周中等[13]所用试样不同,笔者采用的土石回填体试样颗粒级配中粒径<1 mm的细颗粒少,而粒径>5 mm的颗粒多,使得介质的渗透性因孔隙度的增大而变差,而块石的形状与磨圆度对介质的渗透性也存在一定程度的影响。

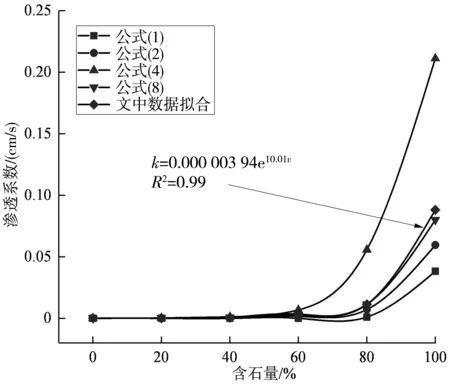
图3 经验公式计算结果Fig. 3 Calculation results of empirical formula

为了探究土石回填体渗透系数经验公式的适用性,选取前文提到的具有代表性的公式(4),公式(8)对笔者试验结果进行计算比对。可见,土石回填体含石量较低时,计算结果较接近,而当含石量>60%时,除了周中公式外,其他经验公式计算结果差异性逐渐显著,这主要与试验样品与方法不同有关。其中,公式(1)与公式(2)只单独考虑了土的渗透系数而计算结果偏小,更适用于小颗粒均匀土体渗透系数的计算;公式(4)因考虑了不均匀系数与曲率系数而计算结果偏大,更适用于砂砾土的渗透系数计算。而文中最大块石粒径为60 mm的土石回填体试验数据与公式(8)的高度拟合则说明了公式(8)的适用范围与试验的合理性。

2.2 土石混合体细颗粒流失量化分析

土石回填体常水头渗透试验期间,集水槽中的水逐渐由浑浊变为清澈,说明土石回填体内细颗粒随水体迁移与渗透发生流失。对比试验结束后试样的土体流失情况如图4。可见,在含石量较低时(0%～20%),土石回填体试样仅局部出现小区域土体流失,呈法向倾斜分布,试样成型较好。含石量增至40%时,试样土体流失区域有所扩大,呈法向条形分布,表面露出少量粗颗粒,试样成型良好。含石量继续增大(60%～80%),试样土体流失区域扩大并由法向条形向环向扩展贯通呈片,表面大量粗颗粒外露,试样基本成型。含石量为100%时,试样缺少细颗粒的黏聚,仅靠粗颗粒骨架难以成型。综上所述,常水头渗透作用下土石回填体细颗粒的流失量及流失范围均随含石量的增加而增大,土石回填体成型能力也因块石占比的增加而变差。依此可见,土石回填体地层中细颗粒土在降雨入渗及地下水迁移作用下发生流失是地层失稳、塌陷灾害的主要诱因。

控制集水槽内浑浊液体细颗粒的2次沉降、收集、烘干、称重的间隔为5 min,分别绘制6种土石回填体试样细颗粒流失量随渗透时间的变化曲线,如图5。细颗粒土的累计流失量随渗流时间的延长由小变大并在最终趋于平稳,而细颗粒流失速度(曲线斜率)随渗流时间的延长呈现出先增大后减小的规律。结合图4揭示的土石回填体试样透水形态变化分析可知,常水头渗透试验期间,试样粗颗粒所占比重随细颗粒流失量的增加而增大,因此在渗流试验前期(约30 min)内,细颗粒流失速度存在由小到大的变化,而试验后期细颗粒流失速度由大到小变化主要是试样内部细颗粒流失殆尽所致。

图4 不同含石条件下透水试样土体流失及成型状态Fig. 4 Soil loss and forming state of permeable samples under different stone content conditions

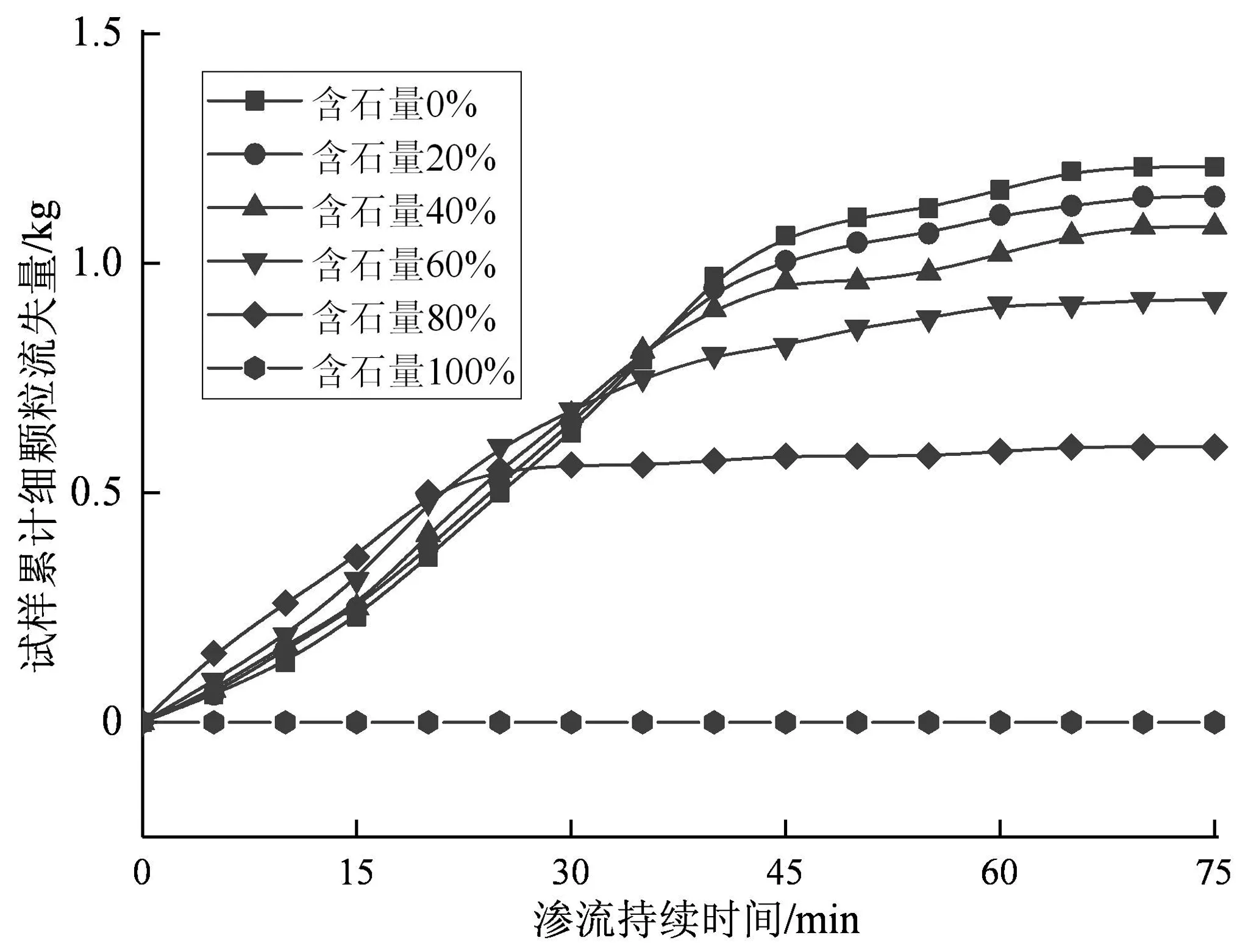
图5 不同含石条件下透水试样细颗粒流失时程曲线Fig. 5 Time history curve of fine particle loss of permeable samples under different stone content conditions

定义试样中细颗粒流失量占比C为土石回填体试样中细颗粒在渗流作用下累计流失质量ml与土石回填体试样中初始掺入细颗粒质量ms之比,如图6,拟合为经验公式为:

(12)

式中:ml为流失土体质量;ms为土石回填体中土的质量;v为含石量。

土石回填体内细颗粒流失占比与材料含石量呈指数正相关的原因主要有两方面,一方面是前文所述大量块石的掺入形成粗颗粒骨架,介质渗透系数随孔隙率的增大而增大,进而加快了自由水迁移带走细颗粒的速率;另一方面则是土石回填体中块石粗颗粒骨架与细颗粒土的黏聚性下降,自由化渗透路径固定且粗颗粒表面细颗粒附着率低,导致大量轻质细颗粒流失。

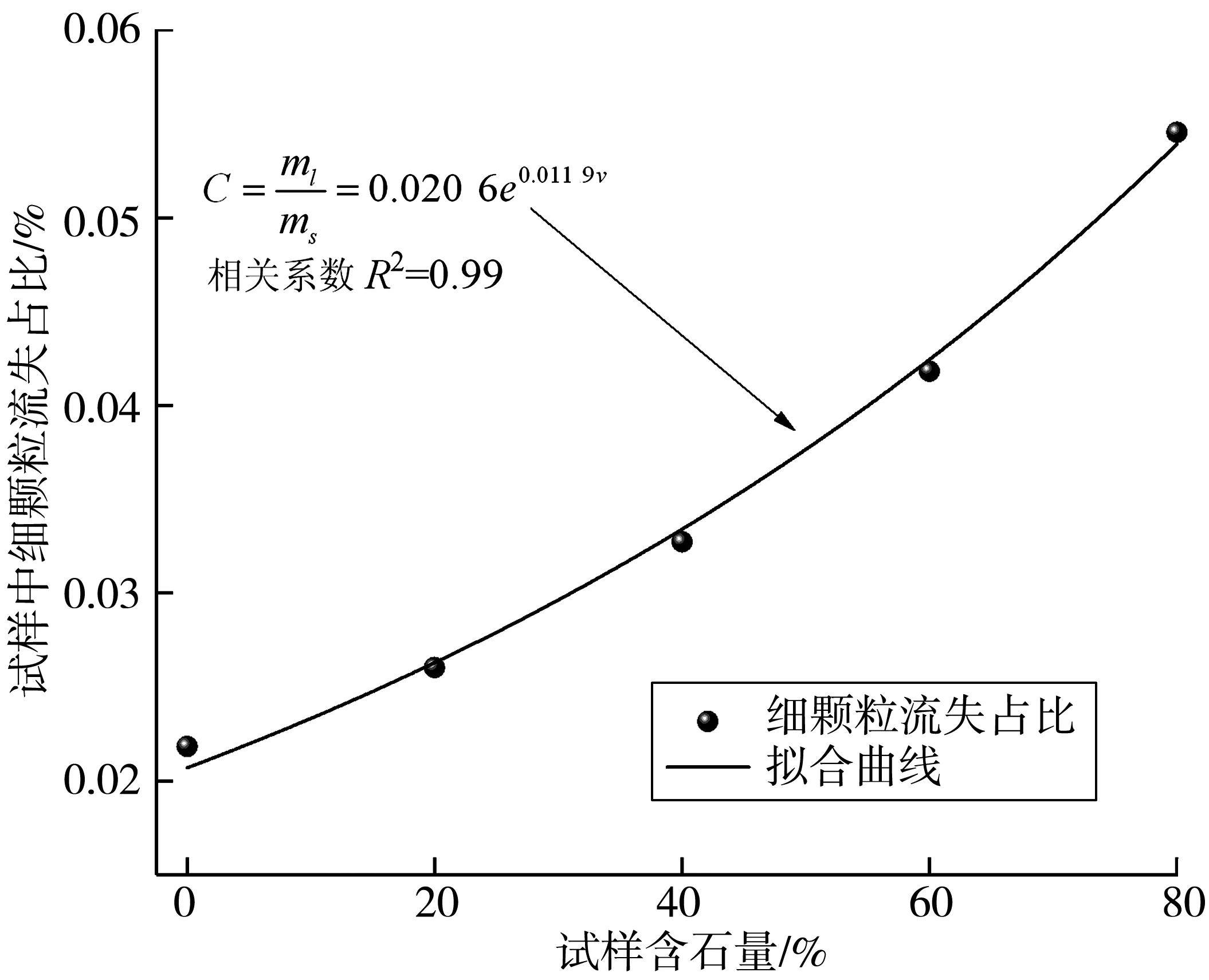
图6 不同含石条件下细颗粒累计流失占比Fig. 6 Proportion of cumulative loss of fine particles under different stone content conditions

3 结 论

以在建工程工区地层的土石回填体的渗透水特征与地层加固工艺为背景,基于回填体的真实含石量与颗粒级配,于实验室内完成了最大粒径为60 mm下不同含石量土石回填体常水头试验研究,得到了如下3点主要结论,可为土石回填土体地层的注浆加固工艺与截排水措施优化提供参考。

1)大粒径土石回填体渗透系数随含石量的增加呈指数形式增长,当含石量大于60%时,土石回填体渗透系数增幅显著增大。土-石回填体渗透系数经验公式的参数优化应综合考虑细颗粒土体与粗颗粒块石的综合影响。

2)土石回填体渗流作用下细颗粒的累计流失量随渗流时间的延长呈现小-大-平稳的过程,而流失速度则呈现出先增大后减小规律。土石回填体内细颗粒流失与材料含石量呈指数正相关。

3)颗粒级配不良的土石混合体中粗颗粒骨架间孔隙是自由水迁移与渗流的主要通道,而细颗粒的黏聚性及表面附着性不佳是土体流失关键因素。