三峡库区浅水域船舶应急系泊系统设计及水动力特性研究

袁培银,张 哲,李渝锋

(重庆交通大学 航运与船舶工程学院,重庆 400074)

0 引 言

长江通道在我国实施西部开发、中部崛起和东部率先的区域发展战略中具有十分重要的战略地位。长江航务管理局制定了新时代长江航运发展的新规划:要以新时代建设社会主义现代化强国目标和交通强国战略部署为根本指引,全方位实现长江航道航运现代化,全方位立体化建设长江全流域黄金水道。三峡库区水运航道建设日新月异,且内河船舶逐渐趋向大型化、标准化、专业化。然而,三峡库区在夏季容易发生强风、暴雨且常常伴有雷电的极端天气,连续暴雨往往会导致库水位的上升、山体滑坡、泥石流等自然灾害,三峡库区浅水域船舶往往采用应急系泊的方法来规避这类极端天气。因此,对三峡库区浅水域系泊状态下的船舶进行水动力特性分析和系泊缆张力变化规律研究至关重要。

目前,国内外专家学者针对船舶系泊系统水动力性能所开展的研究大部分是通过计算机数值模拟和物理模型试验两种方法。在数值模拟方面,I.TOUZON等[1]基于运动学方程,对支撑结构和系泊系统之间的相互作用进行模拟求解。该研究选择采用悬链线系泊系统,并在考虑实际海况的情况下进行耦合模拟。研究结果表明:风浪流的叠加作用是导致莫里森系数和系泊缆绳张力变化的主要原因;肖力旗等[2]研究不同装载状态对船舶六自由度 RAO(幅值响应算子) 和运动量的影响规律,发现横摇幅值和固有周期随船舶装载量的增大而增加,同时也将降低船舶稳性。并且缆绳断裂的可能性会随着装载量增大而增大;沈文君等[3]利用数值模拟方法,得到了各个护舷在不同浪向角作用下受力特点和规律,计算结果表明:浪向为斜浪时,各个护舷的受力相差较大,迎浪侧护舷受力最大,中间的护舷受力最小;高峰等[4]研究风浪流复合环境条件下不同船型的船舶在系泊状态时船舶的六自由度运动响应及系泊缆顶端张力的变化机理,研究表明系泊船舶的运动情况、缆绳张力和撞击力与所处环境的波高、波浪周期呈正相关,其变化幅度与不同船型本身的固有周期有关;陈浩[5]利用 ANSYS 软件分析研究开敞式码头结构的动力特性,发现码头结构的固有频率会随着不同的水位工况而发生改变;李宁等[6]基于悬链线理论,以单点系泊系统静力学模型为研究对象,解决了系泊系统在不同环境载荷和锚链规格情况下的系泊重块和各部分钢管与浮式结构物之间的夹角、锚链几何外形和基本参数、浮式结构物的吃水深浅和活动范围的优化设计问题;董胜等[7]设计了一种首尾两点系泊系统,研究油船与系泊系统耦合条件下的运动响应以及缆索张力的变化规律。

在物理模型试验方面,杨国平等[8]在理论分析的基础上,加以物理模型试验研究船舶装载量不同、浪向角不同、码头长度不同以及系泊缆与船舶夹角不同的系泊状态下的船舶缆绳张力和撞击能量半经验半理论计算公式;朱奇等[9]通过物理实验,分析研究风、浪、流共同作用下码头泊位长度与缆绳布置方式对系泊船舶六自由度运动响应和系泊缆绳顶端张力的影响;郭士勇等[10]采用理论结合模型试验的分析方法,研究横浪作用于系泊船舶的撞击能量规律,并结合物理模型试验进行数据拟合,得到完整的系泊船舶撞击能量估算公式;史宪莹等[11]通过物理模型试验研究涌浪和风浪同时出现时,系泊船舶的六自由度运动响应规律;王志斌等[12]通过理论设计、仿真计算及模型试验的方法,提出在风浪流环境下某特殊船型的码头系泊模式优化方案;嵇春艳等[13]基于传统的张紧式系泊方法,提出在系泊缆的末端等距布置质量块的新型深水浮式平台系泊系统,改善浮体的低频运动响应,约束了浮体的偏移;王秋玲等[14]基于浮筒式防风单点系泊系统,通过MATLAB模拟仿真技术提出一种选择锚链与浮式结构物夹角、锚链外形及参数、系泊块重量、浮式结构物吃水深浅的有效方法。

沿海的大型港口码头系泊下船舶的水动力性能研究已经日趋成熟完善,但对于三峡库区浅水域船舶应急系泊研究还存在一定短板。笔者采用数值模拟的方法,研究不同系泊状态时内河船舶在风、浪、流等复杂环境下运动响应以及缆绳张力变化特性,研究结果和研究方法可为内河浅水域船舶系泊安全提供理论支撑,对提高内河船舶系泊作业安全和港口作业效率有一定的参考价值。

1 计算理论

1.1 三维势流理论

在三维势流理论中,假设理想流体是均匀的、不可压缩的,且无粘性因素影响,则可以通过引入速度势φ(x,y,z,t)来描述流域内的运动[15]。当浮式结构物以自由面为基准时,速度势满足Laplace方程:

∇2φ(x,y,z,t)=0

(1)

为了描述物体运动的速度势以及Laplace方程,需要对其进行线性化处理。在线性化处理中,假设波浪运动和浮式结构物的运动幅度都很小。此外,在流场中速度势可以分解为入射波速度势、绕射势和辐射势。

φ(x,y,z,t)=φI(x,y,z,t)+φD(x,y,z,t)+

φR(x,y,z,t)

(2)

式中:φI为入射波速度势,表明流场中速度分布的情况;φD为绕射势,表明结构物对流场内的速度产生的影响;φR为辐射势,表明浮式结构物六自由度的运动和振荡对周围流场的影响。

1.2 系泊缆力计算方法

根据静态悬链线理论,可推导出在稳态下缆绳的载荷与系统平衡状态、锚链几何形状以及张力分布之间的关系。为了简化计算,通常忽略环境载荷、缆索的弹性伸长以及本身动力效应的影响,并按照悬链线理论进行计算[16]。

图1中,风、浪、流作用于船体,并通过锚链传递给锚泊系统。以xoz为坐标系,根据力的平衡,在锚链系微元的切线和法线方向上分别有方程:

(3)

(4)

(5)

(6)

式中:T为锚链线单元下端张力;w为锚链线的单位湿重;h为水深;s为悬链长度;φ为锚链线单元与水平面的夹角。

锚链线与海底有接触部分,φ=0,推导:

(7)

(8)

将z=h代入式(8):

H=T-wh

(9)

(10)

(11)

V=wh

(12)

式中:H为锚链线沿水平方向分力;V为锚链线沿垂直方向分力;xmax为x的最大值;smax为s的最大值。

2 频域分析

笔者基于三维势流理论,利用 ANSYS 建立船舶湿表面有限元模型,运用 AQWA 模块对船舶进行水动力性能分析,得到水深5 m,浪向角为90°时,船舶六自由度幅值响应算子,并分析幅值响应算子与波浪周期的变化关系。

2.1 模型建立

坐标系原点位于船头,X轴由船艏指向船艉为正方向,反之为负方向;Y轴由左舷指向右舷为正方向,反之为负方向;Z轴以水面向上为正方向,水面向下为负方向。规定环境载荷作用角度是与X轴负半轴的夹角逆时针为正,反之为负。具体的坐标系定义如图2。

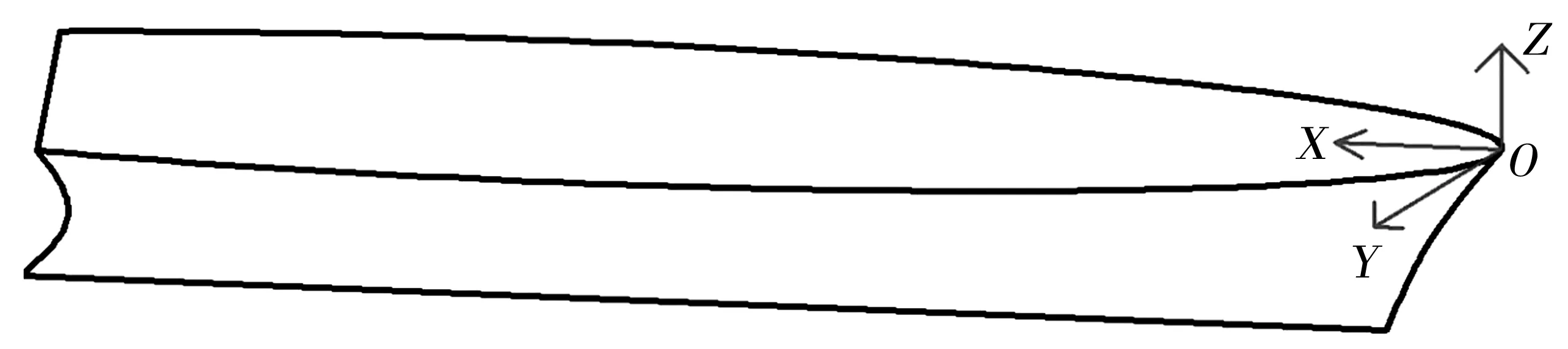
图2 船舶坐标系定义Fig. 2 Definition of coordinate system

船体主要参数如表1。

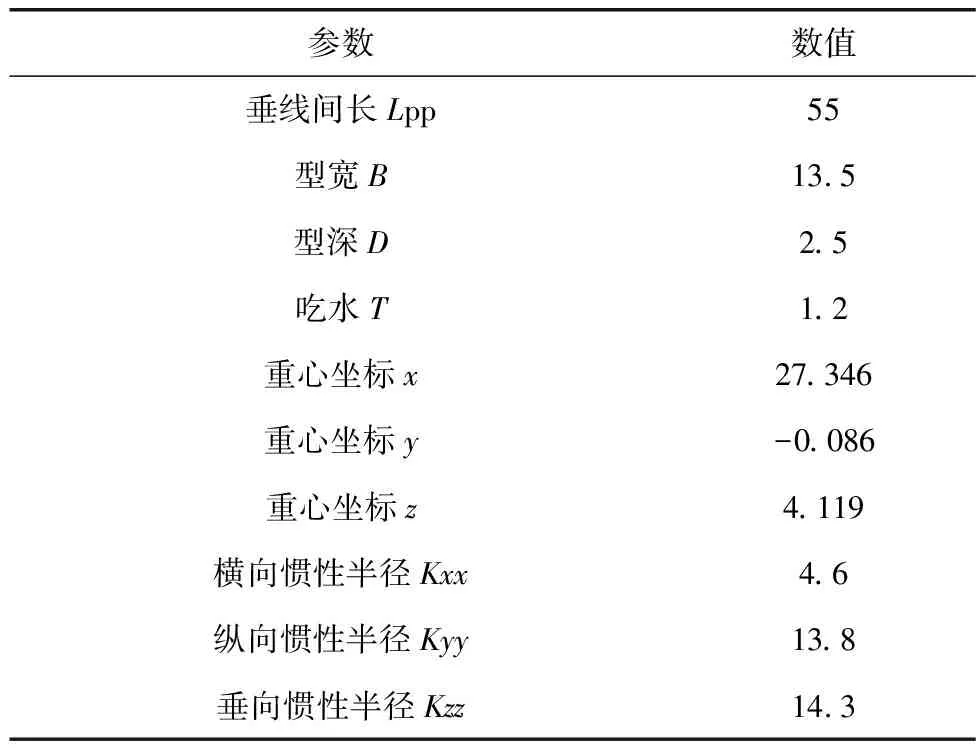
表1 船体主要参数Table 1 Main parameters of hull m

运用 ANSYS 中的 DM 模块建立船舶湿表面有限元模型,定义环境参数,并进行合理的网格划分,网格大小设置为1 m,具体模型如图3。

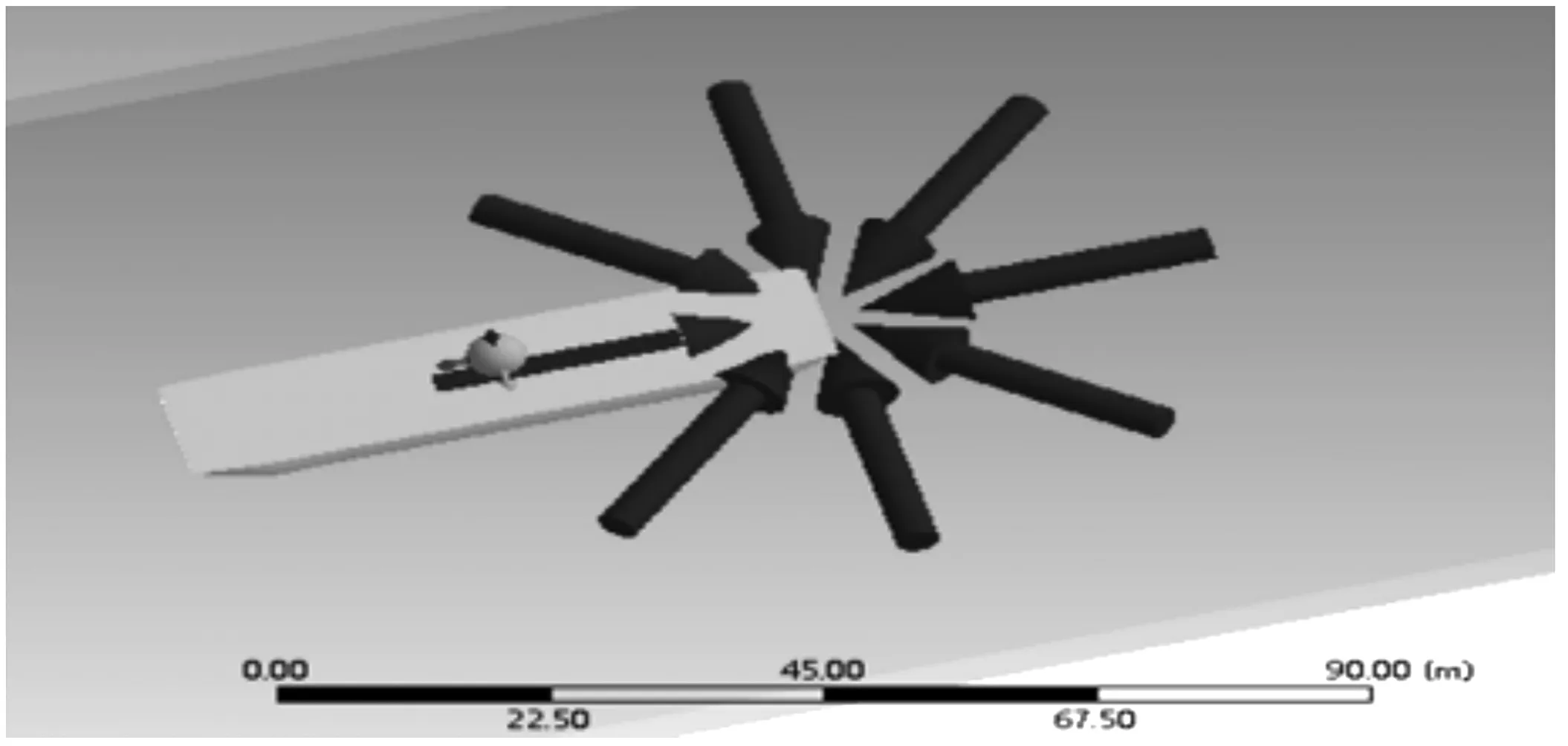
图3 船舶及周边环境模型示意Fig. 3 Schematic diagram of ship and surrounding environment model

2.2 船舶六自由度幅值响应算子

笔者定义频域计算参数如下:船舶工作区域水深5 m;淡水密度1 000 kg/m3;重力加速度9.806 65 m/s2;波浪周期范围-180°～180°,间隔45°;波浪频率0.031 85～0.449 30 Hz。以90°浪向角为例,计算船舶六自由度幅值响应算子,得到其六自由度变化规律,具体如图4～图9。

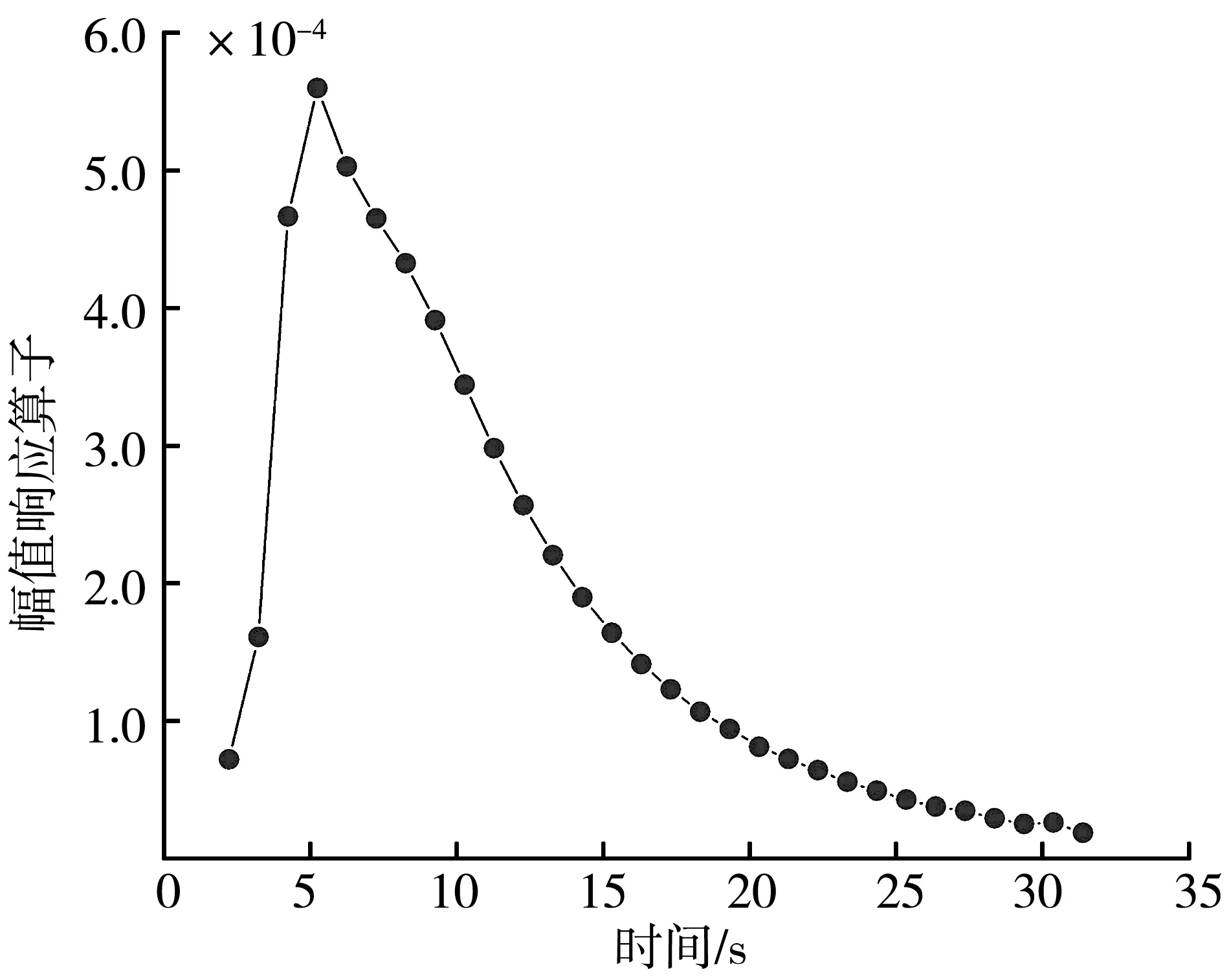
图4 船舶纵荡RAO变化曲线Fig. 4 RAO variation curve of ship surging

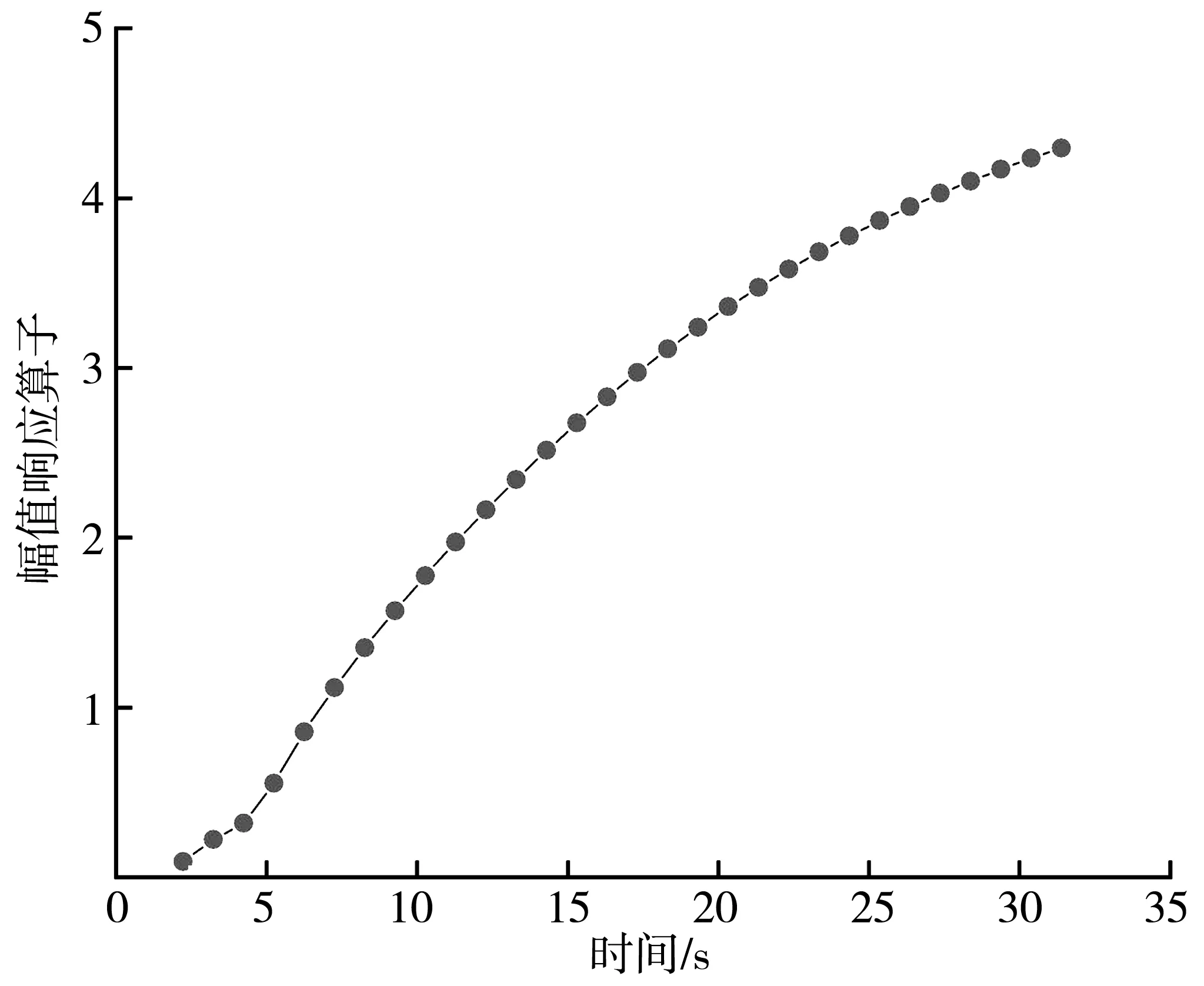
图5 船舶横荡RAO变化曲线Fig. 5 RAO variation curve of ship swaying

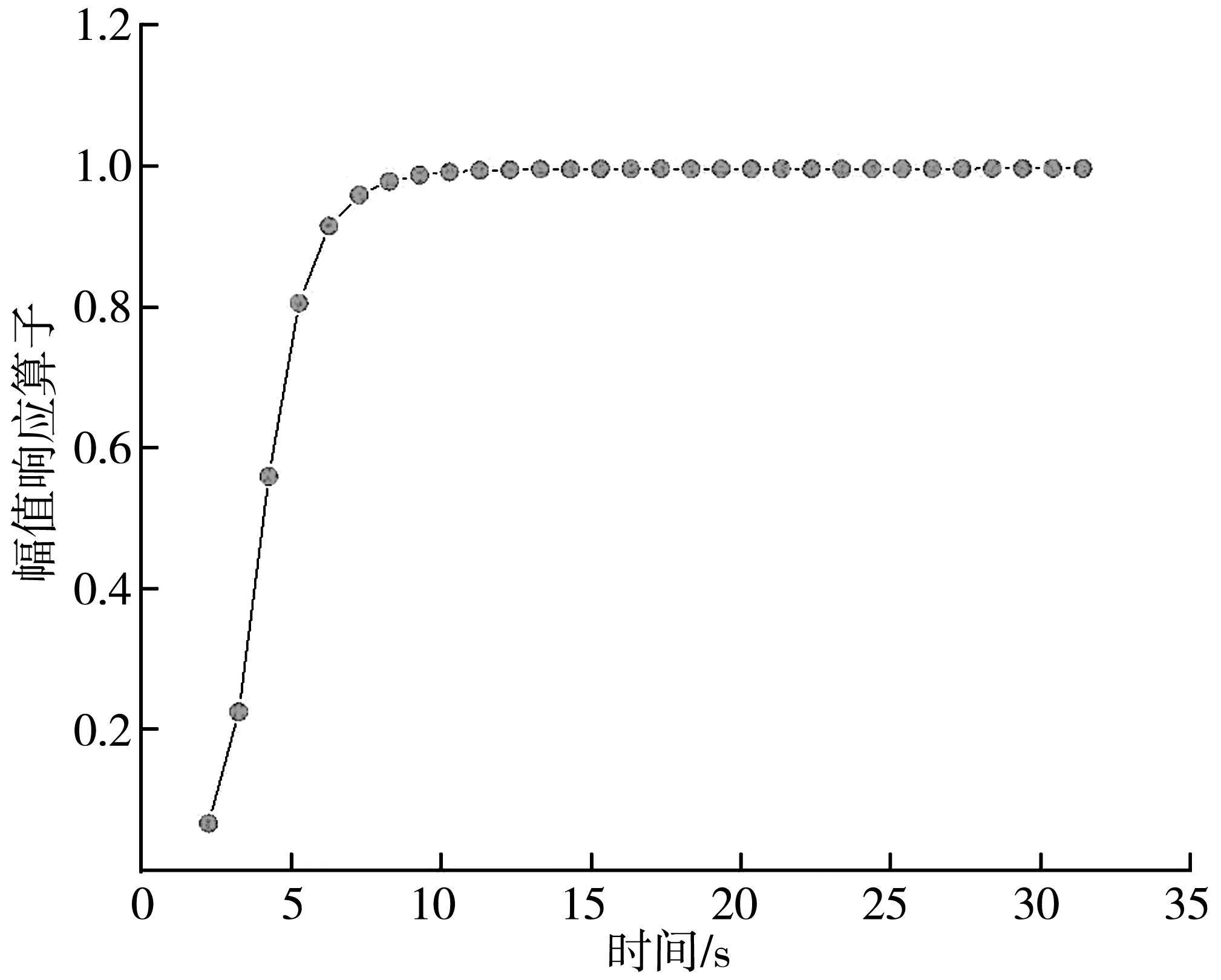
图6 船舶垂荡RAO变化曲线Fig. 6 RAO variation curve of ship heaving

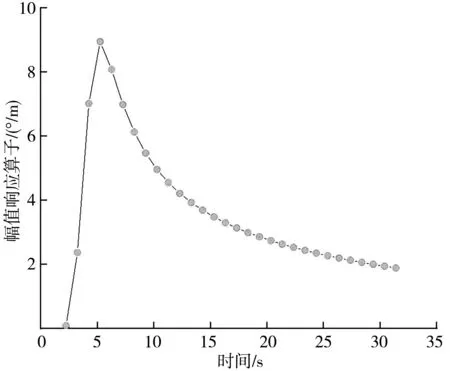
图7 船舶横摇RAO变化曲线Fig. 7 RAO variation curve of ship rolling

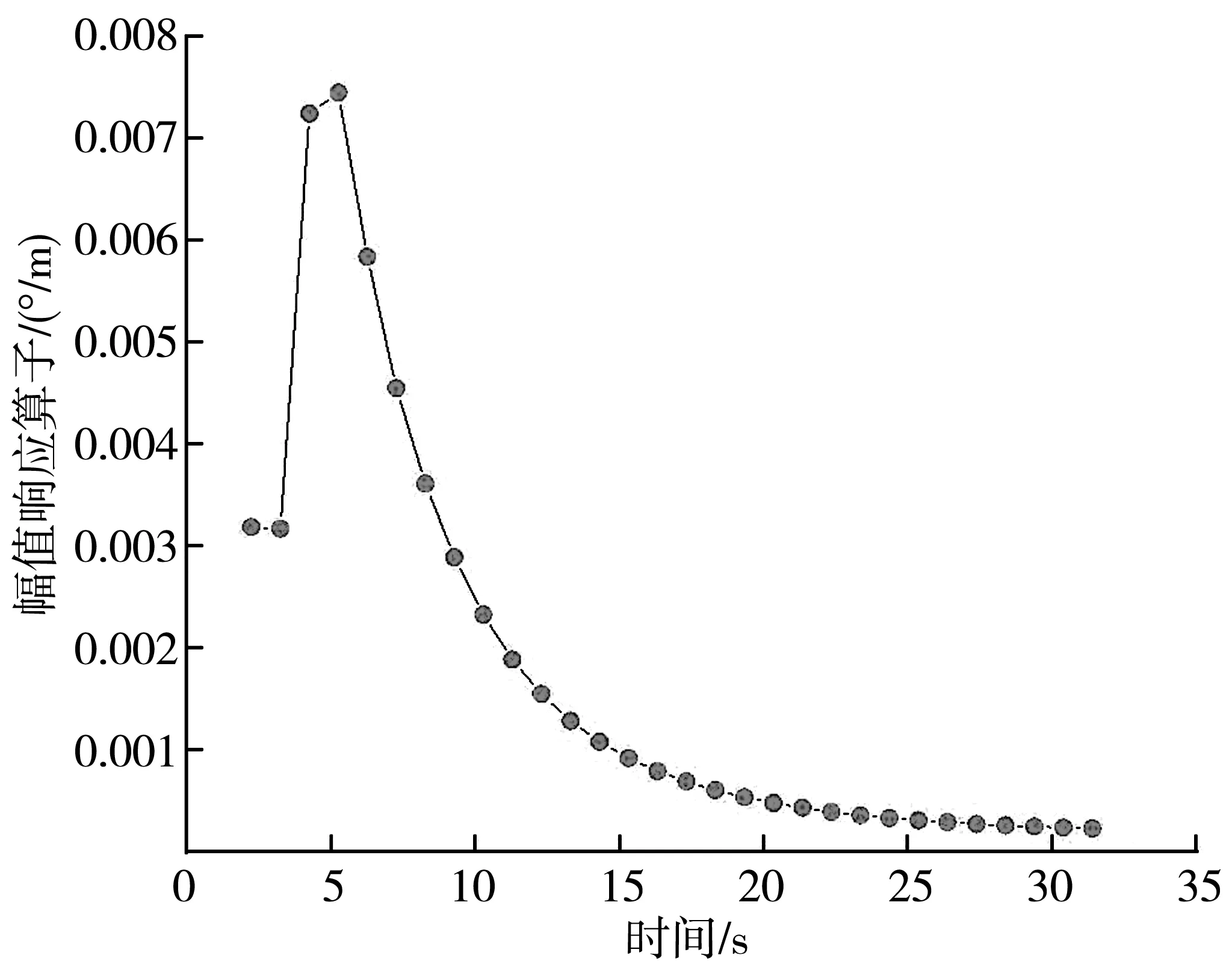
图8 船舶纵摇RAO变化曲线Fig. 8 RAO variation curve of ship pitchcing

由图7和图8分析可得,船舶横摇、纵摇的固有周期是5.08 s和7.09 s。由图4、图7,图8可知,在纵荡、横摇、纵摇运动方向上的变化趋势大体相同,均是在2～6 s的范围内呈上升的趋势,在6 s左右达到最大值后,曲线呈缓慢下降趋势,最后趋于稳定。

由图5、图6,图9可知,在横荡、垂荡、艏摇运动方向上,幅值响应算子曲线则是随着波浪周期增加呈上升的趋势,尤其是横荡与艏摇运动方向上,上升曲线极为陡峭,说明RAO(幅值响应算子)在这两个方向上受波浪周期影响较大。在垂荡运动方向上可以看出曲线在9 s左右几乎达到了峰值,9 s以后曲线几乎不再发生变化,最终稳定在数值1.0左右。

由图4～图9分析可得,在90°浪向角的波浪作用下,平动运动中,横荡的运动响应最为强烈,最大值达到4.29;转动运动中,横摇的运动响应最为强烈,最大值达到8.95。

3 系泊系统计算结果与分析

笔者设定的水域为220 m×100 m,运用ANSYS WORKBENCH中的Hydrodynamic Response模块对目标船舶设计两种不同的系泊缆绳布置方案,并对环境载荷进行相同设置,对系泊状态下的船舶进行时域耦合分析,对得到的船舶运动响应以及系泊缆绳的张力进行分析和比较。

3.1 系泊试验模拟条件

3.1.1 环境条件

结合三峡库区浅水域的实地考察情况和相关资料,为了准确模拟船舶系泊状态下的运动情况和计算缆绳张力,本系泊系统的具体风、浪、流环境条件如表2。

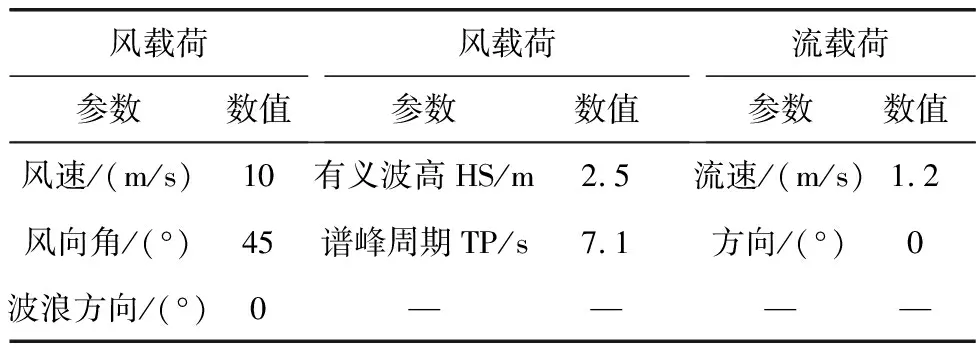
表2 环境条件定义Table 2 Definition of environmental conditions

3.1.2 系泊缆属性

两种系泊系统的设计采用的均为悬链式系泊系统,运用 AQWA 对其进行完全时域耦合分析前,其系泊缆绳在系泊状态下是处于松弛的状态,并留有一定的预张力,具体参数详见表3。

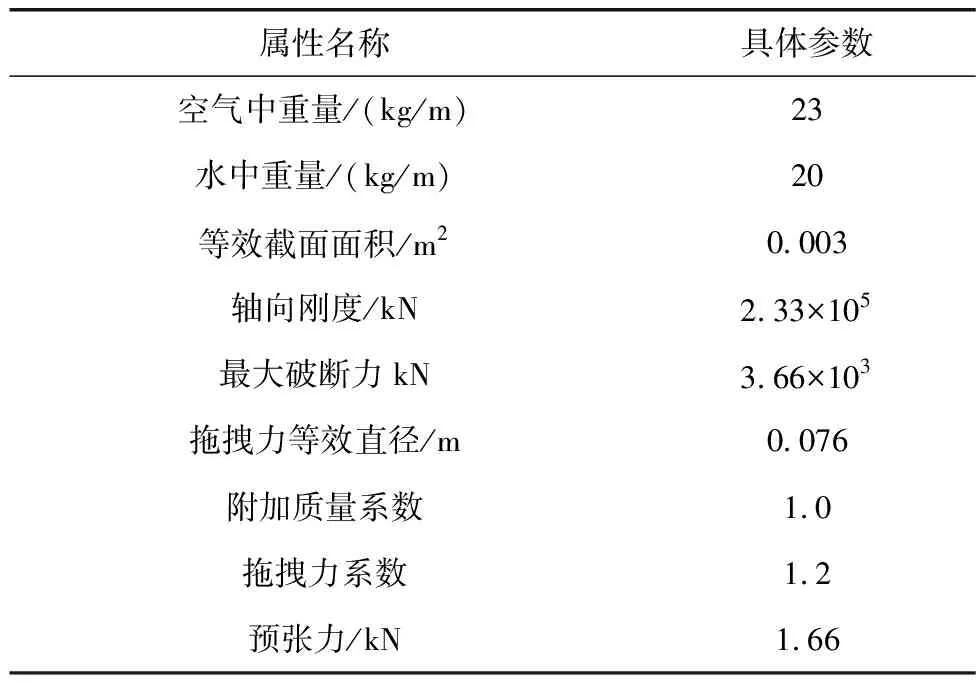
表3 系泊缆属性Table 3 Mooring cable attribute

3.1.3 系泊系统缆绳布置方式

所设计的两种系泊系统,均由8根系泊缆绳组成。图10为4-4的缆绳布置方式,呈对称式分布,在XOY平面内,每个位置的两根缆绳分别于X轴的夹角为30°和60°。

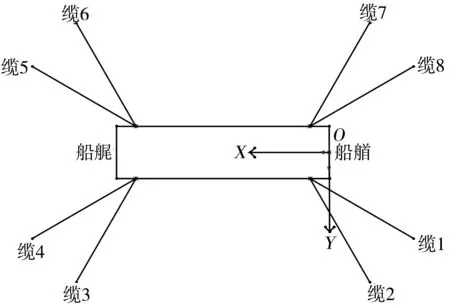
图10 4-4系泊缆绳悬链式布置计算模型Fig. 10 4-4 calculation model of mooring rope catenary arrangement

根据上文给出的坐标系定义,导缆孔与锚点在全局坐标系下的坐标位置如表4。

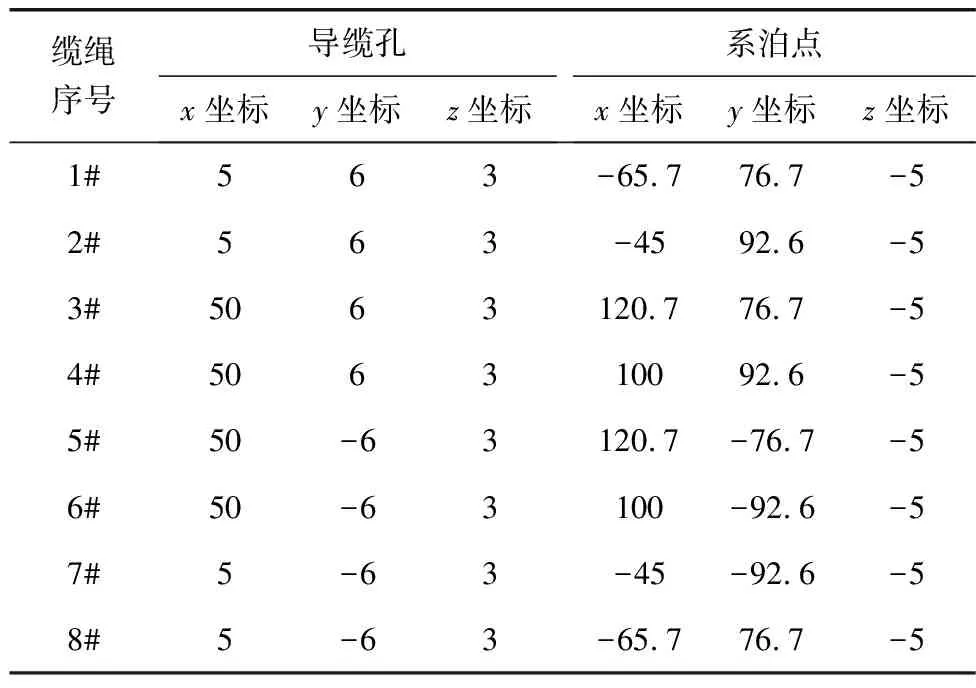
表4 4-4系泊方案缆绳坐标Table 4 4-4 mooring scheme cable coordinates m

图11为4-2-2的缆绳布置方式,在左右两舷各加一根系泊缆,在迎浪方向的船艏处也加上两根对称分布的系泊缆。

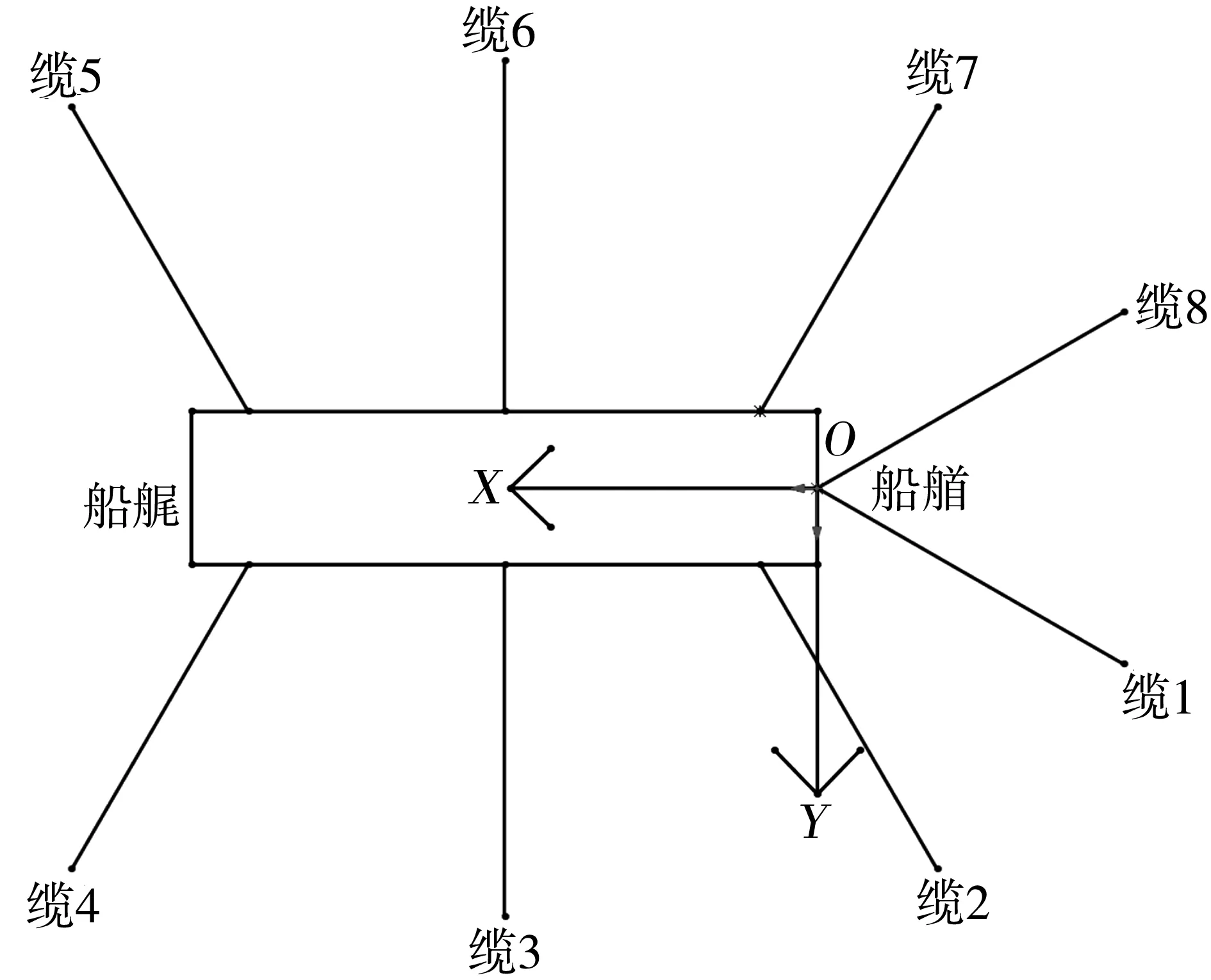
图11 4-2-2系泊缆绳悬链式布置计算模型Fig. 11 4-2-2 calculation model of mooring rope catenary arrangement

导缆孔与锚点在全局坐标系下的坐标位置如表5。

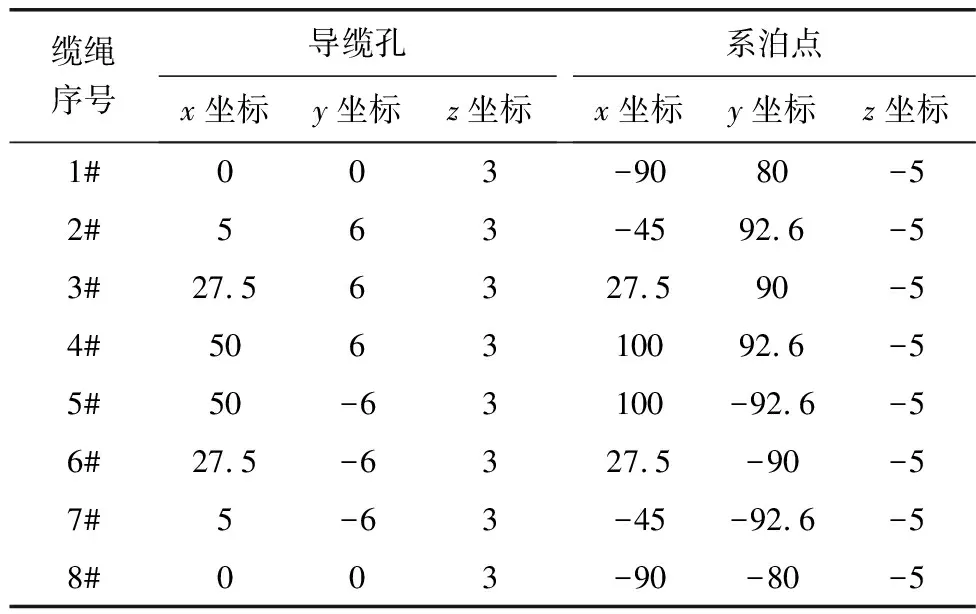
表5 4-2-2系泊方案缆绳坐标Table 5 4-2-2 mooring scheme cable coordinates m

3.2 时域耦合计算结果与分析

3.2.1 船舶运动响应计算结果对比

通过时域分析系泊船舶在水深5 m,浪流方向角0°,风向角45°的环境条件下的运动响应。取时间历程曲线中的3 000～4 000 s时间段作图,其中横荡与艏摇运动幅值较小,几乎可以忽略不计,因此不再进行详细描述。具体如图12～图15。

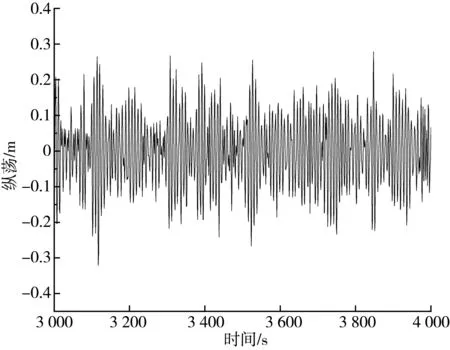
图12 船舶纵荡运动时历曲线Fig. 12 Time history curve of surge for ship

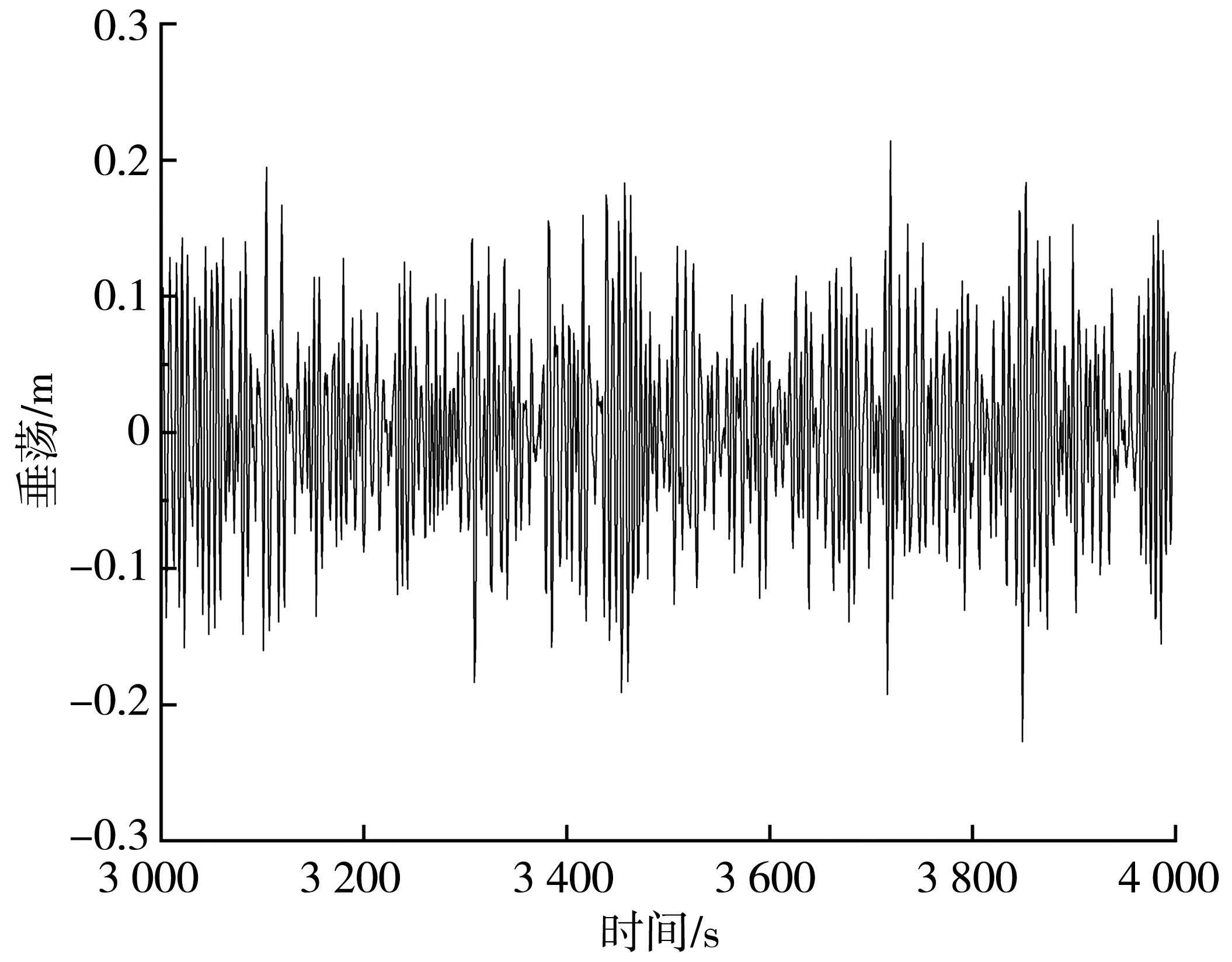
图13 船舶垂荡运动时历曲线Fig. 13 Time history curve of heave for ship

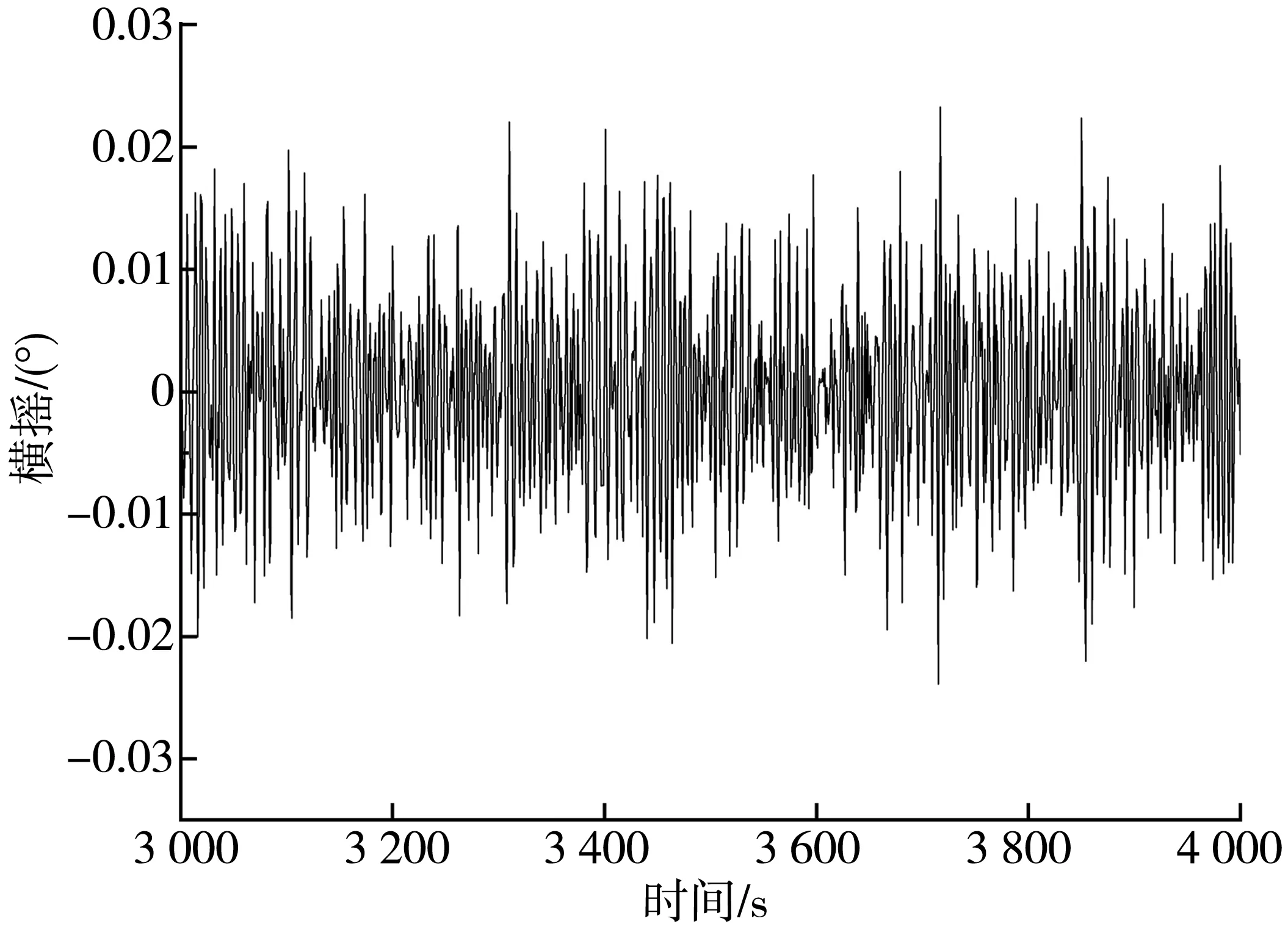
图14 船舶横摇运动时历曲线Fig. 14 Time history curve of roll for ship

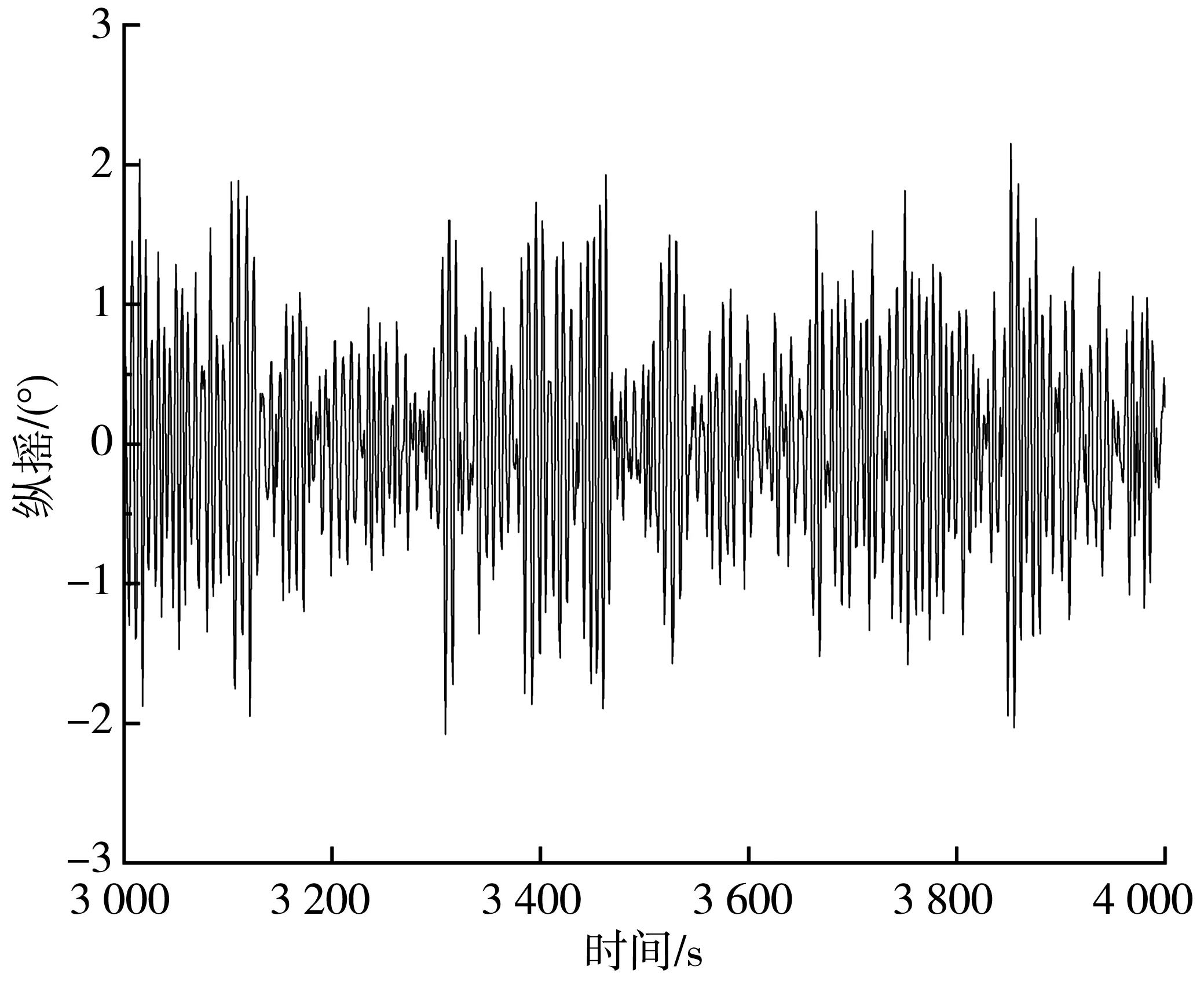
图15 船舶纵摇运动时历曲线Fig. 15 Time history curve of pitch for ship

结合图12～图15以及时域分析的计算结果可以得到,在给定的环境条件下船舶运动响应结果,如表6。运动范围为船舶各个自由度运动最大值与最小值绝对值相加。

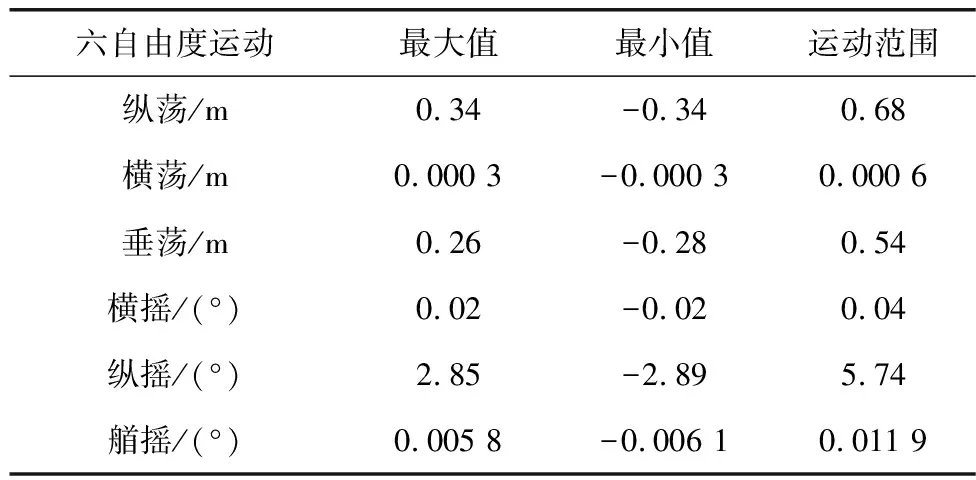
表6 船舶运动响应计算结果Table 6 Calculation results of ship motion response

通过对图12～图15以及表6分析可得,由于环境载荷的不规则造成了船舶六自由度呈现出不规则的变化趋势。当浪流方向角为0°,风向角45°时,船舶系泊状态下的平动运动中,纵荡运动响应最为剧烈,多数时间内其运动响应值小于0.3 m,运动幅值最大,达到了0.34 m,相当于水深的6.8%;然而横荡运动幅值最小,几乎可以忽略不计;垂荡运动响应值多数时间内小于0.2 m,运动幅值为0.28 m;在转动运动中,纵摇运动较横摇,艏摇更加强烈,多数时间内其运动响应值小于2°,运动幅值最大,达到2.89°;艏摇运动幅值最小,只有0.01°;横摇运动响应值多数时间内小于0.02°,运动幅值为0.02°。从结果上看,两种缆绳布置方案将船舶整体运动响应约束在一个较小的范围内。

3.2.2 系泊缆张力计算结果与对比分析

虽然系泊缆是对称布置的,但在浪流方向角为0°,风向角为45°的情况下,每根系泊缆的张力会有所不同,选取最接近风浪流作用位置的两根系泊缆绳,1号缆绳和8号缆绳作为时域耦合分析对象。两种缆绳布置方案下的缆绳张力时间历程曲线图,如图16～图19。

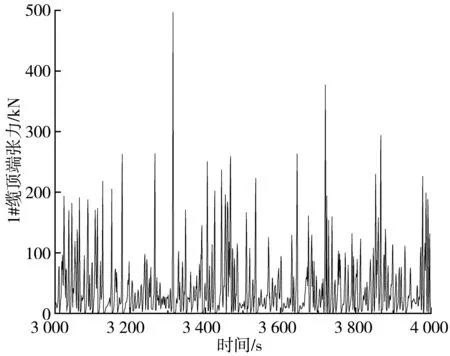
图16 4-4系泊方案中1#系泊缆顶端张力时历曲线Fig. 16 Time history of tension at the top of 1# mooring cable in 4-4 mooring scheme

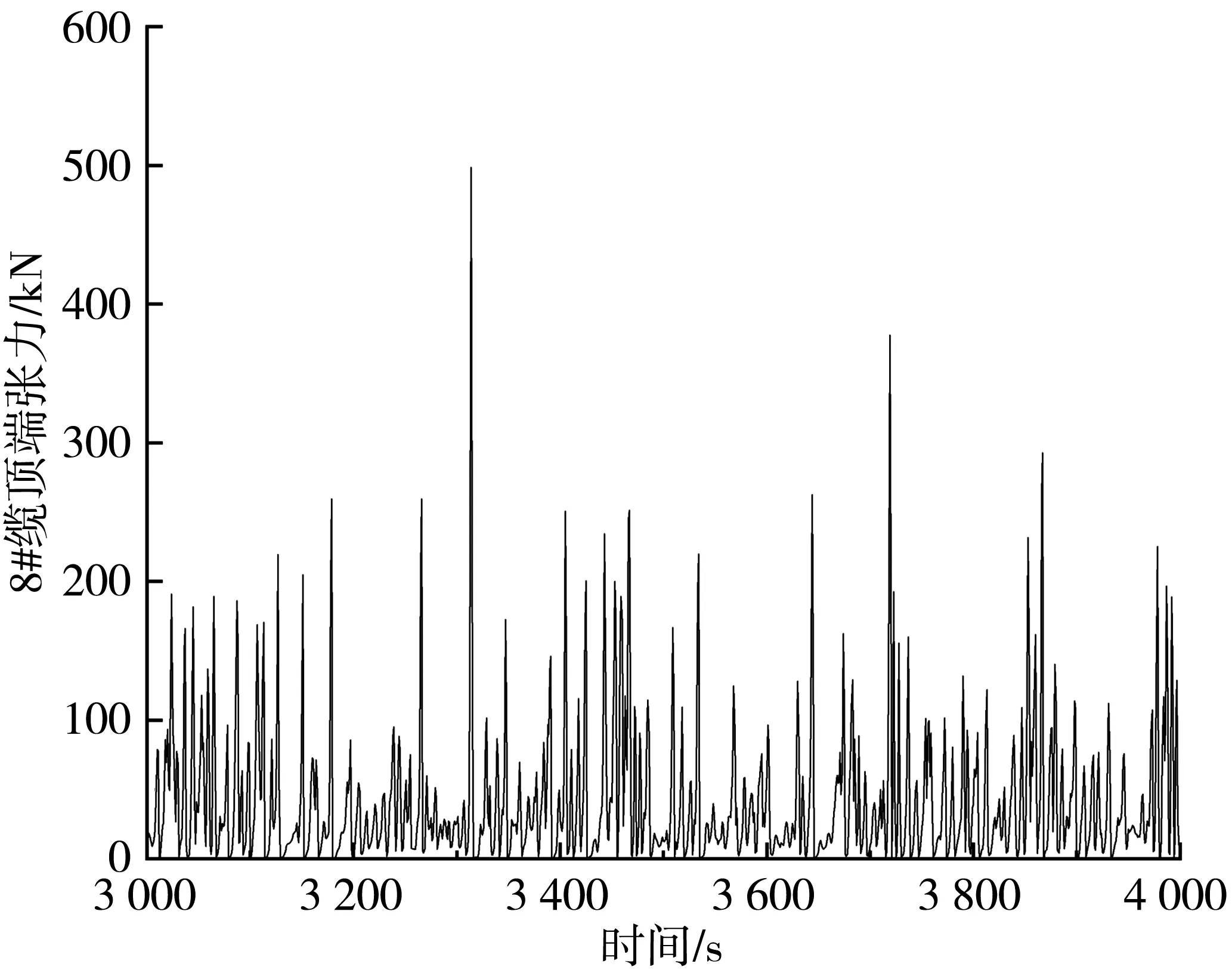
图17 4-4系泊方案中8#系泊缆顶端张力时历曲线Fig. 17 Time history curve of tension at the top of 8# mooring cable in 4-4 mooring scheme

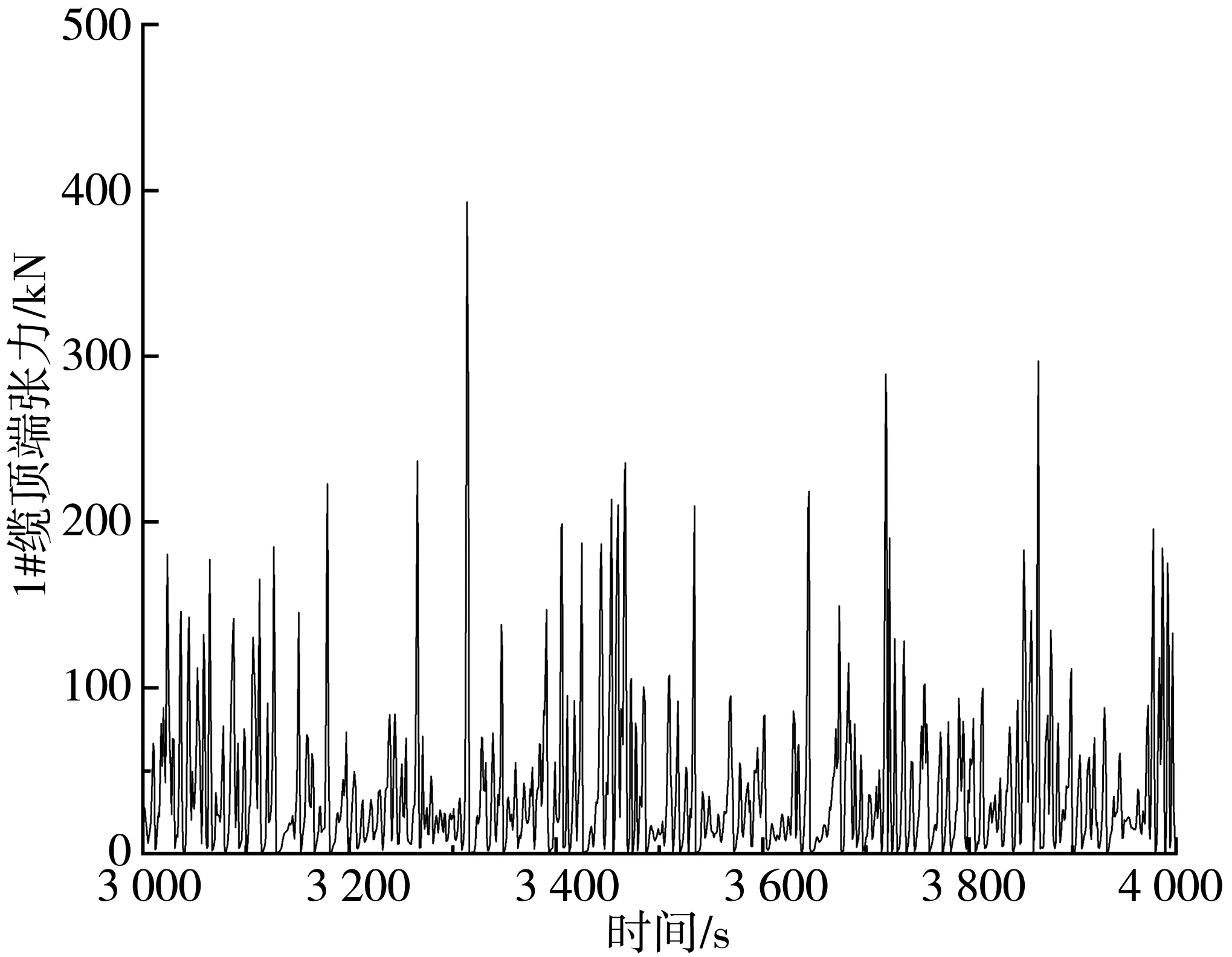
图18 4-2-2系泊方案中1#系泊缆顶端张力时历曲线Fig. 18 Time history curve of tension at the top of 1# mooring cable in 4-2-2 mooring scheme

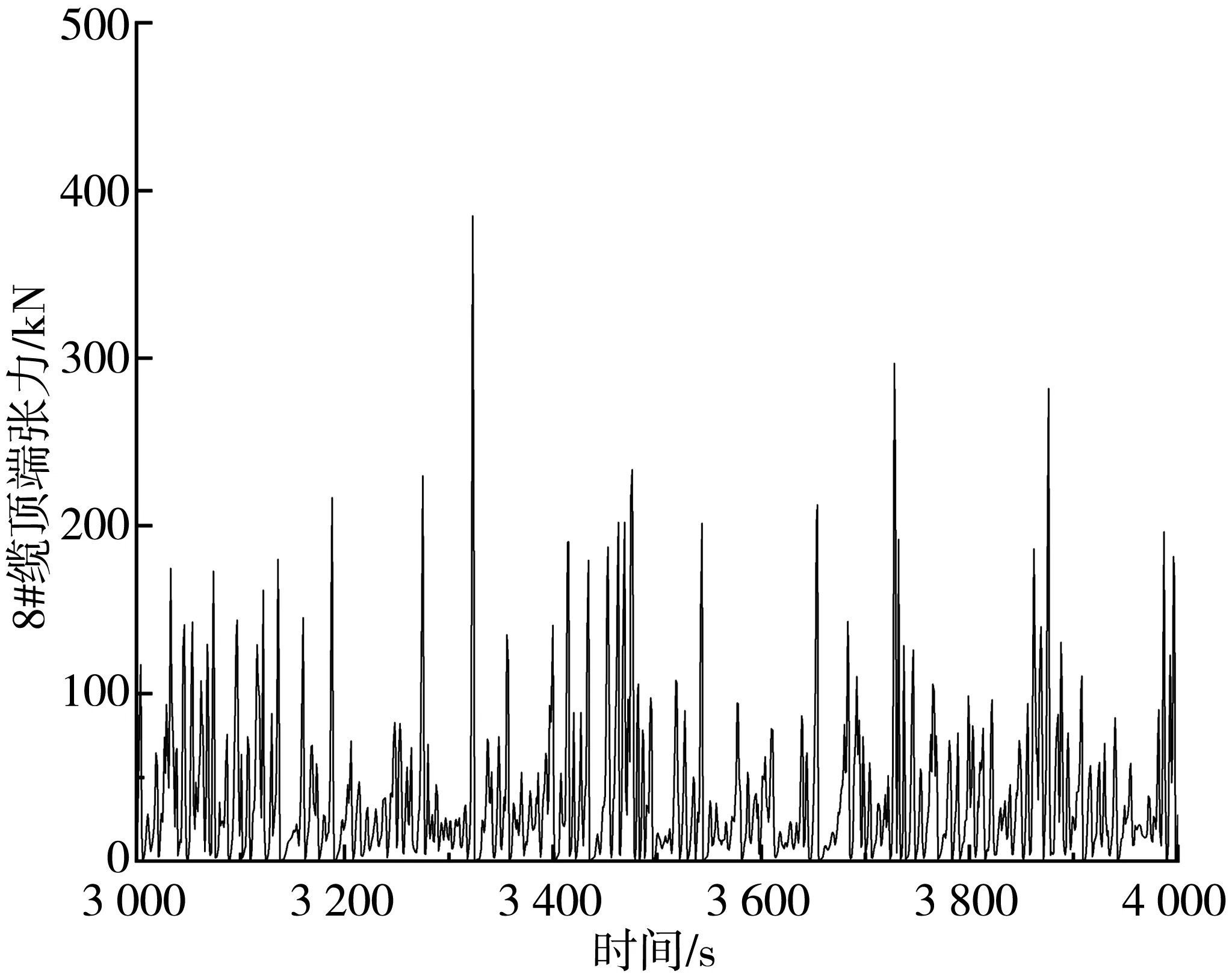
图19 4-2-2系泊方案中8#系泊缆顶端张力时历曲线Fig. 19 Time history curve of tension at the top of 8# mooring cable in 4-2-2 mooring scheme

结合图16～图19以及完整的计算结果可得,在风浪流作用下8根系泊缆的张力变化及其数值的大小,系泊缆张力具体计算结果如表7。

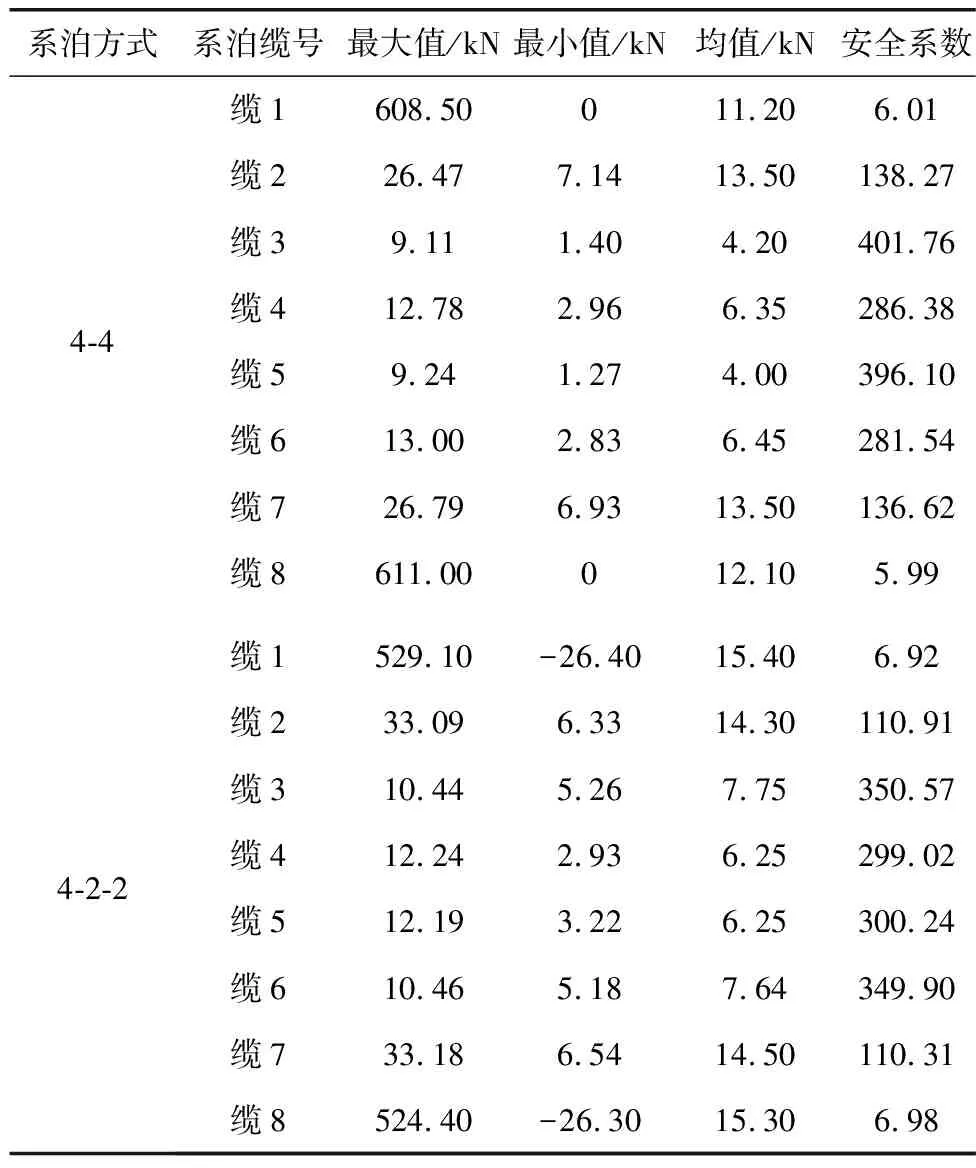
表7 系泊缆张力计算结果Table 7 Calculation results of mooring cable tension

结合图16～图19以及表7可知,在浪流方向角为0°、风向角为45°时,8根系泊缆受环境载荷作用张力呈周期性变化。在环境载荷施加时,船艏处最靠近风浪流作用位置的缆1和缆8最先受到载荷的作用,受到的张力远远大于其他缆绳所受到的张力,4-4缆绳布置方式下最大拉力出现在缆8,最大值为611 kN;4-2-2缆绳布置方式下最大拉力出现在缆1,最大值为529.1 kN,其余缆绳的张力相对而言较小,可不用考虑缆绳断裂问题。根据有关规范,当系泊系统处于完整状态时,若采用动力法进行评估,系泊缆张力的安全系数至少为1.67,才能保证系泊船舶的安全性。在文中系泊缆的两种布置中,缆1的安全系数分别为6.01,6.92;缆8的安全系数分别为5.99,6.98,均有相当的安全裕度,满足有关规范的要求,设计合理。

同时,在同样的环境条件下,4-2-2缆绳布置方案中系泊缆安全系数相对而言比4-4缆绳布置方案中的更为均衡,即各缆绳受力较之前更加均衡。在安全系数富裕的情况下,4-2-2缆绳布置方案更能保证系泊船舶的安全。两种系泊系统的时域响应结果对比,也可以为今后船舶应急系泊提供思路,当浪流方向角为0°时,可以通过增加船艏处的系泊缆数量来提高系泊系统抵御环境载荷的能力,保证系泊状态下船舶的安全性。

4 结 论

基于三维势流理论,以三峡库区浅水域船舶为分析对象,采用 ANSYS-AQWA 软件,进行频域分析以及系泊状态下的时域耦合分析。在频域分析下得到船舶六自由度的相关水动力参数及其变化规律。在环境参数不变,缆绳数量一定的前提条件下,改变其布置方式,优化设计两种不同的系泊系统方案,时域耦合分析系泊状态下船舶运动响应以及系泊缆张力,主要结论如下:

1)在90°浪向角下,船舶六自由度运动响应幅值算子随波浪周期的变化各有不同。在纵荡、横摇以及纵摇运动方向上,呈先增大后减小的趋势;而在横荡、垂荡、艏摇运动方向上,曲线则是随着波浪周期增加一直呈上升的趋势,尤其是横荡与艏摇运动方向上,上升曲线极为陡峭,说明 RAO(幅值响应算子) 在这两个方向上受波浪周期影响很大。

2)在同样的环境条件下,4-2-2缆绳布置方案中缆1和缆8的缆绳最大张力较4-4缆绳布置方案也有所改善,缆1最大张力降低13%,缆8最大张力降低14%;同时4-2-2缆绳布置方案中的缆绳受力更为均衡,也就更能保证系泊船舶的安全,且缆绳安全系数裕度较大。4-2-2缆绳布置方案较4-4缆绳布置方案有更加明显的合理性,优越性。