基于联合静动力修正模型的斜拉桥换索方案

齐东春,王宇飞,李 琦,赵志国

(1. 国家山区公路工程技术研究中心,重庆 400067; 2. 防灾减灾湖北省重点实验室(三峡大学),湖北 宜昌 443002; 3. 三峡大学 土木与建筑学院,湖北 宜昌 443002)

0 引 言

斜拉索是斜拉桥重要的受力构件,被视为斜拉桥的生命线。斜拉索在服役过程中产生的主要病害包括拉索护套损伤、钢丝腐蚀及断丝、锚固系统锈蚀等,这使得具有高应力的拉索极容易发生疲劳破坏[1]。国内外普遍认为斜拉索的使用寿命约为20 a,为防止断索事故发生,越来越多的斜拉桥采取定期换索的方式来保证桥梁安全,因此斜拉索更换是斜拉桥服役期间必然面临的问题。1962年建成的第一座现代混凝土斜拉桥——委内瑞拉马拉开波桥,于1978—1981年间对全桥的384根拉索进行了更换,这是国外最早、最具有代表性的斜拉桥换索案例[2]。目前,国内已有50余座斜拉桥因各种原因更换了拉索;基于斜拉桥大规模建成的年代、拉索使用寿命等因素,预计需要更换拉索的斜拉桥数量将在不久的将来出现爆发式增长。

斜拉索的索体主要有两种形式:平行钢丝和平行钢绞线;我国90%以上的斜拉桥均采用平行钢丝的拉索。从斜拉索安装及更换角度来看,平行钢绞线具有可单根张拉、单根更换及检测的优势,能在不中断交通的情况下进行换索,因此部分斜拉桥在更换拉索时会将平行钢丝拉索改为平行钢绞线拉索,如铜陵长江公路大桥[3]。平行钢丝拉索的构造决定了只能通过整根拉索一次更换到位(平行钢绞线拉索可采用单根钢绞线更换,风险较小)。相比于平行钢绞线拉索,平行钢丝拉索更换时的主梁应力变化更为剧烈,研究表明:大索距低梁高的平行钢丝拉索混凝土斜拉桥在换索过程中,主梁正应力变化幅度较大(如铜陵长江大桥换索时应力变化量为8 MPa,而该桥成桥时的压应力储备不足8 MPa),换索过程中主梁可能会出现较大的拉应力而引起梁体开裂[3]。由此可见:主梁正应力超限是大跨度混凝土斜拉桥在确定换索方案时的主要制约因素。

混凝土斜拉桥在服役期受混凝土徐变、预应力损失、斜拉索锈蚀及松弛效应、梁体开裂引起刚度变化等因素影响,会导致结构的实际状态与设计状态偏差变大。对主要计算参数进行修正以明确换索前的初态,是确定换索方案的前提条件[4]。由于换索时一般会只对换索索号附近区域有一定影响,因此可先分析拆除单根拉索时对剩余结构影响,对换索方案进行大致预判,然后再结合施工效率拟定详细的换索方案,包括每次换索数量、换索方式(对称换索或非对称换索),最后获得合理的换索方案[5-8]。

笔者以某主跨450 m的平行钢丝混凝土斜拉桥(PC斜拉桥)为背景,采用联合静动力法对有限元模型进行修正,使有限元模型与结构实际情况更为吻合,再对不同位置拉索的结构敏感性进行分析,对不同换索方案进行分析比较,确定较为合理的换索方案。

1 换索前有限元计算模型

1.1 工程背景

该桥为双塔双索面全飘浮体系混凝土斜拉桥,跨径组合为(198+450+198)m。主梁采用双主肋截面,梁高2.7 m,梁宽30.6 m,肋宽1.8 m;斜拉索采用φ7平行钢丝索,全桥共计220根;主梁上拉索间距为8.1 m,梁高与索距之比为1/3,梁高与跨径之比为1/167;半跨立面如图1,主梁标准横断面如图2。该桥于2001年12月建成,至今已运营了20 a。

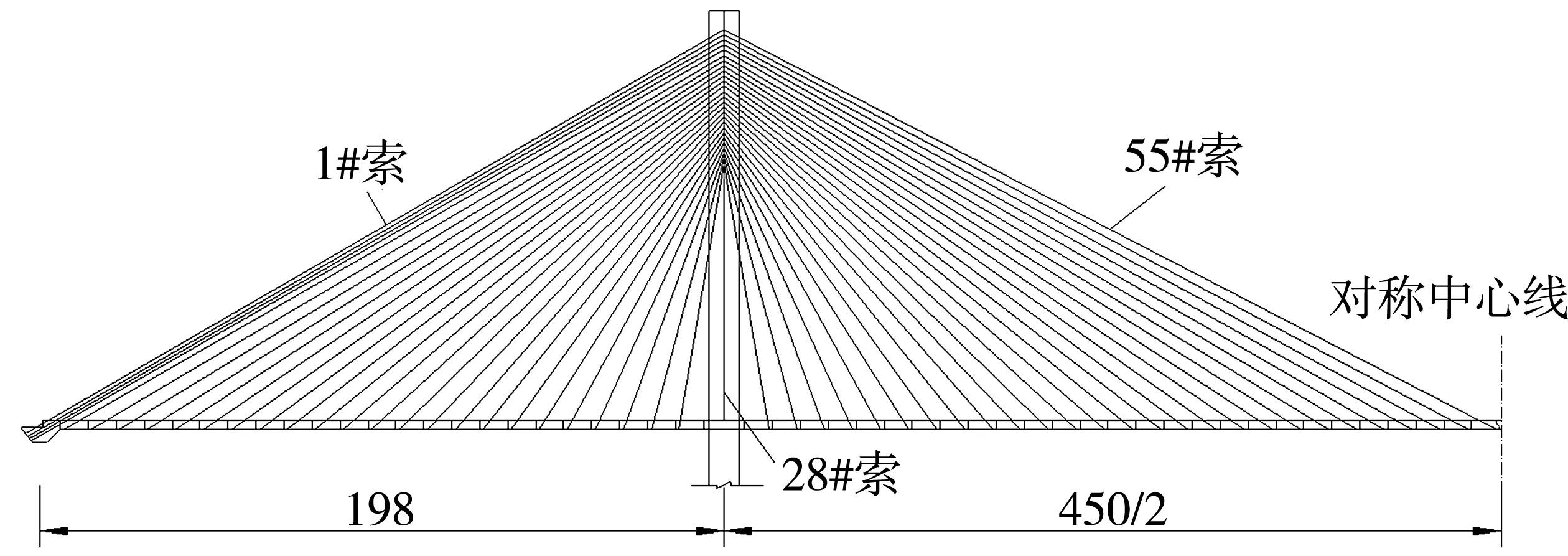
图1 半跨立面(单位:m)Fig. 1 Half-span elevation

图2 主梁标准横断面(单位:cm)Fig. 2 Standard cross section of main beam

1.2 有限元模型

有限元计算模型如图3,主梁及索塔采用空间梁单元,斜拉索采用索单元。在索塔处,主梁节点仅约束侧向自由度;在边墩处,主梁节点仅约束竖向自由度,墩底固结。

图3 有限元计算模型Fig. 3 Finite element calculation model

按照实际施工方案,笔者建立了分阶段有限元计算模型,按照成桥状态实测的索力及施工阶段索力和主梁预拱度调整结果,使模型的成桥状态索力及桥面标高与实测结果一致。根据该桥服役若干年后的静动载试验数据,选择合适的方法对有限元模型进行修正,使模型与该桥的实际状态相吻合,并在此基础上进行换索方案分析。

在建立有限元模型时,为反映出主梁受力的空间效应,采用梁格法将主梁截面划分为双主梁模型,以便克服单主梁模型中主梁正应力的误差。将主梁沿中线纵向划分为双主梁,双主梁通过横梁联系,横梁由横隔板及两侧顶板组成,为T形截面。主梁的梁肋、桥面板及桥面系质量均分配给主梁单元,横格板质量分配给横梁单元。主梁及横梁均考虑剪力滞效应,对顶板宽度进行折减。由于横梁为变截面,需分别计算每段横梁的惯性矩,为简化计算,采用等效横梁代替变截面横梁,如图4。等效原则为:在相同竖向弯矩或扭矩作用下,悬臂端的竖向转角或扭转角相等。在计算横梁的抗扭惯性矩时,顶板按“板”计算,横隔板按“梁”计算[9]。横隔板及主梁惯性矩计算结果见表1。

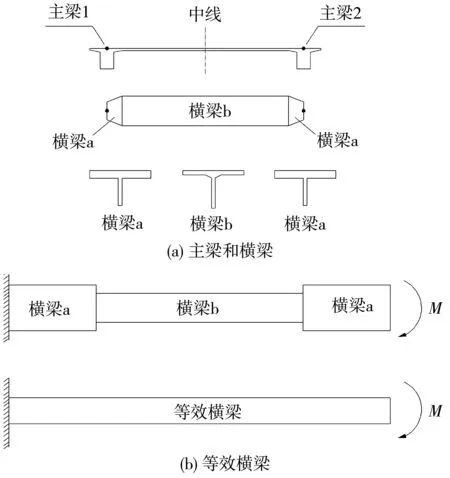
图4 主梁、横梁及等效横梁示意Fig. 4 Schematic diagram of main beam, cross beam, and equivalent beam

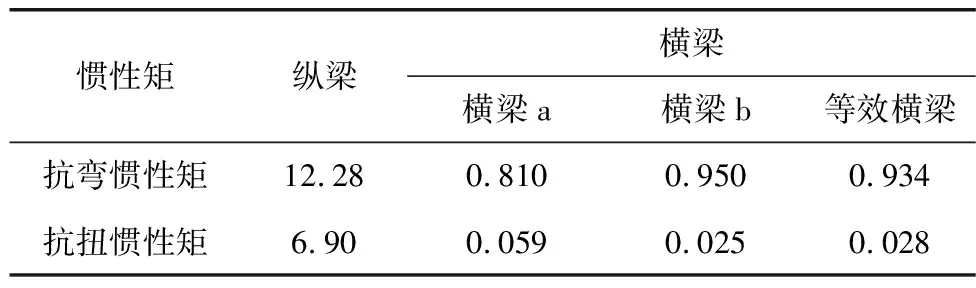
表1 梁格惯性矩计算结果Table 1 Inertial moment calculated by grillage method m4

1.3 有限元模型修正

采用联合静动力的有限元模型修正方法,构造双目标优化函数;基于NSGA-Ⅱ算法求解得到Pareto最优解集[10-11];利用最大弯曲角法,从Pareto最优解集中寻找协调最优解;实现了有限元模型的修正[12-13]。根据该桥实际情况,选择塔梁弹性模量、主梁容重、主梁刚度、支座刚度等参数进行灵敏度分析,对参数施加微小扰动,根据结构响应值变化情况计算参数灵敏度[4,12],灵敏度分析结果见图5。根据图5选择灵敏度较大的主梁、索塔和主墩弹性模量及主梁抗弯惯性矩作为模型修正参数,其中弹性模量修正范围控制为-10%～30%,主梁抗弯惯性矩修正范围控制在-10%～5%[12,14]。

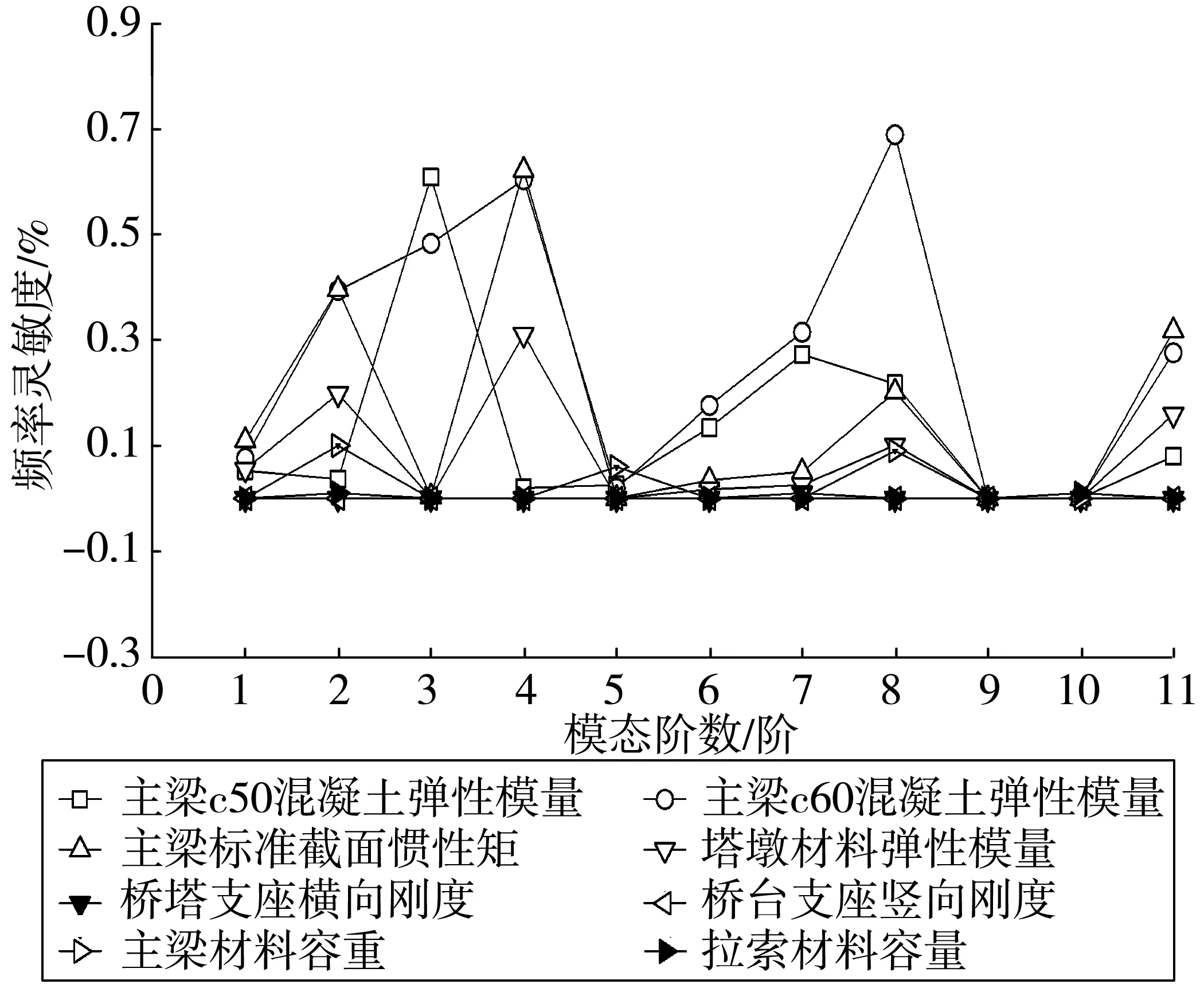
图5 参数频率灵敏度分析结果Fig. 5 Frequency sensitivity analysis results of parameters

静力荷载作用下的结构位移测量相比于应力测量更为方便且精度更高,而自振频率对结构刚度的变化较为敏感,因此可采用位移和频率实测结果与理论计算结果来构造目标函数。笔者选择车道荷载作用下的主梁跨中最大正弯矩值进行加载试验。在该工况下,主梁边、中跨位移均较大,测试误差相对较小,因此模型修正效果较好;同时选择主梁前7阶自振频率作为动力实测数据来源。联合静动力有限元模型修正目标函数可由式(1)表示。

min{F1,F2}=

(1)

式中:Uaji、Utji分别为第j工况下i点处的有限元模型静力位移理论计算值和实测值;γj为第j工况下的权重系数;fai、fti分别为结构自振频率理论计算值和实测值;n为自振频率阶数。

1.4 检测工况与有限元模型修正

主梁跨中最大正弯矩工况静力位移测点布置如图6,模态实验测点布置如图7。每个测点均布置竖向、横向及纵向加速度传感器,利用风荷载、地脉动等环境激励进行模态实验;获得实测静力响应位移、应变及实测动力特性频率、振型等参数。需要注意的是,有限元模型计算振型阶次与实测振型阶次并不一定完全吻合,此时可采用模态判定准则(MAC)进行振型配对[15]。

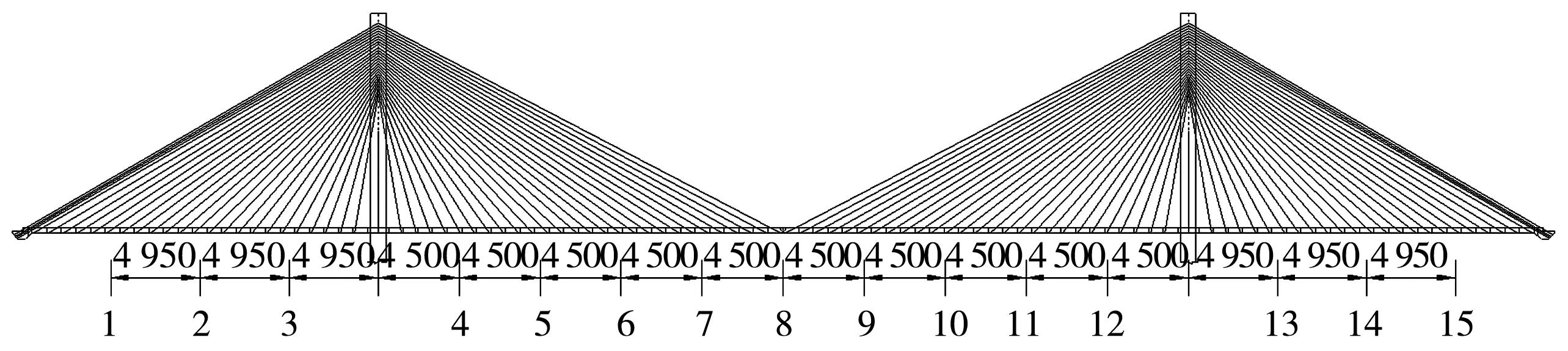
图6 静力位移测点布置(单位:cm)Fig. 6 Layout of static displacement measuring points

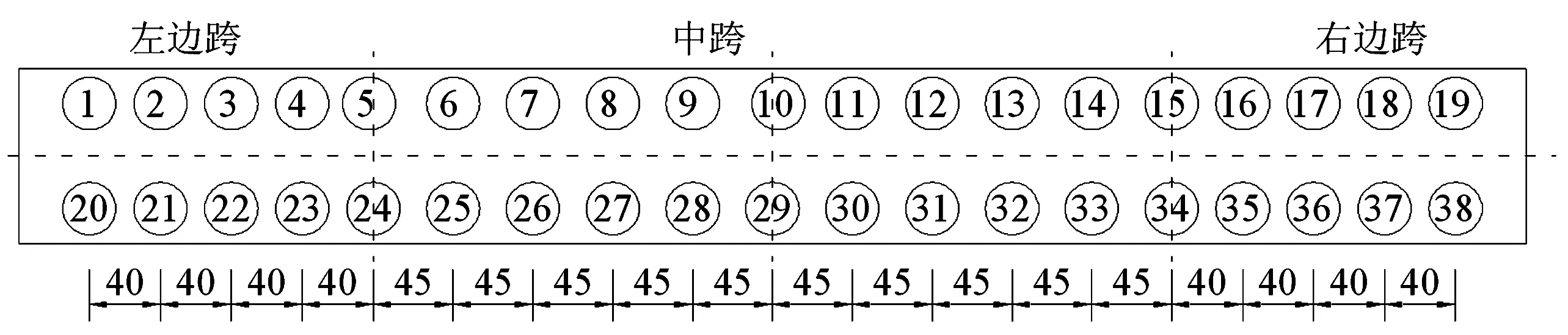
图7 模态实验测点布置(单位:cm)Fig. 7 Layout of measuring points for modal test

NSGA-Ⅱ算法参数为:初始种群大小为100,最大迭代次数为100,交叉概率为0.8,变异概率为0.2。基于静动力的有限元模型修正流程如图8。

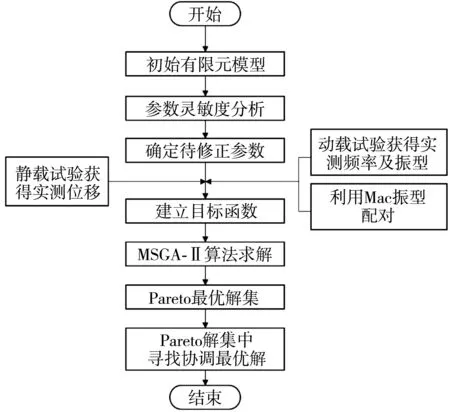
图8 模型修正流程Fig. 8 Schematic diagram of the model modification process

得到该问题的Pareto最优解集如图9。利用最大弯曲角法在Pareto最优解集中找到协调最优解,从而实现了有限元模型的修正。

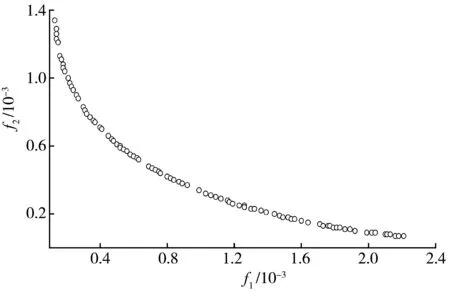
图9 Pareto最优解Fig. 9 Pareto optimal solution

模型参数修正前后对比如表2;模型修正前后静力位移与实测位移对比见表3;模型修正前后自振频率与实测自振频率对比见表4。

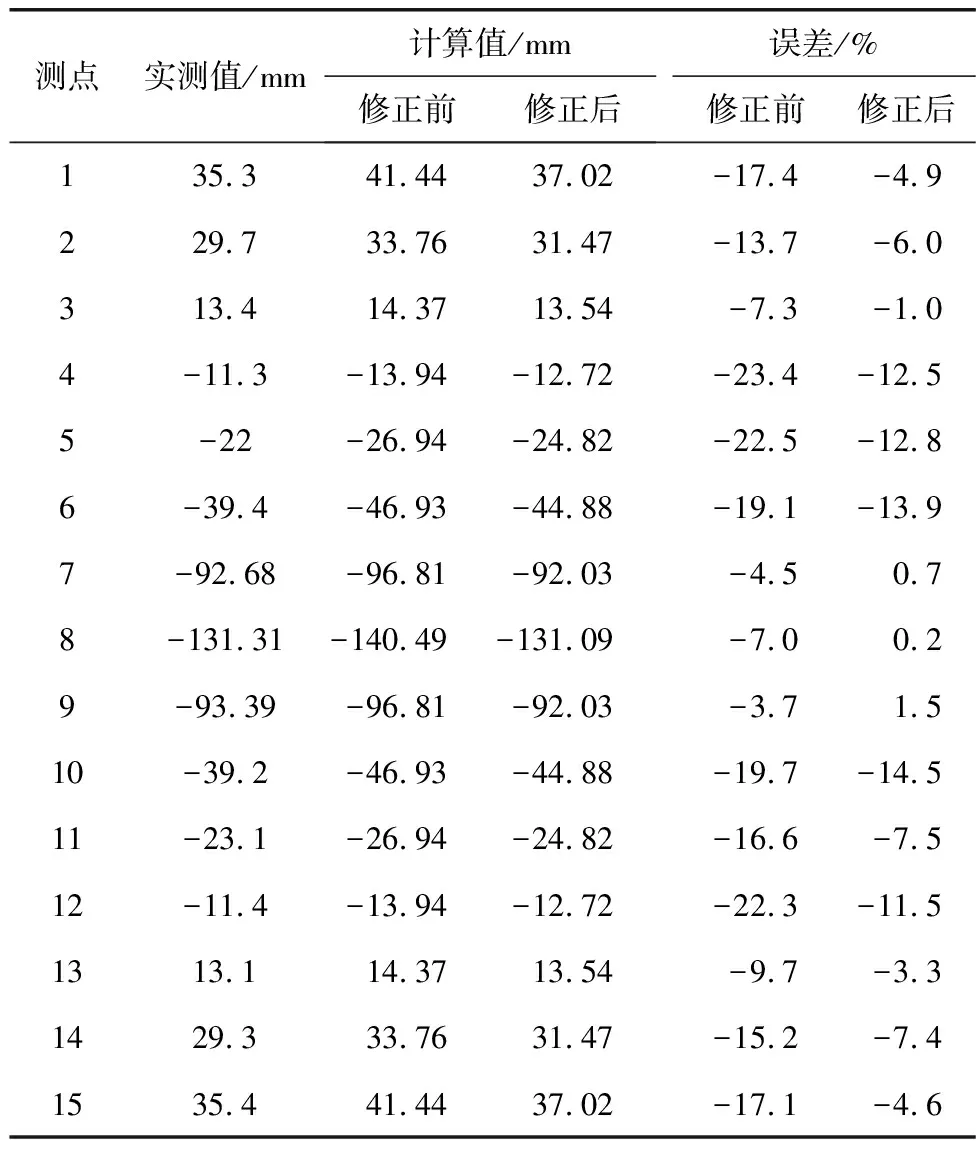
表3 修正前后主梁位移计算值与实测值对比Table 3 Comparison of calculated and measured values of displacement of main beam before and after modification

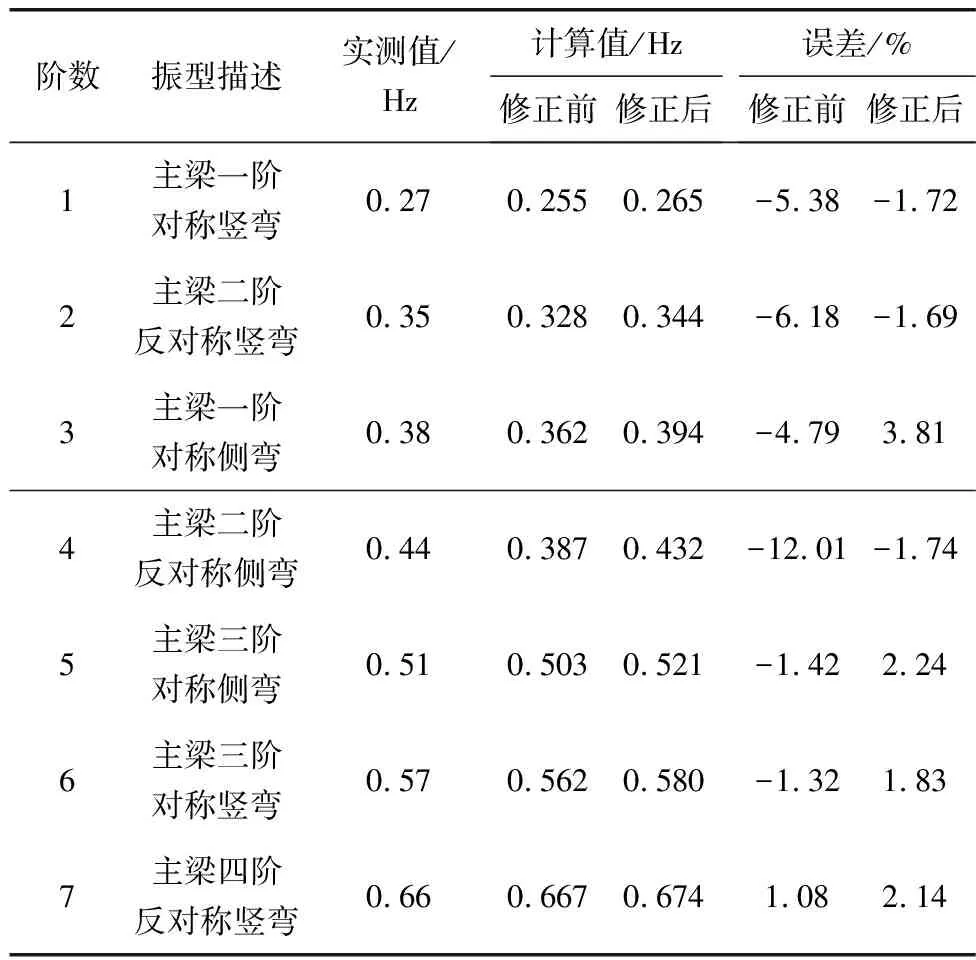
表4 修正前后自振频率计算值与实测值对比Table 4 Comparison between calculated and measured values of natural frequency before and after modification

由表3可知:模型修正后,C60钢筋混凝土主梁弹性模量增大25.8%,钢筋混凝土索塔弹性模量增大24.9%,主梁抗弯惯性矩减小2%,这与文献[12,14]的结论基本吻合。混凝土主梁和索塔的弹性模量修正幅度较大,可能与初始模型中未考虑混凝土包含大量普通钢筋有关。

由表3、表4可知:修正后的模型静力位移与实测位移数据更加接近。以跨中的8号测点为例,修正前偏差为-6.99%,修正后偏差为0.16%;修正前自振频率最大偏差-12.01%,而修正后自振频率偏差减小为-1.74%。故修正后的有限元模型能更好地反映出结构实际受力情况。

2 换索敏感性分析

为保证换索过程中结构的安全性,换索前应了解拆除各拉索对结构力学性能的影响程度,即换索的敏感性[7,16]。基于此,笔者选取具有代表性的拉索进行分析,分别选取“卸除1#、15#、28#、41#、55#索”等5个工况,各工况均卸除上游拉索,下游拉索保持不变。选取这5个工况的边、中跨不同位置斜拉索进行分析,分析了不同区域单根斜拉索更换时对结构受力的影响程度,为后续制定换索方案提供依据[16]。以主梁卸索位置为原点,绘制各卸索工况的主梁位移增量如图10;主梁应力增量如图11;主梁索力增量如图12。

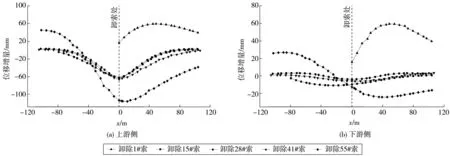
图10 主梁线形增量Fig. 10 Linear increment of main beam

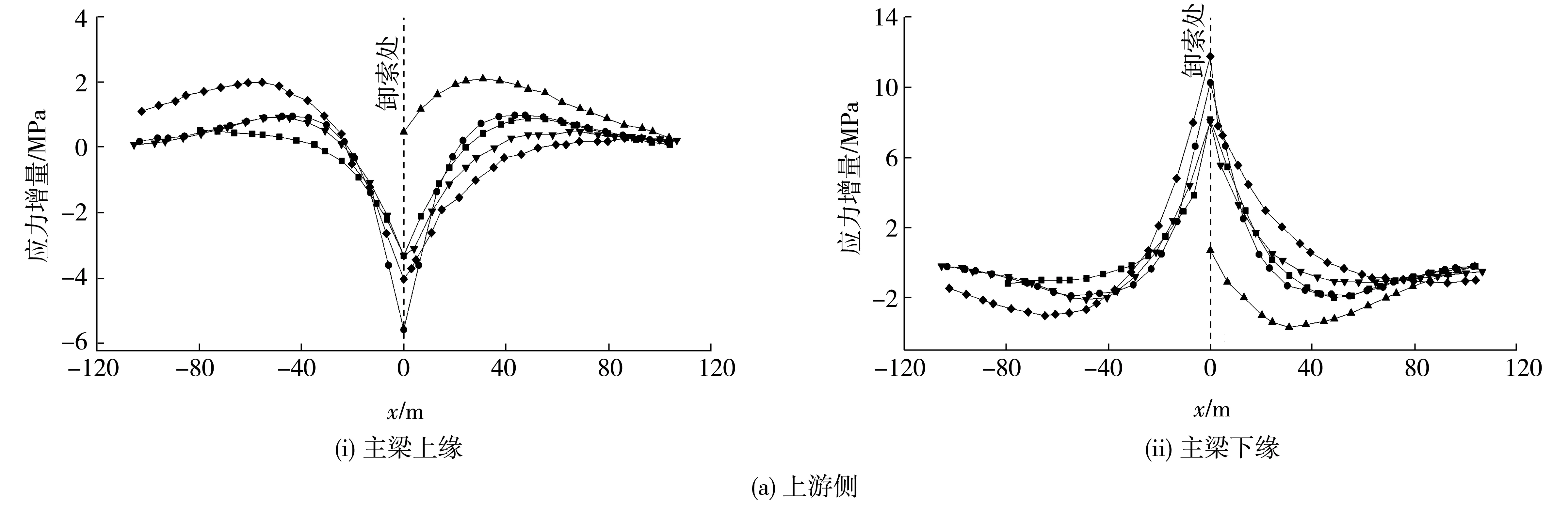
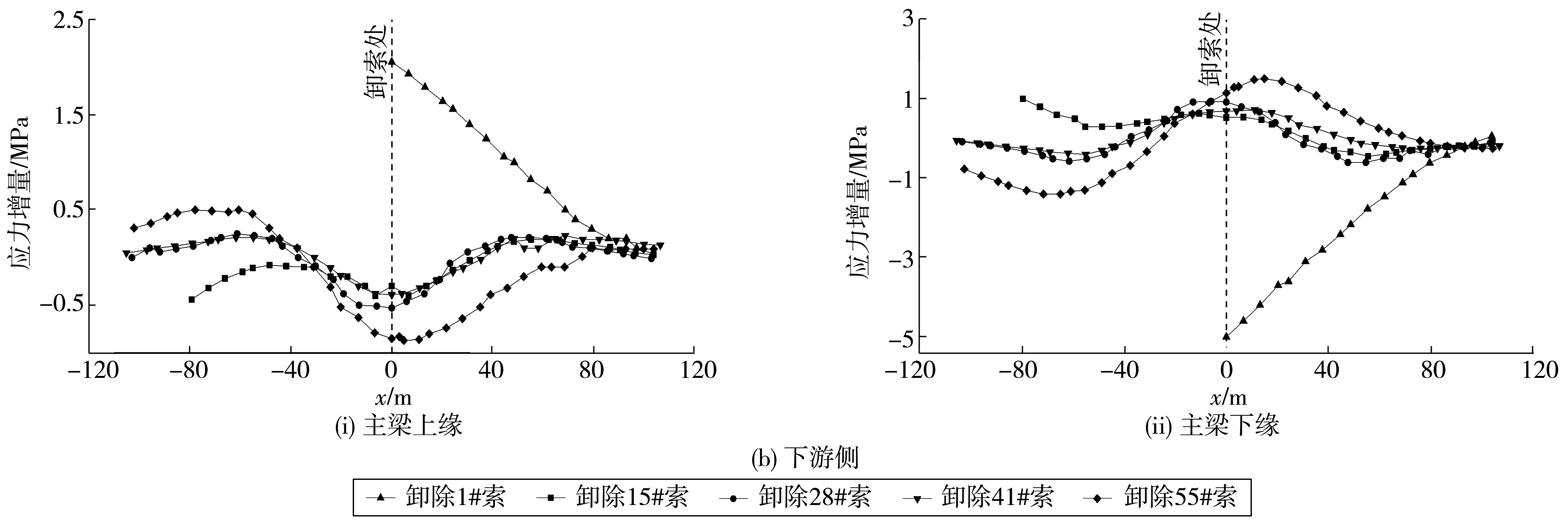
图11 主梁应力增量Fig. 11 Stress increment of main beam

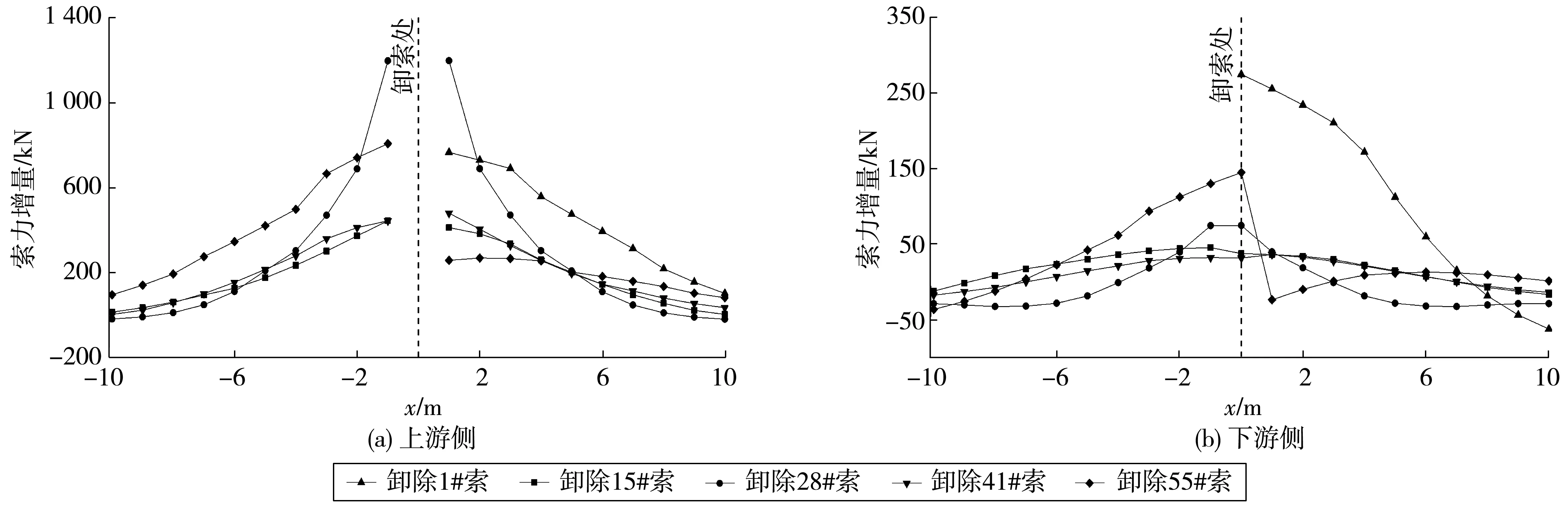
图12 主梁索力增量Fig. 12 Cable force increment of main beam

卸除拉索后,上游侧拉索索力均有不同程度增加,索力增量随距卸索位置距离增大而减小,下游侧索力变化相对较小,卸除28#拉索时增量最大,约1 196 kN。各工况卸索引起的主梁最大位移均在卸索处,下游主梁位移变化量相对较小,影响区域在距卸索位置80 m内,卸除55#拉索时主梁变形较大。拆除拉索将引起卸索位置附近主梁上缘压应力增加,下缘拉应力增加,在卸索侧尤为明显,最大应力增量可达11.0 MPa,出现在卸除55#拉索工况时。对混凝土主梁而言,剧烈的应力变化可能会导致梁底出现拉应力,进而导致梁底开裂,故施工过程中应重点关注主梁应力变化情况。

3 换索方案

3.1 方案拟定

根据上述分析可知:主梁拉应力是换索的主要制约因素,结合该桥的受力特点,设计不同换索数量、上下游对称或交叉换索等换索方案进行对比分析。结果表明:全桥按同一模式换索可能会造成主梁应力严重超限,因此应在不同位置采用不同的换索数量和换索顺序[6]。

最后确定的换索方案为:从桥塔向两侧方向换索,不同区域采用不同的换索方式,具体换索情况见图13、表5。换索方案主要从换索时减小主梁拉应力角度出发,若在跨中区域主梁拉应力极易超限情况下,该区域更换拉索时每次在中跨范围只更换一根拉索,上下游拉索不同时更换,左右侧两桥塔拉索不同时更换。这样既最大限度地降低主梁拉应力也兼顾了换索效率。

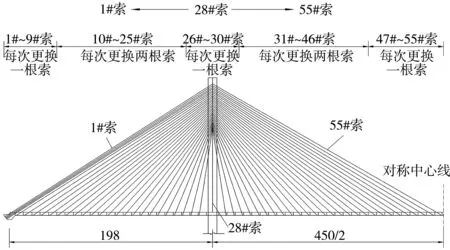
图13 换索顺序示意(单位:m)Fig. 13 Schematic diagram of cable replacement sequence

表5 换索方案Table 5 Cable replacement scheme

3.2 结果分析

相对于成桥状态,整个换索过程中索力增量、主梁竖向位移增量及主梁上下缘正应力增量等包络图如图14;换索过程中主梁上下缘正应力总量包络图如图15。

由图14、图15可知:在更换桥塔处拉索时,相邻拉索索力增量最大,约为1 200 kN;更换中跨跨中处拉索时主梁下挠量最大,约为190 mm;更换桥塔处和中跨跨中处拉索时,主梁上下缘拉压应力均变化较大,约10 MPa;叠加成桥状态恒载应力后,换索过程中中跨跨中截面下缘出现最大拉应力,约为4 MPa,边跨尾端变截面处主梁下缘出现最大压应力,约为26 MPa。依据文献[17],换索工况按短暂状况考虑时,主梁C60混凝土的容许压应力为26.95 MPa,容许拉应力为3.23 MPa,由此可见更换中跨跨中拉索时主梁下缘拉应力仍会超限。

针对换索过程中主梁应力超限问题,需提前采取必要加固措施[18-19](如增设临时索、体外预应力加固、粘接钢板或碳纤维布加固法等)来保障安全。

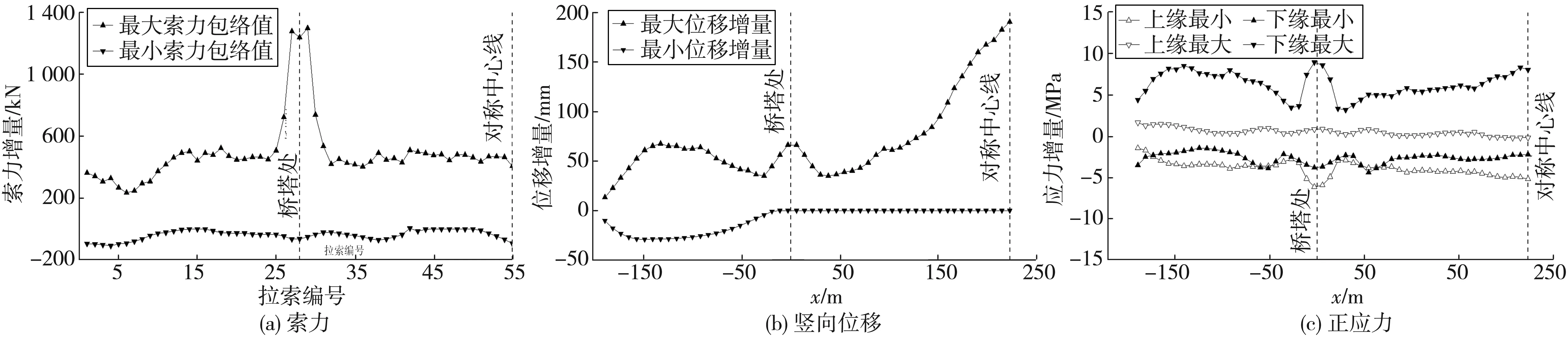
图14 换索过程中主梁各增量包络图Fig. 14 Envelope diagram of each increment of main beam during cable replacement process

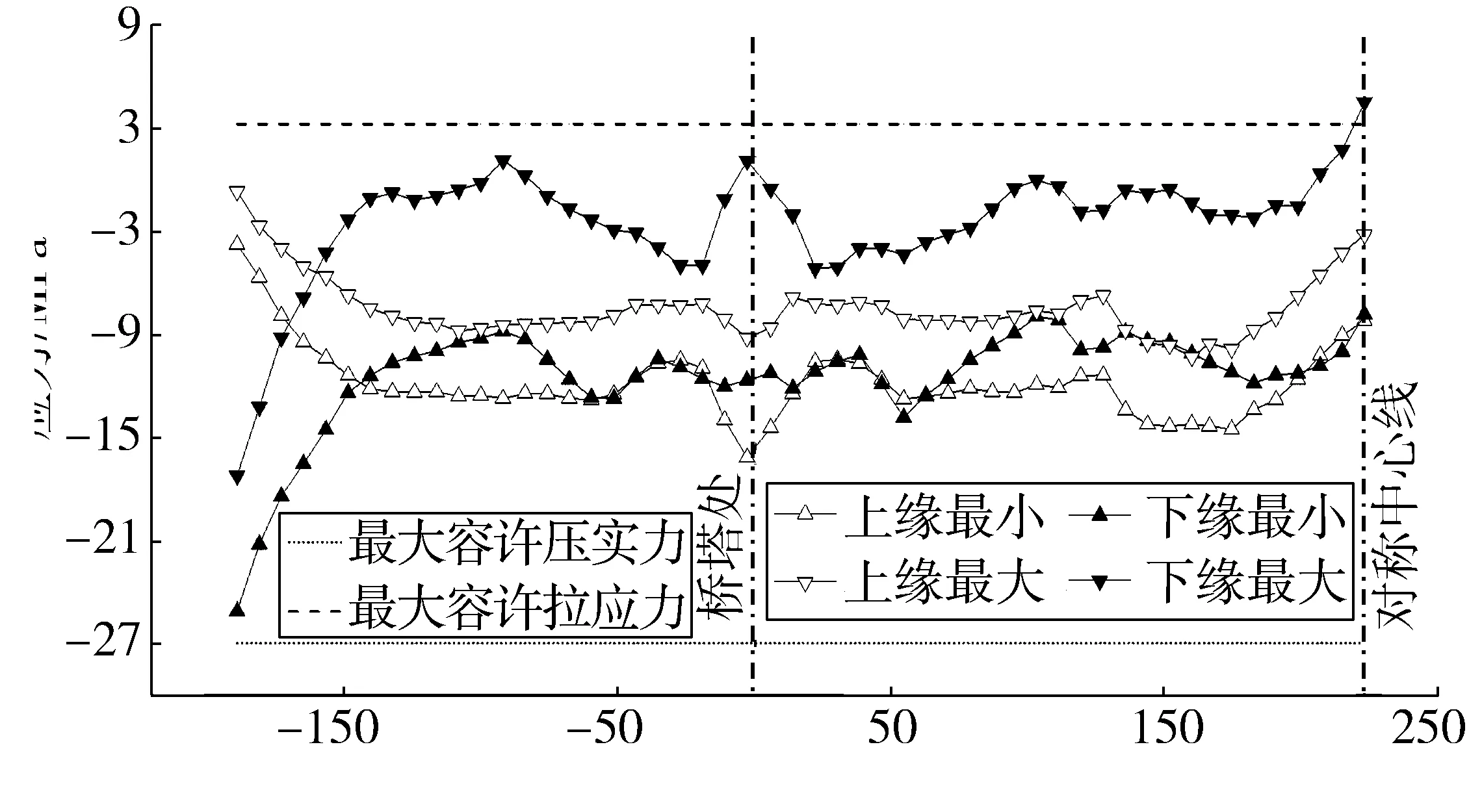
图15 换索过程中主梁正应力包络图Fig. 15 Envelope diagram of normal stress of main beam during cable replacement process

4 结 论

笔者采用联合静动力法对某运营多年的PC斜拉桥进行了有限元模型修正。以实测索力、线形及频率为目标,基于NSGA-Ⅱ算法,得到了Pareto最优解集,采用最大弯曲角法从Pareto最优解集中找到协调最优解,对关键设计参数进行修正,使计算模型接近实际状态;在此基础上,对换索敏感性进行了分析,通过对多种换索方案比较,确定了最优换索方案,得出如下结论:

1)该PC斜拉桥由于受时变效应影响,结构受力状态与成桥时存在一定偏离,需采用适当方法对有限元模型加以修正,笔者所采用的联合静动力法是一种行之有效的修正方法;

2)对于双主肋主梁截面,应采用梁格法建立空间有限元模型,采用单梁模型计算得到的主梁应力误差较大;

3)对于大跨径PC斜拉桥,索距大,梁高低,在桥塔处、中跨跨中附近及靠近梁端的长索处换索时受力较为复杂,应确保结构安全和避免主梁开裂;

4)将换索工况当作短暂状况考虑,更换中跨跨中位置拉索时,主梁下缘拉应力仍超限,换索前应采用必要的加固措施,以保障换索过程的安全。