基于蒙特卡洛随机采样的土石混合体数值模型构建方法
(深圳市综合交通设计研究院,广东 深圳 518003)
0 引言
土石混合体(SRM)是一种非常复杂的不连续介质材料,它是由具有一定尺寸的强度较高的岩块、强度较低的土体和孔隙等组成的多相体系,是一种遍布全国乃至世界许多地方且对工程建设有重要影响的地质材料[1-6]。在工程实际中,构成土石混合体的各种组分在外荷载作用下的力学性质有很大的差异,组分间又存在着极其复杂的相互作用。这种岩土材料的力学性能(如应力传递、破坏模式、裂纹扩展、承载能力等)与均质岩土体有着较大的差别,且块石的空间分布、级配和含石量等关键因素对SRM的宏观力学性质有重要影响[7-8]。因此,有必要对土石混合体的力学特性进行更为准确的分析。最初,学者们多采用试验的方法获取土石混合体的力学性质[9-11],但是在工程尺度上进行土石混合体的原位试验和实验室试验较为困难且耗时[7],数值分析为解决这一问题提供了有效的方法[12]。构建与工程实际符合程度较高的数值模型是目前开展土石混合体数值计算的关键问题[13]。
块石颗粒的生成是构建土石混合体模型的第一步,以往学者多用一些简单的形体来模拟块石。TSESARSKY等[14]基于球形岩石块,研究岩石的弹性模量和各向同性。GRAZIANI A等[15]基于规则形状的岩石块(如圆形、三角形、矩形等)对二维SRM随机模型进行了一系列的数值模拟来研究SRM的力学行为。然而上述方法过度简化了颗粒的真实形态,对具有更为复杂外形的颗粒材料适用性不足。基于此,XU W J等[16-17]和DU C等[18]应用任意凸多边形来模拟块石,这相对于简单形体的块石有很大的改进。罗伟等[19]则基于AutoCAD 二次开发开展了土石混合体随机结构模型生成与直剪强度数值试验研究。喻江武等[6]运用傅里叶变换方法生成特定形状的块石并构建土石混合体模型。赵鑫曜等[20]通过MATLAB软件对大量的块石样本的数字图像进行边界提取、平滑、规则化等处理,得到块石形状坐标和块石形状参数,构建了块石库,从而建立土石混合体模型。这与实际情况比较贴合,但构建块石库需要耗费大量的精力。WANG Z M等[8]提出了一种基于蒙特卡洛随机采样原理生成任意形状随机骨料结构的程序,开展混凝土的细观研究。本文在WANG Z M等[8]的基础上加以改进,分别基于圆形、矩形、三角形采用蒙特卡洛随机采样来进行任意形状二维块石颗粒的构建。
在构建土石混合体模型的过程中,块石间的位置关系判定是极其重要的一个步骤。2个块石在二维平面上的位置关系有相离、接触、相交、内含4种情况。根据自然界的实际情况,在进行土石混合体模型的构建时,需要保证块石之间彼此不能相交和内含[13,16,21]。简单形体间(圆形、三角形、矩形等)的位置关系判定较为简单。XU W J等[16]采用随机凸多边形来模拟块石并基于Area criterion和Sum of the included angle criterion方法进行随机凸多边形块石的相交判定;MENG Q X等[13]基于蒙特卡洛随机采样原理生成任意形状的块石颗粒,但并未对块石颗粒间的位置关系判定方法进行说明,也没有其他学者对任意形状块石位置关系的判定算法进行研究。
本文基于蒙特卡洛随机采样构建的块石,提出了一种任意形状块石的位置关系判定算法,突破了以往在进行块石位置关系判定时对块石“凸性”的限制;介绍了一种构建悬浮结构土石混合体模型的方法,并对其进行了直剪试验分析。
1 任意形状块石颗粒的随机生成
本文基于蒙特卡洛随机采样方法进行二维块石的构建,基本方法是:首先规定一个简单的初始形状(如矩形);然后在初始形状的轮廓上进行点的随机采样,并通过改变采样点与初始形状形心之间的距离来得到一系列不规则形状的块石。具体实现过程如下:
1)生成一组随机角度增量:
{Δθ1,Δθ2,Δθ3,…,Δθn-1}
其中:
(i=1,2,…,n-1)
(1)
且
(2)
式中:ζ、η均是介于0和1之间的系数。当η很小时,表示角度增量很小,随机角度更均匀。
在随机角度增量生成的过程中,需保证:
(3)
3) 求得从原点到随机采样点的距离为{d1,d2,d3,…,dn},对于每一条极径,在di-Δd到di+Δd范围内生成一组新的随机长度序列{D1,D2,D3,…,Dn},则新的极径可以描述为:
Di=di+(2ζ-1)Δd(i=1,2,…,n)
(4)
式中:ζ是0到1之间的随机数;di是简单形体极径的长度;Di是新的极径长度;Δd是极径的变化幅度。
新的随机长度序列{D1,D2,D3,…,Dn}对应一组新的采样点{P1,P2,P3,…,Pn}。
4)在极坐标系中使用{D1,D2,D3,…,Dn}和{Δθ1,Δθ2,Δθ3,…,Δθn}来生成块石轮廓,并使用式(5)将极坐标系转换为笛卡尔坐标系。
(5)
蒙特卡洛随机采样生成块石的过程如图1所示,其中:

(6)
2 块石位置关系判定
2个块石的位置关系有相离、接触、相交、内含4种。本节通过构造包围盒来进行块石位置关系的初步判定,若包围盒相离,则2个块石相离;若包围盒相交、接触或内含,则需通过判断构成2个块石轮廓的线段之间的位置关系来进一步判定2个块石的位置关系。
2.1 基于包围盒的块石位置关系初步判定
包围盒是一个能将复杂形态的块石包围起来的盒子。为了提高算法的效率,迅速排除相离及内含的块石,通过构造包围盒初步判定块石的位置关系是一种较好的方法。
2.1.1包围盒的构建
较为常用的包围盒有AABB(Axis Aligned Bounding Box)包围盒[22]、OBB(Oriented Bounding Box)包围盒[23]和球包围盒[24-25]。AABB包围盒是能够包围原物体的最小轴向包围盒;OBB包围盒则在AABB包围盒的基础上考虑了物体的朝向;球包围盒则是能够包围原物体的最小圆形。图2直观地显示了三者的区别。
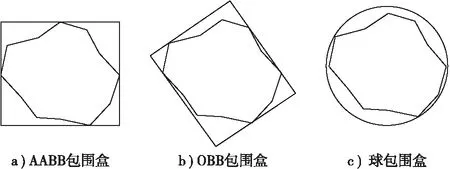
图2 3种包围方式对比
就构造方式来看,AABB包围盒最简单,球包围盒次之,OBB包围盒最复杂;就包围盒与块石的符合程度来看,OBB包围盒最为紧密,球包围盒次之,AABB包围盒最为疏松。考虑到算法的效率,选用AABB包围盒进行块石初步位置关系的判定。
AABB包围盒的构建方法如图3所示,可以得到包围盒1的4个顶点坐标:A1、B1、C1、D1和两边长:d1x=x1max-x1min,d1y=y1max-y1min。同理可以得到包围盒2的4个顶点坐标:A2、B2、C2、D2和两边长:d2x=x2max-x2min,d2y=y2max-y2min。
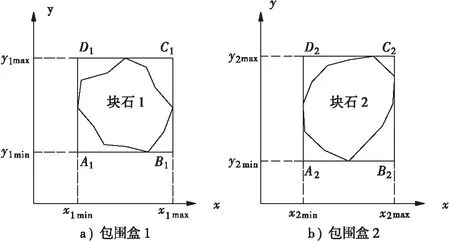
图3 AABB包围盒构建
2.1.2包围盒位置关系初步判定
得到2个块石的包围盒之后,通过构造能将2个块石同时包围的公共包围盒(如图4所示),来判定2个包围盒相离、接触、相交、内含4种位置关系。

图4 AABB包围盒位置关系判断
具体方法如下:首先提取出公共包围盒的2个边长:dx=xmax-xmin,dy=ymax-ymin,其中:xmin=min(x1min,x2min);ymin=min(y1min,y2min);xmax=max(x1max,x2max);ymax=max(y1max,y2max)。然后采用以下条件进行2个包围盒位置关系判定。
1) 当d1x+d2x>dx且d1y+d2y>dy时,则这2个包围盒相交。
2) 当满足3个条件之一时,2个包围盒接触:
①d1x+d2x=dx且d1y+d2y=dy;
②d1x+d2x=dx且d1y+d2y>dy;
③d1x+d2x>dx且d1y+d2y=dy。
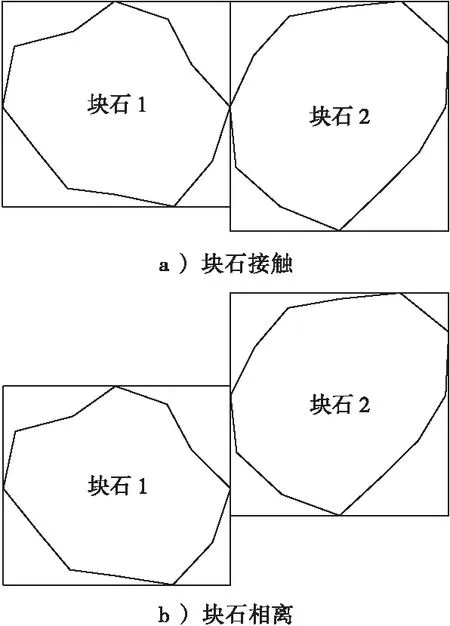
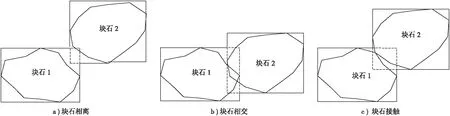
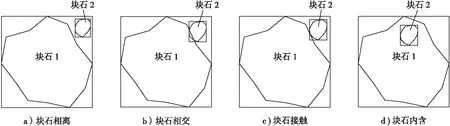
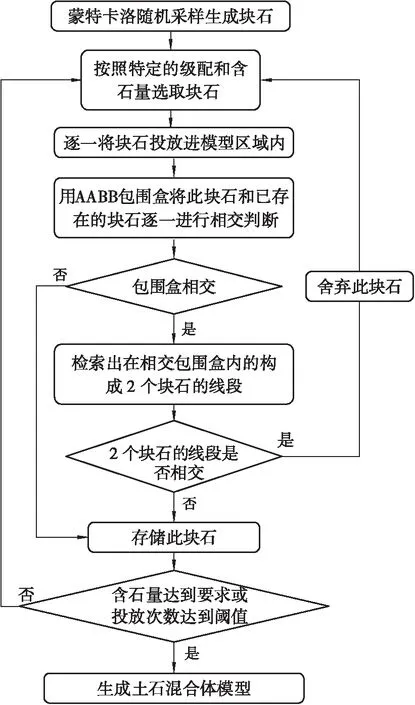
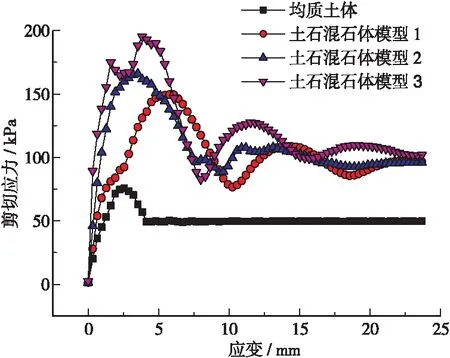
3) 当d1x+d2x 4) 当满足下列情况之一时,2个包围盒内含。 ①x1min>x2min,x1max ②x2min>x1min,x2max 块石位置关系有相离、相交、接触、内含4种情况,具体判定方法如下: 1) 若2个包围盒相离,则2个块石必定相离。 2) 若2个包围盒接触且接触面上2个块石也接触,则2个块石相接触,如图5a所示;否则,2个块石相离,如图5b所示。 3) 若2个包围盒相交,先求出2个包围盒的相交包围盒(定义为2个包围盒的相交部分,图6中虚线部分),然后遍历相交包围盒内构成2个块石轮廓的线段进行相交判断[25]。若相交包围盒构成2个块石的线段均不相交,则这2个块石相离(见图6a);若相交包围盒构成2个块石的线段存在相交的情况,且某块石上存在一顶点在另一块石的内部,则这2个块石相交(见图6b);否则,这2个块石接触(见图6c)。 图5 包围盒接触块石位置关系判断示意图 4) 若2个包围盒内含,同样先构造出2个包围盒的相交包围盒,即为较小的包围盒;若包围盒相交则用“3)”中的方法可以判定出块石的相交(图7b)和接触(图7c);若2个包围盒不相交则判断块石2(较小的块石)是否有一点在块石1(较大的块石)内,若是,则2个块石内含(图7d),否则2个块石相离(图7a)。 图6 包围盒相交时块石相离、相交或接触示意图 图7 包围盒内含时块石位置关系判断 本文基于MATLAB随机生成方法进行土石混合体模型的构建,将蒙特卡洛随机采样生成的块石按照特定的级配和含石量随机投放进指定的区域内[26]。在投放的过程中,采用第2节的方法判定此块石与区域内已有块石的位置关系,当新投的块石与已有块石相离时,判定该块石有效,否则舍弃此块石,重新投放,直至含石量达到要求或投放次数达到阈值[13]。 本文按照特定的级配曲线和含石量在一定区域内进行块石的投放,未被块石覆盖的区域作为土体。在投放时,首先随机生成一个粒径为d(d在限定的范围内)的块石,然后从块石库中随机取出1个块石M(xi,yi), 在前面块石库建立的块石中心o的坐标为: (7) 其中xi、yi为边界上各点的坐标,将各块石以中心o随机缩放,缩放系数为η,然后将块石的中心点坐标o(xo,yo)随机插在区域内的一点s(xs,ys)上,则最终块石在土石混合体区域内的坐标为: (8) 用第2节的方法进行块石的相交、非相交判定,若新插入的块石与已有的块石不相交,则存储此块石,否则,舍弃此块石,重新投放。 在投放过程中,首先设定一个含石率P(定义为块石面积与土石混合体面积的比值)。则对于每一粒径范围内的块石Mi,当Mi达到此粒径范围内块石的含石率Pi时,Mi投放结束,开始投放下一粒径的块石Mi+1。 由于每次块石的投放点都是随机的,当边坡内的块石数量达到一定值时,可能会出现每次新投放的块石总会与边坡内已有的块石相交的情况。因此,针对这种情况,本文设定了一个阈值,当投放次数达到此阈值时,即使没有达到规定的含石率,依然终止投放。 本文建立悬浮结构土石混合体边坡的详细流程如图8所示。 图8 土石混合体模型构建流程图 本文使用MIDAS GTS来对悬浮结构的土石混合体进行网格划分。首先将MATLAB生成的土石混合体模型导入CAD并保存为dxf文件;然后将dxf文件导入MIDAS进行有限元网格划分;网格划分好后,将模型在MIDAS中沿垂直模型平面的方向拉伸1 mm,形成1个假三维模型。 本节共构造3个土石混合体模型(见图9),3个模型级配不同,但尺寸与含石量均相同(含石量为40%)。模型级配如图10a所示,级配3土石混合体模型中大粒径块石颗粒的含量最多,级配2次之,级配1最少。模型尺寸、边界条件及加载方式见图10b,计算用土石材料参数见表1。 采用FLAC3D对土石混合体与均质土体进行直剪试验,其计算结果如图11所示。计算结果表明:均质土体的剪切带为一条规则的直线;土石混合体的剪切带则更加宽厚和曲折,且土石混合体在剪切过程中存在着明显的绕石效应,即塑性区沿着块石之间的土体部分进行扩展。 a)模型1 b)模型 c)模型3 图10 级配曲线与模型试验条件 a)均质模型b)土石混合体模型1 c)土石混合体模型 2d)土石混合体模型3 实验所得土石混合体和均质土体的剪切应力与剪切位移关系曲线如图12所示。 图12 土石混合体与均质土体剪切应力-应变曲线 由图12可得:在剪切的初始阶段,均质土体的剪切应力随剪切应变线性增长,此时土体处于弹性变形阶段;在弹性变形阶段之后、到达峰值强度之前,曲线增长速率不断减小,曲线段逐渐变得平缓,即进入初始屈服阶段;在初始屈服阶段,土体的剪切应力继续增加,达到峰值后,土体发生破坏,其剪切应力开始降低,并逐渐达到相应的残余应力。这与XU W J等[1]和GONG J等[4]的研究结果一致。相比均质土体,土石混合体剪切过程中还会存在若干个局部剪切阶段,即应力-应变曲线呈现多次上升、下降,这是因为土石混合体中存在着块石与块石、块石与土体之间的摩擦、咬合、滑动等情况。由图12可知,局部剪切阶段可能会发生在峰值应力出现前,也可能发生在峰值应力出现之后,并且不同土石混合体模型局部剪切阶段出现的时间和次数均不相同,这可能与块石的空间分布有关。 由于块石的存在,土石混合体内部的相互作用较为复杂,因此,土石混合体的剪切过程较均质土体更为缓慢,到达残余应力时土石混合体的水平位移更大。在剪切的过程中,土石混合体的剪切应力一直大于均质土体,且峰值应力远大于均质土体,这说明块石的存在使得土体的抗剪强度增大,块石对土体强度起到了一种增强作用。另外,通过对不同级配的土石混合体模型进行对比分析,发现在含石量相同的情况下,级配3的土石混合体模型的峰值应力和残余应力最大,级配2次之,级配1最小。这说明在含石量相同的情况下,大粒径块石颗粒的含量越多,土石混合体的抗剪强度越高,即大粒径块石颗粒的存在有助于提高土石混合体的抗剪强度。 本文采用蒙特卡洛随机采样进行块石随机生成,并基于AABB包围盒提出了一种任意形状块石位置关系判定算法,可以有效处理以往研究中在块石位置关系判定方面对块石凸性的限制。基于该算法进行土石混合体模型构建并对3种级配不同、含石量相同的模型进行直剪数值试验分析,结果表明: 1) 均质土体剪切带为一条规则直线,土石混合体剪切带由于块石的存在而变得更加宽厚和曲折。土石混合体剪切带上存在明显绕石效应,即塑性区沿块石之间的土体部分进行扩展。 2) 相比均质土体,土石混合体剪切过程剪应力-应变曲线除了具有近似线性的弹性阶段、达到峰值强度前的初始屈服阶段、剪切破坏面逐渐形成的剪切破坏阶段、剪切变形持续增加的残余变形阶段4个阶段之外,还会存在若干个局部剪切阶段,即应力-应变曲线呈现多次上升、下降。 3) 土石混合体抗剪强度较均质土体有较大提升,表明块石存在对土体强度起到了一种增强作用。并且在含石量相同的情况下,大粒径块石颗粒的含量越多,土石混合体的抗剪强度越高,即大粒径颗粒的增强作用更明显。此外,土石混合体剪切过程较均质土体更为缓慢,到达残余应力时的水平位移更大。2.2 块石位置关系精确判定
3 土石混合体模型构建
3.1 块石的随机投放
3.2 投放终点的确定
3.3 有限差分数值模型的生成

4 土石混合体直剪试验分析








5 结论

