深部岩石爆破裂纹扩展与不耦合装药系数的关系
陈啸林,张智宇,王 凯,彭 磊
(1.昆明理工大学国土资源工程学院, 云南 昆明 650093;2.昆明理工大学公共安全与应急管理学院, 云南 昆明 650093)
爆破过程中,介质最终的断裂效果取决于裂纹的发展过程,裂纹控制是爆破控制的重要研究内容之一[1]。例如,在石油、页岩气开采等领域,需要采取有效的方法促进裂纹扩展。国内外相关学者开展了许多裂纹扩展研究,虽未取得重大突破,但仍有许多值得借鉴的成果。Bendezu 等[2]提出了一种基于有限元的数值方法,模拟了爆炸裂纹的传播过程。杨仁树等[3]通过室内模拟试验,对高应力条件下炮孔穿透层中裂纹的起裂、扩展等动态力学性能进行了研究。田浩帆等[4]研究发现:在初始地应力条件下,岩石爆破过程中,裂纹扩展形成的压碎区呈椭圆形,压碎区的半径随地应力的增加而增大。岳中文等[5]采用一种新型激光动态焦散线试验装置,对单向围压下切缝药包在爆破过程中爆生裂纹的力学性能进行了试验研究。刘超等[6]利用RFPA2D-Dynamic 软件,对不同地应力状态下煤体中裂纹的扩展进行了研究,并对裂纹的发育、扩展及贯通情况进行数值模拟。不耦合系数指的是炮孔直径与药卷直径之比,可通过改变药卷直径控制。徐颖等[7]分析了不耦合系数与爆破作用之间的关系,通过设计相应的试验验证了理论,研究结果表明,不耦合系数为1.67 时,裂纹扩展长度最长,且裂纹数与不耦合系数之间存在一种反比关系。程健[8]基于ANSYS 仿真模拟软件,建立了煤体爆破的数值模型,并分析了不耦合系数等爆破参数,研究发现,爆破近区的破碎圈面积随不耦合系数的减小而增大,裂纹数和密度也随不耦合系数的减小而增大。霍晓锋等[9]采用ANSYS/LS-DYNA 进行模拟,设计了单孔炸药在不同不耦合系数下的破坏方案,结果表明,在不耦合系数为1.65 的情况下,炸药破坏效率良好,保护区范围较小,开掘区域有更多的爆裂产生,与此同时,在爆破中炸药的能量利用率最高。对于含不同倾斜角度裂隙的介质,其裂纹的动态扩展问题十分复杂,沈世伟等[10]利用数字激光动焦散线模型试验,在双孔同步起爆的情况下,研究了预制不同倾斜角度裂隙的介质的爆生裂纹扩展规律。葛进进等[11]采用一种与硬岩力学特性相符的透明模型材料,进行了双向荷载作用下的爆破试验,研究了裂纹扩展方向与地应力的关系。
不耦合装药的形式被应用于许多场景[12],不耦合系数在爆破控制中是一个关键参数。不耦合系数采用不合理,将会显著影响岩石爆破效果及开采效率。数值仿真技术是一种重要的辅助研究方法,它与理论研究、试验研究一样,获得了越来越多的重视,并在实际工程中得到了广泛应用。随着我国矿山开采深度的增加,地应力对爆破荷载的影响也逐渐增大,其作用不可忽视。然而,有些学者在研究过程中,仅考虑不耦合系数的影响,忽视了地应力的作用。本研究首先简要回顾在数值模拟以及物理模型试验中裂纹扩展研究的现状和成果;其次,从数值模拟、相似试验设计等方面研究深部岩石爆破过程中裂纹扩展与不耦合装药系数之间的关系;最后,基于现场获取的相关参数,选用对应的本构方程,采用三维动力分析软件LS-DYNA 研究初始地应力和不耦合系数对裂纹扩展的影响,以期为爆破工艺的优化和实际应用提供理论依据。
1 工程背景
以云南某矿山为例,顶部埋深800 m,矿床以花岗岩体为核心,呈东北分布。基于现场的勘察数据,对深部地区开展了成矿预测,确定了两处重要矿业普查靶点。为此,通过研究深部岩石爆破裂纹扩展与不耦合装药系数之间的关系进行爆破参数设计,以达到良好的爆破效果,实现高效率的爆破开采。
2 数值模拟方法
以花岗岩为爆炸介质,开展地应力条件下不耦合装药系数对岩石爆破过程中裂纹扩展影响的数值模拟研究。
2.1 材料模型及参数
2.1.1 花岗岩
花岗岩的状态方程采用线性状态方程,本构模型采用Riedel-Hiermaier-Thomamodel(RHT)模型。
线性状态方程的表达式为[13]
式中:p为爆压,K为体积模量, ρ/ρ0为爆炸过程中介质当前密度与初始密度的比值。
RHT 模型考虑了应力张量的第三不变量对损伤面形状的影响。如图1(a)所示,其中,αvoid为孔隙度,当压力低于孔隙压碎压力pcrush时,假设材料为弹性材料;之后,压力不断增加,当多孔材料被完全压实时压力为pcomp,该过程是塑性的。塑性变形过程中,对于给定的应力状态和加载速率,只有当荷载超过其屈服极限时,材料才发生屈服。同时,该模型嵌入了与压力相关的弹性极限面方程、失效面方程和残余强度方程,如图1(b)所示,其中,σ 为应力,D为损伤变量,εp为线性强化段累积等效塑性应变,具体表达式与参数见文献[14–15],破坏面、屈服面以及残余面主要用于描述混凝土在冲击荷载作用下的初始屈服强度、失效强度及残余强度的变化规律。损伤变量的表达式为
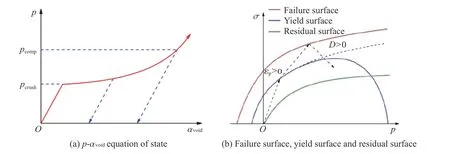
图1 RHT 模型Fig.1 RHT model
式中:εp为线性强化段累积等效塑性应变,为破坏时的等效塑性应变。
花岗岩的参数见表1、表2。表1 中:ρ 为密度,E为弹性模量,ν 为泊松比,σbc为岩石抗压强度,Rm为岩石的抗拉强度,G为剪切模量。表2 中:fc为单轴抗压强度,α0为初始孔隙度,pel为孔隙开始时的压碎压力,βc为压缩应变率指数,βt为拉伸应变率指数,A1、A2、A3为Hugoniot 多项式参数,B0、B1、T1、T2为状态方程参数, ε˙c0为参考压缩应变率, ε˙t0为参考拉伸应变率, ε˙c为失效压缩应变率, ε˙t为失效拉伸应变率,D1为初始损伤参数,D2为损伤参数,B为罗德角相关系数,g∗t 为拉伸屈服面参数,为压缩屈服面参数,A为失效面参数,n为失效面指数,fs∗为剪压强度比,ft∗为拉压强度比,Q0为拉压子午比参数,ξ 为剪切模量缩减系数, εmp为最小失效应变,Af为残余应力强度参数,nf为残余应力强度指数,N为剩余的孔隙度指数。
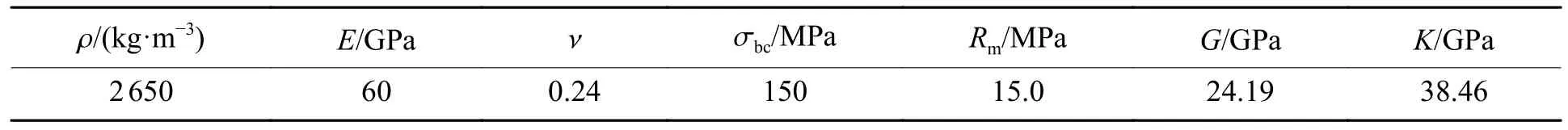
表1 花岗岩参数Table 1 Granite parameters
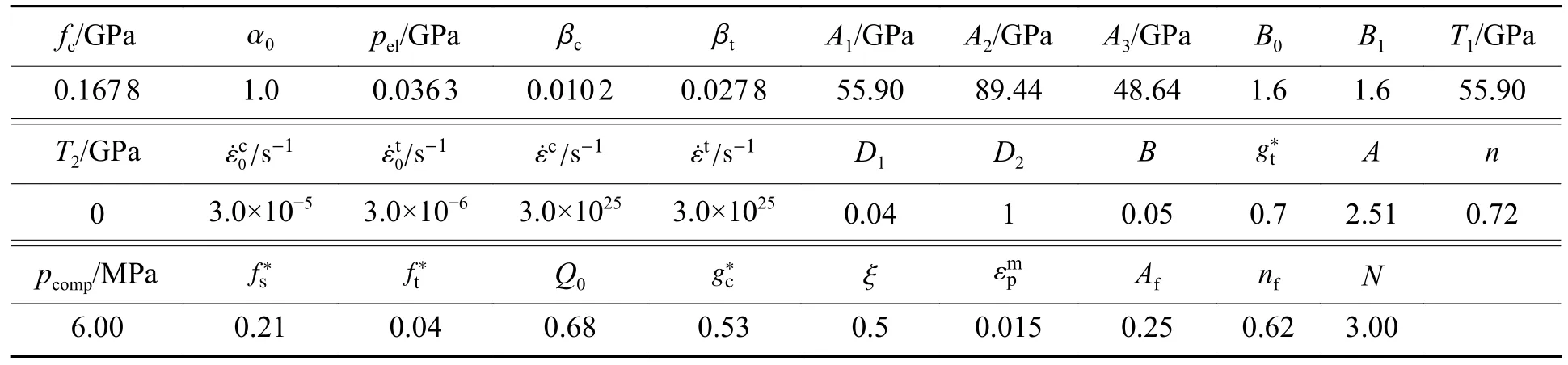
表2 岩石RHT 模型的部分参数Table 2 Some parameters of the rock RHT model
2.1.2 炸药
用JWL 状态方程描述炸药,其表达式为[16]
式中:E0为爆炸产物的初始内能,J/m3;V为爆炸相对体积;Ae、Be、R1、R2、ω 均为常数,取值见表3。表3中,Cd为炸药爆速。

表3 炸药材料和JWL 状态方程参数Table 3 Explosive materials and the JWL equation of state parameters
2.1.3 空气
在不耦合装药数值模型中,药卷四周有一层气体,因此,在仿真模拟时,可以先使用其他关键词替代药卷周围的气体,如*MAT_NULL,在建模结束后,将其参数改变为相应的气体物料。药卷周围气体采用LINEAR_POLYNOMIAL 状态方程描述,表达式为
式中:Eair为空气单位体积内能;μ为比体积,μ=1.4;C0~C6为方程系数,C0=C1=C2=C3=C6=0,C4=C5=0.4。
2.2 数值模型的建立
如图2 所示,建立的模型尺寸为480 cm×400 cm×1 cm(长×宽×厚,分别对应x、y、z轴上的尺寸),两炮孔沿中心水平轴线布置,并关于x=240 cm 对称,孔距为80 cm,炮孔半径为4 cm。利用LS-DYNA进行前处理建模,采用映射方法划分模型。双孔同时起爆,模型四周设为非反射边界以模拟无限域岩石,求解时间设为1 000 μs。在耦合装药方式下,首先,在无地应力情况下观察岩石双孔爆破过程中裂纹扩展情况;其次,假设模型四周施加的围压荷载σx=σy,围压荷载随着时间先线性增加后稳定至20 MPa(见图3,加载末期,地应力的计算式见式(5)),观察施加等围压荷载后地应力对岩石双孔爆破过程中裂纹扩展的影响。此外,在施加等围压荷载的情况下,不耦合系数取1.2、1.4、1.6、1.8、2.0 进行装药,探究不耦合系数对岩石爆破过程中裂纹扩展情况的影响。

图2 有限元模型示意图Fig.2 Schematic diagram of finite element model
式中:σx、σy为水平应力,MPa;H为埋深,埋深约为800 m。
3 数值模拟分析
3.1 耦合装药方式下双孔爆破过程中的裂纹扩展与压力演化
3.1.1 无围压下岩石双孔爆破过程中裂纹扩展与压力的演化过程
图4 给出了无围压下岩石双孔爆破过程中裂纹扩展与压力的演化过程。t=20 μs 时,受双孔爆炸冲击波作用,孔壁环向产生了范围很小的压碎区以及径向微裂纹区。通过力学机制分析可知,压碎区是由于径向压应力超过岩石的抗压强度所造成的,而径向微裂纹区是由于环向拉应力超过岩石的抗拉强度所致[17]。冲击波向外传播,当t=40 μs 时,岩石在拉伸应力的作用下形成径向裂纹。随后,径向裂纹继续扩展,两压力波相互接近,t=110 μs 时,两压力波相遇。当t=120 μs 时,应力波叠加处压力增强。随着时间的推移,应力波不断向外传播,可以观察到应力叠加位置的上下移动,当t=180 μs 时,应力叠加位置见图4 的红色区域;当t=200 μs 时,两孔壁周围接近水平的径向裂纹扩展到裂隙区,但并未相遇;t=230 μs 时,裂纹贯通两孔;t=1 000 μs 时,裂纹扩展至整个幅面。
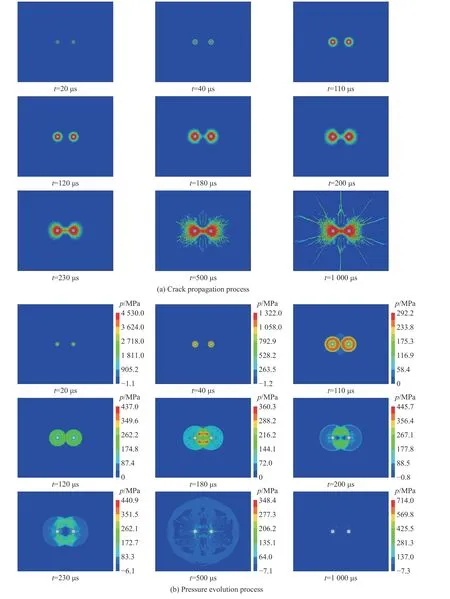
图4 无围压下岩石双孔爆破过程中裂纹扩展与压力的演化过程Fig.4 Crack propagation and pressure evolution processes without confining pressure in rock under double-hole blasting
3.1.2 双向等围压下岩石双孔爆破裂纹扩展与压力演化过程
图5 给出了双向围压均为20 MPa 时岩石双孔爆破裂纹扩展与压力的演化过程。
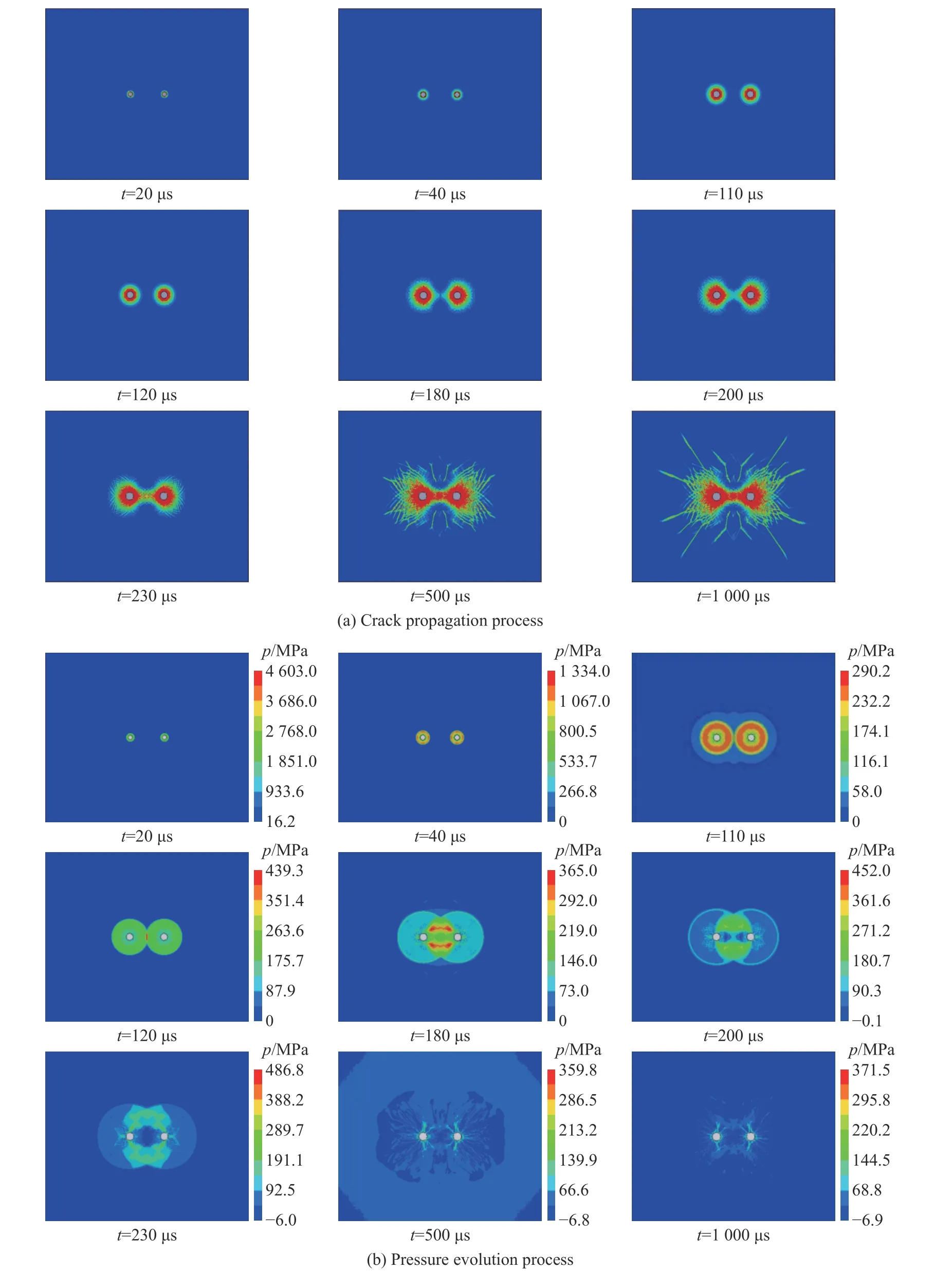
图5 双向等围压下岩石双孔爆破裂纹扩展与压力的演化过程Fig.5 Crack propagation and pressure evolution processes of rock under double-hole blasting with bidirectional constant confining pressure
比较图4 和图5 可以发现:地应力从零升至20 MPa 的过程中,粉碎区的形态基本保持不变,爆破粉碎区近似呈现圆形;加入地应力后,粉碎区的半径有一定的增大趋势;在粉碎区外侧,裂纹以药包为中心沿径向分布,裂纹扩展演化规律在有无围压的情况下基本一致;相比于无围压的情况,施加双向等围压后,在爆炸后期,径向主裂纹的扩展长度明显减小。
为了分析地应力对孔间环向应力的影响,图6 给出了双孔同时起爆条件下,无地应力和施加20 MPa 地应力时监测点A、B在爆破过程中的环向应力时程曲线。监测点A位于爆孔连线的中心,监测点B位于左侧爆孔上方40 cm 处(见图6 中的插图)。对比图6(a)、图6(b)可知:无地应力条件下,A点的环向拉应力峰值和环向压应力峰值分别为25.7 和165.0 MPa,B点的环向拉应力峰值和环向压应力峰值分别为19.8 和137.0 MPa;当施加20 MPa 地应力时,A点的环向拉应力峰值和环向压应力峰值分别为22.3 和281.0 MPa,B点的环向拉应力峰值和环向压应力峰值分别为14.9 和234.0 MPa。以上结果表明,地应力的存在导致爆破环向拉应力减小,在施加地应力的方向上环向压应力显著增大,从而进一步抑制了裂纹的扩展[18–20]。因此,在有地应力条件下,初始地应力场的压力效应对裂纹的产生和扩展起阻碍作用。
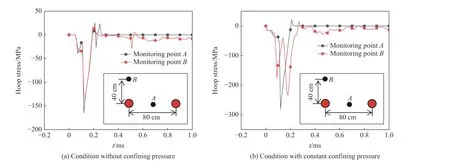
图6 双孔爆破过程中测点的环向应力时程曲线Fig.6 Hoop stress history curves of monitoring points under double-hole blasting
3.2 双向等围压荷载下不耦合系数对岩石爆破裂纹扩展的影响
3.2.1 不耦合系数对孔壁应力峰值的影响
图7 给出了不耦合系数k为1.0~2.0 的情况下孔壁应力pg时程曲线,其中,k=1.0 对应耦合装药,其余为不耦合装药。由图7 可知:k=1.0 时,孔壁应力峰值达到最大,为2 280 MPa;k=1.2 时,孔壁应力峰值减小至1 270 MPa;k=1.4 时,孔壁应力峰值降低至621 MPa;随着不耦合系数的进一步增大,孔壁应力峰值大幅度降低,当k为1.6、1.8、2.0 时,孔壁应力峰值分别为3 9 5、2 7 1 和191 MPa。因此,不耦合装药时的爆破损伤程度比耦合装药时的爆破损伤程度小,说明较大的不耦合系数不利于爆破破岩作业的开展[21]。
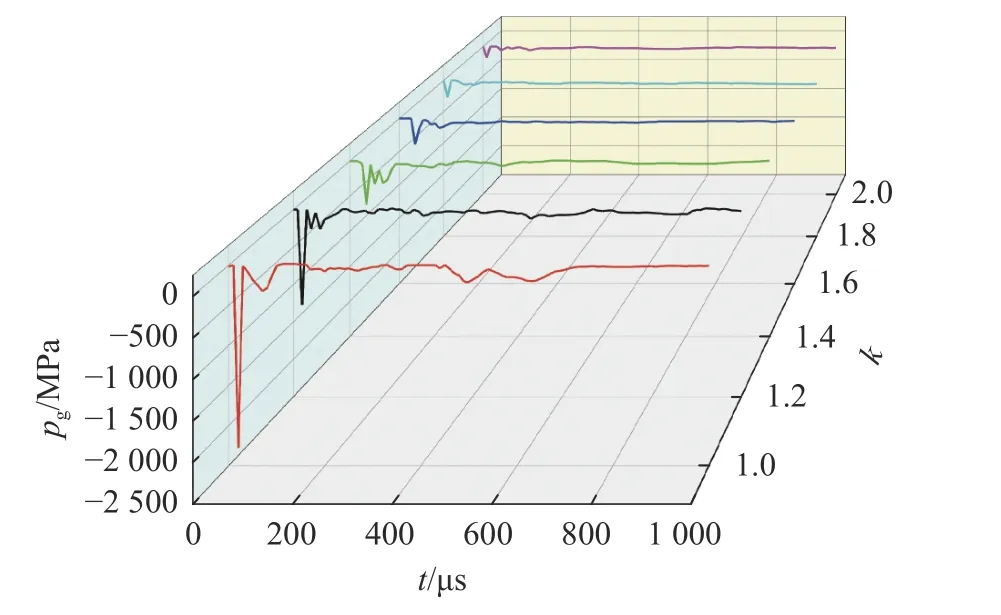
图7 不同不耦合系数下孔壁的应力时程曲线Fig.7 Hole wall stress-time curves under different decoupling coefficients
3.2.2 不耦合系数对粉碎区、环向裂隙区半径以及径向裂纹扩展长度的影响
图8 为不耦合系数k在1.2~2.0 区间时的裂纹扩展情况。由图(8)可知,不同不耦合系数下,爆破后裂隙的发育过程类似,爆炸产生的冲击波压力会超过岩石的抗压强度使其破碎,岩石形成最初裂缝,应力波以炮孔为中心向外传播,爆生气体在应力波的准静态压力作用下进入裂隙,在已有裂隙尖端形成很大的拉应力,裂纹进一步扩展[22]。k=1.2 时,强烈的爆炸冲击波造成炮孔附近区域的岩石破碎,爆生气体对裂纹具有明显的驱裂作用,径向裂纹延伸距离较远。k=1.4 时,裂纹扩展的最大长度明显减小。k=1.6 时,爆破损伤区域随爆炸冲击压力的大幅降低而显著减小,爆生气体对裂纹的驱裂作用减弱,径向裂纹扩展长度进一步缩减。k=1.8 时,仅在炮孔近区产生了极小范围的岩层损伤,爆生气体对裂纹扩展的影响较弱。k=2.0 时,爆炸冲击压力略大于岩石的单轴抗压强度,仅引起炮孔近区花岗岩的起裂,裂纹扩展不明显。
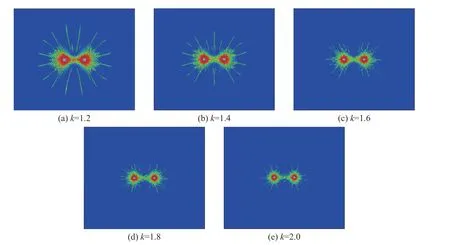
图8 不同不耦合系数下裂纹的扩展情况Fig.8 Crack propagation under different decoupling coefficients
为定量分析不耦合系数对粉碎区半径、环向裂隙区半径以及径向裂纹扩展长度的影响,利用软件的测量功能对模拟结果进行测量,表4 列出了径向裂纹扩展最大长度、粉碎区半径以及沿着x、y、对角线方向(与x、y方向成45°夹角的方向)的环向裂隙区半径。粉碎区属于爆破近区,近似呈圆形,粉碎区沿x、y和对角线方向的尺寸基本相同,故只记录一组数据。
将表4 的数据绘制成图,得到双向等围压下粉碎区半径、环向裂隙区半径以及径向裂纹最大长度随不耦合系数的变化规律,见图9、图10。可以看出,粉碎区半径、最大环向裂隙区半径、平均环向裂隙区半径以及径向裂纹扩展最大长度均随不耦合系数增大而减小。原因如下:不耦合系数增大时,空气介质对爆炸冲击波的衰减作用增强,进而减弱应力波的作用,导致孔壁应力峰值降低,造成粉碎区半径和环向裂隙区半径逐渐减小;同时,此过程中爆生气体引起的准静态压力效应得到增强,但是由于准静态压力效应往往滞后于应力波的作用,裂纹在高地应力条件下仍处于闭合状态,在这种情况下,应力波所引起的径向裂隙很难继续扩展,因此,扩展裂纹的最大长度减小。
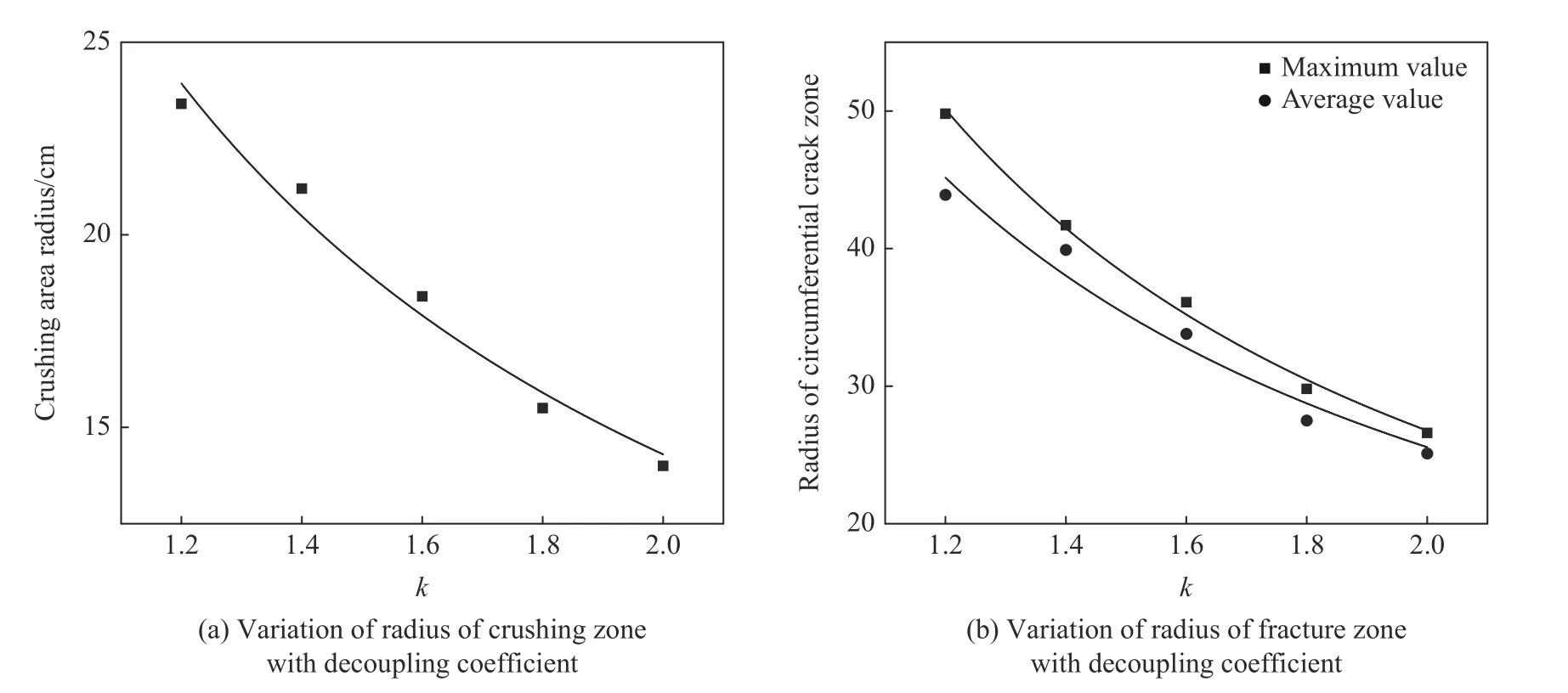
图9 双向等围压下粉碎区半径和裂隙区半径随不耦合系数的变化规律Fig.9 Variation laws of radii of crushing zone and fracture zone with decoupling coefficient under bidirectional constant confining pressure
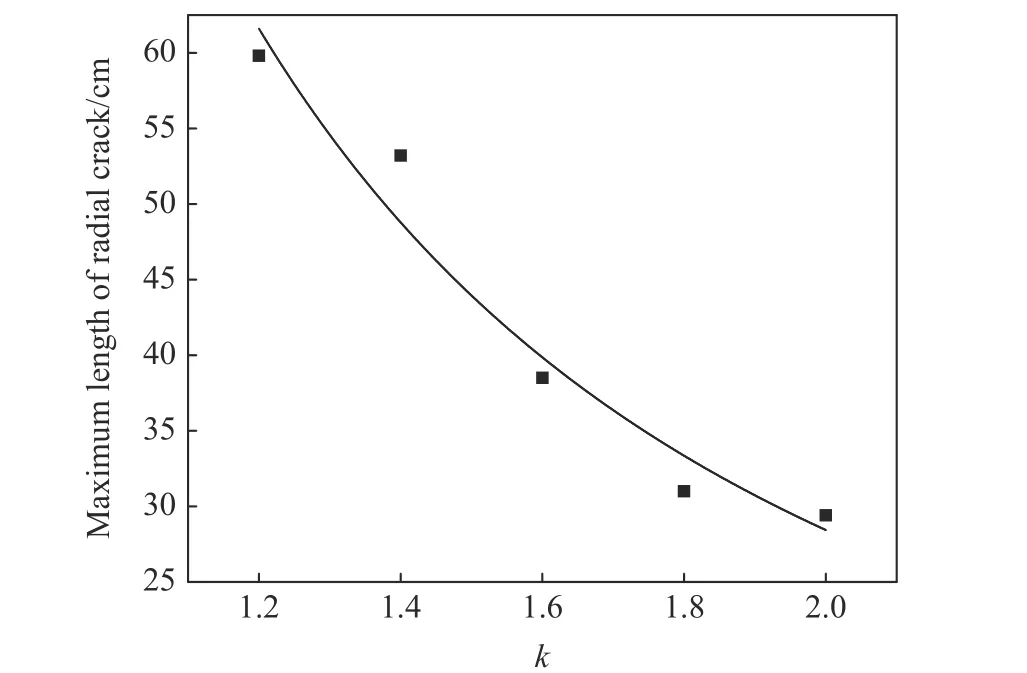
图10 双向等围压下径向裂纹最大长度随不耦合系数的变化规律Fig.10 Variation law of the maximum length of radial crack with decoupling coefficient under bidirectional constant confining pressure
4 动焦散相似试验
Murphy 等[23]将均质岩石与有机玻璃(polymethyl methacrylate,PMMA)进行了等效爆破,二者在爆破荷载作用下的破坏形式基本一致。PMMA 具有良好的光学透明度,通过动焦散试验可以准确地获得PMMA 裂纹扩展形态。本研究通过数值模拟获得了双向等围压荷载下不耦合系数与岩石裂纹扩展特性的关系,为验证研究结果的正确性,开展了PMMA 动焦散相似试验。PMMA 的动态力学参数列于表5,其中:σm为有机玻璃的抗压强度,Cp为纵波波速,Cs为横波波速。

表5 有机玻璃的动态力学参数Table 5 Dynamic mechanical parameters of PMMA
4.1 模型试验的相似性和相似系数
根据相似准则,模型的相似性可归纳为模型的材料相似、几何相似和爆破动力相似[24]。因此,从这3 个方面分析此次试验的相似性和相似系数。
4.1.1 材料相似
模型材料相似系数η 为
本研究中花岗岩的抗压强度为150 MPa,有机玻璃的抗压强度为130 MPa,因此,模型的材料相似系数η 为0.87。
4.1.2 几何相似
依据原型和模型的平衡、几何、物理方程等,各物理量之间的相似关系如下[25]
式中:α 为相似比,下标L、δ、E、ν、γ、σ 代表长度、位移、弹性模量、泊松比、容重、应力,σc为抗压强度,σt为抗拉强度,ε 为应变,下标X、Y、Z代表体积力,C为内聚力, φ为内摩擦角,T为时间。
在尽量减小模型试验失真程度和尺寸效应对试验结果影响的前提下,将模型试件尺寸定为300 mm×300 mm×10 mm,得到几何相似系数αL=16。
有机玻璃的容重γ 为11.8 kN/m3。基于容重相似关系得到容重相似比αγ=2.24,并进一步求得应力相似系数ασ=35.8。
4.1.3 爆破动力相似
试验选用二硝基重氮酚(diazodinitrophenol,DDNP)炸药,其密度约为1 200 kg/m3,爆速可达4.0 km/s。矿山爆破通常选用乳化炸药,其密度为1 150 kg/m3,爆速为4.5 km/s。模型试验与实际爆破所使用的炸药类型不同,“炸药爆炸能量相似”原则[26]要求模型炸药与原型炸药间应满足CρCD=1(Cρ为原型炸药与模型炸药的密度比,CD为原型炸药与模型炸药的爆速比)。根据本研究中的原型炸药和模型炸药参数,可得CρCD=1.08,基本符合“炸药爆破能量相似”原则。
4.2 试验设计
采用有机玻璃板作为模型材料,根据应力相似系数ασ=35.8 以及式(5),求得所施加的围压荷载为0.6 MPa。试验在双向等围压情况下开展,试件材料中心预制一个炮孔,炮孔直径为10 mm,药卷直径可变,分别为8、7、6 和5 mm,相应的不耦合系数k分别为1.2、1.4、1.7 和2.0。为了减小试验误差,各个试件的其他参数保持一致。
4.3 试件爆后形态分析
图11 为双向等围压荷载下试件爆后的形态。图11(a)、图11(b)显示,随着不耦合系数的增大,径向裂纹的扩展范围逐渐减小,图11(c)、图11(d)显示试件仅有少数径向裂纹出现。由此可得,高地应力条件下,较小的不耦合系数有利于裂纹的扩展。

图11 试件爆后的形态Fig.11 Specimen patterns after explosion
为分析径向裂纹扩展长度与不耦合系数之间的关系,对爆后模型试件表面裂纹的扩展形态进行了复刻,如图12 所示。通过对爆后试件进行测量,获得了径向裂纹扩展长度、粉碎区半径和沿着x、y方向以及对角线方向的裂隙区半径,结果列于表6 中。粉碎区属于爆破近区,近似呈圆形,x、y方向以及对角线方向的尺寸基本相同,故只记录一组粉碎区半径数据。
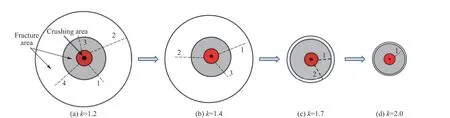
图12 爆后试件裂纹扩展形态Fig.12 Crack propagation morphology of specimen after explosion
从表6 可知,粉碎区半径、最大环向裂隙区半径、平均环向裂隙区半径以及径向裂纹扩展最大长度均随不耦合系数增大而减小,与数值模拟结果一致,进一步证实了数值模拟结果的准确性。
裂纹扩展长度是反映岩石介质爆破效果的一个重要参数,根据表6 中模型试件的测量结果,得到了径向裂纹长度最大值及平均值随不耦合系数的演变规律,如图13 所示。
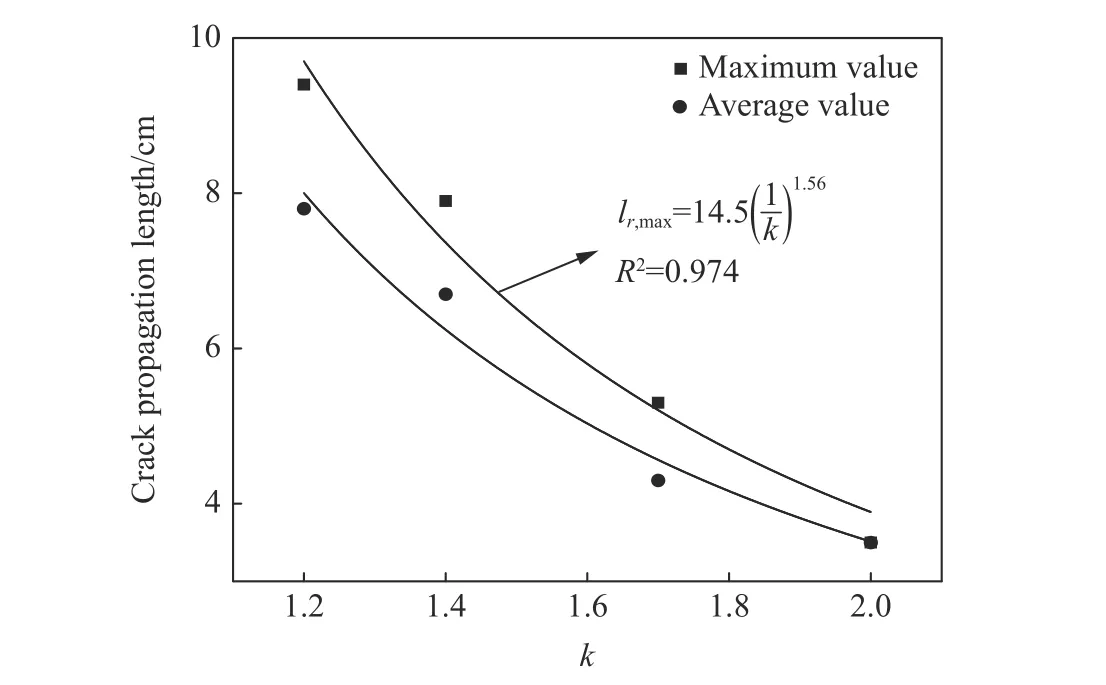
图13 双向等围压下试件径向裂纹长度随不耦合系数的变化规律Fig.13 Variation law of radial crack length of specimen with decoupling coefficient under bidirectional constant confining pressure
由表6 可知,模型试验中,k为1.2、1.4、1.7 和2.0 时的径向裂纹扩展最大长度分别为9.4、7.9、5.3 和3.5 cm。为了提高模型的预测精度,将径向裂纹扩展长度最大值lr,max与不同不耦合系数k采用幂函数拟合,拟合式为
该拟合曲线的拟合精度R2达到0.974。从式(8)能够看出,裂纹长度随1/k的增加而增大。式(8)对于爆破参数设计、实现爆破高效率开采具有较高的参考价值。
5 结 论
通过数值模拟研究了深部岩石爆破过程中裂纹扩展与不耦合装药系数的关系,并通过动焦散相似试验验证了关系的正确性,得到的主要结论如下。
(1) 深部岩体的岩石爆破过程中裂纹的扩展行为与地应力存在明显的对应关系。有地应力条件下的径向主裂纹扩展长度明显小于无地应力条件下,因为在施加地应力的方向上环向拉应力降低,同时,压应力效应增强,抑制了裂纹的扩展。由此可得,在地应力条件下,初始地应力场产生的压力效应对爆破裂纹的产生和扩展起阻碍作用。
(2) 双向等围压荷载下不耦合系数k为1.2~2.0 时岩石爆破过程中裂纹扩展的数值模拟结果表明:随着不耦合系数的增大,粉碎区半径、裂隙区半径、径向裂纹扩展的最大长度以及炮孔孔壁应力峰值均逐渐减小。
(3) 通过动焦散试验建立的不耦合系数(大于或等于1.2 时)与径向裂纹扩展长度间的关系式为lr,max=14.5(1/k)1.56,拟合精度达0.974,拟合效果较好,对于爆破参数设计具有较高的参考价值,对矿山深部开采背景下爆破开采效率的提升具有一定的指导作用。

