基于WOA-XGBoost 模型的胶结充填体强度预测

袁丛祥，刘志祥，杨小聪，郭金峰，万串串，熊 帅，刘伟军

（1.中南大学资源与安全工程学院, 湖南 长沙 410083；2.矿冶科技集团有限公司, 北京 102628；3.国家金属矿绿色开采国际联合研究中心, 北京 102628；4.中钢集团马鞍山矿山研究总院股份有限公司, 安徽 马鞍山 243000）

随着我国浅部矿物开采资源的日渐枯竭，未来矿产资源的开发将聚焦于第二深度空间（1 000～2 000 m），深部硬岩矿山的安全高效开采及造成的环境危害备受关注[1–2]。充填采矿法不仅能够减少尾矿的地表堆积，有效缓解日益突出的矿山环境污染问题，而且能够控制深部开采面临的高地应力问题[3–4]。充填体强度的测定和预测已成为学术界和工业界的研究热点。国内外学者提出了许多预测充填体强度的方法，例如：非线性多元回归、弹性力学分析和人工智能等。韩斌等[5]构建了不同养护龄期的充填体强度与料浆体积分数、水泥含量和灰砂比的多元回归方程。付自国等[6]基于皮尔逊相关性理论，提出了超细尾砂胶结充填体双变量强度模型，并通过进一步耦合养护龄期，构建了三变量强度模型。魏晓明等[7]通过实时监测充填体的三向应力，分析了拱效应和采动应力的运移机制，建立了内部应力预测模型。然而，上述研究仅针对适合特定矿山的充填材料，缺乏一定的泛化能力。

人工智能方法能够有效处理复杂多因素、非线性问题，诸多学者利用人工智能算法建立了充填体强度预测模型。Orejarena 等[8]构建了人工神经网络（artificial neural network，ANN）模型预测胶结充填体耐硫酸盐腐蚀的强度。刘志祥等[9]构建了预测磷石膏和粉煤灰充填体强度的BP（back propagation）神经网络模型，并利用遗传算法（genetic algorithm，GA）对其进行优化，进一步提高了预测精度。Qi 等[10]构建了遗传编程（genetic programming，GP）模型预测胶结充填体强度，并与决策树（decision tree，DT）、梯度提升机(gradient boosting machine，GBM）、随机森林（random forest，RF）3 种机器学习模型进行对比，验证了其预测能力更优。传统机器学习算法存在学习能力差、收敛速度慢和稳定性差等问题[11–12]。因此集成学习模型及其优化混合模型在该领域的应用得到进一步的研究和开发。De-Prado-Gil 等[13]对比分析了RF、GB、XGB、LightGBM 等集成学习方法在预测自密实再生骨料混凝土的抗压强度方面的实用性。Qi 等[14]利用粒子群优化算法调整集成增强回归树（boosting regression tree，BRT）胶结充填体强度预测模型的超参数，得到了预测性能更强的混合PSO-RBT 模型。Xiong 等[15]利用鲸鱼优化算法（whale optimization algorithm，WOA）优化极限梯度提升模型（XGBoost），建立了磷石膏充填体强度预测模型。Lu 等[16]应用梯度提升回归树（gradient boosting regression tree，GBRT）算法，提高了对胶结充填体单轴抗压强度的预测精度，降低了预测误差。

目前，在应用机器学习，特别是应用集成学习模型预测胶结充填体的单轴抗压强度方面已经取得了丰硕成果，但对应用极限梯度提升的混合集成学习模型鲜有报道。基于此，本研究选择固体质量分数、水泥占比和尾砂占比及养护龄期作为输入参数，以充填体试块的单轴抗压强度作为输出参数，研究WOA-XGBoost 混合模型对胶结充填体抗压强度的预测能力，利用WOA 调整XGBoost 模型的超参数，防止过度拟合，实现全局优化。通过与XGBoost、RF 和WOA-RF 模型比较，验证混合模型的预测效果。同时，对输入参数进行重要性分析，确定影响充填体强度的关键因素以及各输入参数的影响程度，以期为矿山充填材料的设计和配比优化提供参考。

1 数据来源与试验设计

1.1 充填材料

试验选用某铅锌矿尾矿库经晾晒的尾砂作为充填骨料。于现场取样的强度等级为42.5 的普通硅酸盐水泥（P.O42.5）作为充填胶结材料，用以改善尾砂胶结充填体的整体性能。使用矿区普通自来水作为充填水，配制不同浓度的充填料浆。对矿尾砂充填料进行物理化学和力学性质测定，以便分析和预测充填体强度。取样后，通过激光粒度分析法进行粒度分析，绘制尾砂粒级组成曲线，如图1 所示。

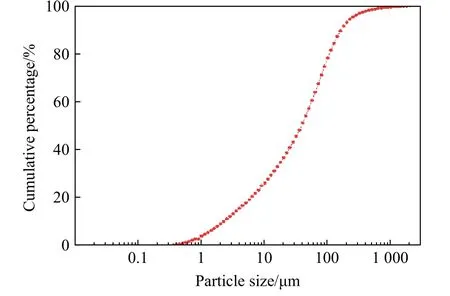
图1 尾砂粒级组成曲线Fig.1 Particle size distribution curve of the tailings

图1 所示分布曲线表明，该铅锌矿的尾砂粒度主要分布在38 μm 以上（占比50%），20 μm 以下占比超过36.8%，整体而言，尾砂粒级适中。试验测得尾砂的物理性质参数和粒径分布如表1 所示。其中：D10、D50、D60、D90分别代表粒级组成曲线上累积占比为10%、50%、60%和90%时对应的颗粒粒径。根据Fu 等[17]、李夕兵等[18]的研究，影响尾砂胶结充填体强度的化学成分主要是阳离子。尾砂的化学成分采用常规化学方法与X 射线衍射法相结合进行测定。采用SIEMENS D500 型X 射线分析仪测定尾砂化学成分，测定结果如表2 所示。

表1 分级尾砂的物理性质和粒径分布Table 1 Physical property and particle size distribution of classified tailings

表2 尾砂化学成分（阳离子）Table 2 Chemical components of the tailings (cations) %

1.2 充填试验设计

为避免偶然性，每个测试组制备3 个充填体试块。为了获得测试效果更佳的充填体试块，浇注前在模具内涂抹润滑油以便于脱模。将充填物料（尾砂和水泥）按比例配料，根据设计的不同质量分数加水搅拌180 s 制浆，并注入7.07 cm×7.07 cm×7.07 cm 的标准三联金属试模中，浇注过程中，采用边搅拌边注模的方式，以避免料浆悬浮和产生气泡。模具浇注满后，等待料浆自然沉降，试块经过初凝（1～2 d）、刮平、自立（2～3 d）后进行脱模处理。为模拟井下环境，放入养护箱中进行低温环境养护（养护温度10 ℃，湿度90%），养护天数分别为7、14、28、60 和90 d。

1.3 试验数据分析

达到养护龄期后，对不同固体质量分数、水泥占比、尾砂占比和养护天数的试块进行抗压强度测试。由于充填体强度较低，一般的压力试验机会产生较大的试验误差，因此本研究使用MTS815 液压伺服岩石力学测试系统，对所有试块以0.5 mm/min 匀速加载至试块发生破坏，测定试块的单轴抗压强度（σc）。为确保试验结果的准确性，每个养护龄期取3 个试块的试验平均值作为该龄期的充填体单轴抗压强度。试块单轴抗压强度测试过程如图2 所示，试验方案及测定结果如表3 所示。

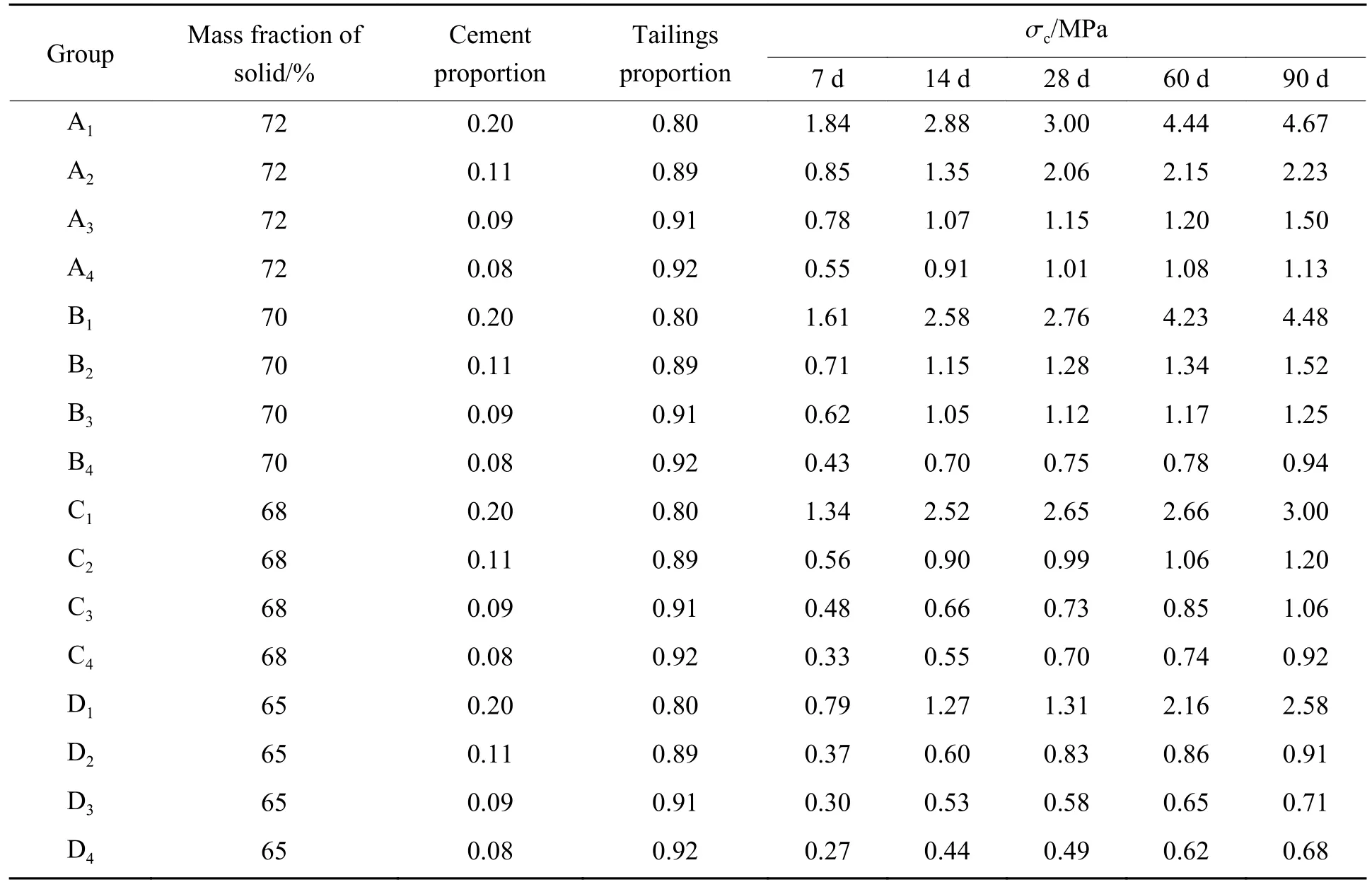
表3 尾砂胶结充填体强度测试结果Table 3 Test results for unconfined compressive strength of cemented paste backfill

图2 试块测试过程示意图Fig.2 Schematic diagram of the test process

由表3 的充填体强度试验结果可知：(1) 水泥是影响充填体胶结的关键因素，当固体质量分数一定时，试块抗压强度随着水泥含量的增加而显著提高，当水泥占比为20%时，试块的内部结构比较致密且黏结性好，强度达到各养护龄期的最大值；(2) 试块单轴抗压强度随养护天数的增加而增大，且固体质量分数越高，增长幅度越大；(3) 充填体强度与质量分数存在一定的相关性，在相同配比条件下，试块的单轴抗压强度随着料浆浓度的增大而提高。

2 方法与原理

2.1 WOA

WOA 是Mirjalili 等[19]提出的一种模拟座头鲸群体狩猎行为的元启发式优化算法。与其他算法不同的是，WOA 采用随机搜索代理的方式来模拟捕猎行为，实现了全局搜索。这种特殊捕猎方法被称为气泡网捕食法，即座头鲸沿着圆圈或“9”字形向上游动并不断释放气泡包围猎物[20–21]。该行为可以总结为包围猎物、气泡网攻击猎物和随机搜索猎物3 部分。

(1) 包围猎物

WOA 预先将狩猎目标或者接近最优搜索代理的位置假定为猎物目前最佳候选位置。其余个体会实时更新自己相对于最佳代理的位置，数学表达式为

式中：t为当前迭代次数，X(t) 为当前搜索代理的位置向量，X∗(t) 为当前最佳搜索代理的位置向量，A和C为系数矩阵。A和C的计算公式为

式中：r1、r2为 [0,1] 的随机向量，a在 [0,2]线性递减。

(2) 气泡网攻击猎物（开发阶段）

座头鲸的气泡网攻击行为分为收缩包围和螺线位置更新两种机制。这两种行为同时发生，鲸鱼随机选择缩小绕圈或沿螺旋路径游动，两种方式发生概率均为50%。据此实时更新鲸鱼的位置，数学表达式为

式中：D′=|X∗(t)-X(t)|， 为当前搜索代理与最佳搜索代理位置之间的距离；b为决定螺旋路径形状的常数；l为 [-1,1] 内均匀分布的随机数；p为 [0,1]内的随机数。

(3) 随机搜索猎物（搜索阶段）

不同于开发阶段，每一次迭代，其余搜索代理根据随机选择的搜索代理而非目前最佳搜索代理实时更新搜索代理的位置。迭代过程为

式中：Xrand(t)为随机搜索代理的位置向量。

WOA 算法通过对开发和搜索能力的平衡与转化，突破了其他种群优化算法容易陷入局部最优的局限，实现了全局搜索的优化[19,22]。

2.2 XGBoost 模型

XGBoost 模型的理论基础是分类和回归树的理论，能够非常有效地解决回归和分类问题，属于集成学习模型[23]。该算法在梯度提升决策树（gradient boosted decision tree，GBDT）模型的基础上，改进了目标函数的计算方法，并减少了运算次数。XGBoost 模型的核心在于通过构建新的决策树优化结构，拟合预测结果的残差并优化为预测分数，将每棵树的预测分数求和作为预测模型的预测值。

数据集D={xi,yi} 包含n个样本，每个样本有m个特征，样本的预测得分由每棵树的得分累加得到，表达式为

式中：K为回归树的数量，F为回归树空间，fk(x) 为第k棵回归树，T为叶子节点（特征）的个数，xi为输入参数， ωq(x)为结构函数q(x) 将输入参数xi映射到各叶子节点T后每棵树的得分。

XGBoost 模型将目标函数的优化问题转化为求解二次函数的最小值问题，并使用损失函数的二阶导数信息来训练决策树模型。为了避免集成模型的过度拟合并生成更简单的树集合，将模型复杂度作为正则项加入目标函数中。XGBoost 模型的目标函数表示为

式中：yi为第i次迭代的实际值；yˆi为对应的预测值；l(yi,yˆi) 为预测值与实际值的误差； Ω(fk)为正则项，用于惩罚树的复杂度。

目标函数的第t次迭代结果为

式中：ft(xi) 表示决策树对应变量xi第t次迭代的复杂度，C为常数。

使用二阶泰勒公式展开损失函数，则目标函数优化为

式中： γ 和 λ 分 别控制叶子节点的个数和分数以调整树的复杂度，gi和hi分别为均方损失函数的一阶导数和二阶导数。

2.3 WOA-XGBoost 混合模型

XGBoost 模型在高效实现GBDT 算法的基础上，将运算速度和准确性提升到极致，但逐级生长策略导致不必要的内存消耗[24]。为了更加快速地获得精确预测结果，本研究通过WOA 优化预测模型的3 个重要参数，即：最大决策树深度（max_depth）、学习率（learning_rate）和L2 正则化系数（reg_lambda）。WOA 优化XGBoost 模型步骤如下：

(1) 对试验数据进行归一化处理，并随机划分为训练集和测试集；

(2) 初始化鲸鱼优化算法，设置鲸鱼的搜索三维空间以及模型参数；

(3) 设置XGBoost 模型待优化参数的范围，生成鲸鱼的初始种群；

(4) 根据所得鲸鱼种群，计算每个鲸鱼位置的适应度；

(5) 对得到的适应度进行排序，定位目前种群的最佳搜索代理，并将其设置为当前全局最佳位置；

(6) 根据式(1)～式(6)更新鲸鱼在各种群中的位置；

(7) 在迭代优化过程中，重复步骤(2)～步骤(6)，以均方误差为适应度函数进行迭代，当迭代次数满足终止条件时，终止迭代并输出最佳鲸鱼位置对应的参数；

(8) 将迭代后的最佳参数（最大决策树深度、学习率和L2 正则化系数）代入XGBoost 模型，得到训练后的最佳预测模型，评估模型性能。

WOA 优化XGBoost 模型的流程如图3 所示，优化后的超参数：最大决策树深度为6，学习率为0.036，L2 正则化系数为0.07。

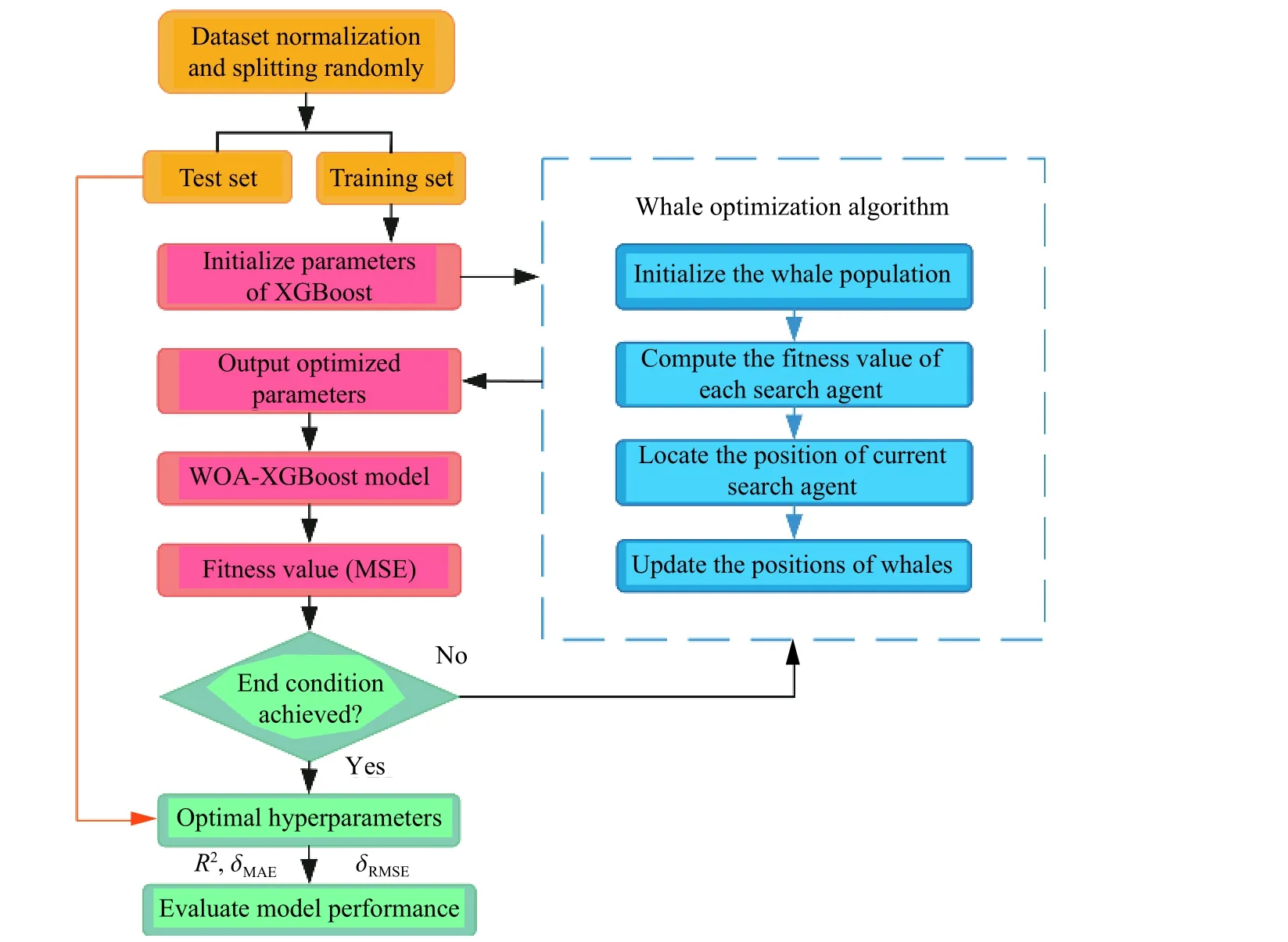
图3 WOA 优化XGBoost 模型流程Fig.3 XGBoost optimization process with WOA

3 结果与讨论

使用该铅锌矿充填体配比试验得到的80 组数据，随机抽取64 组（80%）作为训练集，16 组（20%）作为测试集。选择均方根误差（δRMSE）、平均绝对误差（δMAE）、决定系数（R2）作为性能评价指标，评价WOA-XGBoost 预测模型对训练集和测试集试块单轴抗压强度预测的准确性。计算公式为

式中：n为进行测试和训练的样本数目，yi、yˆi和y¯ 分别为数据的实际值、预测值和实际值的平均值。

δRMSE和δMAE越小，越能体现预测模型对充填体强度预测的准确性。与此相反，采用最小二乘法进行参数估计时，R2越大，回归效果越显著，预测模型越精确。

3.1 WOA-XGBoost 模型预测结果

以数据集的均方误差（δMSE）作为适应度函数，获得WOA-XGBoost 预测模型不同种群大小的适应度变化曲线，如图4 所示。通过跟踪每次迭代的适应度来评估训练集数据迭代时不同种群规模的预测效果。该预测模型不同种群大小的性能参数如表4 所示。

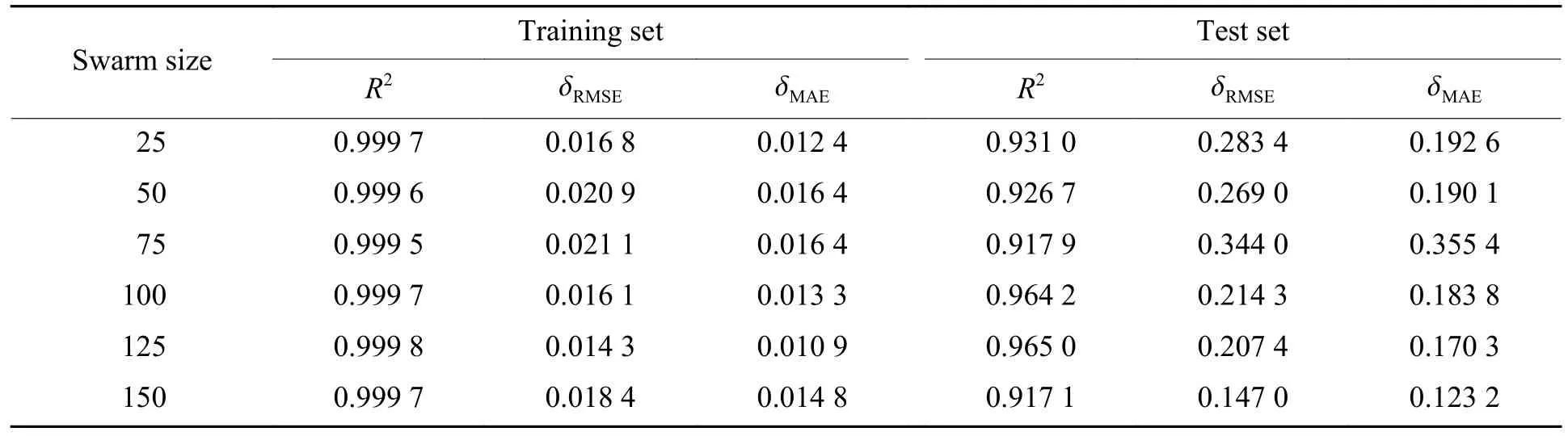
表4 WOA-XGBoost 预测模型的性能参数Table 4 Performance metrics of the proposed WOA-XGBoost model

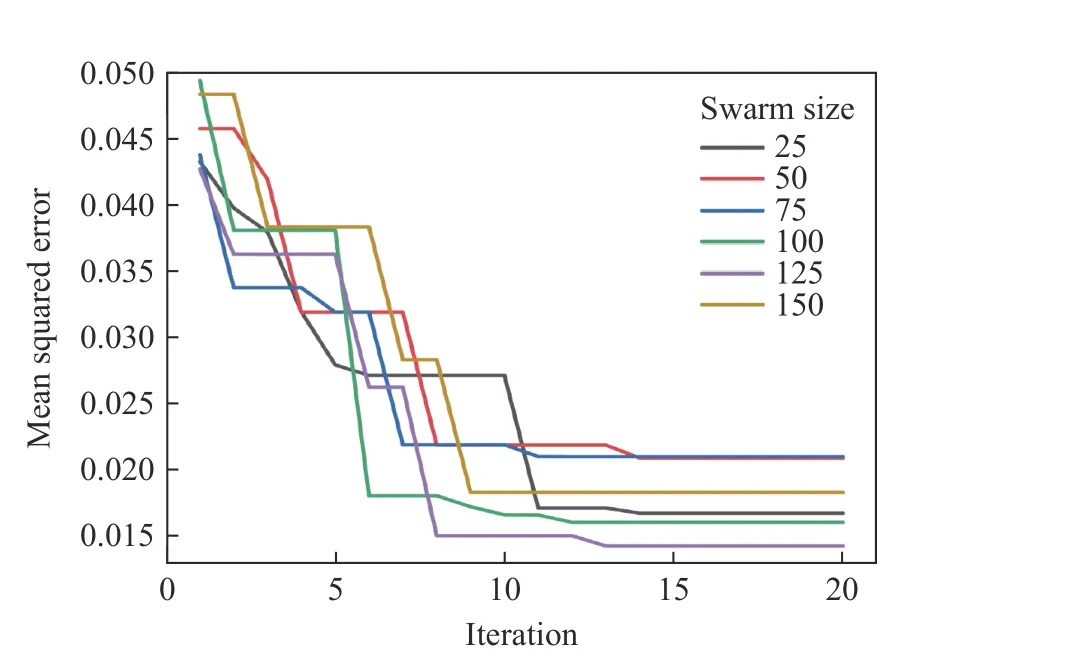
图4 WOA-XGBoost 预测模型不同种群大小的适应度变化曲线Fig.4 Fitness value versus iteration curves of the WOA-XGBoost model with different population sizes

由图4 可以看出，各种群的适应度在前3 次迭代中迅速降低，说明鲸鱼优化算法对极限梯度提升模型的参数优化效果显著。当迭代次数达到14 后，不同种群规模的适应度趋于稳定，特别是种群规模为100 和125 时，收敛速度明显提升。当种群规模达到125 时，模型具有最快的收敛速度，适应度取得最小值0.011，迭代次数为13。

根据表4 记录的数据，训练集的各种群决定系数均超过0.99，且均方根误差不超过0.021 1，呈良好的正相关；测试集的决定系数均超过0.91，证实优化后的混合模型的训练效果良好，产生的误差相对较低。当种群规模为125 时，决定系数最大，测试集误差最小，训练效果显著优于其他种群规模，预测模型能够获得最佳的性能。

WOA-XGBoost 模型预测试块强度的训练集和测试集预测值与实测值结果的对比如图5 所示。训练集中各样本对应的预测值和实测值紧密贴合，测试集只有个别样本的误差较大，整体贴合度良好。对比训练集和测试集的预测表现，证明优化后的混合模型的测试集是经过良好训练的，并且训练集推广到测试集后，WOA-XGBoost 模型能够很好地预测充填体强度，有效降低预测误差。

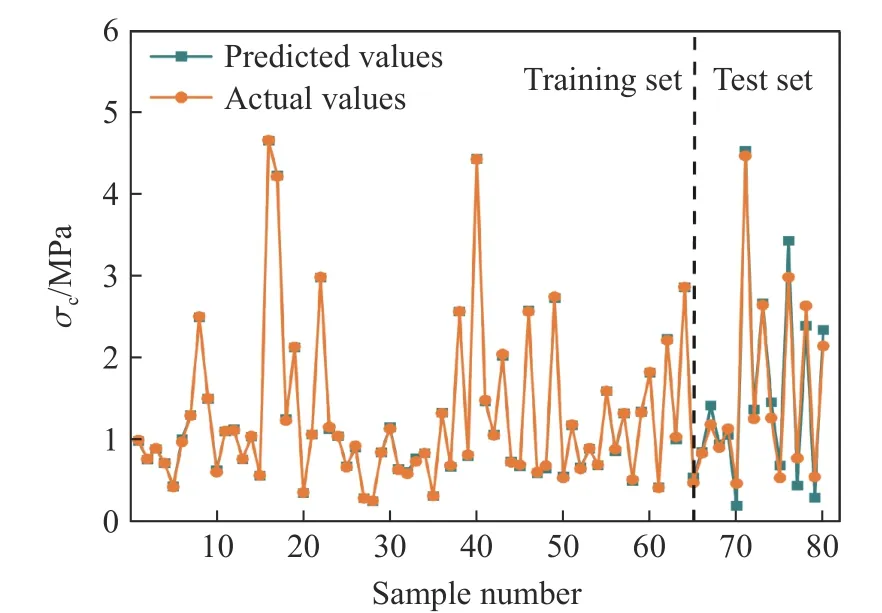
图5 模型训练集和测试集的预测值与实测值的对比Fig.5 Comparison of the predicted and actual values of the WOA-XGBoost model

3.2 与其他模型结果比较

为了进一步研究WOA-XGBoost 模型的学习能力和预测效果，以R2、δRMSE和δMAE为评价指标，与XGBoost、RF 和WOA-RF 模型的测试集进行对比，结果见图6。可以看出，与XGBoost 模型相比，WOAXGBoost 模型的δRMSE、δMAE分别降低了49%和31%，R2达到0.965 0，提高7%，证明了WOA-XGBoost 模型对预测试块强度的可行性及准确性。

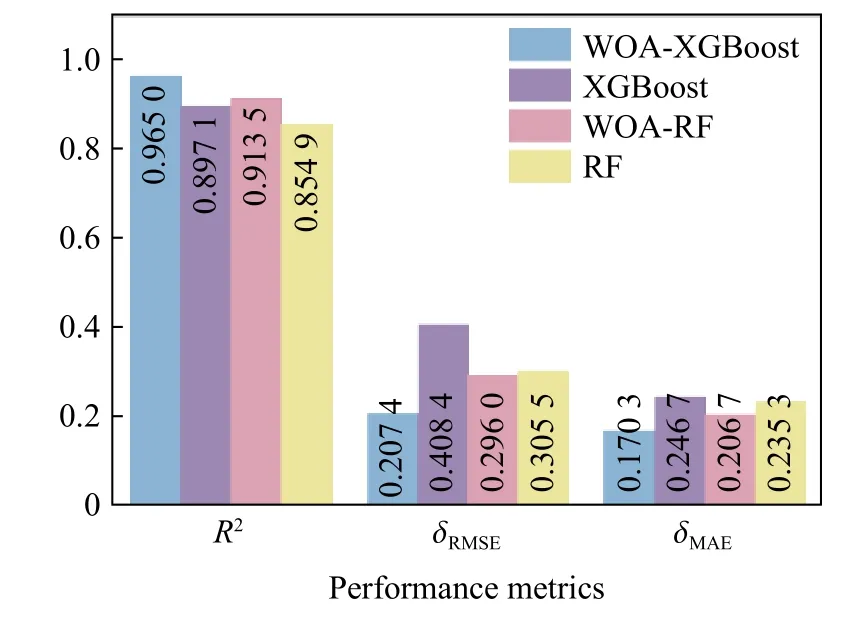
图6 模型的性能评价参数的对比Fig.6 Comparison of performance metrics with mentioned models

图7 显示了4 种模型的训练集和测试集对试块单轴抗压强度的预测值与实测值回归分析结果。通过数据点相对于等值线（预测值等于实测值）的偏离程度衡量试块强度的预测误差，XGBoost 模型和WOA-RF 模型的训练集数据预测值与拟合线较为贴合，但测试集数据点比较分散，且强度越高，离散越明显，个别样本位于误差超过20%的区域。RF 模型数据的预测值和实测值普遍存在一定的偏差。相比而言，WOA-XGBoost 模型的多数数据点完美地集中在拟合线附近，鲜有偏离的数据点，表明预测值的误差较小。对比分析回归结果可知，经过WOA 优化的XGBoost 模型经过良好训练后，能够进一步提高试块强度的预测精度。综上，图6 的评价数据与图7 的数据散点分布相互印证，证明了WOAXGBoost 预测模型强大的泛化能力和精确的预测性能。

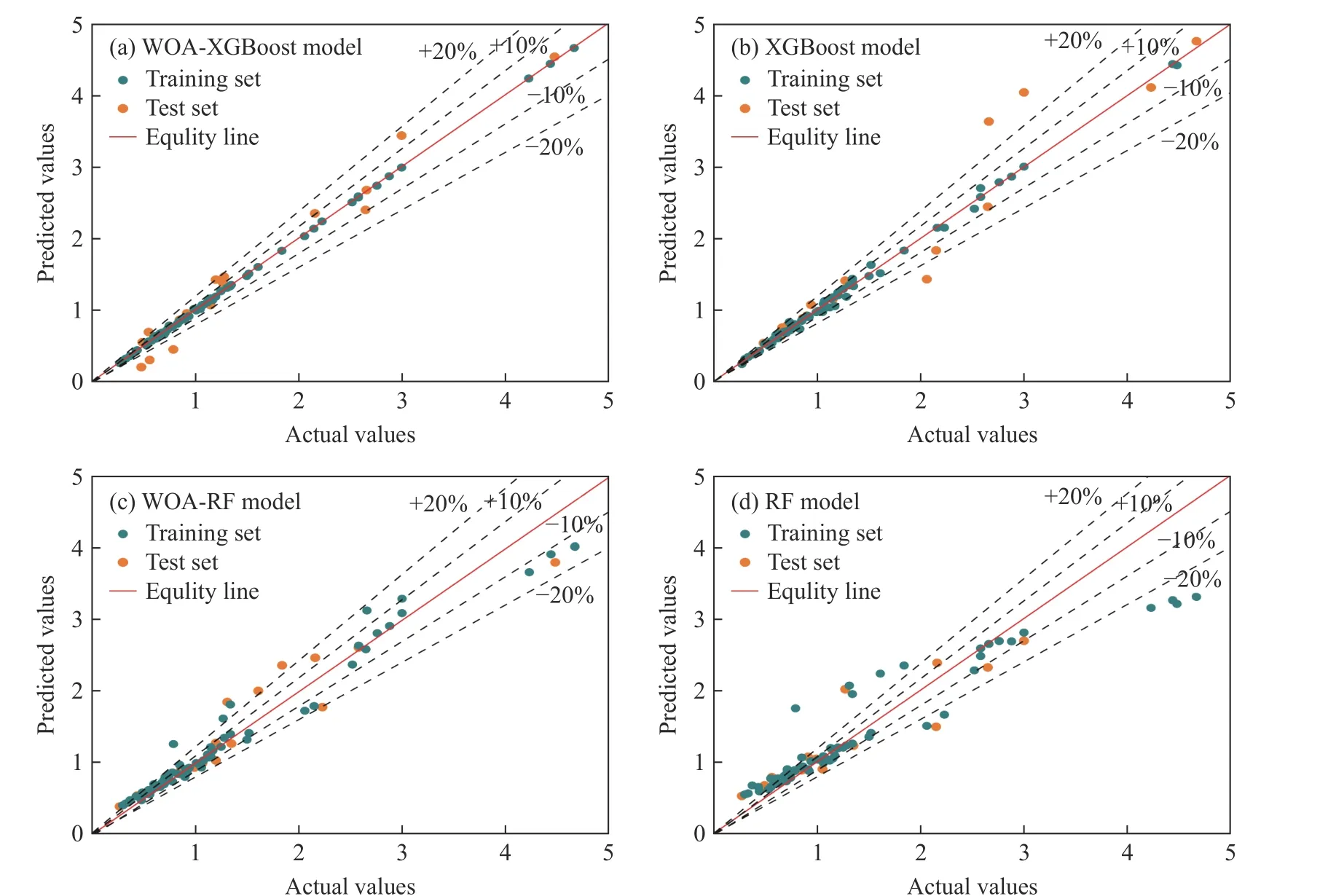
图7 模型的单轴抗压强度预测能力对比Fig.7 Comparison of the compressive strength predictive ability of the developed methods

3.3 输入参数重要性分析

根据表3 显示的试验结果，固体质量分数、水泥占比、尾砂占比和养护天数等输入参数都对充填体的单轴抗压强度有一定影响，为了获得各参数的影响程度，需对各参数作进一步的重要性分析。XGBoost 模型可以自动计算并输出所建立预测模型中的各输入参数的重要性，取10 次计算的平均值作为参数的重要性得分，结果如图8 所示。

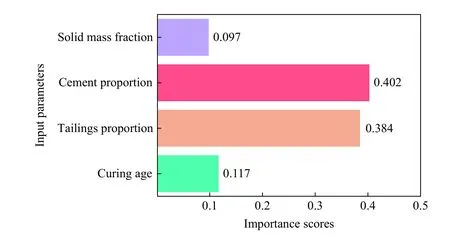
图8 各输入参数的重要性得分Fig.8 Importance scores of the input parameters

从图8 可以看出：水泥占比（重要性得分为0.402）是影响充填体强度的决定性因素，输入参数的重要性得分由大到小依次为水泥占比、尾砂占比、养护天数、固体质量分数，与抗压强度试验结果一致，进一步验证了所建立的WOA-XGBoost 模型的合理性。

4 结 论

(1) 基于某铅锌矿的充填料浆配比试验，提出了WOA-XGBoost 混合预测模型，该模型具有较快的收敛速度，有效降低了预测充填体强度的误差。模型训练集的R2为0.999 8，测试集的R2为0.965 0，证明WOA-XGBoost 模型经过训练后，具有良好的预测精度和泛化能力。

(2) 与单一XGBoost 模型相比，WOA-XGBoost 模型测试集的R2提高了7%，δRMSE和δMAE分别降了低49%和31%，表明WOA 能够有效地优化XGBoost 的超参数。相比于XGBoost、RF 和WOA-RF 模型，WOA-XGBoost 模型的预测性能更优。

(3) 养护天数、尾砂占比、水泥占比和固体质量分数的重要性评分依次为0.117、0.384、0.402 和0.097，揭示了水泥含量对于充填体强度起决定性作用，并且4 个输入参数均为所提出模型的敏感参数，因此在设计充填材料时应予以充分考虑。