含预制裂纹陶瓷圆盘劈裂破坏的离散元模拟

杨 玲，任会兰，赵 涵

（北京理工大学爆炸科学与技术国家重点实验室, 北京 100081）

氧化铝陶瓷价格低廉、来源广泛，且具有熔点高、密度低、强度高等优异的物理力学性能，是一种有广阔发展前景的工程结构材料。在实际应用中，氧化铝陶瓷所处工况往往复杂多变[1–2]，不仅会承受准静态拉压载荷，还可能受到如爆炸、高速碰撞等动态冲击载荷的作用。因此，对氧化铝陶瓷材料在动态载荷下的力学响应及其裂纹扩展规律等开展研究对实际工程应用具有重要意义。

目前，国内外学者针对陶瓷材料的断裂破坏开展了大量研究。Wang 等[3]为降低应力集中效应的影响，将集中力加载改进为均布力加载，并根据Griffith 强度理论将圆盘试件的加载区域加工成平台进行实验[4–6]，从而获得更准确的岩石材料力学性能数据。牛欢欢等[7]通过开展准静态和动态压缩实验分析透明陶瓷玻璃内裂纹的扩展过程，发现裂纹扩展路径是“有选择性的”，裂纹源出现在试件承载能力最低的区域。赵翰卿等[8]利用分离式霍普金森压杆（split Hopkinson pressure bar，SHPB）装置开展了陶瓷巴西圆盘的动态劈裂破坏实验，研究表明，裂纹最先产生于陶瓷圆盘试件与弹性杆接触处。

裂纹的产生和扩展是脆性材料发生破坏的主要原因之一，相关研究受到了众多学者的关注。其中，Horii 等[9]和Nemat-Nasser 等[10]研究了岩石断裂（轴向分裂和剪切断裂）的微观机制，解决了由模型缺陷尖端产生的裂纹引起的弹性边值问题。此外，方敏杰等[11]和宁建国等[12]采用复势函数对受远场载荷作用下椭圆形微裂纹的变形进行求解，探讨了微裂纹初始取向的变化对裂纹尺寸增长的影响，研究发现，翼型裂纹扩展的临界应力随着微裂纹初始尺寸的增大而降低。另一方面，朱万成等[13]利用RFPA 软件模拟了单轴加载下含中心裂纹岩石试件的破坏过程，并将其分为弹性变形、裂纹稳定扩展和主裂纹失稳扩展3 个阶段。杨庆等[14]基于ABAQUS 有限元模拟技术研究了受压条件下张开型翼型裂纹的扩展路径；在此基础上，胡荣等[15]通过引爆雷管产生冲击波的方式开展了爆炸应力波入射角对裂纹起裂角和扩展角影响规律的研究，结果表明，翼型裂纹的起裂角和扩展长度均受到入射角的影响。

离散元法是专门用来解决不连续介质问题的数值模拟方法，从微观结构的角度研究材料的力学特性，能够准确模拟脆性材料的动态破坏和裂纹扩展过程。近年来，研究人员采用离散元法研究了玻璃、岩石等脆性材料内裂纹的扩展规律。例如：赵永等[16]基于离散元法对预制裂纹的花岗岩试件进行单轴压缩加载，发现随着裂纹倾角的增大，裂纹扩展过程由最初的翼型裂纹占主导逐渐转变为次生裂纹占主导；马棋棋等[17]利用离散元软件建立了SHPB 系统，研究了无机玻璃圆柱和圆盘试件在冲击载荷下的动态破坏过程，结果表明，纵向压力、端面摩擦力以及横向惯性力对试件的破坏过程均有影响。

陶瓷材料具有小变形破坏的特征，且高强度、短历时的冲击加载特点使得观测陶瓷材料裂纹扩展过程具有一定的困难。为揭示陶瓷材料在冲击载荷下的碎裂模式和裂纹扩展过程，本研究采用颗粒流PFC 软件建立陶瓷圆盘在冲击加载下SHPB 实验的数值模型，对含预制裂纹的平台圆盘陶瓷试件进行数值模拟，研究不同倾角（预制裂纹与加载轴线角度）对试件破裂模式的影响规律，并结合复合型裂纹尖端应力场揭示翼型裂纹成核和扩展的演化过程。

1 SHPB 实验的数值计算模型

如图1 所示，利用离散元颗粒流数值模拟软件建立陶瓷试件冲击加载SHPB 实验的二维仿真模型，由右至左依次为撞击杆、入射杆、透射杆及能量吸收墙（吸收杆），陶瓷试件放置在入射杆和透射杆之间。其中，1、3、4、5 点为入射波信息采集点，2 点为透射波信息采集点。杆件直径为14.5 mm，入射杆和透射杆长度为430 mm，撞击杆长度为20 mm。

图1 SHPB 二维计算模型Fig.1 Two-dimensional simulation model of SHPB

压杆和氧化铝陶瓷试件材料均采用平节理黏结（Flat-joint）模型，试件与杆件之间的接触则采用线性接触模型，杆件材料[8]和氧化铝陶瓷模型参数见表1。为验证数值计算结果的准确性，表2 给出了陶瓷宏观力学性能参数的模拟结果和实验结果，两者吻合良好，因此可用该计算模型进行模拟计算[18]。

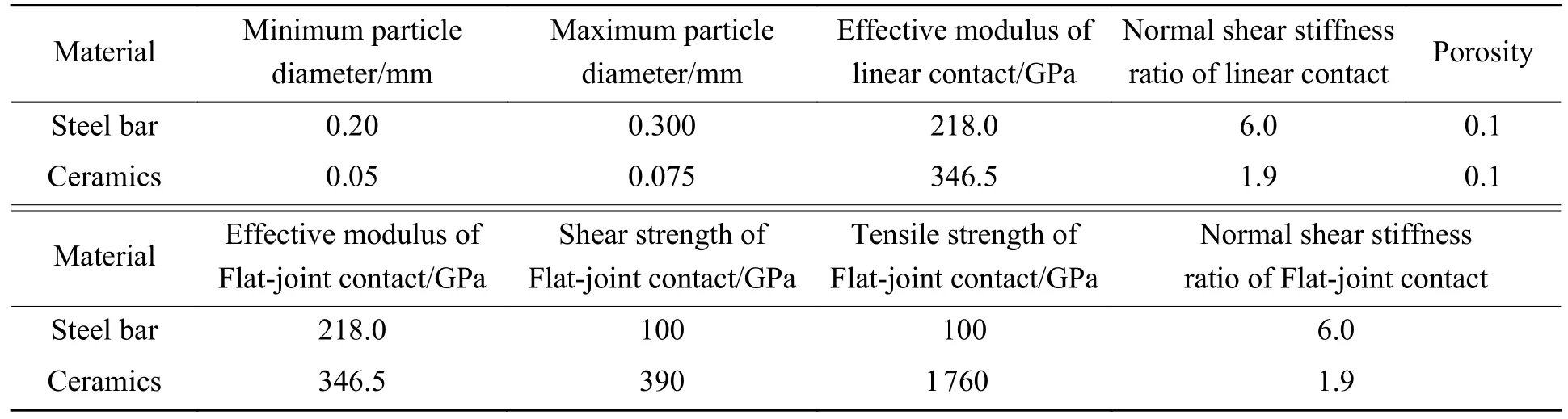
表1 材料Flat-joint 模型的细观参数Table 1 Micro parameters of the Flat-joint model for materials

表2 陶瓷力学性能的数值模拟与实验结果Table 2 Numerical simulation and experimental results of mechanical properties of the ceramics

通过细化杆件端面边界颗粒改善压杆端面与试件的接触情况，使应力波在传播过程中更为均匀。控制撞击杆速度，使入射杆内产生半正弦加载波，并在入射杆与透射杆上设置如图1 所示的测量圆（measure circle），监测应力波在杆件中的传播情况。撞击杆加载速度为35 m/s，加载时间为40 μs。图2 为测量圆监测得到的入射波和透射波数据信息，入射杆在撞击杆的加载下产生近似半正弦的应力波，时长为40 μs。计算结果表明，入射波、透射波与不同测量点入射波的形状和幅值基本一致，说明应力波在传播过程中没有发生明显的弥散现象，因此可以认为计算中采用的SHPB 实验模型是可靠的。

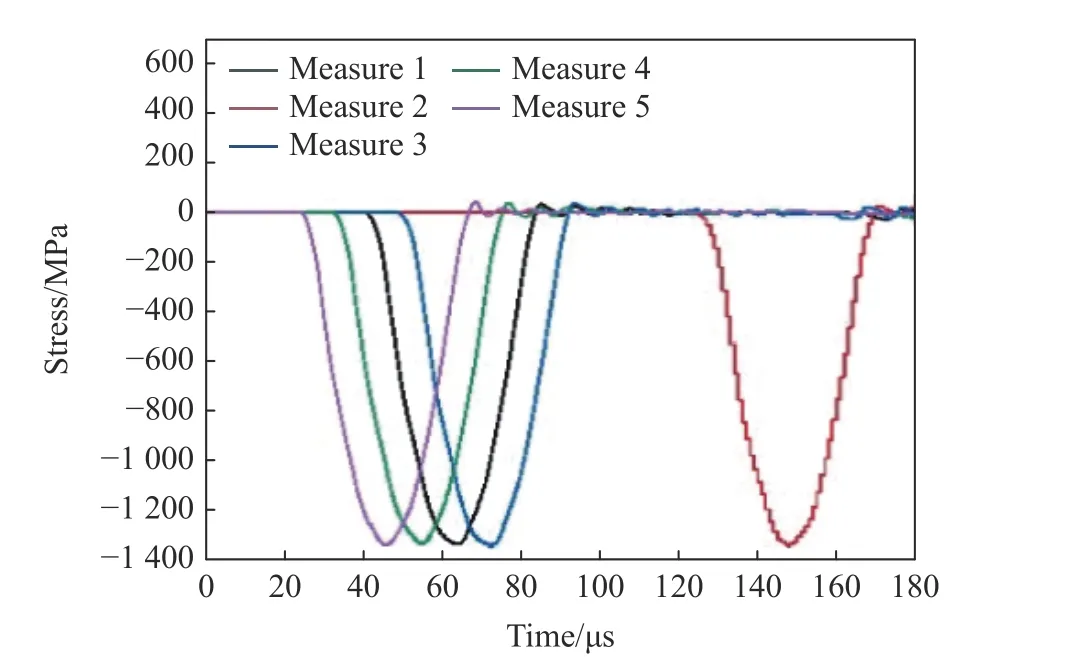
图2 无试件状态下的波形信号Fig.2 Waveform signal without specimen

2 氧化铝陶瓷动态劈裂破坏分析

2.1 动态巴西劈裂破坏的数值模拟

基于图1 建立的计算模型，对 ∅14 mm 的平台圆盘陶瓷试件的破坏过程进行数值模拟。撞击杆速度为12 m/s 时，采集到的入射波、反射波和透射波形，如图3(a)所示。随着应力波的加载，反射波信号在经历一段平台区后开始增大，表明此时试件发生破坏，波阻抗急剧变化，导致反射波的波形陡升。图3(b)显示了陶瓷试件两端轴向应力时程曲线及试件破坏情况，可以看出：t=98 μs 时，平台圆盘试件与压杆接触端面处产生了少量拉伸裂纹（B′点）；t=100 μs 时，试件沿加载方向的中心线上产生主裂纹（C′点）；随着载荷增加，主裂纹继续向试件与压杆接触的两端面扩展（D′点）；t=104 μs 时，轴向加载的应力达到峰值，主裂纹沿圆盘中心轴线贯穿，圆盘试件边缘处产生大量次生裂纹并向中心扩展（E′点）；卸载过程中，次生裂纹遍布整个圆盘试件，试件整体碎裂（F′点和G′点）。

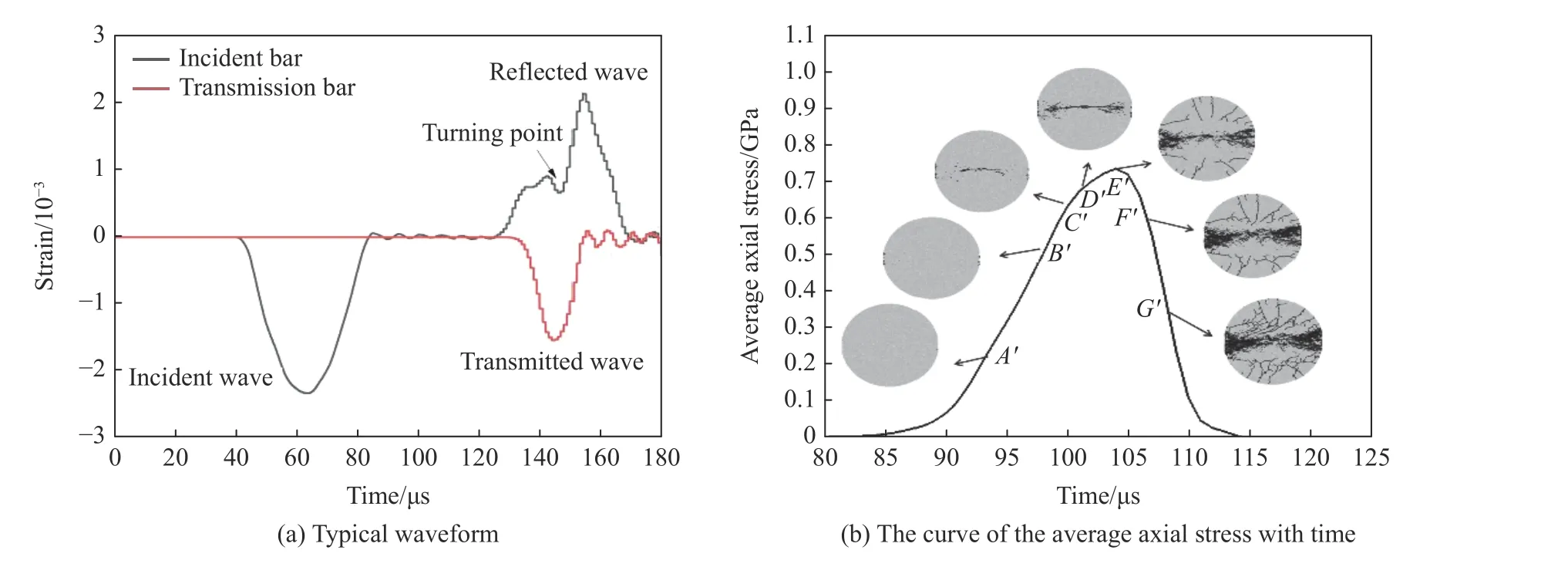
图3 平台圆盘试件动态破坏计算结果Fig.3 Dynamic failure results of platform disk specimen by simulation

2.2 模拟结果与实验结果的对比

采用SHPB 实验技术对陶瓷平台圆盘试件进行冲击加载，并通过Veo7400 Phantom 高速摄影机记录圆盘试件的动态劈裂破坏过程。实验采用60Si2MnA 合金钢压杆系统，撞击杆长度为300 mm，入射杆与透射杆长度均为1 200 mm，压杆直径为14.5 mm，所测A99 陶瓷平台圆盘试件的尺寸为 ∅14 mm×7 mm。

撞击杆速度为12 m/s 时，试验过程中记录的压杆波形如图4 所示。采用波形整形器后，入射波近似为三角波，反射波在上升沿出现一个明显的转折，对应的时间为透射波的峰值时刻，这些特点与数值计算结果（见图3）相似。高速摄影机记录的试件破坏过程如图5(a) 所示，陶瓷试件在t=10.00 μs 时沿加载轴线方向产生一条清晰的宏观裂纹；t=23.33 μs 时，试件加载端附近出现次生宏观裂纹；随着裂纹的扩展，试件呈现轴向劈裂破坏模式。图5(b)给出了试件破坏的离散元计算结果（不同颜色代表不同试件碎块）。可见，拉伸破坏最先产生于试件中部，随着主裂纹的扩展，试件边缘处产生了次生裂纹，这些裂纹扩展汇合，最终导致试件整体碎裂，与实验结果有较好的一致性。

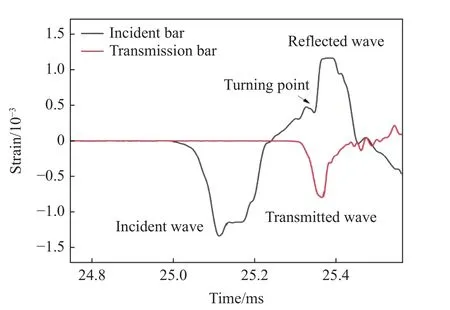
图4 实验波形Fig.4 Experimental waveform

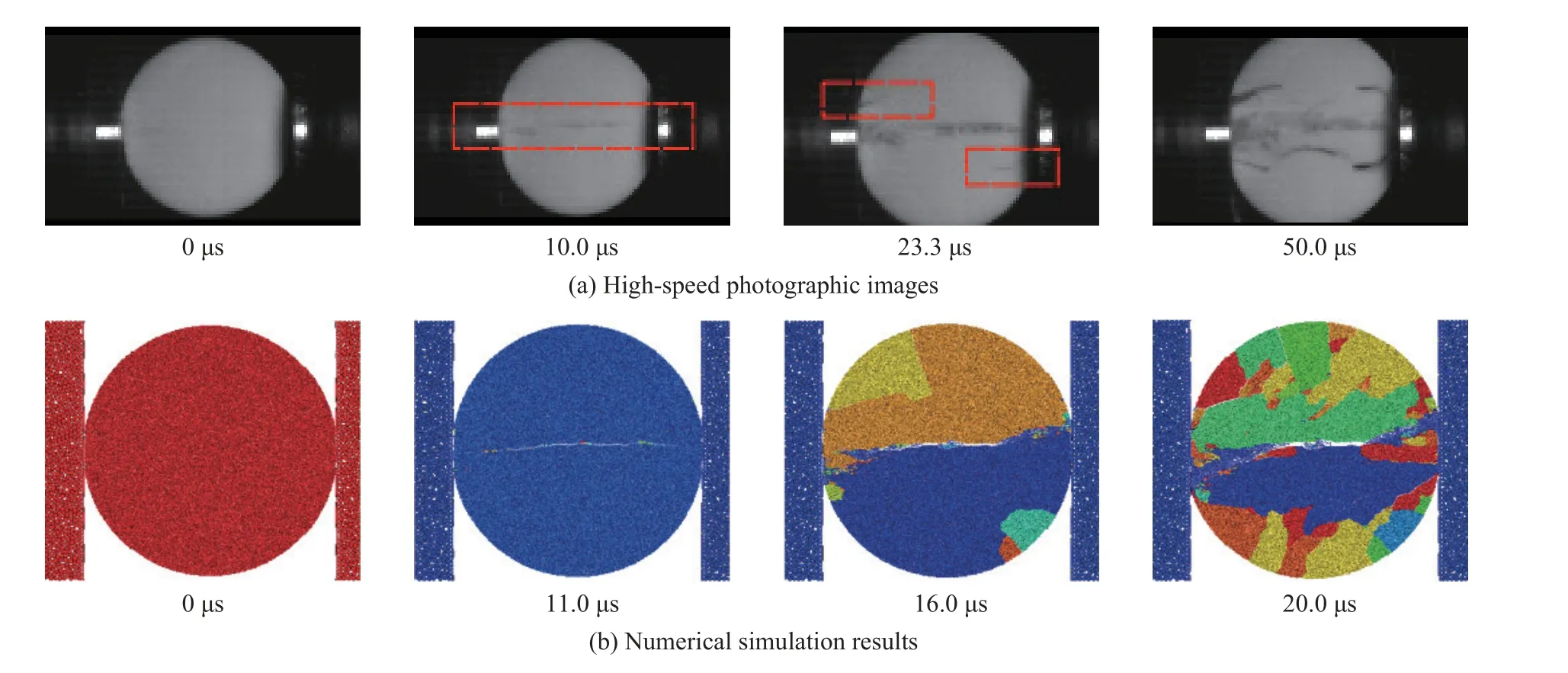
图5 陶瓷试件巴西劈裂的破坏过程Fig.5 Failure process of the ceramic specimen in Brazilian splitting test

3 含预制裂纹平台圆盘的裂纹扩展

3.1 翼型裂纹扩展过程

脆性材料的内部缺陷对其破碎过程有重要影响，对含预制裂纹陶瓷试件的动态破坏特性进行数值模拟，其中陶瓷试件（ ∅14 mm）模型中预制裂纹长度为7 mm，且预制裂纹与水平加载轴线的夹角为β，模型参数及接触模型同2.1 节。

图6 为β=30°时陶瓷试件不同时刻的受力云图。当预制裂纹尖端附近的应力集中区域（红色标注）内应力强度因子达到临界值时，拉伸裂纹成核，试件产生新裂纹，该处应力强度因子降低；继续加载后，新裂纹尖端处应力强度因子增大，再次萌生新裂纹并扩展；t=90.8 μs 时，由于入射波及反射波到达预制裂纹两端裂尖的先后顺序不同，预制裂纹两个尖端处新裂纹萌生扩展并不同步；t=94.0 μs 时，试件边缘处产生应力集中（红色标注），次生裂纹开始萌生。

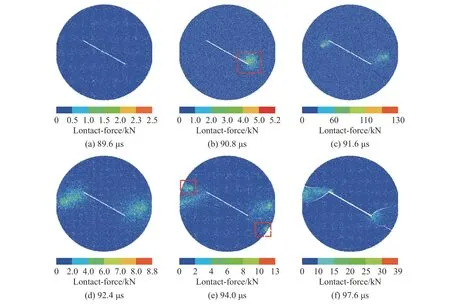
图6 β=30°时含预制裂纹陶瓷不同时刻的受力云图Fig.6 Stress distribution of the ceramic specimens at different moment with prefabricated cracks at β =30°

图7 给出了β 分别为0°、15°、30°、45°、60°时陶瓷试件的裂纹演化过程。冲击载荷下陶瓷试件具有以下拉伸破坏特点：(1) 加载初期（t=92.4 μs），新生裂纹从预制裂纹尖端处成核萌发，向加载端生长。(2)t=97.6 μs 时，载荷增加，裂纹稳定扩展，主裂纹贯穿试件的同时，次生裂纹在圆盘试件的边缘处生成并扩展；当轴向载荷到达峰值后（t=101.6 μs），大量裂纹成核、扩展并汇合，导致试件完全破坏；(3) 当β=0°时，主裂纹扩展为一条直线，其余工况下主裂纹均为翼型裂纹，且裂纹扩展方向最终与水平加载轴线方向平行，该计算结果与实验[19]得到的宏观破坏模式一致。

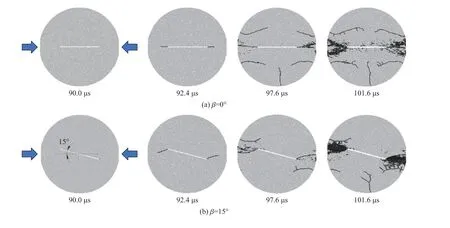
图7 不同β 下陶瓷的裂纹演化过程Fig.7 Crack evolution process of the ceramic specimens with different β

3.2 翼型裂纹起裂分析

含预制裂纹的试件中，新裂纹的产生与预制裂纹尖端处所受的复杂应力状态相关。加载的应力波在试件内会发生多次反射和透射，试件将承受剪应力与拉应力的共同作用，导致裂尖处形成翼型裂纹，如图8 所示，其中：2c 为陶瓷样品的预制裂纹长度。翼型裂纹模型被广泛用于描述压缩载荷下脆性材料内的裂纹扩展[20–21]，为此，本研究采用该模型描述裂纹扩展，如图9 所示，其中：θ 为起裂角。压缩加载下，随着载荷的增加，当作用在预制裂纹上的局部剪应力逐渐克服摩擦极限时，裂纹面将产生相对滑移，如图9(a)所示；当裂纹尖端处应力集中导致的应力强度因子达到裂纹扩展准则（如双K 断裂准则）时，尖端处沿θ 方向产生翼型拉伸裂纹（即阴影部分）；随着拉伸裂纹的扩展，拉伸裂纹最终与主压缩应力平行。

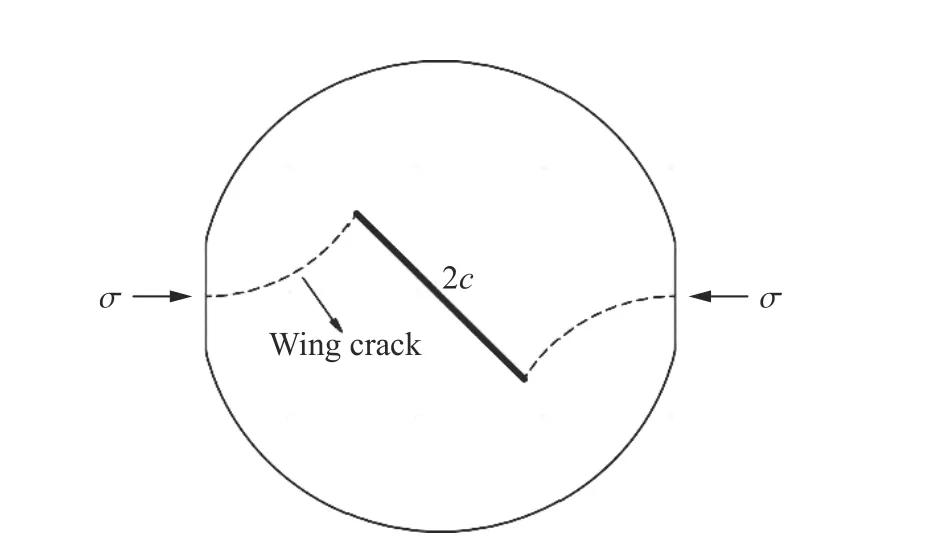
图8 翼型裂纹示意图Fig.8 Schematic diagram of wing crack

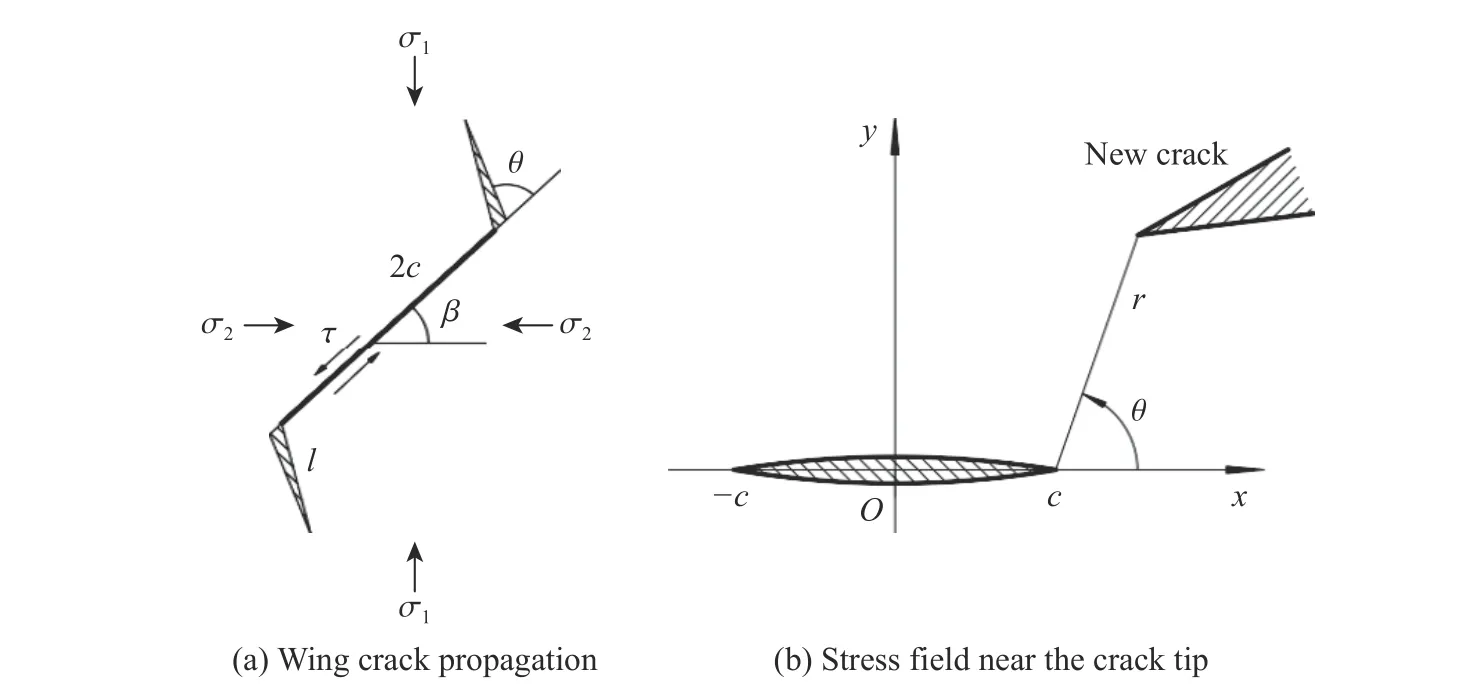
图9 翼型裂纹模型Fig.9 Model of wing cracks

如图9(b)所示，基于Ⅰ型和Ⅱ型裂纹尖端的应力场分布[22]，对于平面问题，Ⅰ-Ⅱ型复合裂纹尖端附近应力场的极坐标表达式为

根据最大拉应力原则，裂纹的扩展方向为周向应力 σθ取最大值的方向，且当周向应力 σθ达到临界值 σc时，产生新裂纹，此时

将式（2）代入式（1）可得

若起裂时的应力强度因子已知，可根据式（4）预测在不同倾角下试件的起裂角度。纯Ⅱ型裂纹扩展时（KⅠ=0，KⅡ≠0），式（4）可以转化为3cosθ－1=0，计算可得起裂角为70.5° ；纯Ⅰ型裂纹扩展时，由sin θ=0 得到起裂角为0°。

求解式（4）可得

将θ0代入 ∂2σθ/∂θ2，当满足 ∂2σθ/∂θ2<0时，对应的θ0即为有效解。董世明等[23]在无裂纹圆盘的应力分量解析解基础上，用权函数方法推导出中心裂纹圆盘试件应力强度因子KⅠ和KⅡ的值，将KⅡ/KⅠ代入式（5），得到起裂角的理论预测值，见表3 和图10。可以看出，预制裂纹倾角在0° ～ 60° 时，起裂角随倾角的增大而增大。当倾角在0°～20° 时，起裂角逐渐增大并趋于70.5°；倾角从20° 增大到25°时，起裂角从68.0°增大到111.1°，增幅较大。此外，根据式（5）计算可得，起裂角的取值区间不包括 [70.5°，109.5°]。如图10 所示，起裂角的数值模拟结果与理论预测值吻合度良好。研究表明，不同倾角的预制裂纹圆盘试件在承受冲击载荷时，会产生介于Ⅰ型与Ⅱ型裂纹之间的复合型裂纹。图11 显示了倾角β=60° 时翼型裂纹扩展路径和裂纹两侧的粒子位移场分布。翼型拉伸裂纹在预制裂纹尖端起裂后进一步扩展，并最终与圆盘试件的中心水平轴线平行（图11(a)）。结合前面起裂角随倾角变化的规律可知，初始新裂纹尖端成核时会产生Ⅰ-Ⅱ型复合裂纹，当翼型裂纹的尖端逐渐扩展至M点时，MO与加载方向轴线的夹角减小，新裂纹的起裂角也随之减小。当裂纹逐渐扩展至加载轴线时，复合裂纹逐渐转化为Ⅰ型裂纹（KⅡ=0），新裂纹的起裂角趋于0°。

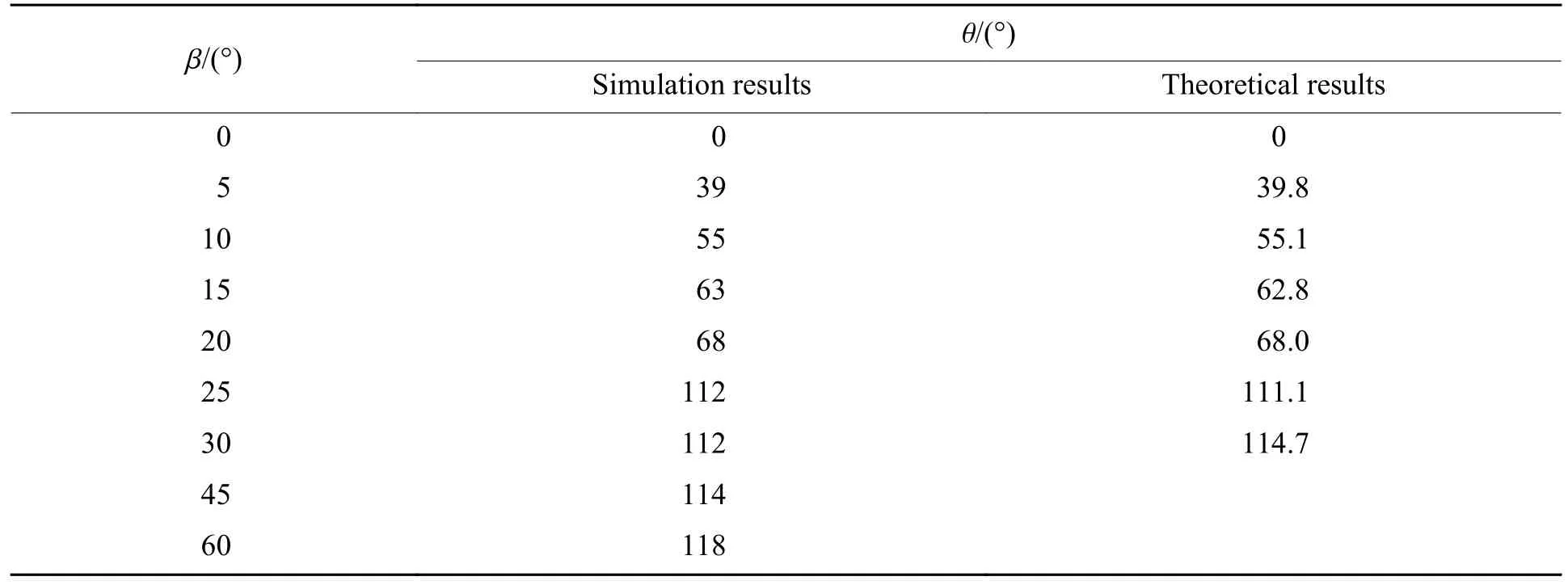
表3 理论和数值计算的起裂角对比Table 3 Comparison of the crack initiation angles between theoretical and simulation results

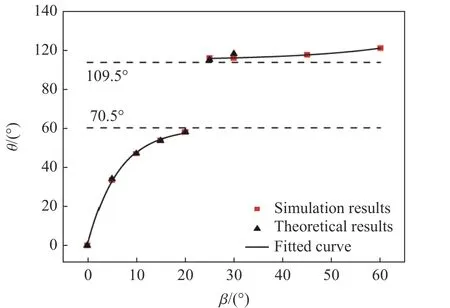
图10 不同倾角β 下的起裂角Fig.10 Crack initiation angle at different β

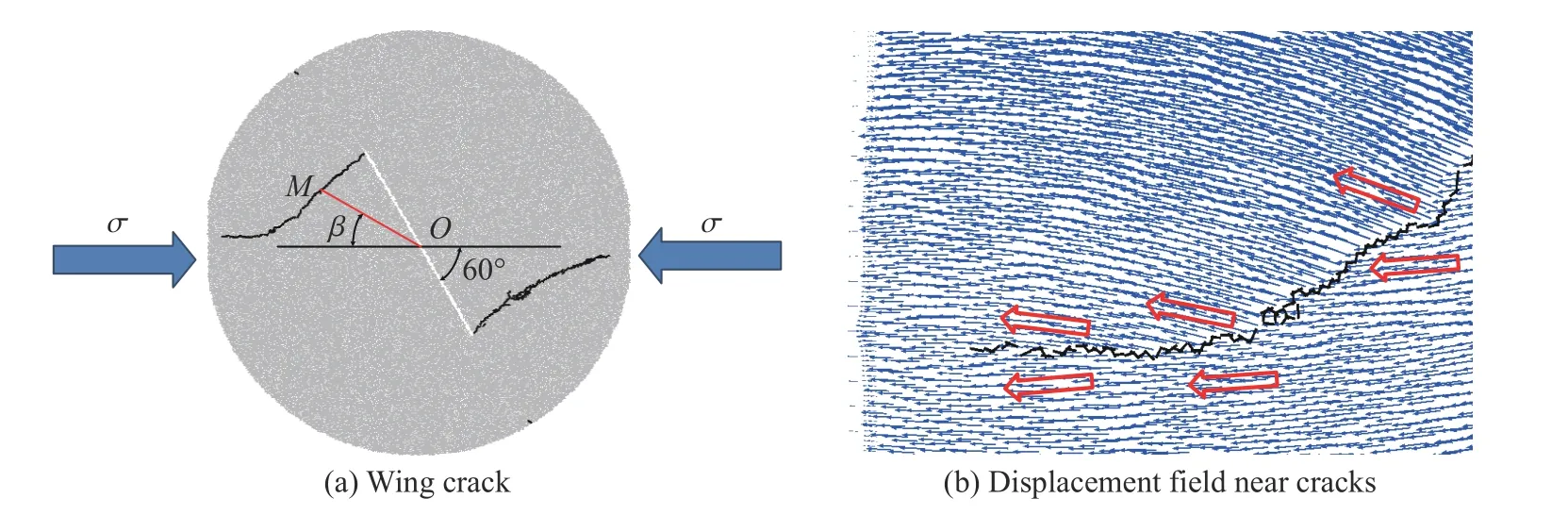
图11 β=60°时裂纹的演化Fig.11 Evolution of cracks at β=60°

在颗粒流计算中，研究两个颗粒间的单一微裂纹是无具体意义的，宏观裂纹是多个颗粒之间形成的微裂纹集。因此，在数值计算中，外部载荷作用下陶瓷内部裂纹成核生长，多个微裂纹汇聚交错使试件发生宏观裂纹，此时试件承受的应力认为是起裂应力。图12 为含预制裂纹试件与加载轴线呈不同倾角时起裂应力的变化规律。随着倾角的增大，起裂应力呈现先减小后增大的变化趋势；当倾角为30°时，起裂应力最小，表明预制裂纹尖端处最容易产生翼型裂纹，文献[24–25]研究了单轴加载下岩石的破坏，也有相类似的结论。

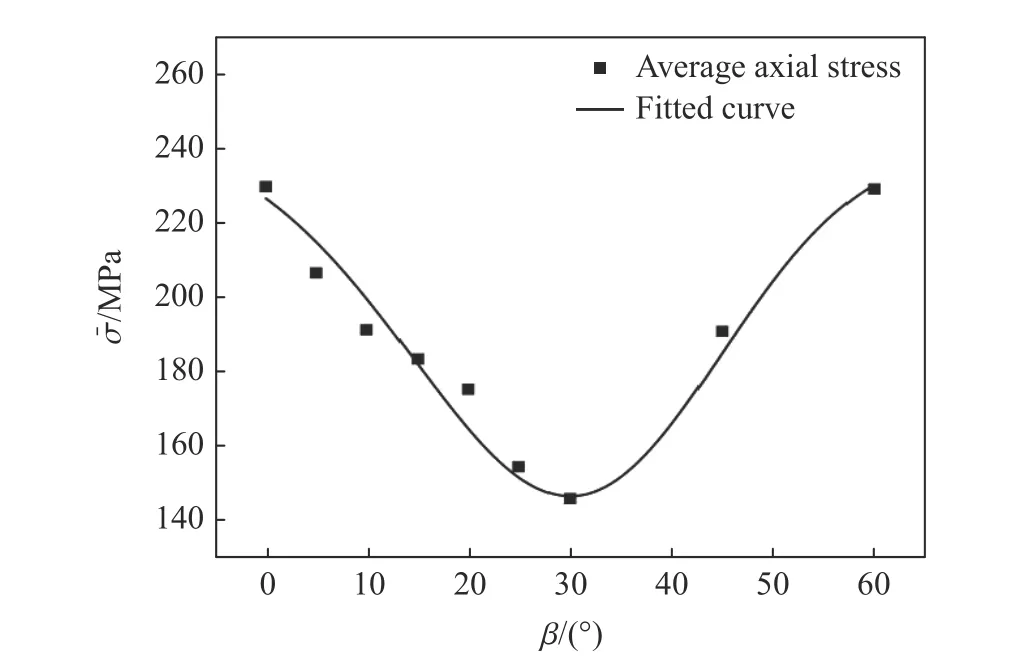
图12 不同倾角β 下的起裂应力Fig.12 Crack initiation stress at different β

4 结 论

本研究基于离散元法和改进的SHPB 实验装置研究了平台圆盘氧化铝陶瓷的动态拉伸破坏，揭示了不同倾角下含预制裂纹平台圆盘试件的裂纹扩展和演化过程，并结合裂纹尖端的应力场分布获得了翼型裂纹的起裂特征。

(1) 基于颗粒流法，建立了基于SHPB 实验技术的数值计算模型，标定了氧化铝陶瓷的平节理黏结模型参数，并结合宏观力学参数验证了数值计算模型的有效性。

(2) 氧化铝陶瓷动态破坏的离散元模拟结果表明，陶瓷试件初始裂纹出现于试件中部，次生裂纹从圆盘边缘处萌发并向试件中部发展，大量裂纹扩展与汇合导致试件最终产生轴向劈裂破坏，与实验现象一致。

(3) 倾角（预制裂纹与加载轴线的夹角）为0°～ 60°时，拉伸破坏为氧化铝陶瓷试件的主要破坏模式。由于预制裂纹尖端处存在应力集中，导致翼型裂纹从预制裂纹尖端处萌生并扩展，最终与加载轴线方向平行。随着倾角增加，起裂角增大，起裂应力呈现先减小后增大的变化趋势；当倾角为30°时，平台圆盘陶瓷试件内最容易产生翼型裂纹。