适当“留白”成就别样精彩

单小燕

［摘  要］ 数学教学既要关注学生知识与技能的培养，又要重視学生思维能力和创新能力的提高. 要想培养学生的思维能力和创新能力，教师切勿大包大揽，应从学生已有认知水平出发，通过有效“留白”为学生提供一个开放的、平等的学习空间，以此让学生通过独立思考和合作探究获得更为广泛的、深刻的数学理解，从而有效地提升“教”与“学”的品质，打造别样精彩课堂.

［关键词］ 留白；初中数学；教学思考；探究

中国书画作品中通过“留白”尽显美之韵味，给观赏者留下一个无限遐想的空间. 数学教学亦是如此，在教学中给学生留一些遐想的空间，让学生通过思考、探索、感悟来体验数学的美，有助于激发学生的数学学习兴趣. 不过，在现实教学中，为了赶时间、赶进度，课堂教学大多以教师讲授为主，留给学生独立思考的时间和空间较少，从而使得数学教学活动机械、消极. 要知道，数学是思维的学科，只有思维参与的数学活动才是有价值的. 当然，“留白”并不是放任自流，若在教学中频繁地“留白”，容易限制学生思维的发展，影响学生学习兴趣的激发，可见“留白”需要教师深思熟虑. 教师要结合教材内容和学生实际精心设计“留白”，从而使课堂教学张弛有度，既能顺应学生的思维发展，又能激发学生的学习积极性.

众所周知，好的课堂并不是让学生被动地接受知识，而是让学生主动地获取知识. 为了调动学生参与的积极性，引导学生主动思考、主动探究、主动获取，教师就不能大包大揽，应为学生创设独立思考的空间. 而课堂教学中的有效“留白”恰好为学生创设了独立思考的空间，其既有助于促进学生的个性化发展，又有助于“和谐、民主、开放”的高效课堂建构. 那么，教师应如何设计“留白”来成就精彩的、高效的课堂呢？

导课中“留白”激兴趣

引入是数学教学的重要一环. 在教学中，教师应结合教学实际精心预设课堂导入内容，从而在教学之初就紧紧吸引学生的注意力，以此促进课堂知识的生成. 值得注意的是，在引入环节教师不应直接将结果展现给学生，而应设计一些悬念，诱发学生思考，以此激发学生的探究欲.

1. 备课“留白”，预设探究空间

教师在备课时不仅要备教材，还要备学生，知晓学生的“最近发展区”，只有这样才能设计有效“留白”，引导学生发现问题并提出问题. 不过，在教学中，大多数教师喜欢包办代替，这样学生的思路被教师牵着走，难以真正地参与课堂. 为了改变这一现象，教师在备课时不妨尝试运用“留白”，将一些提出问题的机会留给学生，引导学生主动发现问题并自主探究，寻求解决问题的不同方法，让学生在提出问题、分析问题和解决问题的过程中感知、顿悟. 当然，教师要对学生可能提出的问题进行大体预测，并设计一些应对策略，以确保教学计划顺利实施，教学目标顺利实现.

2. 导入“留白”，激发探究热情

在数学教学过程中，教师要知道哪些内容该讲，哪些内容可以留着不讲. 不讲的内容不是说它不重要，而是该部分内容符合学生的认知，可以通过启发和指导让学生自己发现、提出并解决. 因此，在引入新知环节，教师应该设计一些悬念，利用一些既“够得着”又必须“跳一跳”的问题来激发学生的探究欲，促进学生主动学习.

例1  “一元一次不等式”新知引入.

问题情境：某市篮球联赛的票价为20元/人，若满20人以上（含20人）可以购买团体票，团体票享八折优惠. 现有18人去观看比赛，请问需要准备多少钱？

生1：360元. （该生不假思索地回答）

师：很好，生1是如何购票的？

生（齐）：按照零售价购票，20×18=360（元）.

师：还有没有花费更少的购票方案呢？

生2：可以按照团购方案购买，购买20张门票只需320元，比按照零售价购买更划算.

师：非常好，真是有“比较”才有最优，“比较”就是我们本节课的核心词汇.

导入留白 若x名学生购买团体票（x<20），当x满足什么条件时买20张门票反而花更少的钱呢？你能利用不等式求解吗？

生3：20x>20×20×0.8.

师：如何解呢？

设计意图  从学生熟悉的购票情境出发，借助“买更多花更少”引发认知冲突，给学生创设思考的空间，引导学生利用不等式模型解决生活问题.

初中生已具有一定的分析和解决问题的能力，教师要相信学生，为学生提供一定的探究空间，鼓励他们主动寻找解决问题的方案，以此激发学生的潜能，培养学生的数学学习信心. 如在本案例的教学中，教师先是从学生认知出发，发现有时多买反而更省钱，从而引发认知冲突，让学生在解决冲突的过程中通过自主探索获得不等式模型，由此引出本课的主题. 以上教学过程既顺应了学生思维的发展，又有效地激发了学生的求知欲，有助于教学效率的提升.

探知中“留白”促生成

在学习中，学生要通过自主探究经历知识的形成过程，从而获得对数学知识的理解，完善个体认知结构. 不过学生认知结构形成的过程是曲折的，此过程离不开教师的启发和指导. 为了更好地启发学生自主探究，教师可以在问题的关键点处“留白”，这样不仅可以唤起学生的探究欲，而且可以直指数学本质，让学生更加深入地理解数学知识，建立正确的认知.

1. 问题生成处“留白”，激发探究欲

问题在诱发学生思考、激发学生潜能、提升学生探究欲、提高学生学习能力等方面具有重要的价值. 不过在实践教学中发现，大多数教师觉得课堂时间宝贵，为了避免学生走弯路，或不想让学生的突发奇想打乱教学预设，教师在提出问题后并没有给足学生思考的时间就急着让学生回答或自问自答，这样不仅削弱了问题的思考价值，而且影响了学生学习能力的提升. 因此，教师在提问后应适当停顿，为学生提供一定的思考空间，为学生创设一个自由展示的舞台，以此充分暴露学生的思维过程. 且通过互动交流，学生既可以更好地认识自己，又可以感知他人的想法，从而提高发现问题、提出问题和解决问题的能力，并获得更深层次的顿悟，认清问题的本质.

例2  某水果超市以2.5元/千克的价格购进一批苹果，并在进价的基础上提价20%出售.

（1）该超市苹果的售价为_____元/千克；

（2）每卖出1千克苹果可以获利_____元；

（3）该超市销售苹果的利润率是______.

试题给出后教师并没有让学生急于寻求答案，而是让学生思考如下问题：

问题1：分别写出商品的进价、售价、利润，思考如何计算商品的利润率.

问题2：为了加快销售速度，防止因苹果腐烂而造成损失，该超市决定按售价的八折出售，此时苹果的售价是多少？

问题3：超市开始在进货价的基础上提价20%出售，后面受季节等因素的影响按照售价的八折出售，那么该超市出售该商品是否获利了？

以上是教师在教学“一元一次方程应用”时精心设计的一道探究题，旨在通过由易到难、由旧推新、由具体到抽象的问题来引发学生进行数学思考，让学生始终处于积极的、主动的探索氛围之中，从而提升教学效率.

2. 重难点处“留白”，展示思维过程

在初中数学教学中，许多教师经常有这样的困惑：对于一些重难点知识，教师反复强调，学生反复练习，但是学生在解题时依然是“一错再错”. 是什么原因造成了这一现象呢？其主要原因是学生在学习的过程中缺少独立思考的过程，从而出现了“懂而不会”的现象. 其实，教师在讲解重难点内容时，有时候不需要特意强调，更不需要越俎代庖，可以故意保留一些内容，让学生自己去思考、去探索、去感悟，允许学生犯错，并让学生在错中反思、顿悟，深化对知识的理解.

例3  图1为一个长20米、宽12米的草地，草地内有一条宽1.5米的小路，你能求出草地的实际种植面积吗？说一说你的理由.

例3主要考查学生对平移变换的理解，在之前的教学中，教师尝试通过“反复讲”来帮助学生理解，效果一般. 受思维定式的影响，学生在计算种植面积时习惯用总面积减去阴影面积，但对于这条曲折的小路，很难直接计算出其面积，所以很多学生在解决本题时束手无策，可见学生并没有真正理解平移变换的本质. 为了帮助学生主动探索并突破这一难点，教师借助变式让学生顿悟.

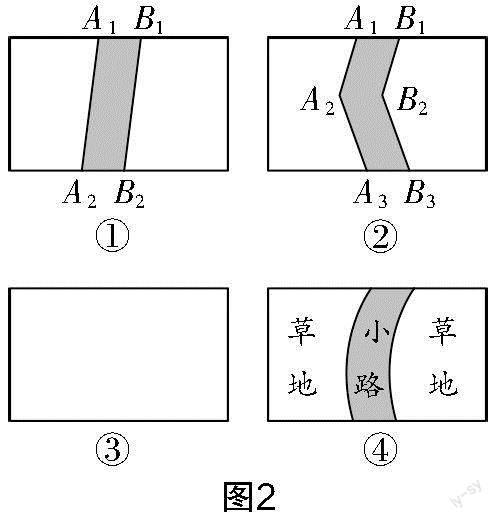
变式问题：如图2①所示，将线段AA向右平移1个单位长度得到BB，得到封闭图形AABB（阴影部分）；如圖2②所示，将折线AAA向右平移1个单位长度得到BBB，得到封闭图形AAABBB（阴影部分）.

（1）请在图2③中画一条有2个折点的折线，将其向右平移1个单位长度，画出封闭图形，并用阴影表示.

（2）设图2中4个长方形的长均为a、宽均为b，你能求出各图形的面积吗？（阴影部分除外，图④中小路的宽为1）

借助变式，将问题进行整合，能让学生从整体的角度去思考和解决问题，这样不仅有利于学生突破教学重难点，而且能让学生通过自主探究发现蕴含其中的规律.

在实际教学中，教师应该创设一些有思考价值的问题诱发学生思考，让学生站在更高的角度理解问题，切勿通过“填鸭”式教学剥夺学生思考的权利. 教师要善于借助有效“留白”激发学生的探究欲，以此突破教学重难点.

3. 思维障碍处“留白”，突破思维局限

因个人认知水平、思维习惯等方面存在差异，学生思考问题和解决问题的方法也会存在差异. 在教学中教师要合理利用个体差异，让不同思维在争论中碰撞出火花，进而丰富学生的认知，弥合个体思维的缺陷，点燃学生学习数学的热情，让学生逐渐建构个体完善的认知. 为了达到以上教学效果，教师可以在某个问题的焦点处“留白”，为学生提供时间和空间去争论，让学生在争论中使思维完整.

例4  如图3所示，两抛物线关于y轴对称. 若AB∥x轴，AB=4 cm，最低点C在x轴上，高CH=1 cm，BD=2 cm，则抛物线DFE的函数解析式为（     ）

从学生的课堂反馈来看，该题的正确率不高. 分析原因发现，有的学生是想直接根据已知求抛物线DFE的函数解析式，但是因为已知条件不足而未能顺利求解；有的学生先求抛物线ACB的函数解析式，然后运用轴对称解决问题，但是因为没有准确求出抛物线ACB的函数解析式而造成错误；有的学生准确地求出了抛物线ACB的函数解析式，但是在求抛物线DFE的函数解析式时思维受阻最终没有顺利求解. 学生通过互动交流可以解决上述问题，为此教师将探究的主动权交给学生，鼓励学生通过争论突破难点.

师：与其他同学交流一下你的解题过程，思考一下自己的错误出在哪里，应该如何求解.

生1：若想求抛物线DFE的函数解析式，需要知道D，E，F三点的坐标，根据已知无法直接求出，但抛物线ACB和抛物线DFE关于y轴对称，这样根据轴对称性质，先求得A，B，C三点的坐标，即可得到D，E，F三点的坐标. 不过，在解题时我忽略了抛物线ACB的作用，一味地在抛物线DFE中挣扎，所以没有找到解题的突破口，最终“走投无路”.

生2：还可以先求出抛物线ACB的函数解析式，然后根据轴对称求抛物线DFE的函数解析式. 我在解题时因为运算马虎，得到了错误的抛物线ACB函数解析式，从而导致结果错误.

师：很好，从以上两种解法可以看出，本题若想求解少不了利用轴对称的性质.

师：求抛物线解析式时，你用的是什么方法？

生3：三点法，求出D，E，F三点的坐标，利用解方程组的思路求解.

生4：两根式，结合图象可知抛物线的顶点在x轴上.

生5：顶点式，根据选项容易发现其最终的结果为顶点式，这样就不需要后期再进行转化了，有助于提高解题效率.

通过平等的交流、争论，学生找到了适合自己的最优解决方案，此时教师已经没有再进行讲评的必要了. 可见，在讲评错题时，给学生一定的时间和空间去回顾、思考、交流，往往可以收获得更多. 思辨“留白”，能让不同思维相互碰撞. 学生通过相互学习，不仅纠正了错误，而且发现了解决问题的不同策略，他们在争论和辨析中完善和升华了自身的思维.

总之，教师要认真研究教材、研究学生、研究教学，巧妙地应用“留白”让学生有所思、有所悟、有所获，以此让学生的思维向着更广阔、更灵活、更深刻的层次发展，从而有效地提高学生的学习品质，打造精彩的数学课堂.