吃透基本图形对提升学生数学学力的研究

杨丽萍

［摘  要］ 平面几何中的基本图形是指几何问题中常见的、具有典型特征，能够得到常用结论的一些图形. 基本图形的掌握，有助于提高学生的几何直观和想象能力，再通过猜测、验证、发现结论，能从某种程度上有效促进学生几何思维的发展.

［关键词］ 基本图形；数学教学；数学学力.

《义务教育数学课程标准（2022年版）》指出，数学源于对现实世界的抽象，我们在学数學的过程中，可以通过对数量和数量关系、图形和图形关系的抽象、提炼，得到新的研究对象具备的结论或关系. 教师的教育教学应注重对基础知识、基本技能的教学，并督促学生理解基础知识、掌握基本技能. 掌握“知识与技能”是学生发展的最基础目标，同时要落实“数学思考”“问题解决”“情感态度”等目标. 在教学中，教师应注重学生对所学知识的理解与掌握，让学生体会数学知识之间的关联，实现数学知识真正意义上的内化. 当然，学生掌握数学知识，绝对不能依赖死记硬背，而应在理解的基础上应用知识，并不断巩固、深化、内化知识. 笔者认为，根据课程标准的指导意见，教师在教学中，应注重培养学生的数学学力，使学生进一步领悟数学核心素养（数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析）. 数学学力与数学核心素养之间并不是相互独立的，二者相辅相成. 数学核心素养对数学教学具有明确的指导意义，起着统领性的作用. 数学学力则可以看作是在核心素养指导下数学学习中较为实用的具体操作方法，它是数学核心素养的现实操作路径，具有可操作性、具体化的特点.

学生都想学好数学这门课，但无奈自身数学学力的缺乏，使得绝大部分学生学得非常吃力. 笔者也经常听到身边的同事这样吐槽：“这道题我都讲了无数遍了，怎么还有这么多人做不对？”从这句话中可以得到两个信息：一，这道题经常考，在平时的练习中出现的频次较高，姑且说它是典型题；二，学生的学习效率不高，一个高频出现的练习题，学生多次接触后仍有部分做不对. 基于这两点，笔者深刻地体会到，在平时的教学中教师应采取措施去提升、发展学生的数学学力. 数学家波利亚曾经主张：与其做大量的难题，不如把一道题的各个侧面研究通透，这样会积累更好的经验，提高解决其他问题的能力. 基于波利亚的主张，教师在教学中应深挖问题本源. 平面几何问题的本源是一些基本图形，具体指几何问题中常见的、具有典型特征，能够得到常用结论的一些图形. 基于某一类基本图形的变式题或拓展题比比皆是，学生只要熟练掌握基本图形，经历猜测、验证、发现结论的过程，便能求解. 在求解的过程中，学生提高了几何直观和想象能力，发展了数学思维，对提升数学学力起到了立竿见影的效果. 下面以基本图形“飞镖形”在解题中的灵活应用为例，进行具体阐述.

基本图形——“飞镖形”

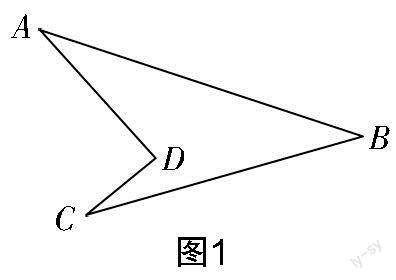
如图1所示的凹四边形称为“飞镖形”，在“飞镖形”图形中，∠ADC与∠A，∠C，∠B之间的数量关系为∠ADC=∠A+∠C+∠B. 该数量关系可以通过添加辅助线（连接BD并延长），并利用三角形的外角性质得到.

试题1  一个五角星如图2所示，则∠A+∠B+∠C+∠D+∠E=_____.

对于此题，有些学生无从下手，但是仔细观察图形，不难发现该图形中含有基本图形“飞镖形”，利用“飞镖形”的重要结论，再结合三角形的外角性质，很容易得到该题的答案为180°.

试题2  如图3所示，P是△ABC三个内角平分线的交点，O是△ABC三边垂直平分线的交点. 若∠BPC=115°，则∠BOC=______.

∠OCA+∠BAC=∠OAB+∠OAC+∠BAC=∠BAC+∠BAC=2∠BAC=100°.

以上两题的解决，说明了在复杂图形中提炼出基本图形的重要性. 所以教师在教学中一定要引导和帮助学生提炼出基本图形，并要求学生记住基本图形相应的结论.

变式1  在四边形ABCD中，∠A=x，∠C=y.

（1）∠ABC+∠ADC=______（用含有x，y的代数式表示）.

（2）如图5所示，BE，DF分别为∠ABC的外角平分线和∠ADC的外角平分线.

①若BE∥DF，x=30°，则y=______；

②当y=2x时，若BE与DF交于点P，且∠DPB=20°，求y的值.

（3）如图6所示，∠ABC的平分线与∠ADC的外角平分线交于点Q，则∠Q=______（用含有x，y的代数式表示）.

第（1）题比较简单，利用四边形的内角和为360°就可以得到∠ABC+∠ADC=360°-x-y.

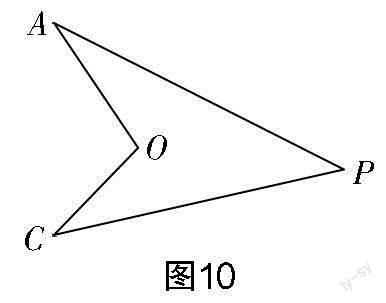
变式2  我们将图10所示的凹四边形称为“飞镖形”. 在“飞镖形”中，我们很容易得到∠AOC与∠A，∠C，∠P存在数量关系∠AOC=∠A+∠C+∠P.

利用“飞镖形”模型解决下列问题：

（1）如图11所示，若AP平分∠BAD，CP平分∠BCD，∠B=28°，∠D=48°，求∠P的大小；

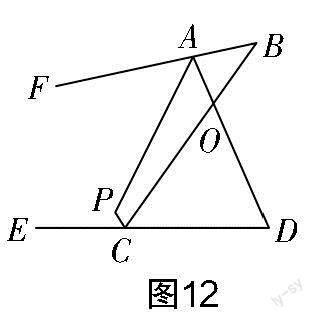
（2）如图12所示，已知直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B，∠D的关系，并说明理由；

（3）如图13所示，已知直线AP平分∠BAD，CP平分∠BCD的外角∠BCE，则∠P与∠B，∠D的关系为______.

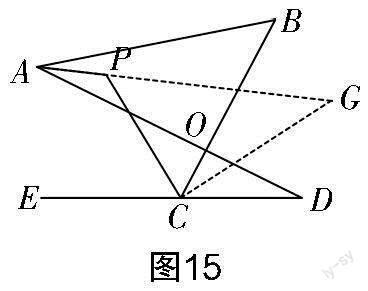
对于第（3）题，有了第（2）题的解题经验，该题不难想到辅助线：作∠DCO的平分线交AP的延长线于点G（如图15所示）. 图15中仍含有两个

解后反思

上面2道变式题都是测试中的压轴题，在学生看来，无疑难度非常大. 一部分有畏难情绪的学生，光看题目中复杂的图形就望而却步了. 而我们在解决上面两道“难题”时 ，能从复杂图形中找到熟悉的基本图形──“飞镖形”，在难度层层递进的梯度问题解决中，运用了类比、追本溯源的方法，从而轻松、灵活地解决了“难题”.  以研究平面图形为主的初中几何，随着所学知识的增多、内容的加深，一些几何题的综合性和复杂性也不断增加，学生在解题过程中需要养成良好的数学图形观察习惯，要将复杂图形转化或者类比为常见的基本图形. 在教学中，对于复杂题型、图形，教师要善于引导学生进行去复杂化，转化、提炼出基本图形或转化成熟悉的知识去解决. 长此以往地训练，必然有利于学生数学学力的培养与提升. “基本图形”只是初中数学几何中的一小部分，通过吃透“基本图形”来提升数学学力的措施也启发我们，可以从与学生联系比较密切的典型题型出发，通过学生对于典型题型的理解与吃透来让学生积累解题经验，形成“模式”. 这样，在学生面对稍难或一些变式题型时，就可以透过现象看本质，通过类比，洞察解题规律与本质，从而在解题时达到事半功倍的效果.