高墩大跨连续梁桥内力位移双控减隔震体系的有效性初探
唐文乐,张俊平,谢柱坚,苏建旭,王 波
(广州大学 工程抗震研究中心,广州 510006)
减隔震技术应用于桥梁工程已经超过30多年,减隔震设计逐渐成为一种有效的地震响应控制方法[1]。连续梁是一种常见的、经济的桥型,但如何将减隔震技术运用于高烈度区高墩大跨连续梁桥的设计中,目前仍存在一些问题,主要表现为墩底内力与梁端位移有效控制的矛盾。大跨度连续梁的隔震设计通常采用铅芯橡胶支座或摩擦摆支座,在有效削减墩底内力的同时,会增大梁端的位移[2-3]。另一方面,随着跨径的增大,梁体自身的惯性力迅速增大,地震作用下梁端位移会进一步放大,这对于柔性高墩大跨连续梁桥尤为突出[4-5]。过大的梁体位移不利于伸缩缝的设计,会导致梁体碰撞、落梁等问题发生。
在国内外,有一些使用黏滞阻尼器和隔震支座组合来控制高墩大跨连续梁的墩底弯矩和梁端位移的工程实践。如在智利修建的Amolanas大桥桥墩高达99.6 m,采用摩擦滑动支座和两侧桥台处设置黏滞阻尼器的组合方案,取得了较好的减震效果[6];美国加利福尼亚州南部91/5公路立交桥经过综合比较分析,表明组合使用橡胶支座和黏滞阻尼器是该桥的最优减震方案[7];Li等[8]以一等截面变高墩大跨连续梁为工程背景,搭配使用铅芯橡胶支座和黏滞阻尼器能使纵桥向各桥墩的滞回能力消耗趋于平均,较好地控制高墩地震反应;鲁传安等[9]采用双曲面球型隔震支座和黏滞阻尼器对墩高为51 m和31 m的3跨连续梁进行减隔震设计,使各墩位移趋于一致,与原结构相比纵向位移最高减小了70%。以上案例均说明在高墩大跨连续梁桥的抗震设计中,组合使用隔震支座和黏滞阻尼器可一定程度的实现墩底内力-梁端位移双控的效果。但是,黏滞阻尼器加工要求较高、可靠性较差等缺陷一直未得到完全解决,漏油等密封问题仍然困扰着工程界。如在2022年9月5日四川泸定6.8级地震震后调查中发现,泸定县燕子沟镇某建筑所使用的黏滞阻尼器出现剪切破坏,连接节点完全拔出[10]。
撑架是连续梁桥顶推施工和悬臂浇筑施工常用的装置。当顶推施工时,将撑架安装在桥墩顶部,可以有效削减梁体负弯矩、减小临时墩的数量;悬臂浇筑施工时,通常利用撑架立模现浇0#块,并作为挂篮施工的临时工作台。但其作为临时结构,在梁体合龙后多拆除。为物尽其用,一些工程采取永临结合的方式,将其作为永久结构的一部分,以减少施工工序、削减支点的负弯矩峰值,如我国1976年采用顶推法施工的东莞市万江大桥,就是一座撑架式混凝土连续梁桥[11]。撑架式连续梁可以有效地减小梁体跨径和内力峰值,但撑架的防撞性能、美观性较差,随着技术的进步,逐渐淡出了工程界的视野。
基于上述分析,本文基于撑架式连续梁桥结构特点和耗能减震的思想,提出一种采用低屈服软钢材料制备撑架、并与摩擦摆隔震支座组合的减隔震体系。首先推导了撑架结构等效阻尼比的计算公式,然后通过Midas/Civil平台,基于阻尼比公式对比研究了4种减隔震方案的地震响应,并对撑架结构进行了参数分析。最后,对附加撑架结构的连续梁进行静力性能分析,探讨了撑架和摩擦摆支座组合以实现高墩大跨连续梁桥墩底内力和梁端位移双控的有效性,为高墩大跨连续梁桥的防震设计提供一种新方法和思路。
1 撑架的等效阻尼比
从施工角度确定撑架尺寸、构造,然后研究其动力行为。撑架的简化计算图式同图1所示。图1中:V为撑架承受的剪力;l为撑架等效为一个斜撑的撑架长度;a为位移角;θ为撑架等效为一个斜撑的支撑角度。撑架的设计原理与耗能减震装置类似,本构模型可采用如图2双线性模型。基于能量等效的原则,在一个振动循环内令等效黏性阻尼比做的功等于实际阻尼做的功,可得到撑架的等效阻尼比ξe
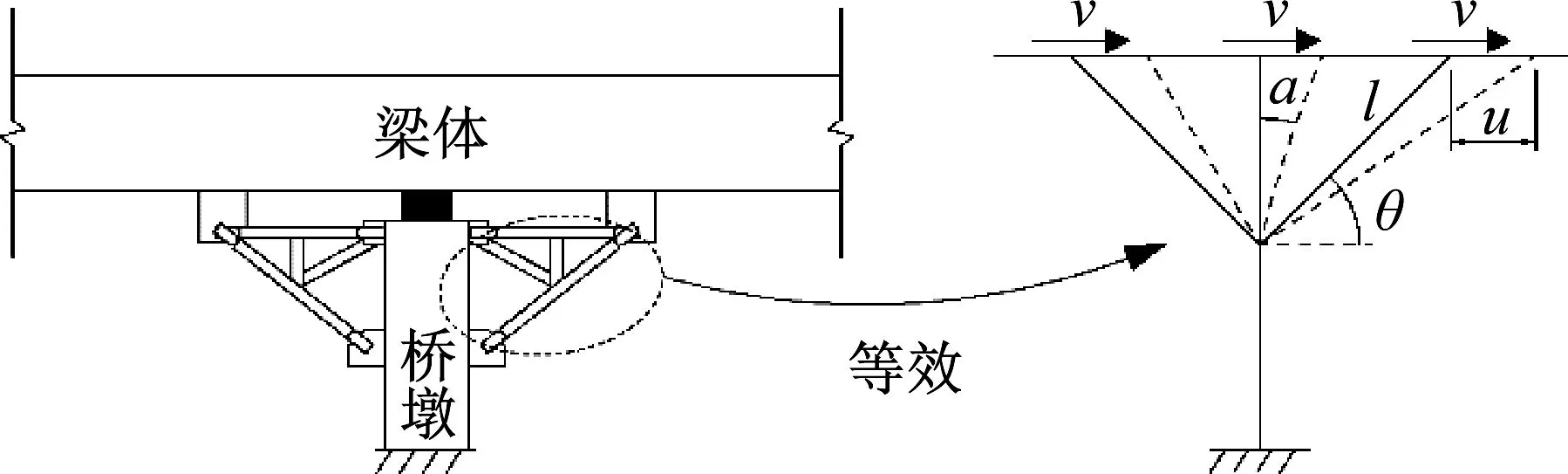
图1 撑架计算简图
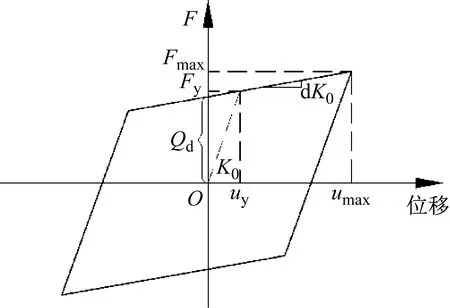
图2 撑架等效阻尼比
(1)
式中:ED为实际阻尼在一个循环内做的功,表示为滞回圈的面积;Ec为结构对应于最大位移的应变能,表示为滞回曲线上的最大位移点与原点连线向位移轴投影得到的三角形面积。等效阻尼比可进一步写为
(2)
式中:Qd为特征强度,即滞回曲线正向与剪力轴相交值;umax为最大位移;Fmax为umax对应的最大力;uy为屈服位移;Fy为uy对应的屈服力;K0为初始刚度;d为刚度因子,取值为0.02。对撑架进行简化分析,则有
(3)
umax=alsinθ
(4)
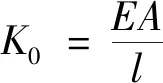
(5)
Fy=K0uy
(6)
式中:E为材料的弹性模量;σy为材料的屈服强度;A为撑架等效截面面积。将式(3)~式(5)和式(6)代入式(2),整理得
(7)
根据等效阻尼比公式式(7)可知,支撑角度θ影响不大,从施工角度分析,可设计为45°,方便其组成构件的设计。a类似于框架结构的层间位移角,参照相关规范可取最大值1/50[12]。在采用Q160LY软钢材料的情况下,依据相关工程经验,确定撑架的等效阻尼比为8%~12%,由此可确定撑架长度和等效截面面积的合理区间,如图3所示。
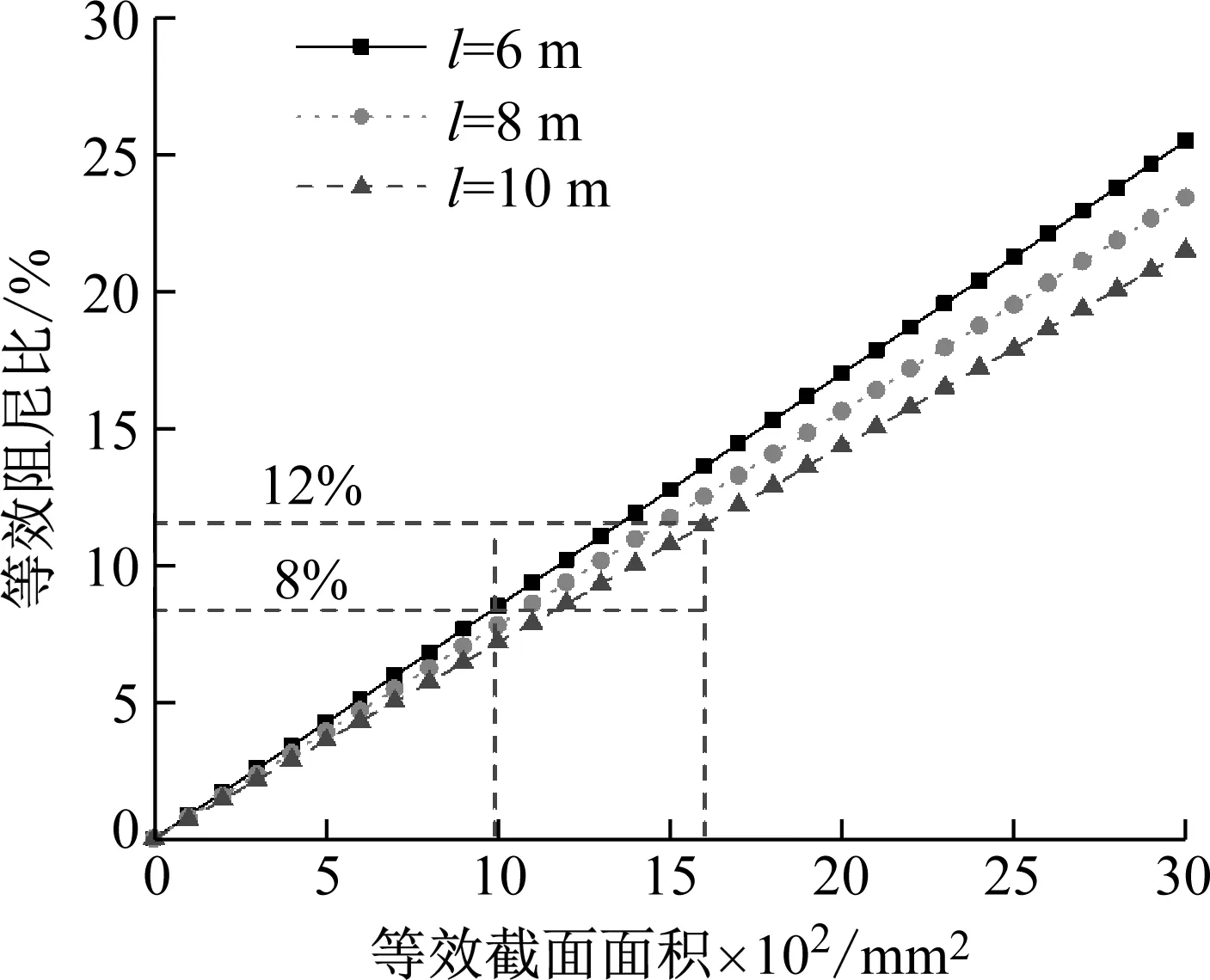
图3 撑架等效阻尼比参数分析
2 减隔震方案比选
采用跨径布置为(54+90+54)m的典型3跨连续梁,梁体为变高度单箱双室箱形截面,箱梁顶宽17 m,箱梁底宽12 m,墩顶梁高5.2 m,跨中及边墩墩顶梁高2.5 m,边墩高20 m,中墩高40 m,采用有限元软件Midas/Civil建立的全桥模型如图4所示。作为初步研究,本文主要探讨该体系的有效性,为此,利用现有的强震记录,选取El-Centro波、Taft波和Northridge波3条地震动数据,使其覆盖连续梁的前几阶频率(1阶频率0.53 Hz,2阶频率1.08 Hz,3阶频率1.13 Hz),对结构进行地震响应时程分析,如图5和图6所示。
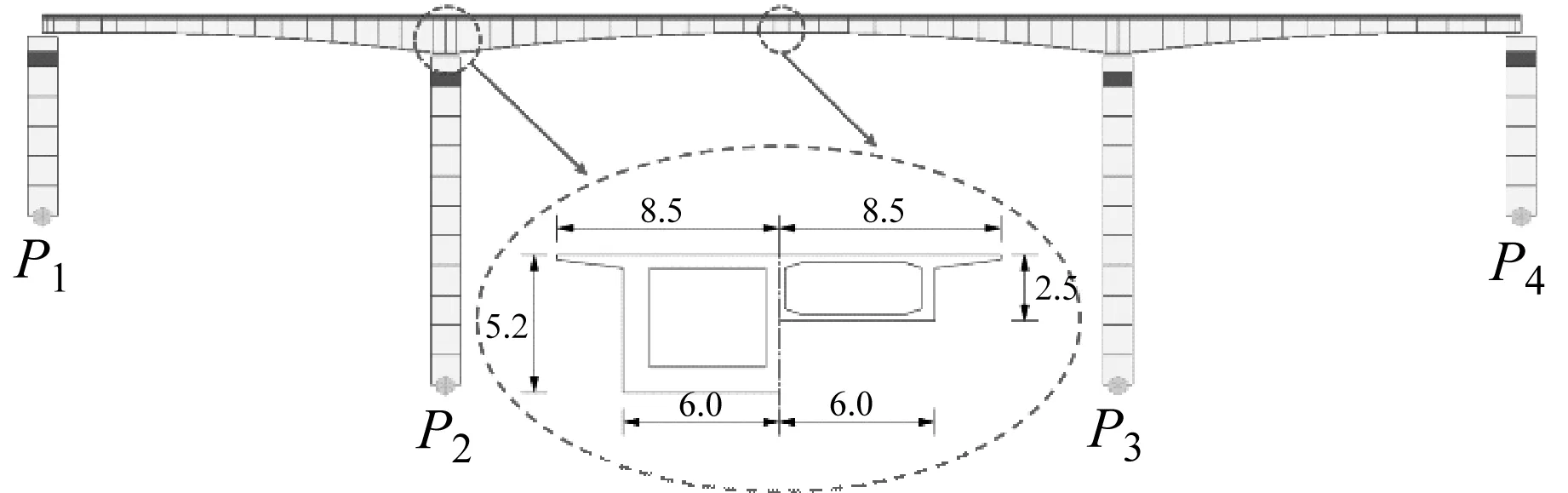
图4 三维有限元模型(m)
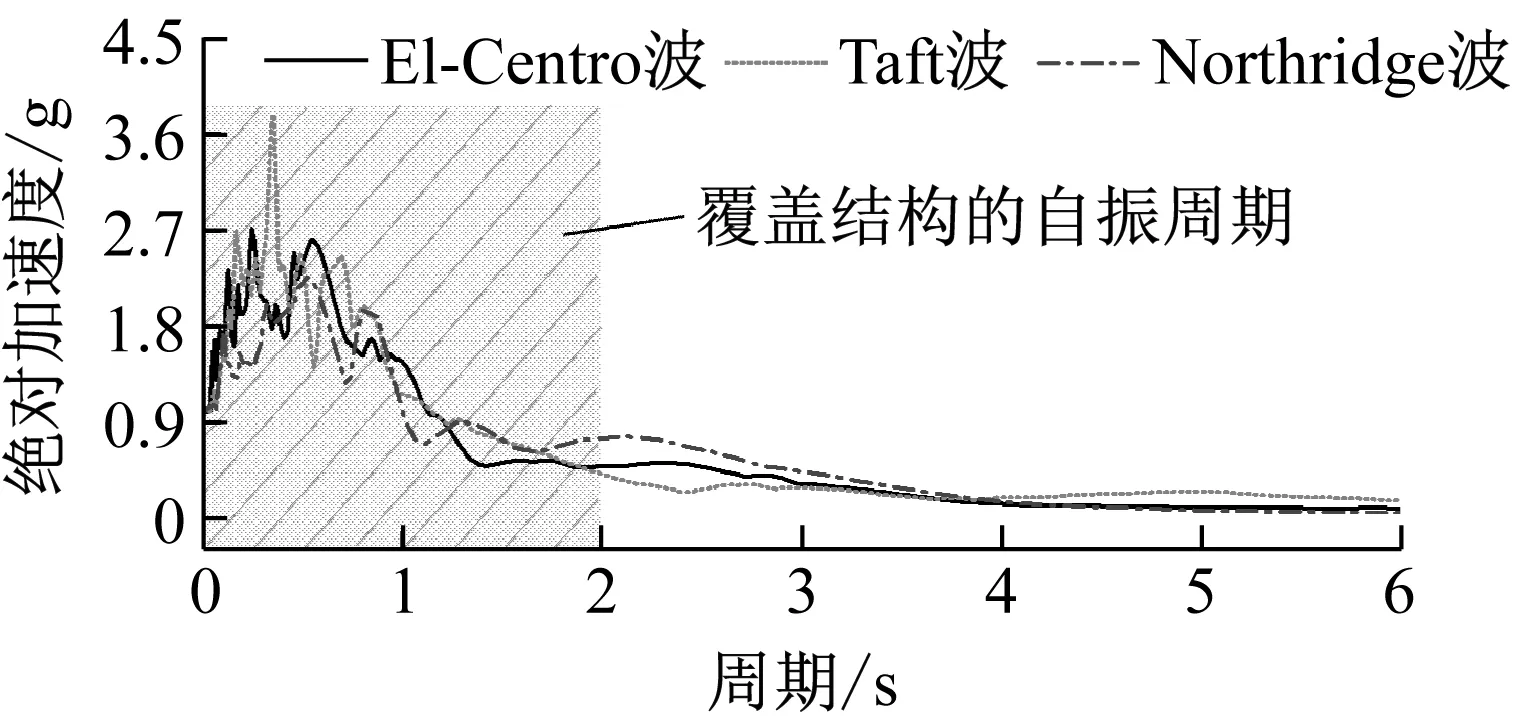
图5 加速度反应谱
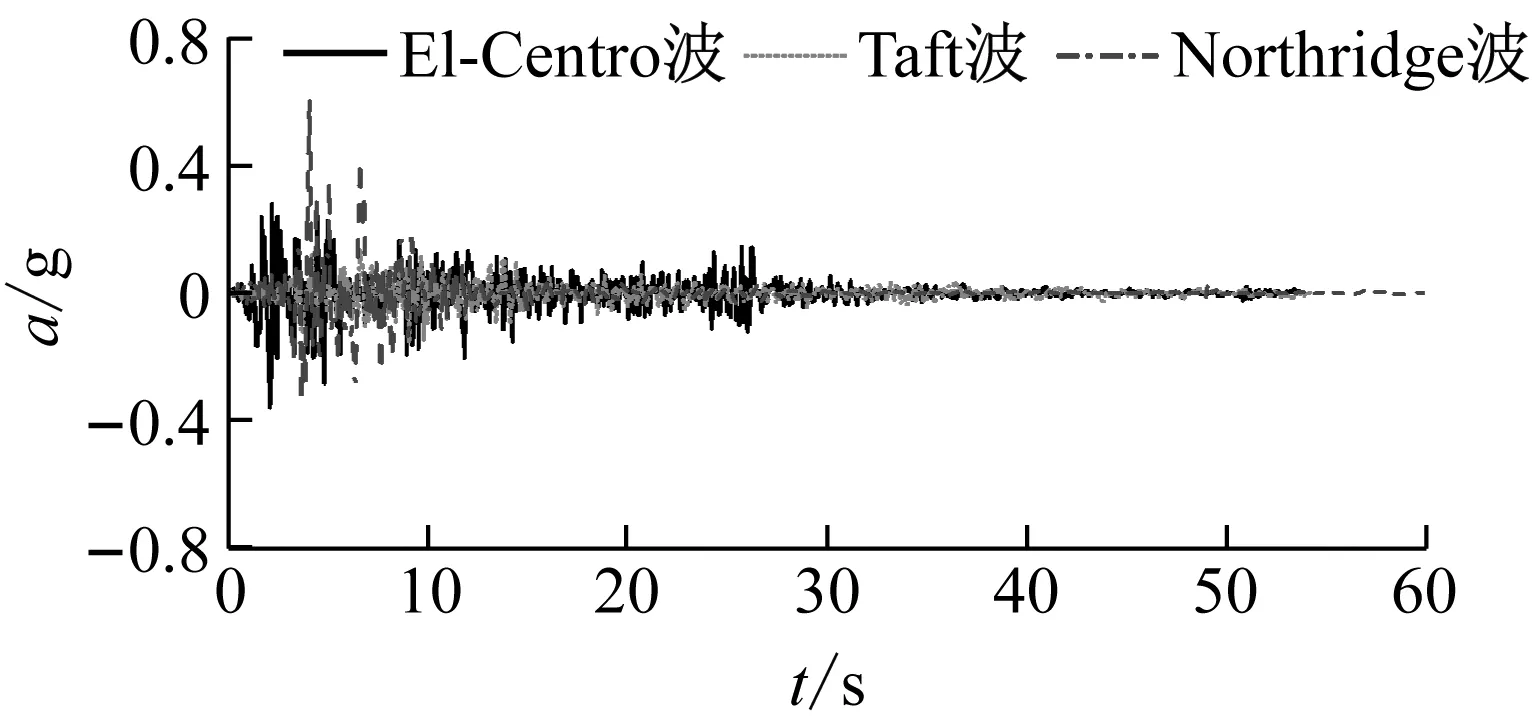
图6 地震动时程图
对于大跨连续梁桥,常用的隔震装置有铅芯橡胶支座和摩擦摆支座。为减小梁端位移,还可采用隔震和减震装置组合的方式,如铅芯橡胶支座+黏滞阻尼器。此外,鉴于摩擦摆支座实际工作时发生单摆运动,与提供轴向拉压阻尼力的黏滞阻尼器不完全适配,本文提出了摩擦摆支座和撑架组合的减隔震体系。几种减隔震方案的要点如下:
抗震方案,P1,P2,P3和P4墩均设置普通支承。
减隔震方案1,P1,P2,P3和P4墩均设置铅芯橡胶支座。
减隔震方案2,P1,P2,P3和P4墩均设置摩擦摆支座。
减隔震方案3,在减隔震方案1的基础上,在梁底和P1,P4之间增设纵向黏滞阻尼器。黏滞阻尼器的阻尼系数为3 000 kN·s/m,阻尼指数为0.2。
减隔震方案4,在减隔震方案2的基础上,在梁底和P2,P3墩两侧设置撑架。以撑架等效阻尼比9%为目标值,撑架长度为6 m,等效截面面积为1 100 mm2,采用Q160LY软钢,弹性模量为2.06×105MPa,屈服强度为(160±20)MPa。
其他参数如表1、表2所示。

表1 铅芯橡胶支座相关参数

表2 摩擦摆支座相关参数
3 动力响应及静力行为比较
3.1 动力响应对比
本文主要研究的是高墩大跨连续梁的内力位移双控体系,评价指标为墩底弯矩、墩底剪力和梁端位移。考虑到隔震装置和减震装置的非线性特征对结构地震响应的影响,采用非线性时程分析方法进行分析。假定该桥按地震基本烈度为Ⅷ度进行设防,分别沿纵桥向和横桥向输入地震动,地震动峰值加速度均调整为0.3g,得到抗震方案、减隔震方案1、减隔震方案2、减隔震方案3和减隔震方案4各桥墩关键截面动力响应,结构地震响应幅值取3条地震动的最大值,如表3所示。
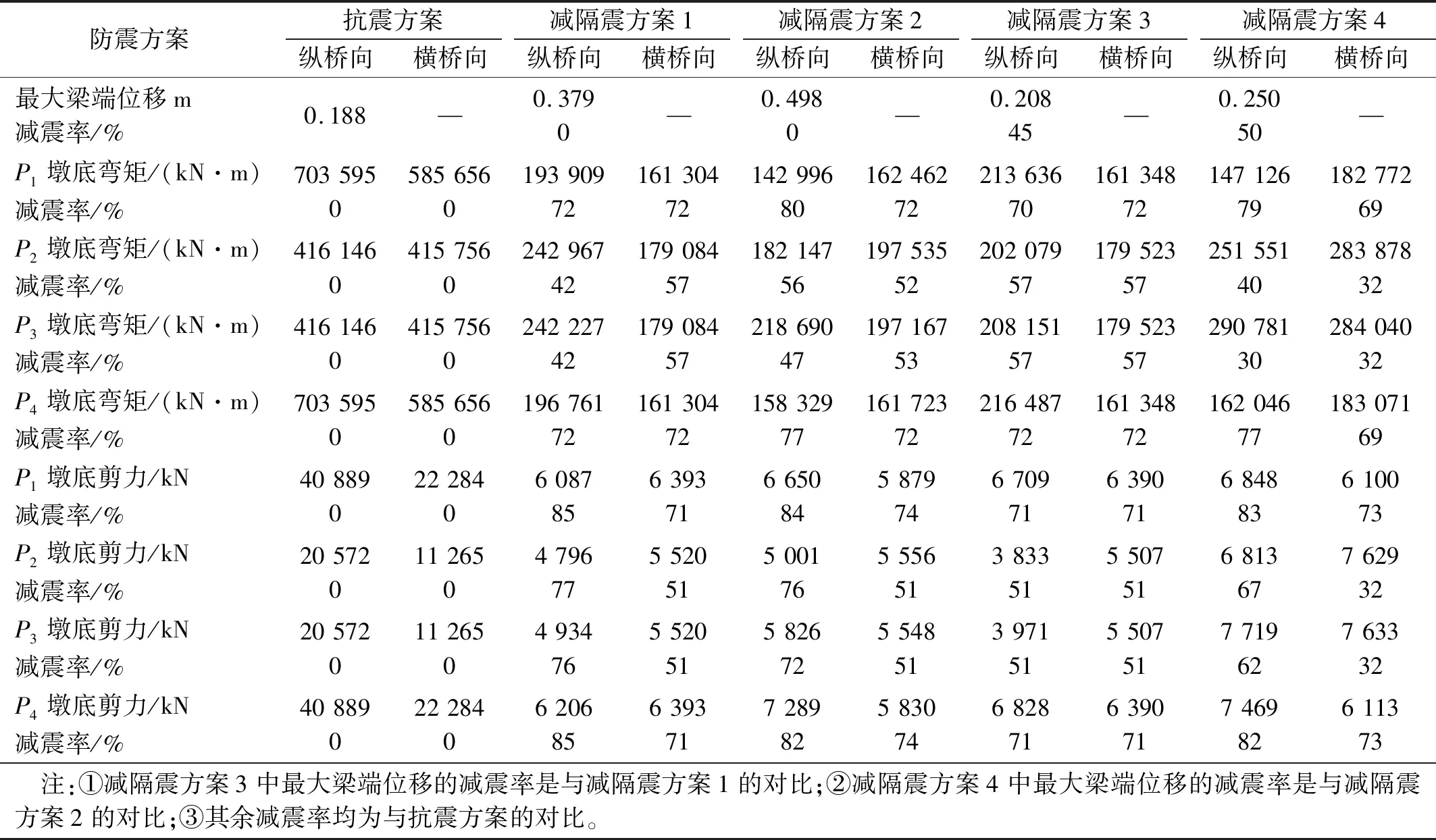
表3 各方案地震响应结果
3.1.1 墩底弯矩
相较于抗震方案,减隔震方案1和减隔震方案2均能显著减小各桥墩墩底弯矩,减震率分别为42%~72%和47%~80%,说明两种支座选型合适。在减隔震方案3中,相较于抗震设计,组合使用铅芯橡胶支座和黏滞阻尼器的桥墩墩底弯矩的减震率保持在50%~70%。减隔震方案3在减隔震方案1的基础上增设了黏滞阻尼器,阻尼器的阻尼作用使地震力在全桥进行了重新分配,P1和P4纵桥向墩底弯矩相对于减隔震方案1增大了10%,P2和P3弯矩则减小了17%,各墩横桥向墩底弯矩则无明显变化。这是因为本文在选用黏滞阻尼器时,主要考虑控制梁端位移,仅在纵桥向单排布置,阻尼力增大了由上部结构传递给桥墩的惯性力,导致P1和P4墩墩底弯矩有所增大、P2和P3墩底弯矩有所降低。
在减隔震方案4中,可以看到设置撑架后,与抗震方案相比,减震率在30%~79%。与减隔震方案2相比,各墩墩底弯矩均有所增加,增加率为13%~38%,增幅不大。其中中墩P2和P3的弯矩较边墩P1和P4的大,说明撑架在提供附加阻尼时还提供了一定附加刚度,提高了P2和P3墩的抗推能力,桥墩承受更大的内力,但P2和P3墩底弯矩与P1和P4墩底弯矩差距不超过19%。
3.1.2 墩底剪力
由表3可知,在抗震方案中,墩底最大剪力为40 889 kN,在减隔震方案1中,仅使用铅芯橡胶支座的最大剪力为6 206 kN,减震率为85%;在减隔震方案2中,仅使用摩擦摆支座的最大剪力为7 289 kN,减震率为82%。在减隔震方案3和减隔震方案4的双控体系中,桥墩墩底剪力峰值均有所增加,分别为6 828 kN和7 719 kN,仍远小于抗震方案的最大剪力。说明在高墩梁桥中,无论是采用黏滞阻尼器还是设置撑架进行减震,桥墩受到的剪力会有所增加,但这种增加在与隔震支座组合使用的减隔震方案3和方案4中相对较小,可以通过隔震支座进行控制。
3.1.3 梁端位移
表3显示了地震作用下,各方案在纵桥向的最大梁端位移,其中减隔震方案1和减隔震方案2的梁端位移均较大,分别达到了0.379 m和0.498 m,表明单纯的隔震设计会明显增加梁端位移,这是因为隔震设计使结构整体刚度变柔,通过释放梁体和桥墩之间的约束,将上部结构和桥墩隔离开来,使结构的变形集中到隔震装置处,从而减少墩底的内力。
在使用黏滞阻尼器后,减隔震方案3的最大梁端位移为0.208 m,相较于减隔震方案1减小了45%,但黏滞阻尼器的限位能力是以高的阻尼系数为代价的,阻尼系数太高会带来加工困难等问题。在设置撑架后,减隔震方案4的最大梁端位移降至0.250 m,相较于减隔震方案2减少了50%,可见撑架与摩擦摆支座组合使用可以有效限制梁端位移。
由以上对比分析可见:对于大跨高墩连续梁体系,减隔震方案3和方案4的减隔震效果明显优于减隔震方案1和方案2,铅芯橡胶支座与黏滞阻尼器组合而成的减隔震体系、摩擦摆支座和撑架组合而成的减隔震体系均具有较好的墩底内力与梁端位移的双控效果。但从震后复位能力来看,橡胶支座和黏滞阻尼器不具有复位能力,震后残余变形较大,而摩擦摆具有较好的限位复位能力,构造简单,性能可靠,且可以较方便地通过材料和几何参数来控制撑架所提供的附加阻尼和刚度,是一种适用于高墩大跨连续梁防震的双控体系。
3.2 撑架参数分析
撑架参数如截面积、长度等对减隔震体系的墩底内力、梁端位移双控影响较为明显,为此,选择不同撑架长度和等效截面面积两两组合分别建立有限元模型,以减隔震方案4纵桥向墩底最大弯矩和梁端最大位移为控制目标进行参数分析。
由图7可知:在相同的等效截面面积下,随着撑架长度l从6 m增加到10 m,墩底的最大弯矩逐渐减小,减小率分别为14%,15%和16%;在相同撑架长度下,随着等效截面面积A从1 000 mm2增加到1 600 mm2,墩底的最大弯矩则缓慢增加。其原因在于,对于设置撑架的桥墩,桥墩所分配到的地震力会增大,且附加刚度随等效长度的增加而减小,随等效截面面积的增加而增大。从图8中可以得到,随着等效截面面积和撑架长度增加,梁端位移均增大,限位效果变差。撑架的限位能力主要依赖软钢材料的屈服耗能,设计时主要根据梁端位移的设计需求,初步选择软钢材料,再通过撑架等效阻尼比公式选择合适的撑架长度和等效截面面积范围,在保证其限位能力的同时,避免各墩弯矩分布差异太大。
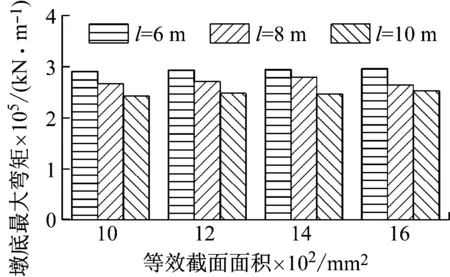
图7 不同撑架长度下墩底最大弯矩随等效截面面积的变化
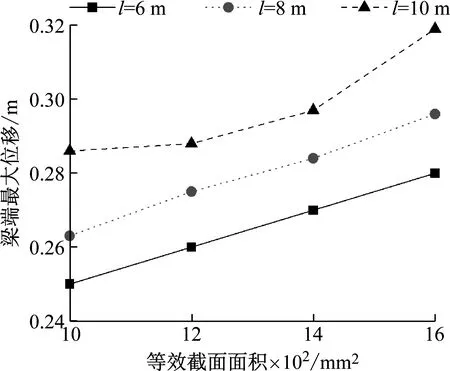
图8 不同撑架长度下梁端最大位移随等效截面面积的变化
3.3 静力性能分析
摩擦摆支座与撑架组合而成的减隔震体系,除了可以有效降低地震响应外,静力作用下梁体支点截面负弯矩峰值也可得到大幅度的削减,梁高和桥墩截面需求降低,动力响应还会进一步降低,起到良性循环作用。相较于减隔震方案2,减隔震方案4在P2,P3墩增设撑架后,在自质量和二期恒载作用下,支点截面负弯矩峰值从384 493 kN·m下降到280 681 kN·m,减小幅度高达27%(见图9),相应的,活载弯矩也会相应降低。初步估算,梁高可由原来的5.2 m降至4.6 m,由此也使桥墩尺寸相应减小,桥墩地震动力响应进一步降低。
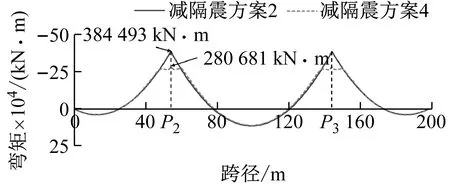
图9 恒载作用弯矩分布图
另一方面,从工程实施角度来看,铅芯橡胶支座与黏滞阻尼器组合减隔震体系中,铅芯橡胶支座尺寸较大,算例中铅芯橡胶支座直径为2 m,导致桥墩帽梁尺寸不得不随之增大,约为15 m×3 m,而对应的摩擦摆支座尺寸仅为1.07 m×1.07 m,帽梁尺寸为14.0 m×2.2 m,这一点随着墩高的增大,意义无疑是很大的。
4 结 论
本文提出了摩擦摆支座和撑架组合使用的减隔震体系,对于高墩大跨连续梁的墩底内力、梁端位移的双控具有突出的效果,在静力行为和施工方面也极具优势,初步研究的主要结论如下:
(1) 推导了撑架结构等效阻尼比的简化计算公式,基于此公式对撑架进行了参数分析,通过对铅芯橡胶支座方案、摩擦摆支座方案、铅芯橡胶支座+黏滞阻尼器减隔震方案以及摩擦摆支座+撑架减隔震方案进行了方案对比,验证了该体系对高墩大跨连续梁桥内力位移双控的有效性。
(2) 撑架的充分利用,永临结合,减少施工工序,同时降低了静力作用下支点截面负弯矩,梁高和桥墩的尺寸需求也会随着静力需求的降低而降低,动力响应进一步降低,起到良性循环的作用。
需要指出的是,本文仅对该体系的有效性进行了初步研究,其他问题如撑架选型、地震响应系统分析将在下阶段工作中进行研究。

