膜式空气弹簧帘子线铺设角-承载力映射模型研究

陈俊杰,谭月玲,康 盛,邱光琦

(江西理工大学 机电工程学院(汽车工程学院),江西 赣州 341000)

膜式空气弹簧(rolling lobe air spring,RLAS)工作时橡胶气囊沿活塞轮廓上、下卷曲,通过改变橡胶气囊的伸缩状态及内部压强获得弹性变形,设计过程中通过改变RLAS活塞形状、尺寸及橡胶气囊设计参量(帘子线铺设角、帘子线直径与间距等)可获取理想的RLAS迟滞非线性力学特性[1-2]。因RLAS变刚度、低自振频率、高度可控及良好的高频振动吸收、隔振能力,成为中高端汽车悬架广泛采用的非线性弹性元件[3-4]。

空气弹簧有效面积是其静、动态特性分析中的关键参数,目前研究主要集中在对活塞形状进行分类并通过几何关系推导出空气弹簧有效半径与高度之间的函数关系。郭继斌[5]针对用于列车的RLAS有效面积和有效面积变化率进行了研究,得出其近似计算公式。董学锋[6]通过对圆台型活塞RLAS进行几何结构分析,推导了RLAS有效面积计算公式。

唐传茵等[7-9]在董学锋的基础上,对不同活塞形状的RLAS有效面积开展研究,揭示了有效面积变化率及活塞主要参数对RLAS动态特性的影响规律。赵亚敏等[10]建立了约束膜式空气弹簧的改进刚度模型,考虑了弹性膜弧长变化引起的有效面积变化,为大承载、低频/超低频约束膜式空气弹簧优化设计提供了理论依据。

橡胶气囊设计参量对RLAS承载特性也有较大影响。橡胶气囊由帘子线和橡胶硫化而成,帘子线为气囊的主要承力元件,帘子线层的材料、结构、铺设角大小对空气弹簧承载能力和疲劳耐久性起着决定性的作用[11-12]。试验表明,帘子线铺设角将影响RLAS工作时橡胶气囊的膨胀外径,进而影响RLAS有效面积与承载能力,故研究帘子线铺设角与有效面积、承载力之间的映射关系对RLAS的承载能力设计与橡胶气囊工艺优化具有较重要的理论指导意义与工程应用价值。

胡双卫等[13]基于一阶剪切变形理论推导任意直四边形复合材料层合板的控制方程和一般弹性边界方程,研究了纤维铺设方式对板的固有频率影响。尹航等[14]考虑了RLAS有效面积与内压的关系,结合复合材料力学与几何学特征,从应力应变角度提出了一种车用RLAS有效面积理论分析及预测方法。揭示了空气弹簧气囊内压强、空气弹簧高度等因素对有效面积的影响规律。然而,该预测模型中未考虑到实际工作过程中帘子线角度变化的影响。本课题组采用几何与力学分析方法分别建立了囊式、膜式空气弹簧有效面积计算模型[15-16],为计算空气弹簧力学特性奠定了一定基础。

综上所述,现有研究主要通过几何关系推导RLAS有效面积数学模型,缺少从微观力学角度对多层气囊结构进行有效面积分析。同时,橡胶气囊充气膨胀变形,引起帘子线角度沿其气囊经线方向上发生改变,最终将导致有效面积变化,目前鲜有计及帘子线铺设角对有效面积的影响,导致空气弹簧承载特性预测产生偏差。针对上述不足,文中基于复合材料力学层合板理论及微元受力分析建立了车用RLAS帘子线铺设角-承载力映射模型,为橡胶与帘子线多层复合薄壁回转结构力学分析提供理论指导。

1 基于层合板理论的RLAS承载力模型

因RLAS工作时气囊沿活塞轮廓滚动,气囊支撑力很小而忽略不计,则RLAS承载力的计算公式[17]为

F=PeAeff

(1)

式中：F为承载力;Pe为RLAS囊内相对气压;Aeff为RLAS有效面积。

RLAS橡胶气囊由内、外层橡胶与内、外层帘子线层硫化形成,几何尺寸对称,与中面相对的单层板材料主方向和坐标轴的夹角呈现正负交替且对应厚度相等。由橡胶气囊实际内部帘子线铺设原理可知,其结构符合复合材料结构中的反对称角铺设层合板,故RLAS结构性质可由反对称层合板理论描述[18]。

图1为RLAS橡胶气囊膨胀后微元受力分析图,建立如图1坐标系,坐标原点为O,位于RLAS端盖中心。其中：t为气囊厚度;P为橡胶气囊内部绝对压强;R为气囊最大膨胀外径(即气囊最大纬线半径);dθ为微元纬线圆弧的长度dx所对应的圆心角,圆心为O1;dz为橡胶气囊经线方向所取微元高度,经向圆弧对应圆心为O2。dF1,dF2为横截面上微元长度经向/纬向上的内力。

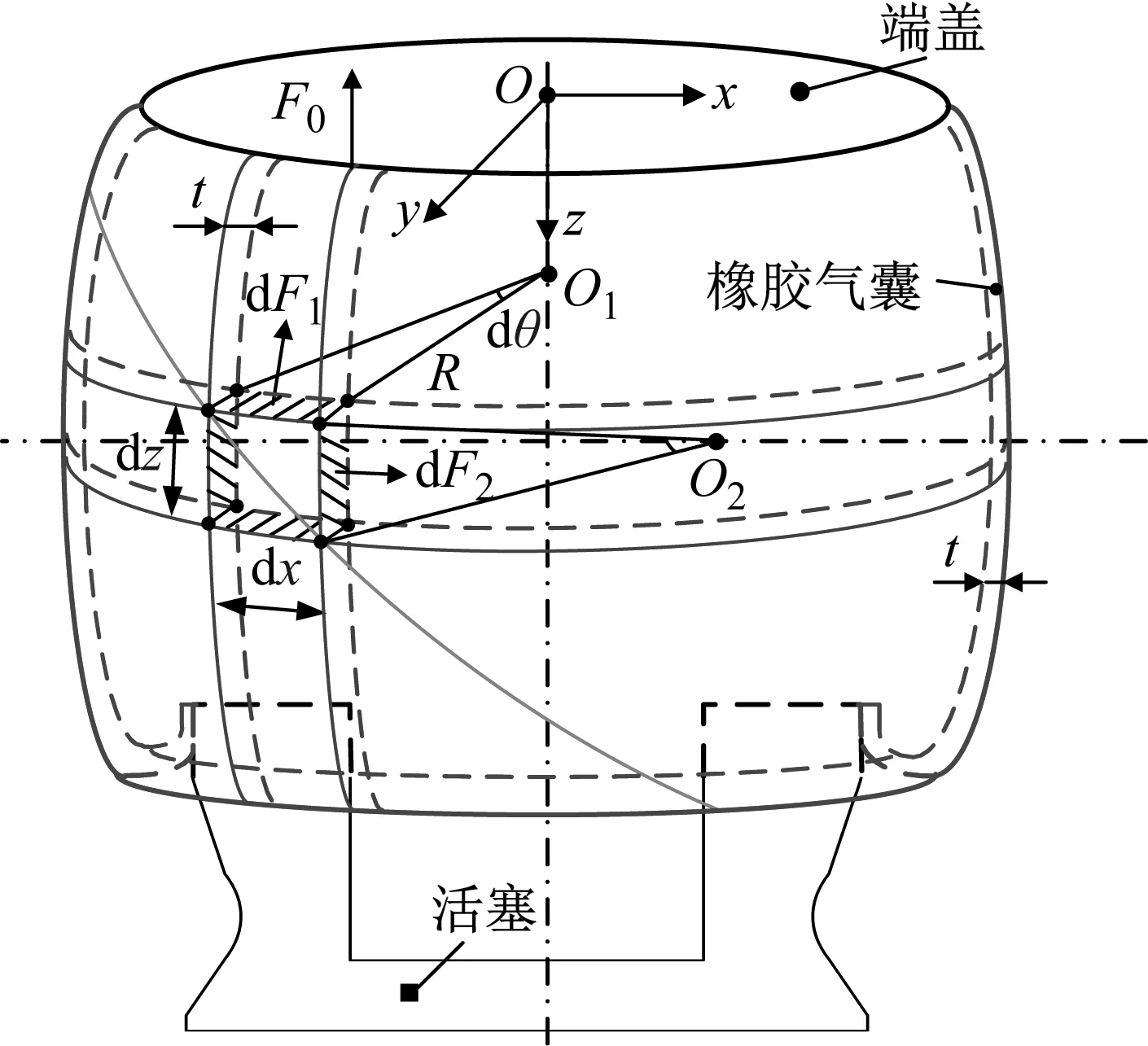
图1 RLAS橡胶气囊微元受力分析

在RLAS橡胶气囊高度方向选取高度为dz的微元,如图2所示。图3为所取气囊经线方向微元受力示意图。

图2 RLAS橡胶气囊横截面受力分析

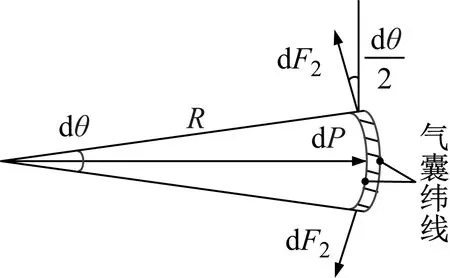
图3 微元横截面受力分析

由气囊受力平衡可得

(2)

式中：dP为气囊微元所受内压作用力;dθ为微元纬线圆弧的长度所对应的圆心角。

气囊在垂向上受到的与有效面积相关的拉力F0可表示为

(3)

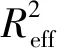
气囊微元在经向、纬向方向受到的力dF1,dF2可表示为

(4)

dF2=PRdz

(5)

令F1,F2为横截面上单位长度经向、纬向上的内力,有

(6)

F2=PR

(7)

图4为橡胶气囊内部帘子线铺设示意图,以内层橡胶帘子线层为例,方向1表示帘子线铺设方向,方向2为与方向1垂直的方向,方向3为气囊层板厚度方向,垂直于气囊平面。帘子线铺设角α为方向1与x轴夹角。

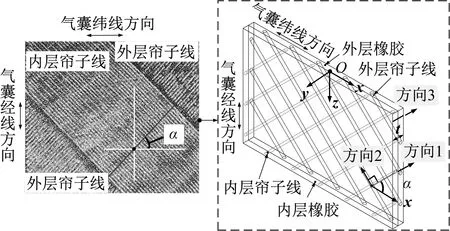
图4 橡胶气囊内部帘子线铺设示意图

根据橡胶气囊内部帘子线铺设示意图,定义：σi,εi分别为i方向的应力与应变,i,j=1,2,3;γmn,τmn分别为面i-j切向的应力与应变。mn=12,23,31。方向3(层板厚度t方向)厚度和其余平面内方向(1,2方向)尺寸相比很小,可近似为零,因此σ3=0,τ23=τ31=0,得到本构方程[18]为

(8)

根据材料力学二向应力状态分析,可用方向1-2坐标中应力分量表示x-z坐标中应力分量的转换。令图4中从x轴转向方向1为正,由受力平衡有

(9)

联立式(8)、式(9)可得本构方程

(10)

结合应力转轴公式可得与材料主方向成任意角度的x-z坐标系中的应力-应变关系如下

(11)

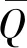
(12)

考虑到主要关注气囊x,z方向的宏观作用力产生的应变,忽略层合板扭曲率,x-z切向的应力应变τxz为零。空气弹簧橡胶气囊视为层合板结构满足材料力学中薄板定义[19],图5为层合板变形前后β角度变化情况,其中u0为C点变形后在x方向的位移。

(a)

气囊微元与应变关系满足小变形假设,则

(13)

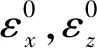
结合式(11),可得层合板中第k层的应力应变关系式

(14)

对层合板进行应力分析,假设Nx,Nz和Nxz为层合板横截面上单位宽度(或长度)上的内力(拉、压力或剪切力),应力方向如图6所示。文中主要分析橡胶气囊x,z方向产生的作用力Nx,Nz,忽略层合板扭曲率Nxz。

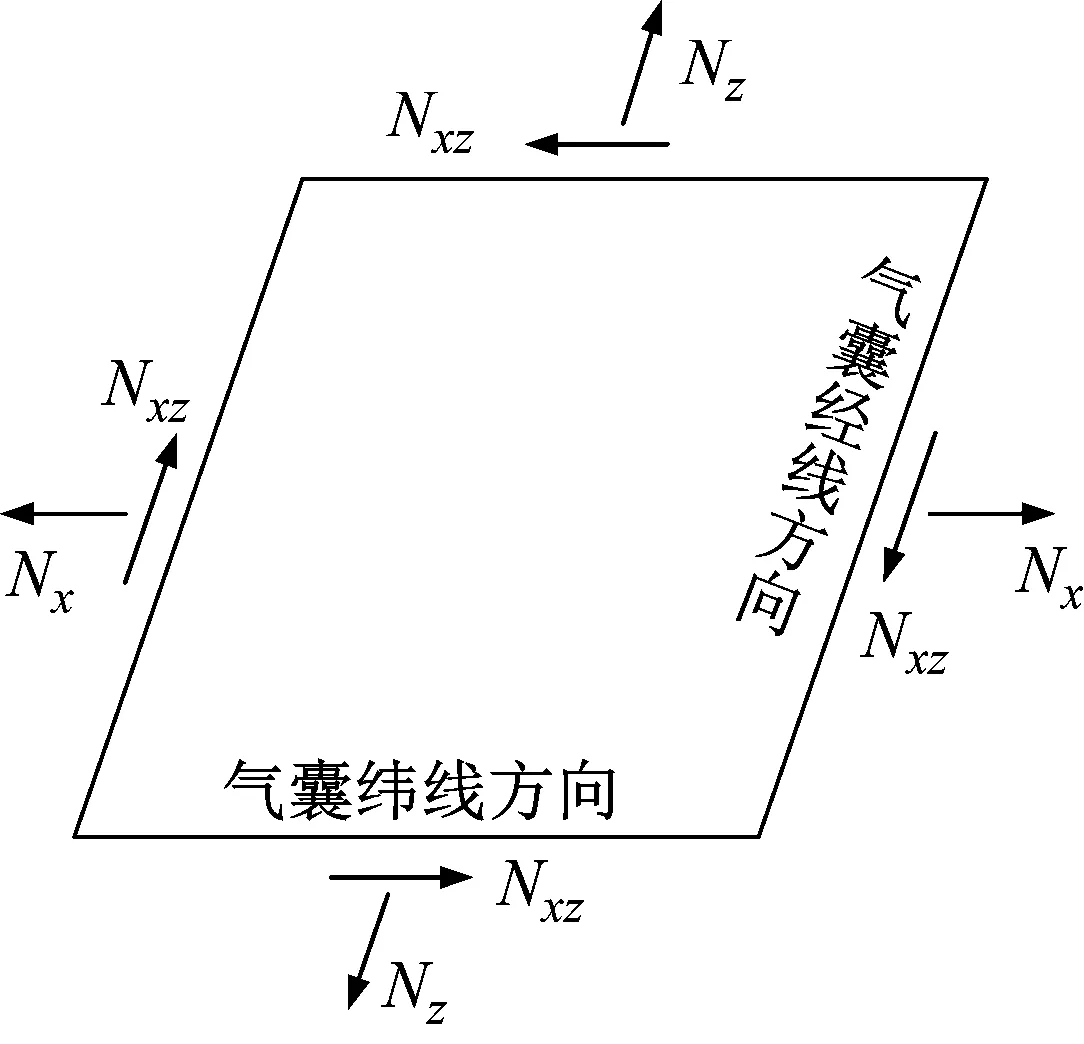
图6 橡胶气囊层内力示意图

内力Nx,Nz、内力矩Nxz与层合板应变之间的关系可表示为

(15)

其中

(16)

(17)

(18)

将式(18)简化得到橡胶气囊横截面上单位长度经向、纬向上的内力F1,F2与气囊应变关系式

(19)

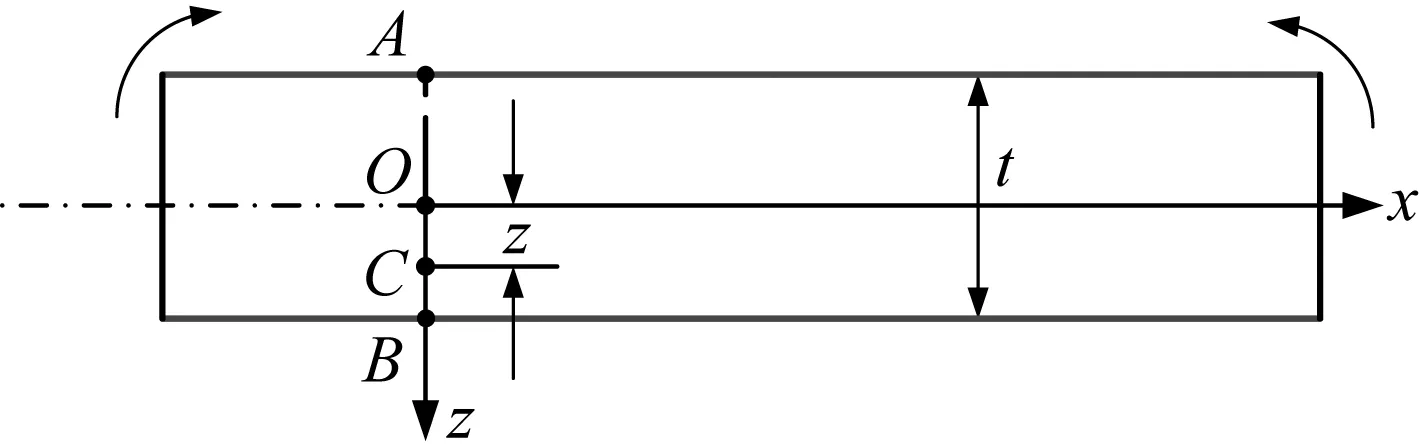
气囊x,z方向的应变

(20)

x方向为气囊纬线方向应变,是影响RLAS有效面积的主要应变方向,z方向是气囊沿活塞卷曲运动方向,与气囊最大膨胀外径尺寸无关,因此忽略z方向应变,仅考虑x方向应变,x方向应变可表示为

(21)

文中考虑到不同帘子线铺设角对气囊最大膨胀外径的影响,引入由帘子线铺设角影响的承载力系数M1(α),M2(α),计算公式如下

(22)

(23)

图7 橡胶气囊最大膨胀外径与应变关系图

R与R0气囊在x方向应变关系可表示为

(24)

结合式(21),得到RLAS帘子线铺设角-有效面积映射模型计算式为

(25)

同理,根据式(25)可得到RLAS帘子线铺设角-承载力映射模型表达式

(26)

式中：P为囊内绝对气压;Pa为标准大气压强,取值为1×105Pa。

2 模型验证与分析

2.1 试验装置及试验方法

为验证RLAS承载力计算模型的有效性,通过改变橡胶气囊工艺,选取帘子线铺设角分别为46°,51°和56°时样件A、样件B、样件C进行模型验证。运用MTS852.05弹性体测试台搭建了RLAS膨胀外径、承载力测试装置,试验仪器主要包括调压表、压强传感器、力传感器、位移传感器、开关阀及气源等,试验装置如图8所示。

图8 橡胶气囊膨胀外径、承载力试验装置

试验方法如下：试验时,在样件静平衡位置向RLAS内部充入绝对气压分别为4×105Pa,5×105Pa,6×105Pa,7×105Pa的压缩空气后关闭开关阀。不同气压下,样件A、样件B、样件C测试高度均为75～120 mm,试验速度为10 mm/min。由MTS数据采集软件可获取RLAS总成高度-承载力特性曲线与总成高度-气囊气压特性曲线。RLAS有效面积测试值由承载力特性曲线与气囊气压曲线相除可得。样件A相关设计参量如表1所示。

表1 样件A,B,C设计参量

根据式(13)、式(22)和式(23)计算得不同帘子线铺设角对应的承载力系数M1(α),M2(α)如表2所示。

表2 不同帘子线铺设角下承载力系数M1(α),M2(α)值

2.2 试验验证

图9给出了样件A在初始气压为4×105～7×105Pa的总成高度-气囊气压特性曲线。

图9 样件A在不同高度下气囊气压曲线

RLAS工作时高度发生变化,内部气压随之变化,进一步使橡胶气囊最大膨胀外径变化,由理论公式式(25)可知橡胶气囊最大膨胀外径R的变化会导致RLAS有效面积变化,进一步影响其承载力变化,因此在求解有效面积时需采用变化的外径进行计算。文中外径R由有限元方法计算获取[20-21],采用ABAQUS软件建立RLAS有限元模型,并运用Rebar单元模拟不同帘子线铺设角的橡胶气囊,可得不同初始内压和高度情况下的气囊外径值。

文中选取了样件A在任意两个气压下的试验与计算有效面积结果对比,如图10所示,两者最大相对误差为4.43%,吻合度较好,证明了本文推导的RLAS有效面积计算模型的正确性和有效性。

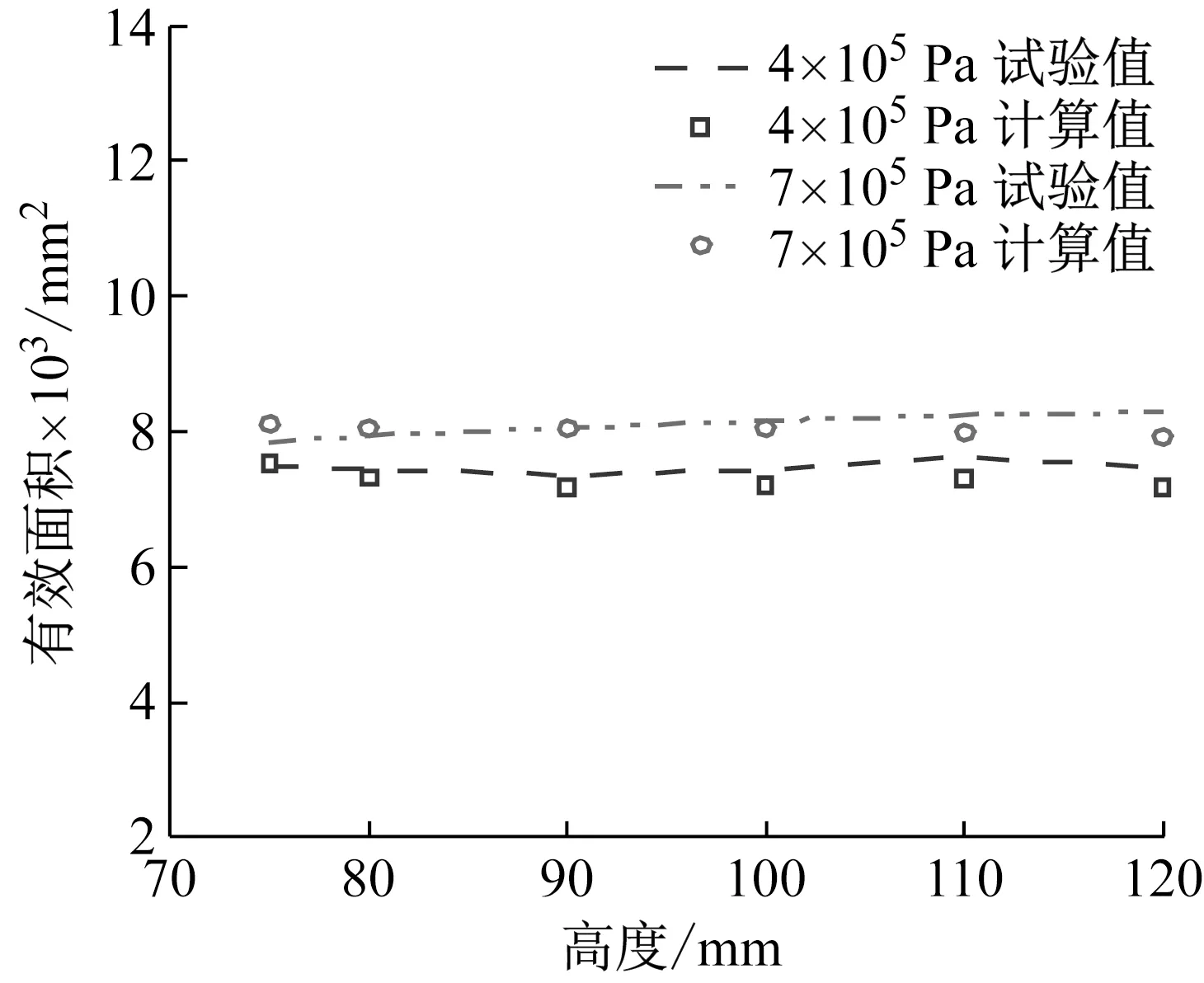
图10 样件A在不同压强下有效面积值

由图11可知,采用文中提出的帘子线铺设角-有效面积映射模型辨识得到的有效面积计算不同压强下RLAS承载力曲线与试验曲线对比可知,不同压强下的两种曲线簇基本吻合,不同压强下均一致呈现出承载力随RLAS总成高度下降而增加的趋势,有效表征了RLAS理想的力学特性,承载力最大相对误差为8.99%,验证了RLAS承载力映射模型的准确性。

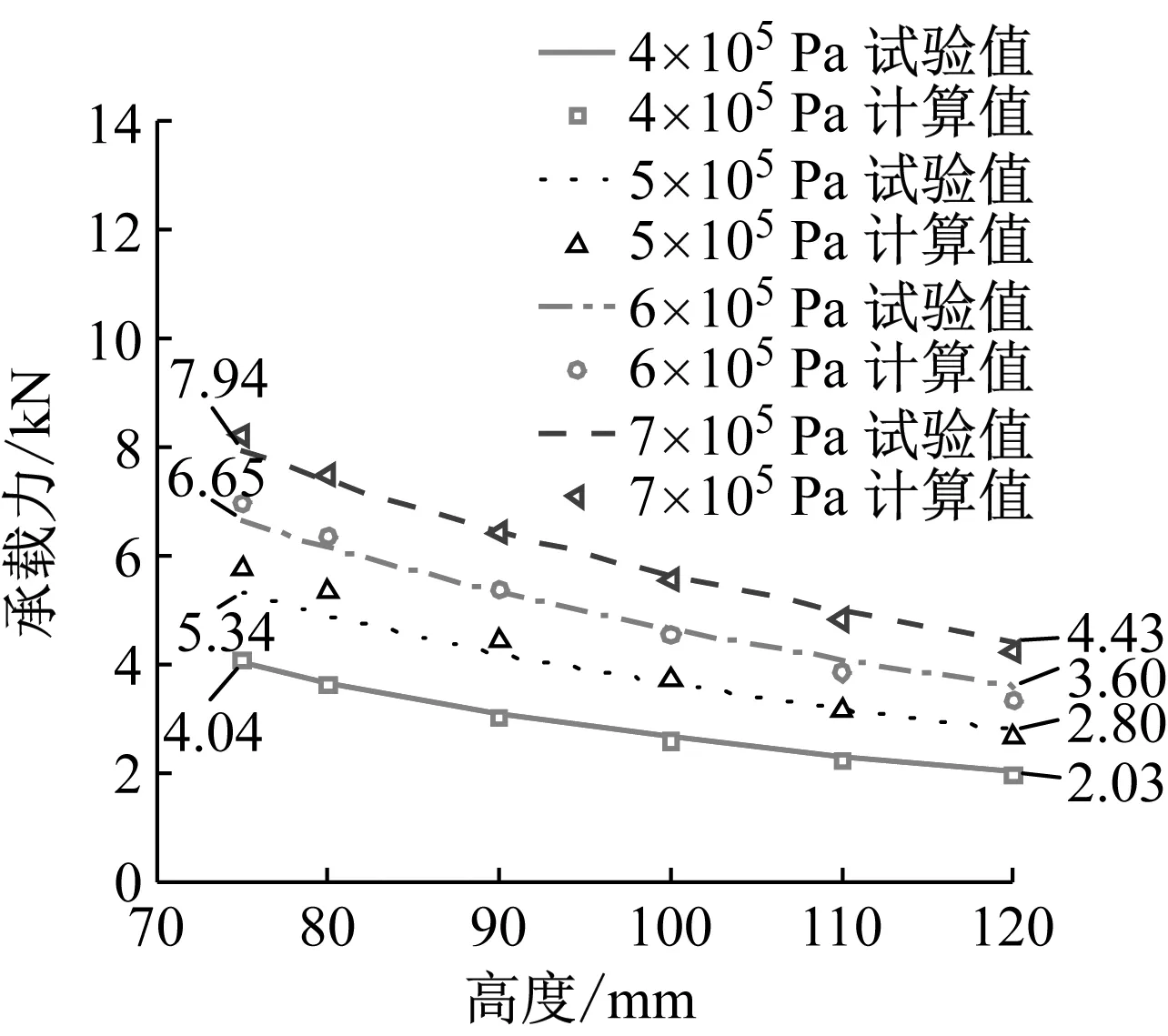
图11 样件A在不同压强下承载力对比曲线

根据式(26)计算可得橡胶气囊帘子线铺设角分别为51°,56°时RLAS承载力的计算值,计算值与试验值对比如图11、图12所示。当气囊内初始绝对气压为4×105～7×105Pa时,承载力试验值与计算值的最大误差分别为8.70%,9.18%,进一步验证了RLAS帘子线铺设角-承载力映射模型的准确性。

图12 样件B在不同压强下承载力对比曲线

图11～图13中标注了样件A、样件B和样件C在不同气压下承载力试验结果两端极值。对比图11～图13承载力结果及表3中承载力极差计算结果可知,在相同试验条件下承载力大小顺序依次为样件C、样件B、样件A,即当帘子线铺设角越大,RLAS承载力越大。同时,RLAS承载力极差,在相同试验条件下随着气囊帘子线铺设角增大而增大,即在帘子线铺设角设计合理范围内,帘子线铺设角度越大,RLAS承载力在某一工况下的变化范围越大。因此,橡胶气囊工艺制定过程中可通过改变帘子线铺设角-承载力映射模型中帘子线铺设角大小以获取所需的承载力范围,为合理设计帘子线铺设角及满足承载力设计需要提供科学指导。

表3 样件A,B,C在不同气压下的承载力极差

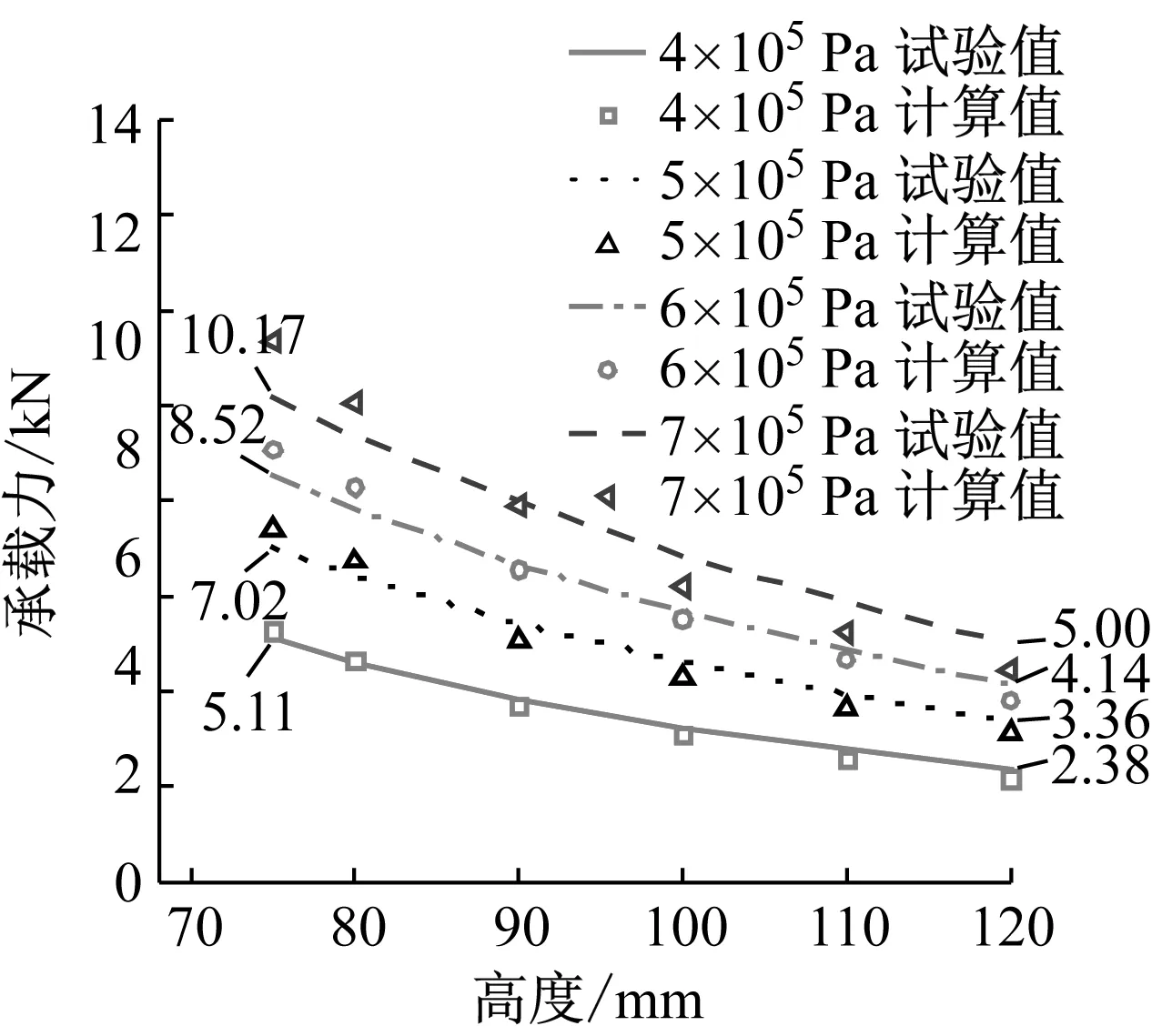
图13 样件C在不同压强下承载力对比曲线

3 结 论

本文基于复合材料力学层合板理论和微元受力分析,引入橡胶气囊帘子线铺设角,构建了RLAS帘子线铺设角-承载力映射模型。考虑了RLAS橡胶气囊工作过程中膨胀外径的动态变化,计算得到气压为4×105～7×105Pa时不同帘子线铺设角下的RLAS承载力最大相对误差仅为9.18%,不同压强下承载力曲线簇计算值与试验值一致性很好,精准预测了RLAS理想的非线性力学特性,验证了文中所提出承载力映射模型的正确性。最后,进一步分析了帘子线铺设角对承载力的影响规律,即在帘子线铺设角设计合理范围内,帘子线铺设角越大,RLAS承载力越大;其承载力极差亦随着气囊帘子线铺设角增大而增大,帘子线铺设角度越大,RLAS承载力在某一工况下的变化范围也越大。

研究结果为揭示膜式空气弹簧关键工艺参数-力学特性之间的映射机制奠定了理论基础,为优化膜式空气弹簧的成型工艺和承载特性提供科学指导。