图说数学跨学科教学

【摘 要】 跨学科教学是《义务教育数学课程标准（2022年版）》重点提倡的教学方式之一.借助图形讲解数学跨学科教学的几个基本问题：跨学科教学的地位价值、发展脉络、概念辨析、实施方法、评价方案等，并给出案例及剖析，帮助读者直观理解数学跨学科教学的研究成果，有效开展数学教学实践，稳步推进数学课程改革.

【关键词】 课程标准；跨学科教学；图说；理论；实践；辩证分析

细心的读者不难发现，“跨学科教学”是《义务教育数学课程标准（2022年版）》（以下简称《课标（2022年版）》）重点提倡的两种教学方式之一（另一种是“大单元教学”）^[1]86.为什么要提倡跨学科教学？跨学科教学的发展脉络是怎样的？跨学科教学的相关概念如何辨析？如何实施和评价数学跨学科教学？本文借助图形直观地回答上述问题，帮助读者理解新课标及其带来的教学方式变革.

1 跨学科教学的地位价值

要回答《课标（2022年版）》重点提倡“跨学科教学”与“大单元教學”^[2]两种教学方式的缘由，需分析它们的地位价值，这从《课标（2022年版）》的修订思路（如图1）中即可看出.

具体来说，就是《课标（2022年版）》以立德树人、核心素养为统领——育人为本、素养为魂^[3]，将数学素养与综合素养并重.其中，数学素养培育的载体是结构化的数学课程内容（具体包括“数与代数”“图形与几何”“统计与概率”3个学习领域），综合素养培育的载体是“综合与实践”（即第4个学习领域）.实际教学中，需要通过大单元教学落实数学课程内容的结构化，需要通过跨学科教学落实综合与实践活动.当然，大单元教学最终需要分解为课时教学才能进入课堂，跨学科教学最终需要主题活动（小学阶段）或项目式学习（初中阶段）来完成.最后，教师的教学、学生的学习均需依靠学业质量评价来检验、反馈、改善.

理解了《课标（2022年版）》的上述修订思路，我们就能明晰数学跨学科教学的地位价值，它承载着学生综合素养和实践能力培育的重任，绝非可有可无，它与大单元教学犹如鸟之双翼、人之双足，共同促进学生核心素养的发展，以致2022年版课程方案明确提出了“各门课程用不少于10%的课时设计跨学科主题学习”的刚性要求^[4].

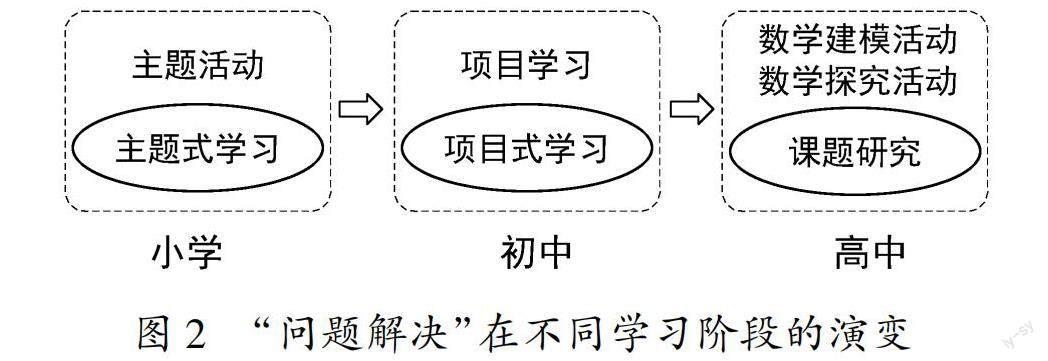
与数学跨学科教学的地位价值相关的一个问题是“综合与实践”在数学课程中的地位.比较2022年版义务教育数学课程标准与2017年版普通高中数学课程标准的课程内容结构^[5]，容易发现义务教育的4个“学习领域”与高中阶段的4条“学习主线”存在对应关系，体现了课程的发展与延续.其中，义务教育的“综合与实践”演变为高中阶段的“数学建模活动与数学探究活动”，它们是“问题解决”（Problem Solving）在不同学习阶段的表现形式（如图2）^[6]，也是课程综合性与实践性特征的集中展示.

《课标（2022年版）》指出，义务教育的“综合与实践”以“跨学科主题学习”为主，其中小学可采用“主题活动”和“项目学习”，初中可采用“项目学习”^[1]17.2017年版数学课标则指出，高中阶段的“数学建模活动与数学探究活动”包括“数学建模活动”和“数学探究活动”，两者都以“课题研究”的形式展开^[7]35.将这些名目繁多的学习方式统称为“项目/问题式学习”（Project-based Learning or Problem-based Learning，均简写为PBL），亦无不可，且与“问题解决”相呼应.

2 跨学科教学的发展脉络

跨学科教学的源头显然无从考证，但可以毫不夸张地说，自有分学科教学以来，就有跨学科教学，两者互为补充、相辅相成，正如实数轴上的有理数与无理数一样，它们相伴相生，共同构成完整的实数世界.

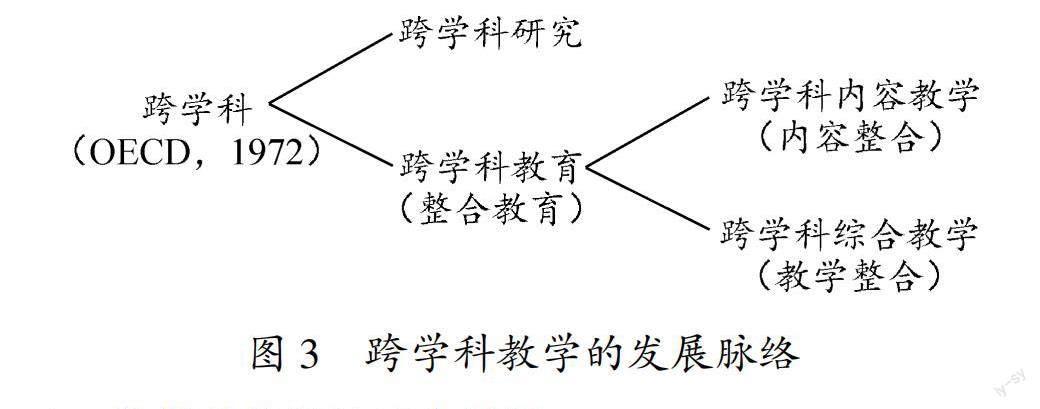
从有记录的文献来看，1972年的一次经合组织（OECD）会议明确将“跨学科”界定为描述两个或多个不同学科之间相互作用的形容词，这种相互作用的范围涵盖简单的思想交流到深度的结构整合^[8].后来“跨学科”继续分化为“跨学科研究”“跨学科教育”两个领域.其中，“跨学科教育”也称“整合教育”，它又分化为两个研究方向：一是将所有的科学学科视为一个整体，因为这些学科存在许多共同的概念结构和探究过程，且遵循普遍的规律；二是用综合方式教授不同的科学学科，便于实现一定的教学目的^[9].两个研究方向都注重整合，前者侧重内容结构的整合，后者侧重教学过程的整合^[10].两个研究方向都很重要，前者使得跨学科内容整合成为可能，后者使得跨学科教学成为现实.

这样我们就得到了如图3所示的一幅跨学科教学发展脉络.

3 跨学科教学的概念辨析

《课标（2022年版）》并没有给出“跨学科教学”这一概念的具体含义.仅从字面上看，至少需要厘清两个基本问题：跨什么？怎么跨？这需要我们结合多种研究文献和大量实践案例进行辨析.

关于“跨什么”，比较理性的认识应该是从数学学科“跨到”其他学科，并最终“跨回”数学学科.也就是说，问题可以来源于其他学科，但问题的解答根子还在数学学科.

根据《中华人民共和国学科分类与代码国家标准（GBT 13745-2009）》，可将数学跨学科教学问题的学科来源划分为自然科学、农业科学、医药科学、人文与社会科学、工程与技术科学等5类，具体如表1所示^[11].

因此，实施数学跨学科教学的一个基本前提是了解学科分类，以便选取相关的学科问题，设置相关的学科情境，运用相关的学科知识与方法解决问题.在实际教学过程中，我们无需纠结问题到底来源于哪个（哪些）学科，要重点关注问题能否实现数学化、能否获得数学的解答.

关于“怎么跨”，这需要将相关的四个概念（单一学科、多学科、跨学科、超学科）进行比较、辨析，如图4所示^[12].

其中，“单一学科”立即可以排除，它连基本前提“跨什么”都不满足.另外三个概念都满足“跨什么”，但在“怎么跨”方面表现出不同的整合程度.

“多学科”也应排除，不同学科围绕主题处于割裂状态，类似“水果拼盘”，学科之间没有发生相互作用更无整合.

“跨学科”的整合程度较好，学科之间相互作用、建立联系并产生新的理解，但探讨的问题往往局限在学科视野之中，较少讨论学科之间的交叉领域或关联部分.据此，有研究者认为“跨学科教学指的是让学生在对项目、主题、问题、任务等的实践探索中学习，将学科间的知识联系起来，作为一个整体进行学习的过程”^[13].这是目前较为普遍的一种认识.

“超学科”的整合程度最高，指向超越学科范畴的复杂问题解决，将学科间的关系置于一个完整的问题系统中进行认知，学科之间不仅实现了整合，还能产生新的解释性体系.这就是前面图3中侧重内容整合的“跨学科内容教学”，它与侧重教学过程整合的“跨学科综合教学”是两个不同的研究方向.

完成相关概念的辨析之后，我们在《课标（2022年版）》的背景下这样界定“数学跨学科教学”：它以数学学科为中心，通过问题或项目，将数学与其他学科的知识整合起来，侧重帮助学生深入学习数学的知识与技能、理解数学的思想与方法，并能创造性地解决应用性问题、综合与实践问题.数学跨学科教学的本质特征是促进学生思维（尤其是数学思维）的融会贯通^[14].数学跨学科教学，既可以发生在课内，也可以发生在课外；既可以用项目作载体，也可以用问题（包括例题、习题、考题等）为载体.

4 跨学科教学的实施方法

具体地，如何开展数学跨学科教学？我们分两种情况来讨论.

一是针对问题形式的数学跨学科教学.其实施的一般方法是：先从教材内容或考试素材当中选择数学跨学科教学的问题；充分挖掘该问题的数学教育价值；基于问题解决精心设计问题链；分阶段提前布置活动方案，学生自主学习、完成探索；引导学生使用规范的数学语言并辅以图文语言，进行学习成果的表达与交流^[15].

二是针对项目形式的数学跨学科教学.《课标（2022年版）》专门给出了3个初中案例（即课标附录1中的案例89，90，91），其中“体育运动与心率”这个案例很有代表性，贴近学生的生活实际，学生有兴趣、有能力去尝试、完成并获得一定的发展.该案例要求学生综合运用数学、体育、生物学等知识，研究体育运动与心率问题，可以作为初中数学“函数”主题中的跨学科项目学习.具体的问题交由学生自主提出，例如：在某种有氧或无氧运动中，运动类型、运动时间、运动员性别与心率的关系等.

该案例对跨学科项目学习的设计方案及实施流程都做了很好的示范，如图5所示^[1]171.对于其他相似跨学科项目学习案例，仅需替换图5中间方框的主题名称“体育运动与心率”以及虚线圆圈里的学科名称.

该案例以项目为载体，需要课内课外相结合，且具有开放性，没有“标准答案”.其中，课外主要完成问题的提出、方案的设计、数据的收集，课内主要完成数据的统计与分析，并综合运用函数、体育、生物学等知识分析数据之间的关系发现规律（数学模型）.该案例是以学生为主体、数学教师为主导完成的，应鼓励学生开展小组合作，必要时可邀请其他学科教师或班主任协同实施.

5 跨学科教学的评价方案

教学评价既是检验教学效果的方法，也是改进教学行为的手段.跨学科教学的评价方案应与跨学科教学的实施方案同步完成，确保“教—学—评”的一致性，以免最后流于形式.

有研究者综合理论认识和实践经验，给出了如图6所示的跨学科教学“三度”评价方案^[12].所谓“三度”包括指向学习内容的“学科整合程度”、指向学习过程的“学习投入程度”、指向学习结果的“问题解决程度”.该评价方案的一级指标之所以选定“三度”，理由是：“学科整合”是跨学科教学区别于其他教学方式的基本前提和特征；“学习投入”是跨学科教学有效开展的重要保障；“问题解决”是跨学科教学的直接结果.每个维度细分为若干二级指标，可以适当赋以分值或等第.跨学科教学完成之后，教师可采用文字语言或表格语言呈现每位学生或每个学生小组共同的表现性评价结果.

当然，跨学科教学评价方案的维度并不唯一，但都应立足跨学科教学（区别于其他学习方式）的基本特征，并与其教学目标保持一致.

6 跨学科教学的辩证分析

当前，随着《课标（2022年版）》的发布与实施，跨学科教学在数学教育领域如火如荼，但也出現了不少认识误区和操作盲点.实施数学跨学科教学需注意以下一些辨证关系.

（1）跨学科教学并非没有主学科，也不是多学科平均用力，数学跨学科教学要立足数学这个主学科，主要服务于数学学科的教学.

（2）数学跨学科教学不能以其他学科的知识应用、方法套用为主要目的.必要时，教师应引导学生深入所涉学科内部，了解该学科知识的来龙去脉，感悟该学科的思想方法.切忌生搬硬套、囫囵吞枣（貌似解决了一个个跨学科问题，但学生在跨学科的知识与思维方法上一无所获）.

（3）数学跨学科教学除了教学内容、教学形式的整合，更需要学生思维的整合.要避免跨学科教学流于形式，因为学生思维的综合化才是跨学科教学的精髓.还要避免跨学科教学内容或问题过于艰深、脱离学生实际.

（4）数学跨学科教学中要减少机械重复与无效的课外活动（如收集、统计价值不大的海量数据），减轻学生的学习负担，体现数学的学科价值与德育功能，正所谓“赢得了作业就赢得了学生”.

（5）由于数学跨学科教学本身的综合性以及实践操作层面的多样性，需要在实践过程中关注数学学科内容的落实、活动效率的保障以及评价指标的科学设计^[16].

本文通过“图说”数学跨学科教学，以期帮助读者直观理解其理论成果，有效开展教学实践，稳步推进课程改革.本文也是笔者“图说数学教育原理”文章系列^[2，5]的新成果.让我们共同努力，把数学教育理论变得更加直观形象，把数学教育研究变得更加平易近人.

参考文献

[1]中华人民共和国教育部.义务教育数学课程标准（2022年版）[M].北京：北京师范大学出版社，2022：86，16，171.

[2]刘祖希.图说数学单元教学[J].中学数学杂志，2022（07）：13-17.

[3]刘祖希.育人为本，素养为魂——《义务教育数学课程标准（2022年版）》之变化解读[J].数学通报，2023，62（01）：1-4.

[4]中华人民共和国教育部.义务教育课程方案（2022年版）[M].北京：北京师范大学出版社，2022：11.

[5]刘祖希.图说数学课程标准[J].中学数学杂志，2022（10）：1-5.

[6]郭衎，曹一鸣.综合与实践：从主题活动到项目学习[J].数学教育学报，2022，31（05）：9-13.

[7]中华人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2018：35.

[8]APOSTEL L.，BERGER G.，BRIGGS A.. Interdisciplinary： problems of teaching and research in universities [M].Paris：Organization for Economic Cooperation and Development，1972：25-26.

[9]刘仲林.交叉科学时代的交叉研究[J].科学学研究，1993，11（02）：9-16.

[10][美]冯·贝塔朗菲.一般系统论：基础、发展和应用[M].林康义，魏宏森，等译.北京：清华大学出版社，1987：75.

[11]宋燕伶，彭刚.北师大版高中数学教材跨学科内容研究[J].中学数学杂志，2022（01）：6-10.

[12]张玉华.跨学科主题学习的水平分析与深化策略[J].全球教育展望，2023（03）：48-61.

[13]王福瑞.跨学科主题学习的整合原则及路径分析[J].内蒙古师范大学学报（教育科学版），2023，36（01）：114-119.

[14]刘祖希.关于数学跨学科内容与教学的已有研究——兼及2022年全国高考数学试卷跨学科试题分析[J].教育研究与评论（中学教育教学），2022（12）：5-11.

[15]史嘉.综合与实践：以问题解决为导向的主题活动教学——以探究“纸折正五边形”为例[J].中小学课堂教学研究，2022（11）：64-67.

[16]孙虎，刘祖希.数学跨学科实践活动：“内涵”“价值”与“实施路径”[J].数学教育学报，2023，32（01）：19-24.[17]刘祖希.图说五种常用的数学教学法[J].中小学课堂教学研究，2020（5）：56-59.

[18]刘祖希.图说数学核心素养[J].中小学课堂教学研究，2020（10）：59-62.

[19]劉祖希.图说数学教育理论模型的建构[J].中小学课堂教学研究，2021（5）：60-64，67.

[20]刘祖希.图说数学教育研究方法[J].中小学课堂教学研究，2022（4）：65-68.

[21]刘祖希.图说数学教育理论的融通[J].中学数学杂志，2022（2）：6-10.

作者介绍 刘祖希（1980—），男，湖北仙桃人，华东师范大学出版社副编审，华东师范大学《数学教学》杂志编委，新青年数学教师工作室创始人，中国教育学会青少年创新思维教育分会常务理事，中国数学会数学教育分会中学工作组成员，倡导“让数学教育研究更加平易近人”;主编《当代中国数学教育名家访谈》等多部著作;在《中学数学杂志》等刊物发表文章100余篇.