动态几何环境中的证明与反驳
孙丹丹 栗小妮
【摘 要】 猜想、证明与反驳是数学发展过程中至关重要的数学活动,促进信息技术与数学课程的深度融合是2022年义务教育数学课程标准的基本课程理念之一.结合三个具体案例分析动态几何环境中的证明与反驳活动,阐述案例的背景、活动设计及价值,并一般性讨论了启发式反驳活动的教育功能.
【关键词】 信息技术;Geogebra;证明与反驳;反例
在数学发展过程中,新知识的形成往往要经过若干阶段,其中严密证明通常是最后一个阶段,在此之前,数学研究者首先需要识别和重组一些重要的事实成为有意义的模式,基于模式形成猜想,然后以新的事实或证据验证猜想,并可能需要修改猜想以回应反例,最后才解释及论证事物是否及为什么以某种特定方式运行[1].数学学习的过程应该反映数学创造的过程[2],然而,在中学数学中,证明经常以一种完成了的标准形式化的方式呈现,没有其他数学活动支撑,这导致即便是对一些数学表现很好的学生而言,数学证明也仅仅是技巧的组合,而非加深其数学理解的必要活动.如何设计包含猜想、证明与反驳的课堂任务以增进学生对数学证明活动本质的认识及逻辑推理素养的提升是本文的讨论主题.
动态几何环境是指可动态处理几何图形的信息技术环境,依赖于特定信息技术软件,如Geogebra、网络画板等.在动态几何环境中,学生很容易接触到各种各样的数学实例,这些实例很难在非信息环境或静态几何环境中构造[3],根据多样的实例,学生更可能做出数学猜想.此外,动态几何环境的另一优势是可通过拖动几何对象等操作实现对象的连续变化,相比一系列离散的实例,连续变化的实例更有利于支持学生洞察变化表象中的不变和突变属性.基于以上特性,动态几何环境可能会对学生数学证明过程提供有益支撑.本文尝试分析动态几何环境中包含猜想、证明与反驳的数学证明活动设计及这种活动设计的教育价值.
1 启发式反驳
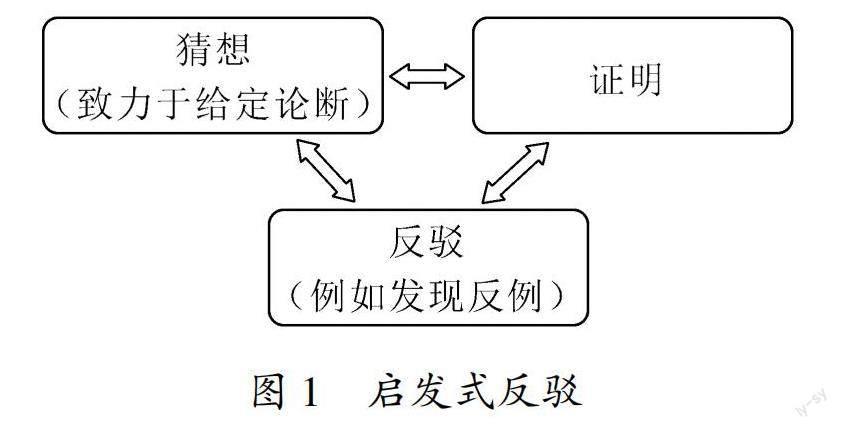
在《证明与反驳》一书中,拉卡托斯论述了非正式的、拟经验的数学不是通过一味增加确定无疑的定理而发展的,而是通过猜想和批判、证明和反驳而发展的[1]168.数学家做出猜想或致力于一个给定的论断,然后尝试证明,在此过程中,会面对猜想、论断以及证明的反驳,通过处理这些反驳来修正猜想、论断以及证明,如图1所示,启发式反驳强调了猜想、证明与反驳的交互,这在数学发展中起着至关重要的作用.
启发式反驳最初指基于反例修正猜想或论断,后来将证明过程也作为反驳对象包括在内,启发式反驳的定义拓展为发现猜想或证明的反例,并通过解决反例来修正猜想或证明[4].值得说明的是,这里证明的含义是广义的,包括非形式化的证明,也包括部分情况下猜想或论断的演绎证明.与此对应的,反驳是指对猜想的真实性或证明的有效性提出质疑,反驳的对象不仅仅是猜想,也包括证明.拉卡托斯强调了证明与反驳的密切关联,并将反驳证明中某步骤的例子及反驳猜想或论断的例子分别称为局部性反例及全局性反例[1]6.什么时候会出现反驳证明中某步骤的局部性反例呢?一个有待证明的数学命题通常借助一个给定的图形来描述,该图代表了某种一般的情况[5].然而,所画的图虽然是一般的,但仍然是单个、具体的,所以它虽然在某种程度上有普遍代表意義,但并不一定可以囊括命题描述的所有情况.这就造成证明过程可能隐含了某种假设,这种假设适用于该图形代表的情形但不适用于命题描述的所有情况,由该图形得到证明在其他某些特定情况下可能会失效.将给定的图形转化为满足命题前提的不同图形便可能生成证明的一个局部性反例,它可能反驳已有证明的某一步或某几步,促进证明的修正完善.
启发式反驳的意义不仅仅是反驳,因为它不仅包括发现反例以说明猜想或证明的错误,更重要地,它还包括通过反例对猜想和证明进行修正[4].启发式反驳中,学生存在的困难之一是发现猜想、陈述或证明的反例,因此,在启发式反驳相关任务设计中,给学生提供工具辅助学生创造及发现反例非常重要,动态几何环境蕴含这种潜能.在动态几何环境中,学生可以选择一个或多个对象,在屏幕上连续拖动它们改变图形,生成反例.
2 案例及分析
下面将通过三个案例来阐述动态几何环境支持下的证明与反驳活动,讨论活动实施的必要性及价值.
2.1 反驳证明过程活用旧知——圆周角定理
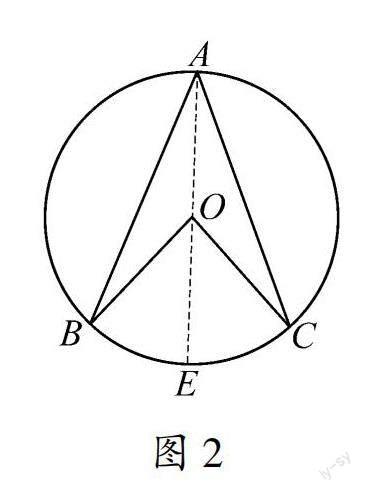
圆周角定理是有关圆的一条重要定理.教材在给出圆周角定义后,往往引导学生测量发现同一条弧所对的圆周角的度数等于它所对的圆心角的一半,然后尝试严格证明,检验猜想.实际教学中,在进行测量和得到猜想及证明之前,学生需要首先根据已知条件作图,画出一条弧所对的圆周角及圆心角,学生的一般作图及常见辅助线构造方法如图2所示.
证明如下:连接并延长AO,交圆于点E,因为AO=OB,所以∠BAO=∠ABO,同理,∠CAO=∠ACO. (1)
∠BOE=∠BAO+∠ABO=2∠BAO,同理,∠COE=2∠CAO. (2)
所以,∠BOC=∠BOE+∠COE=2∠BAO+2∠CAO=2(∠BAO+∠CAO)=2∠BAC. (3)
上述方法证明了同一条弧所对圆周角是圆心角的一半,但依赖于图2所示的圆周角与圆心角的位置关系.图2所示的同弧所对的圆周角和圆心角位置关系是否具有普遍性?是否还存在其他情形?其他情形下以上证明是否还成立,对应的,圆周角与圆心角关系猜想是否还成立呢?这些问题的回答均依赖于对证明的“反例”的探寻.教师虽然可以直接给出所有同弧所对的圆周角和圆心角的可能位置关系,但信息技术环境有利于提供学生自主发现这些不同可能的机会.
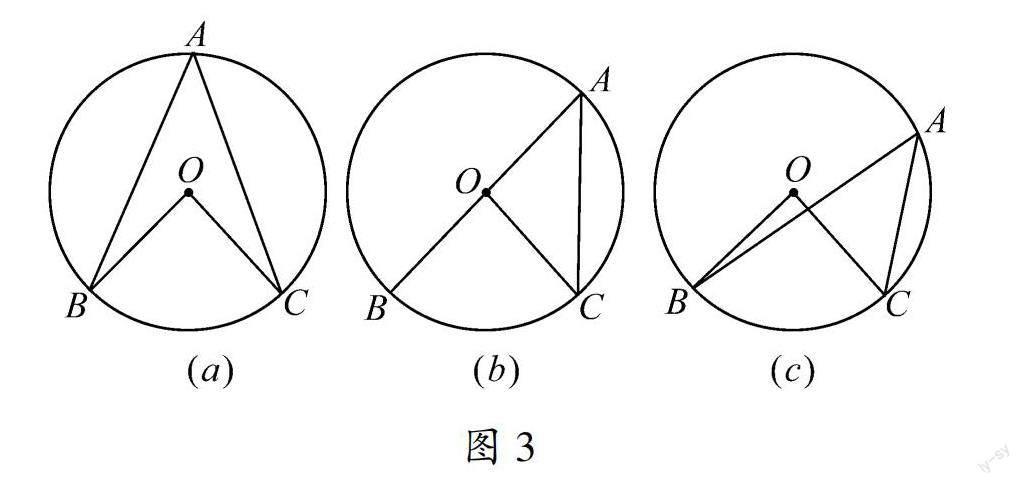
如图3(a)所示,在Geogebra软件中,作一圆O,作弧BC所对的圆心角BOC及圆周角BAC.点A可在圆O上被任意拖动改变位置,动态图见https://www.geogebra.org/m/ykcprgqj.教师可给出任务及问题:在圆O上移动点A,之前的证明过程是否一直成立?有关圆周角和圆心角关系的结论是否一直成立?为什么?在学生拖动点A的过程中,圆周角和圆心角的位置关系不断连续变化,可很多情况下上述证明仍然适用,直到学生将点A拖动到BO或CO的延长线上(如图3(b)所示),继续拖动点A,还有另外第二种新的位置关系出现(如图3(c)所示).在两种新的同弧所对圆周角和圆心角位置关系中,原有证明失效,局部性反例出现,学生必须尝试在这两种情境中调整或修改证明中的一步或若干步,来判断一般性猜想是否成立.
信息技术的价值在于提供了一个可以让学生自主发现“局部性反例”的环境,让学生体会到发现的乐趣,而不是被动接受,而且由于学生可连续拖动圆弧上的点A,学生也可以感受到除了图3所示的三种位置关系外,不存在其他证明的“局部性反例”.虽然图形的位置关系发生变化,导致原来的证明不再有效,但原图形中某些位置关系被保留了,所以原有的证明可以为新情形下圆周角与圆心角关系证明提供启示,学生需要思考原有证明哪些步骤仍然是成立的,哪些需要做调整.
以图3(c)所示圆周角与圆心角位置关系为例,仍然采用原有辅助线作法,如图4所示.原证明步骤(1)(2)中角的关系并未变化,关键变化在于∠BOC不再是∠COE与∠BOE的和,而是∠COE与∠BOE的差,∠BAC也不再是∠CAO与∠BAO的和,而是∠CAO与∠BAO的差,如此,较容易改变步骤(3),修改原有证明使其适用于新的情形.在这个过程中,学生首先在较为熟悉的问题情境中解决问题,然后在局部性反例的推动下,基于已有问题解决经验,灵活运用已有知识处理相对陌生情境中的问题.
2.2 反驳证明过程促生新知——圆内接四边形性质
北师大版初中数学教科书在九年级下册圆周角与圆心角的位置关系一节,首先给出了圆周角定理,随后引导学生探究圆内接四边形的对角的关系、圆内接四边形的任意一个外角及其内对角的关系.学生不难在教师的指引下一步步运用原有知识解决新问题,但可能会对新问题解决的动机不足.如下两问题有助于激发学生探索欲望,实现两部分内容的整合及过渡.
(1)如图5所示,圆O上有四点A,B,C,D,作直线AC和BD,交点为E,△AEB和△DEC是否相似?写出证明过程.
(2)在动态几何环境中作问题(1)所示图形,在圆O上移动点A,B,C,D,思考:问题(1)中的证明过程是否一直成立?问题(1)中两三角形关系的结论是否一直成立?
在图5所示情形中,问题(1)的证明需要用到圆周角定理,具体证明过程如下:
因为∠AEB=∠DEC(对顶角相等),∠BAE=∠CDE(圆周角定理),所以△AEB∽△DEC(两对应角相等,三角形相似).
问题(2)提示题目中A,B,C,D四点的位置关系并非只有图5所示情形,其他位置关系可能构成以上证明的局部性反例或以上命题的全局性反例.反例的寻找是难点,信息技术环境使这种系统的搜索成为可能,在动态数学软件Geogebra中,作圆O,在圆O上任取A,B,C,D点,四个点均可以在圆O上自由拖动,动态图见https://www.geogebra.org/m/nyevzyre.拖动点A,B,C,D,可以发现不同的位置关系,出现原证明的反例,课上重点讨论图6所示情形,其余情形较为简单,可留作课下自行讨论.
在图6所示情形中,∠AEB和∠DEC不再是对顶角而是同一个角,所以虽然与问题(1)的证明论据不同,但∠AEB=∠DEC仍然成立.∠BAE和也∠CDE不再是同弧所对的圆周角关系,而是圆内接四边形的一个外角及其内对角的关系,两者是否仍然相等不再显然,需要更多推理来证实或反驳.
通常教学在圆周角定理学习后直接引导学生分析圆内接四边形对角关系,然后分析圆内接四边形外角与内对角关系.每个问题要证明什么及用什么来证明都比较明确,问题难度小,可较快速得到结论.这里将两个问题,连同圆周角定理的应用,共同嵌入在一个启发式反驳活动过程中,由于圆内接四边形对角关系与内接四边形外角与内对角关系密切相关,后者是前者的显然推论,所以不将其拆解为两个任务,直接讨论圆内接四边形外角与内对角关系难度也不大,可以给学生多一點自主分析的空间.更重要地,在应用圆周角定理得到问题(1)的结论及证明后,由于问题条件具有不确定性,在动态信息技术支持下学生可变式出更多图形关系,出现局部性反例,推动启发式反驳,自然创造探究新问题的契机.在这样的活动中,局部性反例是学生自己在操作中发现的,新情境与原结论之间的冲突促使学生进一步分析问题,锁定问题关键——圆内接四边形对角是否互补,促使新知识的诞生.
2.3 反驳已有猜想完善新知——三角形全等判定
全等三角形是初中重要主题,是图形与几何领域培养学生逻辑推理能力的重要载体.三角形全等学习的难点之一是两边及其中一组等边的对角相等可否判定三角形全等.北师大版初中数学七年级下册引导学生作两条边长分别为2.5cm和3.5cm,且长度为2.5cm的边长所对角为40°的三角形,并给出图7所示两个三角形,接着给出结论:“两边分别相等且其中一组等边的对角相等的两个三角形不一定全等”.
仅根据图7,学生最可能得到的猜想是:两边及其中一组等边对角相等的三角形不全等.两边及其中一组等边的对角相等的两个三角形究竟是一定不全等还是不一定全等?如果不一定全等,何时会全等?教材给出的只是一个特殊的边角关系实例,学生需要更多实例检验或修正最初猜想,信息技术环境有利于学生自主生成这样的实例.
如图8(a)所示,拖动点D可改变圆的半径,动态图见https://www.geogebra.org/m/zj3xprm5.教师可给出任务及问题:为什么要以C为圆心作圆?改变圆的半径,圆与射线AB的交点个数有几种可能?这说明怎样的问题?
教材给出的三角形两边长及其中一组等边所对角度是一种特殊情况,在这种情况下,两边及其中一组等边所对角相等,三角形不全等,但拖动点D很容易生成反例,这种反例是拉卡托斯所说的全局性反例,即可以反驳原有猜想的反例.反例之一如图8(b)所示,随着圆的半径不断增大,当半径大于等于AC长度3.5cm时,圆与三角形一边所在射线AB只有一个交点,这说明满足这种条件时作不出两个不同形状的三角形,也即两条边长分别为3.6cm和3.5cm,且长度为3.6cm的边长所对角为40°的三角形必全等,反驳原有猜想“两边及其中一组等边对角相等的三角形不全等”,将新知修正完善为“两边及其中一组等边对角相等的三角形不一定全等”.除图8(b)所示情形,当圆与射线AB相切时,圆的半径为一特定值,此时圆与直线的交点也只有一个,满足特定条件的三角形也只有一个.
3 意义与价值
信息技术使图形变换轻而易举,图形变换易生成反例,而反例是开启反驳活动的钥匙.反例类似一种变式,促使学生处理更加复杂或陌生的情境,灵活运用旧知解决问题.当学生不能使用已有结论处理反例时就创造了新知学习的需求,在此过程中有可能解决新问题从而验证猜想,也可能反驳修正了原有猜想,完善新知识.
证明与反驳过程有利于激发学生内在探究动机.反例呈现的新情况与原有猜想及证明过程的对比促使学生产生认知冲突,这种冲突促使学生进一步探究问题解决方式.此外,反例的生成是反驳过程的必要前提,因为每种动态几何软件都有通过拖动点和线直接改变图形的功能,所以动态几何环境可助力学生创造各种图形,进而支持学生自主发现反例.如此,教师结合教学目标设计适当难度的任务和问题,学生可在动手操作与理性思考中自主推进整个探究过程.
证明与反驳过程有利于锻炼学生数学推理能力.已有研究指出学生对猜想所得结论进行反思和检验的能力不足,需要设计高层次的数学合情推理活动,让学生经历获得猜想、检验猜想、加强或推翻猜想,乃至证明猜想的全过程[6].本文案例是这方面的尝试,学生首先生成初步证明或猜想,然后在信息技术的支持下发现反例,通过与原有猜想或证明联系对比,提出新问题,通过分析解决新问题来加强或推翻猜想,在提出证明及构造反例的否定之否定过程中综合提升逻辑推理素养.
证明与反驳过程有利于学生正确认识数学证明.证明与反驳的过程实际是解决多个互相关联的问题的过程,一个个具体的问题通过任务设计嵌入到更大的探究活动中,服务于一个更上位的研究问题,这与单个的数学解题不同.学生在此过程可体会到反例发现的乐趣,反例与猜想证明的冲突,体会数学研究是怎样在矛盾中推进的,窥探真实数学研究的全过程,培养正确的数学观.
参考文献
[1][英]伊姆雷·拉卡托斯.证明与反驳——数学发现的逻辑[M].方刚,兰钊,译.上海:复旦大学出版社,2007:168.
[2][美]G·波利亚.数学与猜想[M].李心灿,王日爽,李志尧,译.北京:科学出版社,2001:序言.
[3]Marradez, R., Gutiérrez, ?. Proofs produced by secondary school students learning geometry in a dynamic computer environment[J]. Educational Studies in Mathematics, 2000, 44(1): 87-125.
[4] Komatsu, K., Jones, K. Task Design Principles for Heuristic Refutation in Dynamic Geometry Environments[J]. International Journal of Science and Mathematics Education, 2019, 17: 801- 824.
[5]Otten, S., Gilbertson, N. J., Males, L. M., Clark, D. L. The mathematical nature of reasoning and proving opportunities in geometry textbooks[J]. Mathematical Thinking and Learning, 2014, 16(1): 51-79.
[6]程靖,孫婷,鲍建生.我国八年级学生数学推理论证能力的调查研究[J].课程·教材·教法,2016,36(04):17-22.
作者简介 孙丹丹(1991—),女,山东济南人,博士;主要从事数学史与数学教育、信息技术与数学教育研究.
栗小妮(1984—),女,山西晋城人,博士;主要从事数学史与数学教育、数学教师知识研究.
中学数学杂志(初中版)2023年5期
