浅谈反例在初中数学教学中的应用
刘憎雨
(吉林省白山市长白朝鲜族自治县新房子镇中学 吉林白山 134408)
作为初中学科体系中的关键学科,数学包含的知识内容较多,且其中大部分晦涩抽象难懂,学生学习相对困难。近年来许多教育学者研究中提出在初中教学中引入反例,通过反例在教学中的应用,可取得较好效果,但如何具体应用、将反例应用到哪种类型问题中,仍是目前数学教学中需考虑的主要问题。因此,本文对初中数学教学中如何运用反例以及相关注意事项的探索有重要意义。
一、关于反例的基本解读
关于反例,一般可理解为符合命题条件但不符合结论的事实证明,或理解为可证明猜想有误的事实。本文从数学教学角度出发,其中所提及的反例符合多种特征,包括:①反例提出建立在正确的数学定理上;②被用于证明猜想是错误的;③具体实例,与数学猜想相关。部分研究中也对数学中的反例进行类型划分,有基本反例、关于充分必要条件的反正实例以及条件改变反证实例等,不同反例类型可用于不同的数学问题中。将反例引入到初中数学教学中,其作用表现在多方面,如通过反例可使师生间的互动增强,营造良好的教学环境。再如反例的应用,本身为一种数学解题技巧,对强化学生解题能力、锻炼解题思维、提高解题效率均有重要作用。而从教师角度,反例的运用也是改善教学手段的一种做法,对丰富数学教学手段有积极意义[1]。
二、初中数学教学中反例的具体应用
(一)反例在概念教学中的应用
初中数学教学中应用反例,首先体现在概念教学中,包括数学法则、数学定理以及数学公式等,学生接触这些概念时,多采取死记硬背方式,这种方式并不可取,取得的学习效果也微乎其微。在此背景下,引入反例,可弥补传统机械式记忆的不足。以三角形全等判定方法为例,其中涉及的知识点为“两个三角形两边及夹角分别对应相等,则两个三角形全等。”此时引入反例教学方法,将“夹角”理解为“一边的对角”,由学生对此进行判定,分析结果,老师指导下,学生能够发现“一边对角”下,获取的三角形并非为全等三角形。此时,学生便能理解该判定方法的内容,深刻理解“夹角”概念。整个反例应用下,学生在思考、判定中会进一步理解与掌握其中的定理概念。
(二)反例在辩证真假中的应用
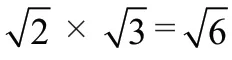
另外,反例应用下,也可帮助学生发现问题、解决问题。许多初中数学知识内容较为复杂,学生因为粗心大意未能发现自身错误,针对该情况,教师也可借助反例帮助学生及时找出问题所在,避免再犯同类错误。例如,关于相反数、绝对值,许多学生因为分不清可能引起解题错误情况。如给定例题,3的绝对值为-3,3 的相反数为-3;0 的绝对值为0,0 的相反数为-0,学生通过对两个例题的分辨,便能有效区分概念。同样,在实际解决问题中,利用反例也能帮助学生对知识点进行充分掌握,引导学生从中寻找到解题思路。
(三)反例在巩固知识中的应用
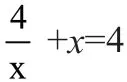
三、初中数学教学中反例应用注意事项
反例对于提升初中数学教学效果可发挥重要作用,但实际引入教学中有较多注意事项,如引入的反例应保证有目的性、针对性。若教学中盲目引入反例,对所有的命题知识都通过反例进行讲解,在占用课堂时间的同时,可能导致学生更加难分真假,起到反效果,所以引入的反例应保证目的性、针对性,尽可能用于重点、难点知识的学习上,服务教学[3]。
四、结束语
反例的应用是提高初中数学教学效果的关键。实际引入反例中,应正确认识反例应用的概念与作用,立足于当前初中数学教学实际,从概念教学、辩证真假以及巩固知识等多方面强化反例的应用。同时也需注意应用反例中保证其目的性与针对性,防止出现反例喧宾夺主的情况。这样才能保证反例的应用效果,实现数学教学质量与学生综合素养的提高。

